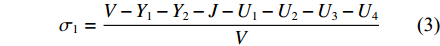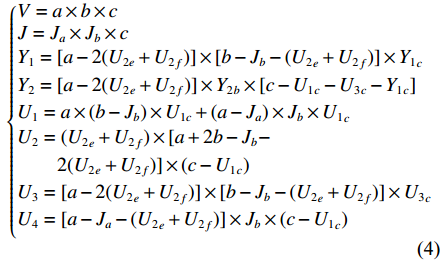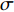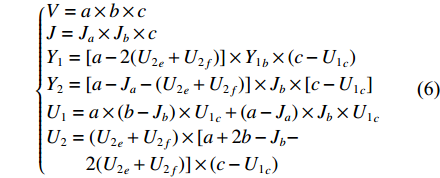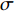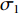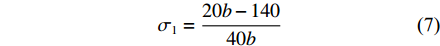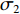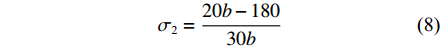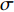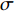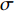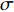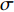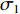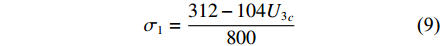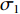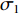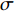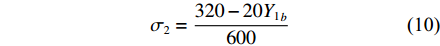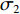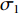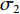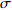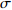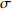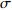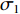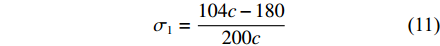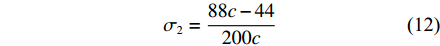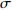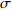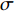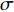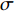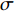Research on space utilization evaluation method of two typical ship warehouses
-
摘要:目的 根据舰船仓库的空间使用特点，研究舰船仓库空间利用率的评估方法。方法 提出一种舰船仓库空间利用率的通用评估公式，针对典型的行车仓库和叉车仓库予以细化完善，并进行算例分析。结果 结果显示，舰船仓库空间越大、设备装舰及使用需求越小，空间利用率就越高。结论 所得结论与实际结果一致，可有效指导工程实践，具备一定的研究价值。Abstract:Objectives According to the features of ship warehouse space utilization, an evaluation method for utilization rate of ship warehouse space is explored.Methods A general evaluation formula of space utilization rate is proposed, the definitions of two typical ship warehouses that cargo transfer therein is carried out by travelling crane and forktruck respectively are refined and improved, and examples of two typical ship warehouse space design are analyzed.Results The results show that the larger the ship warehouse space, the lower the equipment loading and use demand, and the higher the space utilization rate.Conclusions The results of this paper are consistent with actual engineering practice; as such, it has certain research value and can effectively guide future engineering practice in this field.
-
0. 引 言
舰船仓库是用于贮存食品、弹药、货物、维修备件等物资的功能舱室，提升舰船仓库的空间利用率可以提高舰船的持续作战能力，是大型水面舰船设计需要考虑的重要因素[1-3]。
目前，有关空间利用率的研究主要集中于舰船舱室布置方面。例如，刘明静和马运义[4]通过建立数学模型检验了结构强度和空间干涉，用以优化设备在矩形舱段的布置；李俊华等[5]采用模糊综合评价方法对指挥舱室布置方案进行了研究；胡耀等[6]采用层次分析法（analytic hierachy process，AHP）和满意度评价方法对舰船生活区舱室布置予以了评估；王宇等[7]采用引力搜索算法解决了船体多层甲板内的舱室布置问题；郭军[8]针对舰船水运装载空间单元化尺寸、托盘与装载空间实例，对空间利用率予以了分析。而在仓库的空间利用率方面，则主要集中在库存策略的运用和提高土地的利用2个方面。例如，易华等[9]针对季节性库存研究了一种混合仓储空间决策模型；韦尧兵等[10]建立了一种仓库空间决策模型，用于周期性库存条件下的主、副库容；王紫涵等[11]提出了一种新型立体停车库方案，用以提高城市土地的利用率。上述研究均针对的是陆上仓库的空间，无涉及舰船仓库空间利用率方面的研究，难以对舰船仓库方案优选提出有针对性的评估方法，因此需要根据舰船仓库的空间使用特点，研究舰船仓库空间利用率评估方法，以指导相关的研究和工程设计。
为此，本文将首先根据舰船仓库的基本组成，建立通用评估模型，然后针对舰船中典型的行车仓库和叉车仓库予以细化，提出相应的空间利用率评估公式，最后，根据算例得出这两类典型仓库在舰船平面设计、设备装舰设计和物资堆高方面的影响。
1. 通用评估公式
舰船仓库空间主要分为贮存空间、转运空间、不可用空间和升降空间4个部分。其中，贮存空间用于物资贮存，转运空间用于将贮存空间内的物资水平转运至升降空间，升降空间用于将物资垂直转运出仓库，不可用空间则用于仓库结构设计、管路设计、设备安装和人员通行等。对各空间的定义主要包括如下：
定义1：贮存空间
$ S=({S}_{1}，{S}_{2}，\cdots，{S}_{n}) $ ，其中Sn为可直接计算的单体贮存空间，n表示单个仓库舱内有n个单体贮存空间。定义2：转运空间
$ {Y}_{}=({Y}_{1}，{Y}_{2}，\cdots，{Y}_{m}) $ ，其中Ym为可直接计算的单体转运空间，m表示单个仓库舱内有m个单体转运空间。定义3：升降空间
$ {J}_{}=({J}_{1}，{J}_{2}，\cdots，{J}_{p}) $ ，其中Jp为单个升降空间，p表示单个仓库舱内有p个升降空间。定义4：不可用空间U=U1+U2+U3+U4，其中U1为结构和管路空间，U2为通行空间，U3为设备安装空间，U4为转运设备行程外空间。
定义5：仓库舱容V= Y+S+U+J。
根据上述定义，建立可评价仓库空间利用率评估公式如下：
$$ \sigma = \frac{S}{V} $$ (1) 式中，
$ \sigma $ 为空间利用率，指贮存空间在仓库内的空间占比，用于衡量仓库空间利用率。由于仓库舱容V、转运空间Y、升降空间J和不可用空间U均由设计方案直接给定，因此式（1）可变为：
$$ \sigma = \frac{{V - Y - J - U}}{V} $$ (2) 2. 典型的行车仓库有效贮存空间评估公式
行车仓库是采用行车来作为转运设备，主要由纵、横向移动梁和电动葫芦，以及纵、横向移动的驱动系统组成[12]。行车用于在仓库吊装转运对象，转运空间受行车运动原理的影响，其贮存空间的长度和宽度受结构、管路、转运空间、升降空间布置的影响，贮存空间的高度受物资堆垛高度的限制。在正常情况下，设计行车仓库时应将其贮存空间高度设计成与物资堆垛高度一致，以避免高度空间的浪费。
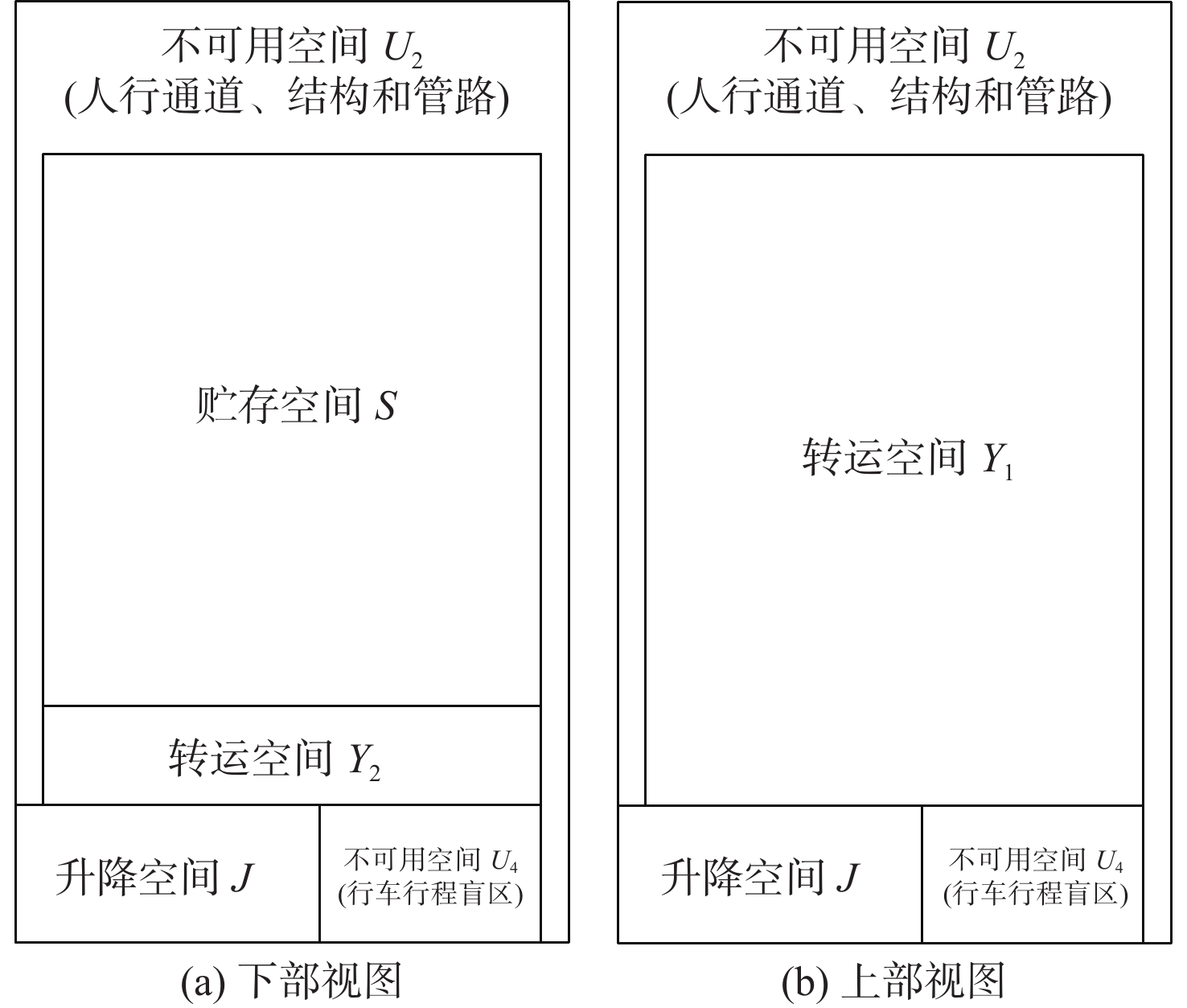
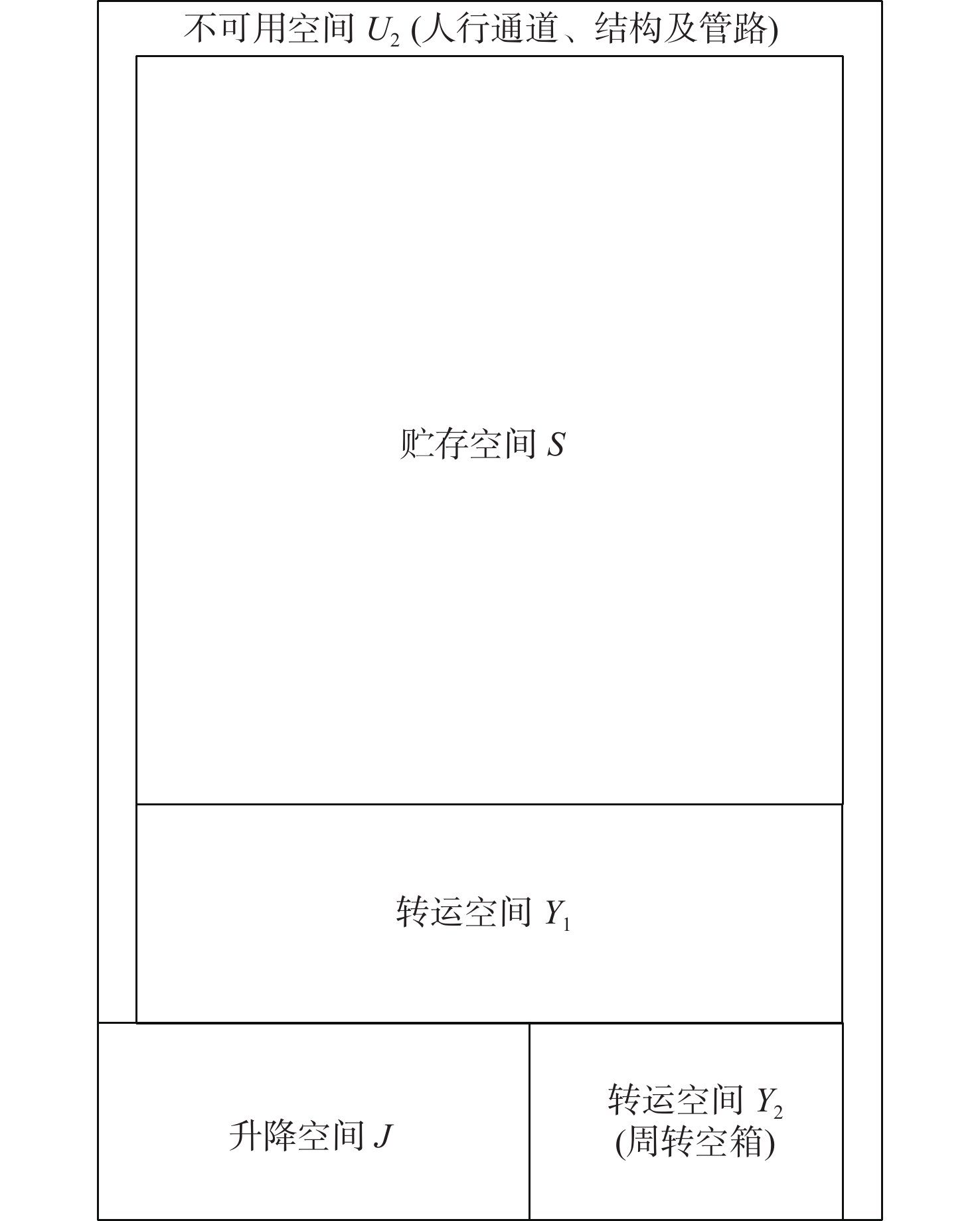
典型的行车仓库如图1和图2所示，其包含1个贮存空间、2个转运空间、1个升降空间和4个不可用空间。贮存空间用于堆垛贮存物资；转运空间包括上层水平移动空间Y1和下层吊放空间Y2；不可用空间包括上层结构和管路空间U1、下层人行通道、结构和管路空间U2、行车安装空间U3及行车行程盲区空间U4。
根据图1、图2和式（2），建立典型的行车仓库空间利用率评估公式如下：
$$ \sigma _1 = \frac{{V - {Y_1} - {Y_2} - J - {U_1} - {U_2} - {U_3} - {U_4}}}{V} $$ (3) 典型的行车仓库空间设计变量如表1所示。该空间是以图2所示的左右为长度方向，上下为宽度方向，以图1所示的上下为高度方向。
表 1 典型的行车仓库空间设计变量Table 1. Space design variables of typical warehouse handled by traveling crane空间 设计变量 变量符号 仓库舱容V 长/宽/高 a/b/c 升降空间J 长/宽 Ja /Jb 转运空间Y1 高 Y1c 转运空间Y2 宽 Y2b 不可用空间U1 高 U1c 不可用空间U2 人行通道宽度 U2e 不可用空间U2 结构和管路突出量 U2f 不可用空间U3 高 U3c $$ \left\{ \begin{aligned} & V = a \times b \times c \\& J = {J_a} \times {J_b} \times c \\& {Y_1} = [ {a - 2( {{U_{2e}} + {U_2}_f} )} ] \times [ {b - {J_b} - ( {{U_2}_e + {U_2}_f} )} ] \times {Y_1}_c \\& {Y_2} = [ {a - 2( {{U_2}_e + {U_2}_f} )} ] \times {Y_2}_b \times [ {c - {U_1}_c - {U_3}_c - {Y_1}_c} ] \\& {U_1} = a \times ( {b - {J_b}} ) \times {U_{1c}} + ( {a - {J_a}} ) \times {J_b} \times {U_1}_c \\& {U_2} = ( {{U_2}_e + {U_2}_f} ) \times [ a + 2b - {J_b} - \\&\qquad 2( {{U_2}_e + {U_2}_f} ) ] \times ( {c - {U_1}_c} ) \\& {U_3} = [ {a - 2( {{U_2}_e + {U_2}_f} )} ] \times [ {b - {J_b} - ( {{U_2}_e + {U_2}_f} )} ] \times {U_3}_c \\& {U_4} = [ {a - {J_a} - ( {{U_2}_e + {U_2}_f} )} ] \times {J_b} \times ( {c - {U_1}_c} ) \\& \end{aligned} \right. $$ (4) 合并式（3）和式（4），即可得到典型的行车仓库有效贮存空间占比
$ \sigma $ 相对于各个设计变量的函数关系式。3. 典型的叉车仓库有效贮存空间评估公式
叉车仓库是采用叉车来作为转运设备。叉车从地面叉取对象进行转运，其转运空间受叉车转运原理的影响，贮存空间的长度和宽度受结构、管路、转运空间及升降空间布置的影响，贮存空间的高度受物资堆垛高度的限制。在正常情况下，设计叉车仓库时应将其贮存空间高度设计成与物资堆垛高度一致，以避免高度空间的浪费。
典型的叉车仓库如图3和图4所示，其包含1个贮存空间、2个转运空间、1个升降空间和2个不可用空间。贮存空间用于堆垛贮存物资；转运空间包括叉车转运空间Y1和空箱转运空间Y2；不可用空间包括上层结构和管路空间U1，以及下层人行通道、结构和管路空间U2。
根据图3、图4和式（2），建立典型的叉车仓库空间利用率评估公式如下：
$$ \sigma _2 = \frac{{V - {Y_1} - {Y_2} - J - {U_1} - {U_2}}}{V} $$ (5) 典型的叉车仓库空间设计变量如表2所示。该空间是以图4所示的左右为长度方向，上下为宽度方向，以图3所示的上下为高度方向。
表 2 典型的叉车仓库空间设计变量Table 2. Space design variables of typical warehouse handled by forktruck空间 设计变量 变量符号 仓库舱容V 长/宽/高 a/b/c 升降空间J 长/宽 Ja /Jb 转运空间Y1 宽 Y1b 不可用空间U1 高 U1c 不可用空间U2 人行通道宽度 U2e 不可用空间U2 结构和管路突出量 U2f $$ \left\{ \begin{aligned} &V = a \times b \times c \\& J = {J_a} \times {J_b} \times c \\& {Y_1} = [ {a - 2( {{U_2}_e + {U_2}_f} )} ] \times {Y_1}_b \times ( {c - {U_1}_c} ) \\& {Y_2} = [ {a - {J_a} - ( {{U_2}_e + {U_2}_f} )} ] \times {J_b} \times [ {c - {U_1}_c} ] \\& {U_1} = a \times ( {b - {J_b}} ) \times {U_1}_c + ( {a - {J_a}} ) \times {J_b} \times {U_1}_c \\& {U_2} = ( {{U_2}_e + {U_2}_f} ) \times [ a + 2b - {J_b} -\\&\qquad 2( {{U_2}_e + {U_2}_f} ) ] \times ( {c - {U_1}_c} ) \end{aligned} \right. $$ (6) 合并式（5）和式（6），即可得到典型的叉车仓库有效贮存空间占比
$ \sigma $ 相对于各设计变量的函数关系式。4. 算例分析
根据表1和表2，设定典型的行车仓库和叉车仓库空间设计参数值分别如表3和表4所示（表中参数的单位：m）。仓库舱容的变量a和b一致，高度c由物资堆垛高度决定，本算例中，物资的堆垛高度为2.5 m；升降空间的Ja和Jb一致，不可用空间的U1c，U2e，U2f一致，转运空间参数因行车和叉车的转运特性不一样而不同。
表 3 典型的行车仓库空间设计参数Table 3. Space design parameters of typical warehouse handled by travelling crane空间 变量符号 参数值 仓库舱容V a/b/c 10/20/4 升降空间J Ja /Jb 5/3 转运空间Y1 Y1c 0.5 转运空间Y2 Y2b 3 不可用空间U1 U1c 0.5 不可用空间U2 U2e 0.5 不可用空间U2 U2f 0.5 不可用空间U3 U3c 0.5 表 4 典型的叉车仓库空间设计参数Table 4. Space design parameters of typical warehouse handled by forktruck空间 设计变量 参数值 仓库舱容V a/b/c 10/20/3 升降空间J Ja /Jb 5/3 转运空间Y1 Y1b 5 不可用空间U1 U1c 0.5 不可用空间U2 U2e 0.5 不可用空间U2 U2f 0.5 根据表3和表4所示设计参数，可分别得到典型的行车仓库和叉车仓库的有效贮存空间占比值分别为0.325和0.366，可见在相同的典型舱室面积情况下，叉车仓库的贮存空间利用率要高于行车仓库。
4.1 舱室平面设计分析
从仓库面积优化的角度出发，讨论舱室面积变化与有效贮存空间占比的关系。由于仓库在船长方向受制于船体分段的划分，船长方向设计变量a的可调范围较小，因此，仓库面积变化主要受船宽方向设计变量b的影响。
根据式（3）、式（4）以及表3，可以得到行车仓库有效贮存空间占比
$ {\sigma _1} $ 与设计变量b之间的关系式为：$$ {\sigma _1} = \frac{{20b - 140}}{{40b}} $$ (7) 根据式（5）、式（6）以及表4，可以得到叉车仓库有效贮存空间占比
$ {\sigma _2} $ 与设计变量b之间的关系式为：$$ {\sigma _2} = \frac{{20b - 180}}{{30b}} $$ (8) 根据式（7）和式（8），可以计算出行车仓库和叉车仓库σ的理论极限值分别为0.44和0.66。由于舰船的宽度不可能无限大，参考舰船设计水线宽[13]，设定b的取值区间为[10，30]。行车仓库与叉车仓库
$ {\sigma _{}} $ 值的变化曲线如图5所示。![]()
图 5 两种典型车仓库的$ {\sigma _{}} $ 值随设计变量b的变化曲线Figure 5. Variation curves of value-$ {\sigma _{}} $ with design variable-b for two typical warehouses由图5可以看出，行车仓库和叉车仓库的
$ {\sigma _{}} $ 值是随设计变量b值的增大而不断增大的。当b=15 m时，两类仓库的$ {\sigma _{}} $ 值相当；当b<15 m时，行车仓库的$ {\sigma _{}} $ 值较大；当b>15 m时，叉车仓库的$ {\sigma _{}} $ 值较大。代入a=10 m的前提条件后，在表3、表4给定其他设计参数的条件下，当仓库面积小于150 m2时，行车仓库内的空间利用率较大，当仓库面积大于150 m2时，叉车仓库内的空间利用率较大。
4.2 设备装舰设计分析
从行车设计优化的角度出发，分析行车安装高度与仓库有效贮存空间间的关系。根据式（3）、式（4）和表3，可以得到行车仓库有效贮存空间占比
$ {\sigma _1} $ 与设计变量U3c间的关系式为：$$ {\sigma _1} = \frac{{312 - 104{U_3}_c}}{{800}} $$ (9) 考虑到行车移动梁、电动葫芦、嵌入结构安装等改进形式，可适当减小U3c的取值。由计算式（9）可知，U3c每降低0.1 m，
$ {\sigma _1} $ 的值就增加0.013，当U3c=0 m时，$ {\sigma _1} $ 达到极限值0.39，但还无法达到典型叉车仓库的$ \sigma $ 值。从叉车设计优化的角度出发，分析叉车转运空间减小与仓库有效贮存空间间的关系。根据式（5）、式（6）和表4，可以得到叉车仓库有效贮存空间占比
$ {\sigma _2} $ 与设计变量Y1b间的关系式为：$$ {\sigma _2} = \frac{{320 - 20{Y_1}_b}}{{600}} $$ (10) 考虑到叉车会减小转弯半径或不在内仓库转运，可以适当减小Y1b的取值。由计算式（10）可知，Y1b每减小1 m，
$ {\sigma _2} $ 的值就增加0.033，当Y1b=0 m时，$ {\sigma _2} $ 达到极限值0.533。综合式（9）和式（10）可以发现，当叉车仓库的Y1b>4 m时，只有减小U3c后，行车仓库的空间利用率
$ {\sigma _1} $ 才有可能大于叉车仓库的空间利用率$ {\sigma _2} $ ，如表5和表6所示。表 5 U3c取值不同时的$ {\sigma _{}} $ 值Table 5. Value-$ {\sigma _{}} $ varying with value-U3cU3c $ {\sigma _1} $ 0 0.390 0.1 0.377 0.2 0.364 0.3 0.351 0.4 0.338 0.5 0.325 0.6 0.312 0.7 0.299 0.8 0.286 0.9 0.273 1.0 0.260 表 6 Y1b取值不同时的$ {\sigma _{}} $ 值Table 6. Value-$ {\sigma _{}} $ varying with value-Y1bY1b $ {\sigma _2} $ 0 0.533 1 0.500 2 0.467 3 0.433 4 0.400 5 0.367 6 0.333 7 0.300 8 0.267 9 0.233 10 0.200 4.3 物资堆垛高度影响分析
物资堆垛高度直接影响仓库层高的设计，从优化贮存对象的角度，分析堆垛高度与仓库有效贮存空间之间的关系。
根据式（3）、式（4）和表3，可以得到行车仓库有效贮存空间占比
$ {\sigma _1} $ 与设计变量c间的关系式为：$$ {\sigma _1} = \frac{{104c - 180}}{{200c}} $$ (11) 根据式（5）、式（6）和表4，可得到叉车仓库有效贮存空间占比
$ {\sigma _2} $ 与设计变量c间的关系式为：$$ {\sigma _2} = \frac{{88c - 44}}{{200c}} $$ (12) 根据式（11）和式（12），可以得到典型行车仓库和叉车仓库有效贮存空间占比
$ {\sigma _{}} $ 相对于设计变量c的变化曲线如图6所示。![]()
图 6 两种典型仓库的$ {\sigma _{}} $ 值随设计变量c的变化曲线Figure 6. Variation curves of value-$ {\sigma _{}} $ with design variable-c for two typical warehouses由图6可以看出，行车仓库和叉车仓库的
$ {\sigma _{}} $ 取值是随设计变量c的增大不断增大的。当c=9 m时，这两类仓库的$ {\sigma _{}} $ 值相当；当c<9 m时，叉车仓库的$ {\sigma _{}} $ 值较大；当c>9 m时，行车仓库的$ {\sigma _{}} $ 值较大。设计变量c的取值是根据物资堆垛能力确定的，当物资具备更高堆垛能力时，对行车仓库空间利用率的提升更有利。然而，考虑到舰船的摇摆特性，堆垛越高，其倾倒风险越大，故堆垛高度一般增量较小。4. 结 语
仓库空间利用率是衡量舰船设计的重要指标，本文基于舰船仓库的特点，建立了通用评估公式，并针对典型的行车仓库和叉车仓库细化提出了相应的空间利用率评估公式，然后，通过算例，分析了舰船上这两类典型仓库在平面设计、设备装舰设计、物资堆垛高度影响方面的关联关系。研究表明，仓库空间越大，设备装舰及使用需求越小，空间利用率越高，其中行车更适应于在小面积、大层高的仓库中使用，而叉车则更适应于大面积、小层高的仓库中使用。
然而，本文只针对典型的行车仓库和叉车仓库的贮存空间进行了讨论，未综合考虑出入库的效率。因此，后续将在本文方法的基础上，结合物资出入库的流程进一步分析出入库的效率，并扩大研究范围。
-
![]()
图 5 两种典型车仓库的
$ {\sigma _{}} $ 值随设计变量b的变化曲线Figure 5. Variation curves of value-
$ {\sigma _{}} $ with design variable-b for two typical warehouses![]()
图 6 两种典型仓库的
$ {\sigma _{}} $ 值随设计变量c的变化曲线Figure 6. Variation curves of value-
$ {\sigma _{}} $ with design variable-c for two typical warehouses表 1 典型的行车仓库空间设计变量
Table 1 Space design variables of typical warehouse handled by traveling crane
空间 设计变量 变量符号 仓库舱容V 长/宽/高 a/b/c 升降空间J 长/宽 Ja /Jb 转运空间Y1 高 Y1c 转运空间Y2 宽 Y2b 不可用空间U1 高 U1c 不可用空间U2 人行通道宽度 U2e 不可用空间U2 结构和管路突出量 U2f 不可用空间U3 高 U3c 
下载: 导出CSV
表 2 典型的叉车仓库空间设计变量
Table 2 Space design variables of typical warehouse handled by forktruck
空间 设计变量 变量符号 仓库舱容V 长/宽/高 a/b/c 升降空间J 长/宽 Ja /Jb 转运空间Y1 宽 Y1b 不可用空间U1 高 U1c 不可用空间U2 人行通道宽度 U2e 不可用空间U2 结构和管路突出量 U2f
下载: 导出CSV
表 3 典型的行车仓库空间设计参数
Table 3 Space design parameters of typical warehouse handled by travelling crane
空间 变量符号 参数值 仓库舱容V a/b/c 10/20/4 升降空间J Ja /Jb 5/3 转运空间Y1 Y1c 0.5 转运空间Y2 Y2b 3 不可用空间U1 U1c 0.5 不可用空间U2 U2e 0.5 不可用空间U2 U2f 0.5 不可用空间U3 U3c 0.5
下载: 导出CSV
表 4 典型的叉车仓库空间设计参数
Table 4 Space design parameters of typical warehouse handled by forktruck
空间 设计变量 参数值 仓库舱容V a/b/c 10/20/3 升降空间J Ja /Jb 5/3 转运空间Y1 Y1b 5 不可用空间U1 U1c 0.5 不可用空间U2 U2e 0.5 不可用空间U2 U2f 0.5
下载: 导出CSV
表 5 U3c取值不同时的
$ {\sigma _{}} $ 值Table 5 Value-
$ {\sigma _{}} $ varying with value-U3cU3c $ {\sigma _1} $ 0 0.390 0.1 0.377 0.2 0.364 0.3 0.351 0.4 0.338 0.5 0.325 0.6 0.312 0.7 0.299 0.8 0.286 0.9 0.273 1.0 0.260
下载: 导出CSV
表 6 Y1b取值不同时的
$ {\sigma _{}} $ 值Table 6 Value-
$ {\sigma _{}} $ varying with value-Y1bY1b $ {\sigma _2} $ 0 0.533 1 0.500 2 0.467 3 0.433 4 0.400 5 0.367 6 0.333 7 0.300 8 0.267 9 0.233 10 0.200
下载: 导出CSV
-
[1] 于辉, 王治国, 李晶晶, 等. 基于0-1整数规划的舰船内集装物资存放方法[J]. 中国舰船研究, 2015, 10(3): 121–126. doi: 10.3969/j.issn.1673-3185.2015.03.020 YU H, WANG Z G, LI J J, et al. The method of integrated materials placement on ships with 0/1 programming[J]. Chinese Journal of Ship Research, 2015, 10(3): 121–126 (in Chinese). doi: 10.3969/j.issn.1673-3185.2015.03.020
[2] 史文强, 李彦庆, 陈练. 航母的航空弹药贮运作业解析[J]. 舰船科学技术, 2013, 35(6): 136–141. doi: 10.3404/j.issn.1672-7649.2013.06.030 SHI W Q, LI Y Q, CHEN L. Analysis for the ordnance handling process aboard aircraft carrier[J]. Ship Science and Technology, 2013, 35(6): 136–141 (in Chinese). doi: 10.3404/j.issn.1672-7649.2013.06.030
[3] 李红军. 国外综合补给舰的发展现状与特点[J]. 现代军事, 2015(5): 63–65. LI H J. Development status and characteristics of foreign integrated supply ships[J]. Conmilit, 2015(5): 63–65 (in Chinese).
[4] 刘明静, 马运义. 舱室布置设计优化方法研究[C]//第四届全国船舶与海洋工程学术会议论文集. 镇江: 中国造船工程学会, 2009: 297–300. LIU M J, MA Y Y. Optimization on cabin layout[C]//Proceedings of the 4th National Conference on Ship and Ocean Engineering. Zhenjiang: The Chinese Society of Naval Architects and Marine Engineer, 2009: 297–300 (in Chinese).
[5] 李俊华, 陈宾康, 应文烨, 等. 船舶舱室布置方案的模糊综合评价[J]. 中国造船, 2000, 41(4): 22–27. doi: 10.3969/j.issn.1000-4882.2000.04.004 LI J H, CHEN B K, YING W Y, et al. Fuzzy comprehensive evaluation for vessel compartment layout[J]. Shipbuilding of China, 2000, 41(4): 22–27 (in Chinese). doi: 10.3969/j.issn.1000-4882.2000.04.004
[6] 胡耀, 姜治芳, 熊治国, 等. 基于AHP和满意度评价的舰船生活区舱室布置评估[J]. 舰船科学技术, 2013, 35(9): 38–43. doi: 10.3404/j.issn.1672-7649.2013.09.006 HU Y, JIANG Z F, XIONG Z G, et al. Study of warship living district cabin layout assessment based on AHP and satisfaction evaluation[J]. Ship Science and Technology, 2013, 35(9): 38–43 (in Chinese). doi: 10.3404/j.issn.1672-7649.2013.09.006
[7] 王宇, 黄胜, 廖全蜜, 等. 基于引力搜索算法的船舶舱室布置方法[J]. 上海交通大学学报, 2016, 50(1): 131–139. WANG Y, HUANG S, LIAO Q M, et al. A method for ship compartment layout design based on gravitational search algorithm[J]. Journal of Shanghai Jiao Tong University, 2016, 50(1): 131–139 (in Chinese).
[8] 郭军. 集装化运输系统优化设计之四舰船装载空间利用率分析[J]. 中国包装工业, 2000(3): 41–44. GUO J. Optimal design of containerized transportation system IV analysis of ship loading space utilization[J]. China Packaging Industry, 2000(3): 41–44 (in Chinese).
[9] 易华, 张文杰. 季节性库存条件下混合仓储空间的决策模型研究[J]. 物流技术, 2006(5): 32–34. doi: 10.3969/j.issn.1005-152X.2006.05.012 YI H, ZHANG W J. On decision model of hybrid warehousing space under the condition of seasonal inventory[J]. Logistics Technology, 2006(5): 32–34 (in Chinese). doi: 10.3969/j.issn.1005-152X.2006.05.012
[10] 韦尧兵, 张云鹤, 武新柱, 等. 周期性库存条件下仓储空间的决策模型研究[J]. 科学技术与工程, 2007, 7(14): 3623–3625. doi: 10.3969/j.issn.1671-1815.2007.14.071 WEI Y B, ZHANG Y H, WU X Z, et al. On decision model of warehousing space under the condition of periodicity inventory[J]. Science Technology and Engineering, 2007, 7(14): 3623–3625 (in Chinese). doi: 10.3969/j.issn.1671-1815.2007.14.071
[11] 王紫涵, 陈晶晶, 周腾, 等. 面向提高空间利用率的新型立体停车库研究[J]. 科教导刊, 2018(35): 36–38. WANG Z H, CHEN J J, ZHOU T, et al. A new type of stereoscopic parking garage for improving the utilization ratio of space[J]. The Guide of Science & Education, 2018(35): 36–38 (in Chinese).
[12] 智广信, 瞿荣泽, 薛国良. 超大型集装箱船机舱行车设计安装研究[J]. 中国特种设备安全, 2019, 35(7): 13–15. doi: 10.3969/j.issn.1673-257X.2019.07.004 ZHI G X, QU R Z, XUE G L. Research on design and installation of super large container ship cabin[J]. China Special Equipment Safety, 2019, 35(7): 13–15 (in Chinese). doi: 10.3969/j.issn.1673-257X.2019.07.004
[13] 屈俊飞. 大型水面舰船总体性能综合评估[J]. 军事交通学院学报, 2018, 20(9): 45–49. QU J F. Comprehensive evaluation of overall performance of large surface ship[J]. Journal of Military Transportation University, 2018, 20(9): 45–49 (in Chinese).
计量
- 文章访问数: 431
- HTML全文浏览量: 281
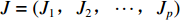
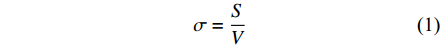
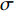
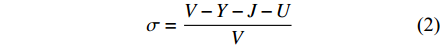
- PDF下载量: 10
