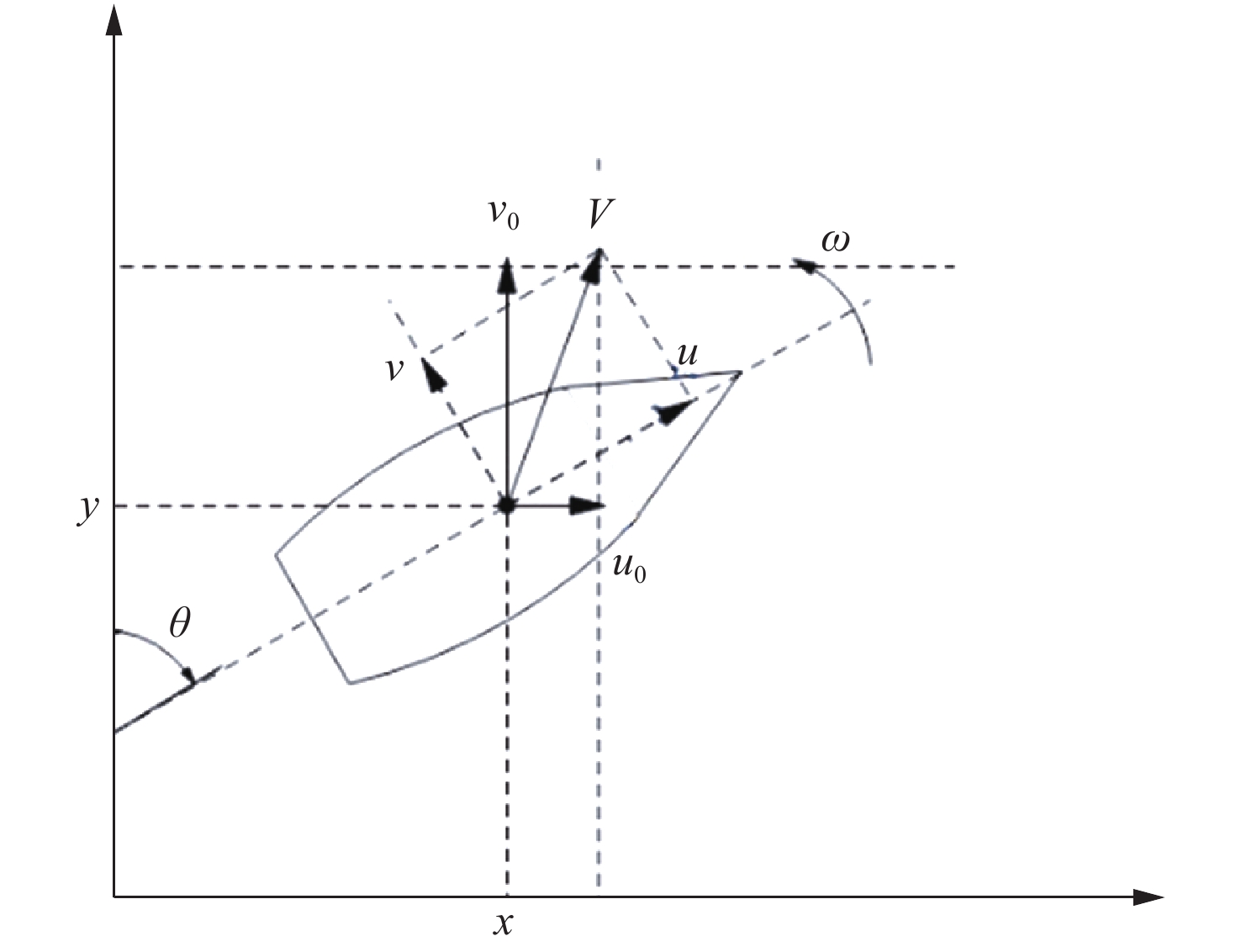
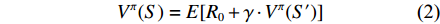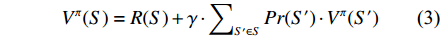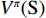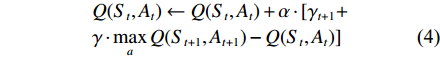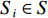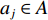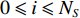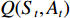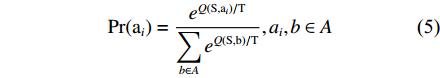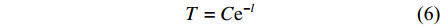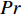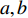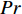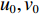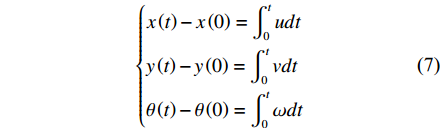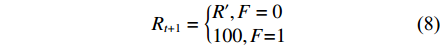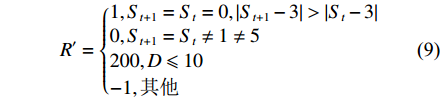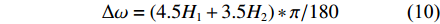A Real-time Q-Learning Algorithm for Unmanned Surface Vehicle Target Tracking
-
摘要: 针对无人艇运动规划中的目标跟踪问题，研究增强学习方法在无人艇目标跟踪控制中的应用。通过分析增强学习的模型和特点，提出改进的实时Q学习算法。设计适用于无人艇目标跟踪问题的Q学习算法模型框架，包括行为空间、状态空间、回报函数以及强化学习策略。在固定和不确定的环境中，设计离线和在线测试场景，对自学习算法和控制效果进行分析研究。结果表明，所设计的Q学习算法模型具有自学习的能力，可以自主的进化行为策略，最大化回报函数，实现实时目标跟踪的效果。可以为增强无人艇控制系统的自学习能力提供研究基础。Abstract: On the background of motion planning problem, the application of enforcement learning method in unmanned surface vehicle target tracking is studied in this paper. The enforcement learning process and Q-learning model is analyzed, the improved algorithm is presented. The Q-learning algorithm framework which is suit for target tracking problem is implemented. This framework includes action space, state space, reward function, and reinforcement learning strategy. After that, based on the offline and online test scenes in certain and uncertain environment, the self-learning algorithm and control effectiveness are analyzed. The result shows that Q-learning algorithm framework has the ability of self-learning, could autonomous evolve action strategy, maximize reward function, and achieve real-time target tracking effectiveness. This work provides a research basis for increasing the self-learning ability of unmanned surface vehicle control system.
-
1. 引 言
在无人艇（unmanned surface vehicle，USV）运动规划与控制领域，设计性能良好的控制系统，进一步提高系统自主性和智能性是一项长期的挑战[1-2]，具有重要的意义。
目前采用的控制方法主要有经典控制论方法和一些智能控制方法[3-4]，其中经典控制论方法依赖控制对象的精确模型，在USV船体运动建模和环境建模中会遇到较大的困难。常规智能控制方法可以不依赖于对象精确模型，提高了控制系统的鲁棒性，但控制结构和控制参数相对固定，缺乏自学习和自调整的能力。另一方面，增强学习是人工智能的一个重要分支[5-7]，增强学习方法从现有状态出发，通过学习算法不断优化行为策略，使控制系统成为自学习自进化系统，从而进一步提高控制系统的智能性。
本文将以提高USV的自主目标跟踪能力为目标，采用增强学习的方法，提出一种改进的实时Q学习算法，建立控制系统Q学习算法模型框架，设计相应的强化学习策略，为USV在执行已有策略和探索新行为策略之间做出合理的选择。并进一步设计试验场景，开展计算分析，对自学习算法和控制效果进行分析研究，对结果进行讨论总结。
2. 实时Q学习算法
2.1 增强学习过程与Q学习
增强学习通过与动态环境的交互来学习行为策略，并得到回报[8-9]。增强学习问题框架可以由马尔可夫决策过程（Markov decision process，MDP）模型来描述，其基本构成如式（1）所示。
({S},{A},Pr,γ,{R}) (1) 式中：{S}为一组离散的状态序列；{A}为一组离散的行为序列；Pr为状态转移概率函数；γ为折扣因子；{R}为回报值。这个MDP模型的动态变化过程如图1所示。
系统的初始状态为S0，采取了决策行为A0后，系统以概率Pr(S0,A0)转变为状态S1，同时得到回报值R1。E为数学期望符号。系统变化到状态S1后，状态转移过程继续进行，可以得到一个状态序列{S}，行为序列{A}，回报值序列{R}。
定义预期收益的值函数如式（2）所示，下一时刻的值函数通过折扣因子γ对上一时刻的值函数进行效果递推。
Vπ(S)=E[R0+γ⋅Vπ(S′)] (2) 算法的目标是在当前状态下找到最优的行动策略，以最大化预期收益，即未来所有的回报。在式（2）中加入状态转移概率后，表达形式可以转换成式（3）
Vπ(S)=R(S)+γ⋅∑S′∈SPr(S′)⋅Vπ(S′) (3) 式中：
Vπ(S) 为在选择一个行为策略π后，未来可获得的所有回报值的预期收益值函数；S’为下一个状态。最优策略是一个函数π(S,A)，它将状态集映射到行为集。在USV目标跟踪任务中，最优策略指采取航向航速变化的最佳行为策略到达目标。在增强学习中，系统只知道上一时刻和当前的状态，以及基于先前行为的回报值。通过这些信息学习到状态与动作的映射，最大限度地提高未来的总回报值。
在求解最优行为策略的过程中，出现了多种算法模型，包括动态规划、蒙特卡洛方法、时序差分（time-differential，TD）方法等。Q学习属于TD算法的一种，是增强学习算法的一个重要突破，最早由Watkins提出[10-12]。
与采用状态值函数作为优化目标的其它算法不同，Q学习算法采用动作值函数作为优化目标，用来评估在特定状态下采取行动的利弊。Q学习算法可以将学习策略与控制策略分开。可以把Q看作是一张表格，表中的每一行都是一个状态，每一列代表一个动作。在控制模式时，算法将根据当前的状态找到相应的行，然后比较每一列概率值的大小（动作），选择概率值较大的动作作为当前状态下应采取的行为。而在学习模式时，算法可以按照一定的规则在所有可能的行为中进行探索和学习。
2.2 Q学习算法及其改进
在具体的Q学习算法中，采用Belman方程更新Q表中的动作值函数
Q(St,At) ，如式（4）所示：Q(St,At)←Q(St,At)+α⋅[γt+1+γ⋅max (4) Q学习算法使用有限离散状态组
{S_i} \in S 和动作组{a_j} \in A ，其中0 \leqslant i \leqslant {N_S} ，0 \leqslant j \leqslant {N_A} ，NS和NA分别是离散的状态空间和动作空间的维度。Q({S_t},{A_t}) 是在t时刻，系统处于状态St，采取行为at后，获得的动作回报Q值。γ用于调整未来回报对Q值更新的影响。当它很小的时候，算法只会增加当前回报的权重。当γ变大时，未来的回报加权会更重。学习率因子α控制着学习步长，意味着会有多少之前的训练效果被保留。Q表的具体学习过程如图2中的伪代码所示，其中“GetAction”即“获取行为”指学习策略，它根据“当前状态”选择“行为”。
学习策略是Q学习算法的关键问题，常规的学习策略可以与控制策略一样，在所有的可能行为中，按照固定的概率分布，直接选择概率最大的作为下一步应采取的动作。但这种方法可能会陷入局部最优，无法选择出短期内看起来次优，长期来看可能更好的动作，同时还会增加算法的收敛时间。
本文设计了一种改进的学习策略，其原理是根据学习次数和学习效果的变化来相应调整学习策略中的动作选择概率，即自动调整在解空间中的搜索策略。具体的方法是：将动作选择概率定义为估计值T的梯度函数，将所有动作根据其T值赋以不同的概率，T随学习次数的变化而变化。
所设计的改进学习策略如式（5）和式（6）所示：
\Pr ({{\rm{a}}_i}) = \frac{{{e^{Q({\rm{S}},{{\rm{a}}_i})/{\rm{T}}}}}}{{\displaystyle\sum\limits_{b \in A} {{e^{Q({\rm{S}},{\rm{b}})/{\rm{T}}}}} }},{a_i},b \in A (5) T = C{{\rm{e}}^{ - l}} (6) 式中：
Pr 为状态转移概率函数；e为自然常数；T为估计值参数；A为动作集；a,b 为动作集中的动作；C为初始化的系数；l为学习次数。式（5）中，
Pr 根据动作对应的Q和T来确定概率。Q值大的动作被选择的概率也更大，同时Pr也随T动态变化，当T较大时，选择任一动作的概率大致均等，从而有利于在解空间中概率性地跳出局部最优，学习探索更多的新行为策略；当T较小时，Pr随着其最大Q值的增加而增加，倾向于使用已有的行为经验。式（6）中，T随着l的增加而减小。随着学习的深入，行为策略的探索成分随之减小，避免了由于大量探索而造成的算法性能下降，可加快Q值的收敛。
3. USV目标跟踪Q学习算法
USV的基本运动学模型如图3所示，在后续的计算分析中用于描述USV的运动规律。其目标跟踪控制模型采用上节中提出的改进Q学习算法模型。
图中：
x,y,\theta ,V 分别为USV的位置、航向、航速，u,v,\omega 分别为USV在随动坐标系下的速度分量及角速度，{u_0},{v_0} 分别为USV在惯性坐标系下的速度分量。则USV在离散时间下的运动学公式为{\left\{ \begin{aligned} & {x\left( t \right) - x\left( 0 \right) = \int_0^t {udt} } \\ & {y\left( t \right) - y\left( 0 \right) = \int_0^t {vdt} } \\ & {\theta \left( t \right) - \theta \left( 0 \right) = \int_0^t {\omega dt} } \end{aligned} \right.} (7) \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {u_0} \\ {v_0} \\ \omega \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos\theta }&{ - \sin\theta }&0 \\ {\sin\theta }&{\cos\theta }&0 \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} u \\ v \\ \omega \end{array}} \right]} \end{array} (8) 3.1 行为空间
在Q学习中，将行为离散化为若干种，构成行为空间，针对本文所研究的问题，为了降低状态−行为映射的数量和学习次数，只选择正向行为。将USV的行为细化为3种：左转弯、直行、右转弯。行为参数的线速度和角速度的设计如表1所示。所设计的角速度对应于设计的线性速度，满足公式V＝ωr的最大可实现角速度，其中r是USV的最小曲率半径。
表 1 USV行为参数Table 1. Chosen USV action velocities行为 速度(kn) 角速度(rad/s) 左转弯 10 0.26 向前直行 10 0 右转弯 10 −0.26 3.2 状态空间
USV设计有2个传感器，其中传感器1是方向传感器，传感器2是位置传感器。方向传感器用于估计目标相对于USV的方向。位置传感器用于在二维环境地图中定位USV。如图4所示，将方向离散为8个状态，如果方向落在指定的边界内，则根据相应的区域得到离散方向。
因此，状态空间的维数为8，行为空间的维数为3，共24个状态-行为对。状态数量相对少使得USV能快速学习。
3.3 回报函数
式（7）~式（9）是回报函数的计算模型。回报函数使用当前和下一个状态，参数F标志着USV是否碰到障碍物或边界。
D = \sqrt {{{({x_t} - {x_u})}^2} + {{({y_t} - {y_u})}^2}} (7) {R_{t + 1}} = \left\{ { \begin{aligned} & {R',F = {\rm{0}}}\\& {100,F{\rm{ = }}1} \end{aligned}} \right. (8) R' = \left\{ { \begin{aligned} & {1,{S_{t + 1}} = {S_t} = 0,\left| {{S_{t + 1}} - 3} \right| > \left| {{S_t} - 3} \right|}\\& {0,{S_{t + 1}} = {S_t} \ne 1 \ne 5}\\& {200,D \leqslant 10}\\& { - 1,{\text{其他}}} \end{aligned}} \right. (9) 式（7）利用传感器获得的USV位置和目标位置计算距离D。式（8）中给出了USV与障碍物或边界碰撞的回报为−100，这是一个较大的惩罚值。根据等式（9）中的条件给出相应的回报值。当与目标的航向误差减小，目标持续在USV前面时，回报值给予正强化。当与目标的航向误差增大或目标一直在USV后面时，给出了负强化。
具体地，当前状态和下一时刻状态都是前中心状态时给出1的回报值，同时表示目标在USV前面；当USV的航向误差减小，其方向状态变得接近前中心状态时，也给出1的回报值。
当方向状态不改变，且目标不直接在USV的前方或后方时，USV回报值为0；当航向误差增大或目标在USV后面时，给予−1的回报值；如果USV成功进入目标圆以内时，给予200的较大回报值，鼓励USV快速抵达目标。
4. 计算分析
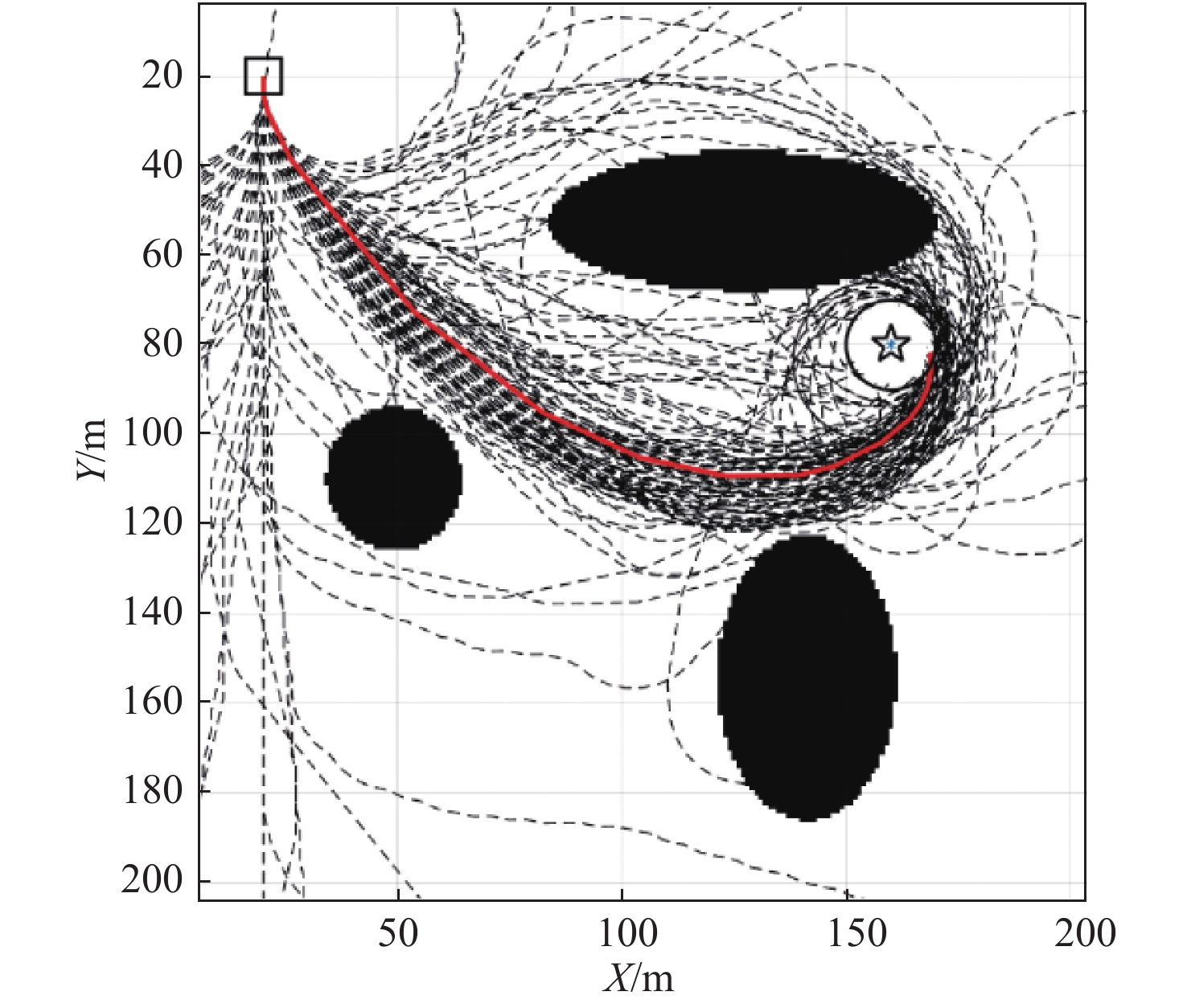
在计算场景设计中，USV的活动区域为200米×200米的方形水域，设置3个岛屿状障碍物，如图5所示。黑块是障碍物和边界，在地图中已经被栅格化，正方形是USV的起始点，五角星代表目标，它由到达圆所包围。学习过程中，如果USV进入目标圆区域，遇到障碍物，或者碰到边界，则进入学习终止状态，重新开始下一次学习。USV被重置到下一次学习阶段的初始位置，初始状态随机。
在计算分析中对于行为选择策略及其参数，令系数C=0.9，学习率α=0.1，折扣因子γ=0.9，Q表中的元素从−0.1到0.1的随机值初始化。
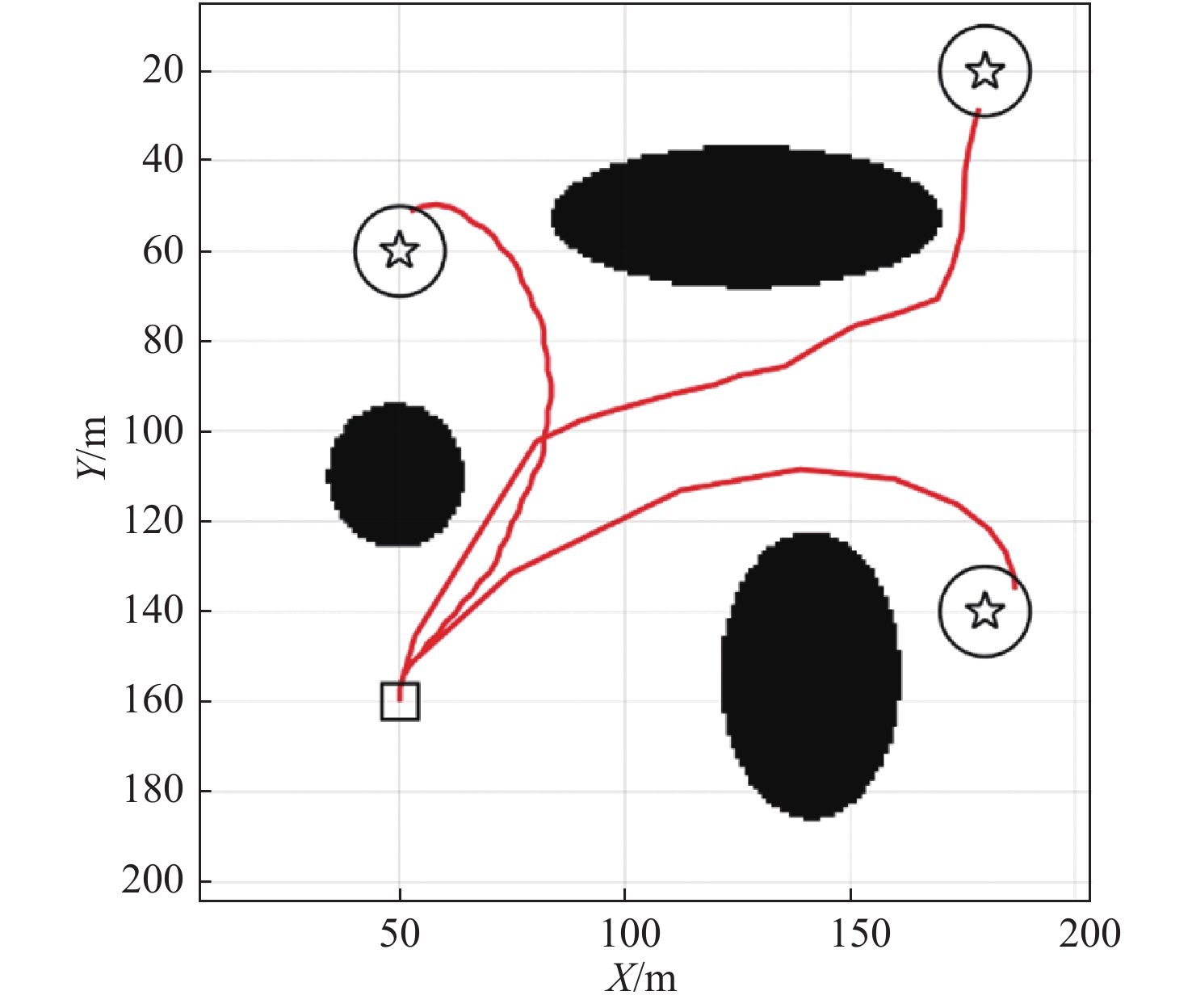
此外，考虑到工作环境中风、浪、流对USV运动的影响，采用经验公式模拟USV在航行时的扰动。风、浪、流的一般正态分布的随机扰动作用于角速度ω，如式（10）所示。
\Delta \omega = (4.5{H_1} + 3.5{H_2})*{\rm{\pi }}/180 (10) 式中，H1和H2是2个由正态分布N[0,1]获得的随机变量。
4.1 在固定环境中离线学习
为了验证Q学习算法的有效性，先进行离线学习的计算分析，完成足够的离线学习次数后，再开展实际的目标跟踪任务。考虑运行环境为固定环境，即目标位置固定、活动区域和障碍物位置不变。图5所示是200次学习过程的计算结果，黑色细虚线是每次的学习路径。红色轨迹是最终的最佳路径。
在图5中可以看出，在学习了一些错误的经验之后，USV成功地选择了最有效和最安全的运动路径。它表明经过学习迭代，Q表获得了收敛的结果。同时，可以发现在顶部障碍物上方有一些学习路径，由于太接近障碍物，以及碰到障碍物的惩罚值较大，频繁的撞上障碍物减少了这些冒险行为的出现概率，最终USV在学习过程中自动放弃了这些路径。
图6所示是200次Q学习过程中，终止时间的变化，可以看出，在大约51次学习之后，终止时间就接近于收敛线。
在最初的几次学习中，USV在碰撞到边界后就终止了学习过程。之后USV学会避开边界和障碍物随机学习，这时的运动路径也是随机变化的，直到第51次时，USV第1次抵达了目标圆区域发现目标，获得了200的回报值，巨大的正向激励使USV记住了成功的决策过程和行为决策矩阵，使得后续学习中终止时间急剧下降。余下的时间，USV通过行动随机选择策略π尽可能多地尝试一个更有效的路径。根据式（5）和式（6），对收敛做出更早的判断可以提前结束探索，这是缩短学习次数的一个可行方法。
4.2 在不确定环境中在线学习
进一步的，计算分析USV在开展目标跟踪任务的同时，进行在线学习持续更新Q表的情况。为了验证Q表的收敛性和消除环境扰动的影响，设计了3种不确定环境中的目标跟踪在线学习的场景：
1）不同起始点和初始方向，相同目标。
2）相同起始点和初始方向，不同目标。
3）以给定速度移动的运动目标。
离线学习计算中，200次学习的计算时间为350 ms，在线学习中，设计USV在运动的同时按照学习算法进行学习，使用500 ms的时间间隔来更新Q表。该方法可以满足USV在线学习的要求。以上3种在线学习场景的计算结果分别如图7~图9所示。
![]()
图 7 不同起始点和初始方向，相同目标的计算结果Figure 7. Results of different starting points and initial directions with a same target![]()
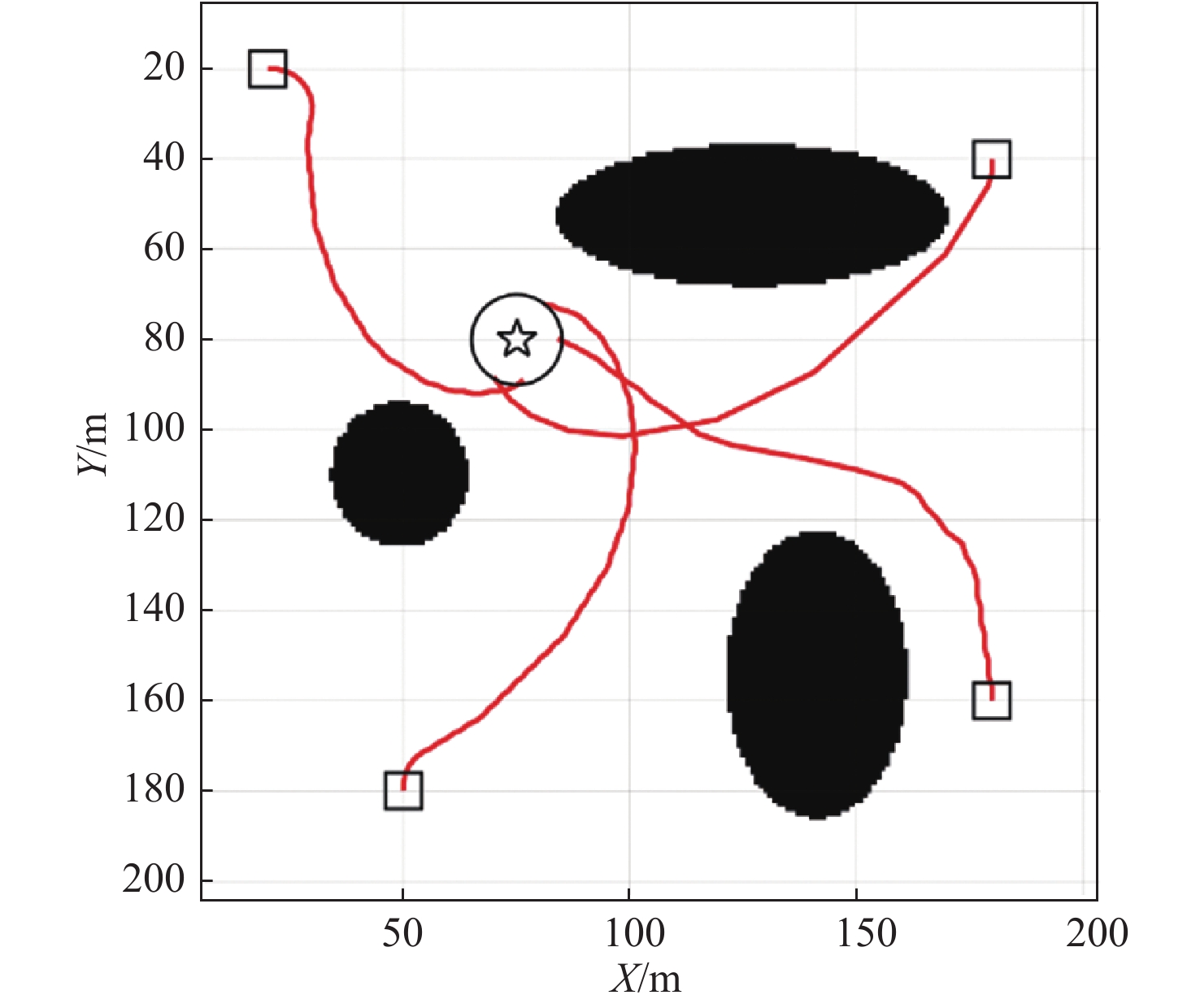
图 8 相同起始点和初始方向，不同目标的计算结果Figure 8. Results of different targets with a same starting point and initial direction可以看出，提出的改进Q学习算法可以达到较好的效果，具有足够的鲁棒性和适应性。图7中，选择4个不同位置和方向的起始点，图8中，从同一个初始点，分别跟踪3个位置和方向不同的目标点，分别开始在线学习，不断更新Q表，自动绕开障碍区域，最终都可以达到目标点。
图9中，红色实线轨迹是USV运动的实际路径，小箭头和数字表示学习阶段的顺序和位置，黑色虚线是每个学习阶段的最优解，而长箭头指出运动目标及其方向。注意到在4的时候，USV的方向有了很大的变化。可能是目标在角落附近后，通过学习过程将USV以更安全的方向导入该角。
另一个值得注意的地方是图中实际位置和学习结果之间的差异。产生差异的原因来自2个方面：一是在运动过程中，传感器获得的状态参数和学习算法在实际操作中的状态参数之间存在时间滞后，当程序循环进入Q表更新步骤时，USV不能停止等待计算结果；二是所模拟的海洋流场的外部环境干扰，以及仿真步长加剧了实际位置和学习结果之间的差异。
5. 结 论
本文采用改进Q学习增强学习算法解决USV目标跟踪问题，通过一系列计算实验验证了该方法的有效性。对具有衰减方程的Q学习算法进行了改进，从而平衡学习过程中的“使用已有行为策略”和“探索新行为策略”。计算结果表明，对于在固定环境和不确定环境中，通过离线和在线学习，该方法提供了一个可靠的不依赖控制对象模型的解决方案。在此基础上，可以进一步地开展相关研究，如处理运动过程中的学习延迟问题，考虑无人艇本身动力学和操作特性对其目标跟踪的影响，开展硬件平台试验等研究。
-
![]()
图 7 不同起始点和初始方向，相同目标的计算结果
Figure 7. Results of different starting points and initial directions with a same target
![]()
图 8 相同起始点和初始方向，不同目标的计算结果
Figure 8. Results of different targets with a same starting point and initial direction
表 1 USV行为参数
Table 1 Chosen USV action velocities
行为 速度(kn) 角速度(rad/s) 左转弯 10 0.26 向前直行 10 0 右转弯 10 −0.26 
下载: 导出CSV
-
[1] 金克帆, 王鸿东, 易宏, 等. 海上无人装备关键技术与智能演进展望[J]. 中国舰船研究, 2018, 13(6): 1–8. JIN K F, WANG H D, YI H, et al. Key technologies and intelligence evolution of maritime UV[J]. Chinese Journal of Ship Research, 2018, 13(6): 1–8 (in Chinese).
[2] LIU Y F, NOGUCHI N. Development of an unmanned surface vehicle for autonomous navigation in a paddy field[J]. Engineering in Agriculture, Environment and Food, 2016, 9(1): 21–26. doi: 10.1016/j.eaef.2015.09.003
[3] 陈铭. 高速无人艇模型及航速/航向解耦控制研究[D]. 哈尔滨: 哈尔滨工程大学, 2011: 1–23. CHEN M. The hydrodynamic models and the decoupling control research in the speed and course of USV[D]. Harbin: Harbin Engineering University, 2011: 1–23 (in Chinese).
[4] 曹诗杰, 曾凡明, 陈于涛. 无人水面艇航向航速协同控制方法[J]. 中国舰船研究, 2015, 10(6): 74–80. doi: 10.3969/j.issn.1673-3185.2015.06.011 CAO S J, ZENG F M, CHEN Y T. The course and speed cooperative control method for unmanned surface vehicles[J]. Chinese Journal of Ship Research, 2015, 10(6): 74–80 (in Chinese). doi: 10.3969/j.issn.1673-3185.2015.06.011
[5] KHAN S G, HERRMANN G, LEWIS F L, et al. Reinforcement learning and optimal adaptive control: an overview and implementation examples[J]. Annual Reviews in Control, 2012, 36(1): 42–59. doi: 10.1016/j.arcontrol.2012.03.004
[6] BRANDON ROHRER. A developmental agent for learning features, environment models, and general robotics tasks[J]. Frontiers in Computational Neuroence, 2011, 5(22): 111–113.
[7] BACA J, HOSSAIN S G M, DASGUPTA P. MODRED: hardware design and reconfiguration planning for a high dexterity modular self-reconfigurable robot for extra-terrestrial exploration[J]. Robotics and Autonomous Systems, 2014, 62(7): 1002–1015. doi: 10.1016/j.robot.2013.08.008
[8] WONG W C, LEE J H. A reinforcement learning-based scheme for direct adaptive optimal control of linear stochastic systems[J]. Optimal Control Applications and Methods, 2010, 31(4): 365–374. doi: 10.1002/oca.915
[9] 徐琰恺, 陈曦,. 基于强化学习的JLQ模型的直接自适应最优控制[J]. 控制与决策, 2008, 23(12): 1359–1362, 1372. doi: 10.3321/j.issn:1001-0920.2008.12.008 XU Y K, CHEN X. Reinforcement learning-based direct adaptive optimal control of JLQ model[J]. Control and Decision, 2008, 23(12): 1359–1362, 1372. doi: 10.3321/j.issn:1001-0920.2008.12.008
[10] WATKINS C J C H, DAYAN P. Technical note: Q-learning[J]. Machine Learning, 1992, 8(3–4): 279–292. doi: 10.1007/BF00992698
[11] DAS P K, BEHERA H S, PANIGRAHI B K. Intelligent-based multi-robot path planning inspired by improved classical Q-learning and improved particle swarm optimization with perturbed velocity[J]. Engineering Science and Technology, an International Journal, 2016, 19(1): 651–669. doi: 10.1016/j.jestch.2015.09.009
[12] WEI Q L, SONG R Z, XU Y C, et al. Iterative Q-learning-based nonlinear optimal tracking control[C]//Proceedings of IEEE Symposium Series on Computational Intelligence. Athens: IEEE, 2016: 1–5.
计量
- 文章访问数: 510
- HTML全文浏览量: 301
- PDF下载量: 59
