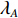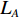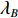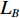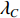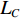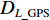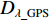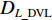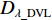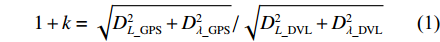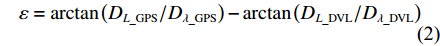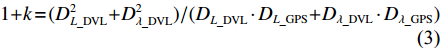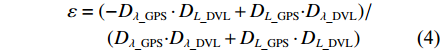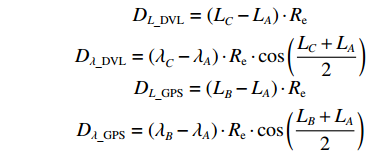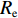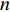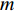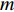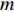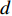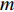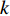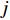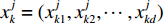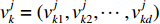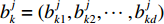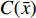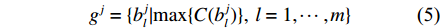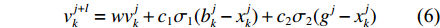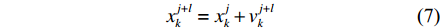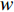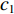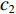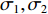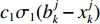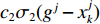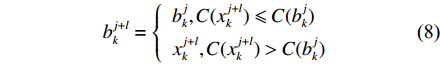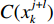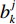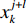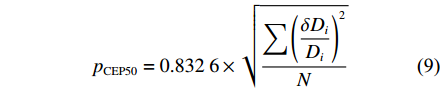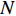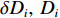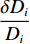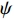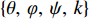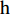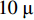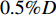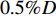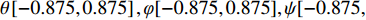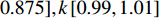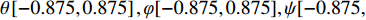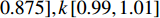Research on offline calibration of DVL parameters based on objective optimization method
-
摘要:目的 为提高水下机器人的水下组合导航定位精度,需要准确标定出捷联惯性导航系统(SINS)和多普勒计程仪(DVL) 之间的安装误差角以及DVL的刻度系数。借鉴多学科优化设计思路,提出基于目标优化方法和传感器实航采集数据的DVL参数离线标定方法。方法 首先,通过跑船实航的方式,开展传统两点法的DVL标定试验和4个航次的FINS/DVL组合导航定位精度验证试验,并将该试验结果作为对比参照;其次,基于离线数据的组合导航过程仿真,使用田口试验法对DVL参数的值域空间进行随机撒点计算,应用响应面模型对计算结果进行截面插值,得到初步的最优解,即DVL标定参数的初值;之后,使用单目标粒子群优化算法,通过迭代优化DVL参数,最终收敛得到最优解,即该方法标定出的DVL参数;最后,使用实航标定出的DVL参数和优化方法得到的DVL参数,分别进行4个航次的FINS/DVL组合导航的离线仿真验证。结果 结果表明:目标优化方法适用于DVL参数的离线标定,与传统两点法标定相比,经过该方法标定后的FINS/DVL组合导航的终点定位误差降低了24.1%,水下组合导航定位精度显著提升。结论 所提方法可为自主式水下机器人(AUV)组合导航系统的DVL标定提供有效手段。Abstract:Objectives In order to improve the positioning accuracy of underwater integrated navigation, it is necessary to accurately calibrate the installation error angle between strapdown inertial navigation system (SINS) and Doppler velocity log (DVL), and the calibration coefficient of DVL. Based on the idea of multidisciplinary optimization design, this paper presents an offline for DVL parameter calibration method based on the target optimization method and sensor real data.Methods First, the traditional two-point method of DVL calibration and four voyages of FINS/DVL integrated navigation positioning accuracy verification are carried out by sailing, which can be used as a reference for comparison with this method. Second, based on a simulation of the integrated navigation process with offline data, the Taguchi test method is used to calculate the value space of the DVL parameters. The response surface model is then used to interpolate the calculation results so as to serve as the initial value of the DVL calibration parameters. Next, a single objective particle flow optimization algorithm is used to optimize the DVL parameters by iteration and converge to the optimal solution as the DVL parameters are calibrated. Finally, using the DVL parameters calibrated by sailing and those obtained through the optimization method, the offline simulation verification of FINS/DVL integrated navigation is carried out in four rounds.Results The results show that the target optimization method is suitable for the offline calibration of DVL parameters. Compared with the traditional two-point method, after calibration by this method, the end-point positioning error of FINS/DVL integrated navigation is reduced by 24.1%, and the positioning accuracy of underwater integrated navigation is significantly improved.Conclusion The proposed method can provide an effective method for the DVL calibration of autonomous underwater vehicle (AUV) integrated navigation systems.
-
0. 引 言
自主式水下机器人(autonomous underwater vehicle,AUV)由于具有体积小、使用成本低、自主作业智能化、保障维护方便、隐蔽性好等诸多优点,在海洋开发和国防领域正发挥着越来越重要的作用[1]。随着AUV应用领域的逐渐扩展,对导航系统的要求越来越高,其必须具备远航程和长航时的高精度导航定位能力。高精度导航定位的性能决定了AUV能否安全作业及返回,是否会影响水下目标定位、海底地形测绘、水下定点布放等作业结果的准确性。
AUV常用的导航方式有: GPS导航、航迹推算、惯性导航、地形匹配、重力场导航和组合导航等。惯性导航系统(INS)因不需要任何外来信息,也不向外辐射任何信息,因而适用于任何工作环境,能实时输出载体的位置、速度和姿态等多种导航参数,并且导航数据平稳、短期稳定性好。目前,光纤捷联惯导(FINS) 属新一代的捷联惯性导航设备(SINS),相对于激光捷联惯导,具有体积小、无噪音、耐冲击、低功耗等优点,在AUV上得到了大量应用。但是INS的误差会随时间积累,为了保证AUV在水下长时间作业的导航定位精度,一般使用由FINS,GPS和多普勒计程仪(DVL)构成的组合导航系统[2-4]。
对于AUV组合导航系统,DVL和SINS在安装(或拆装)后需要对其进行标定,得到其安装误差角和刻度系数,以保证组合导航系统具有较高的水下导航定位精度。于玖成等[5]选取多点参考定位方法,通过利用GPS系统测量AUV准确的经、纬度和速度信息对DVL和SINS的各项误差予以了估计。但对标定试验过程中,因GPS跳动、惯导对准误差、侧向流影响等造成的标定误差却未予考虑。另外,由于两点法标定对试验条件的要求较为苛刻,例如标定试验中AUV载体的水平姿态要求接近于0,开展试验的水域需要具备7 km以上的直线航路等,导致标定试验失败率较高,往往需要多次重复开展DVL标定和组合精度验证试验才能达到FINS/DVL组合导航的精度指标要求,试验耗费时间长、经济成本高。
朱春云等[6]使用卡尔曼在线估计方式,实现了对DVL中3个安装误差角的实时估计。由于安装误差的姿态转换矩阵是实时估计的,这需要AUV持续航行且航向持续变化,才能满足可观性的要求。通过AUV持续转圈或绕“8”字形来进行DVL安装误差角实时在线估计的方法,尚处于实际工程应用前的探索阶段。从目前的实航验证结果来看,采用该方法进行估计其结果的准确性尚不理想,需要进一步开展研究。另外,现阶段的AUV大多以直线或折线航行作业为主,尚不具备持续转圈或绕“8”字形的弹道控制,以及在该机动方式下的避障决策和实时路径规划等功能,无法通过AUV自主航行来完成DVL标定的全程自动化。
本文将借鉴多学科目标优化设计的思想[7],将DVL的安装误差角和刻度系数视为自变量,将一段直线航程的FINS/DVL组合导航的终点定位误差降至最小作为优化目标,通过目标优化算法和手段,找到能够使终点定位误差最小的全局最优解。而这组最优解,即为DVL的标定参数。从而将DVL的参数标定问题转化为在几个自变量的各自值域范围内以及在一定条件的约束下,寻找全域内最优目标的目标优化问题。
1. AUV组合导航系统
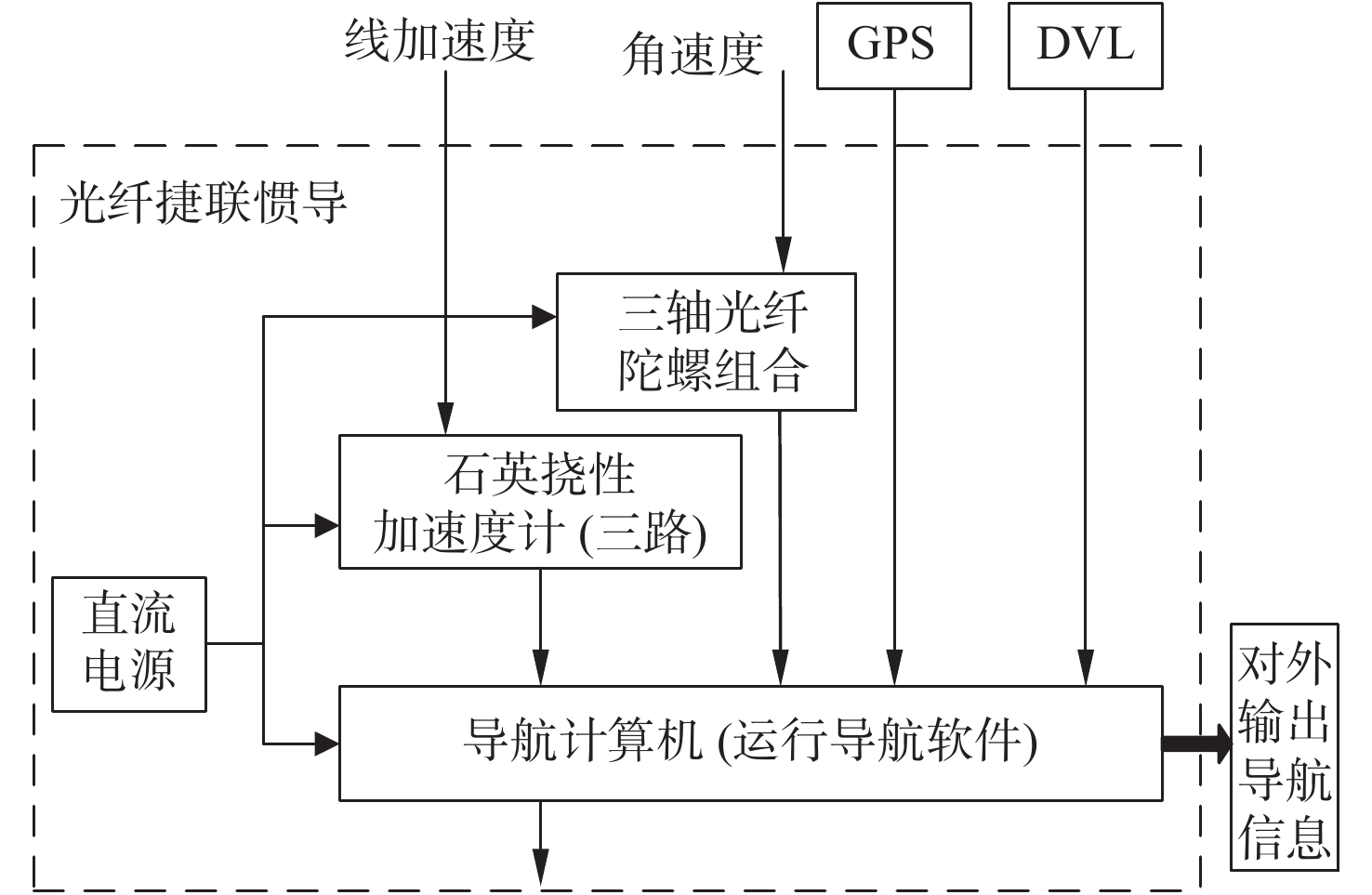
本文所研究的AUV组合导航系统,采用SINS/GPS/DVL组合导航的方式,以为载体提供连续、高精度的导航信息,其系统构成如图1所示。当AUV在水下航行时,使用SINS/ DVL组合导航方式。由于DVL测速误差的存在,水下组合导航的位置误差会随着时间不断积累,从而体现出定位误差随航程的增加而线性增大的特点。故当AUV在水下航行一定路程后,可通过AUV上浮出水或抛出浮标等方式来接收GPS信号,校正AUV当前位置,消除长时间水下导航所积累的位置偏差。校准完成后,AUV继续开展水下作业任务[8]。
2. FINS与DVL间的误差参数标定
针对DVL的参数标定问题,将分别对传统两点法和基于参数优化的DVL标定方法进行介绍。
2.1 传统两点法
假设在标定过程中,AUV的姿态接近于水平,实际航线为线段AB,SINS/DVL组合导航的航迹为线段AC,如图2所示。图中:λ和L分别为经度和纬度,记标定航线起点为A(
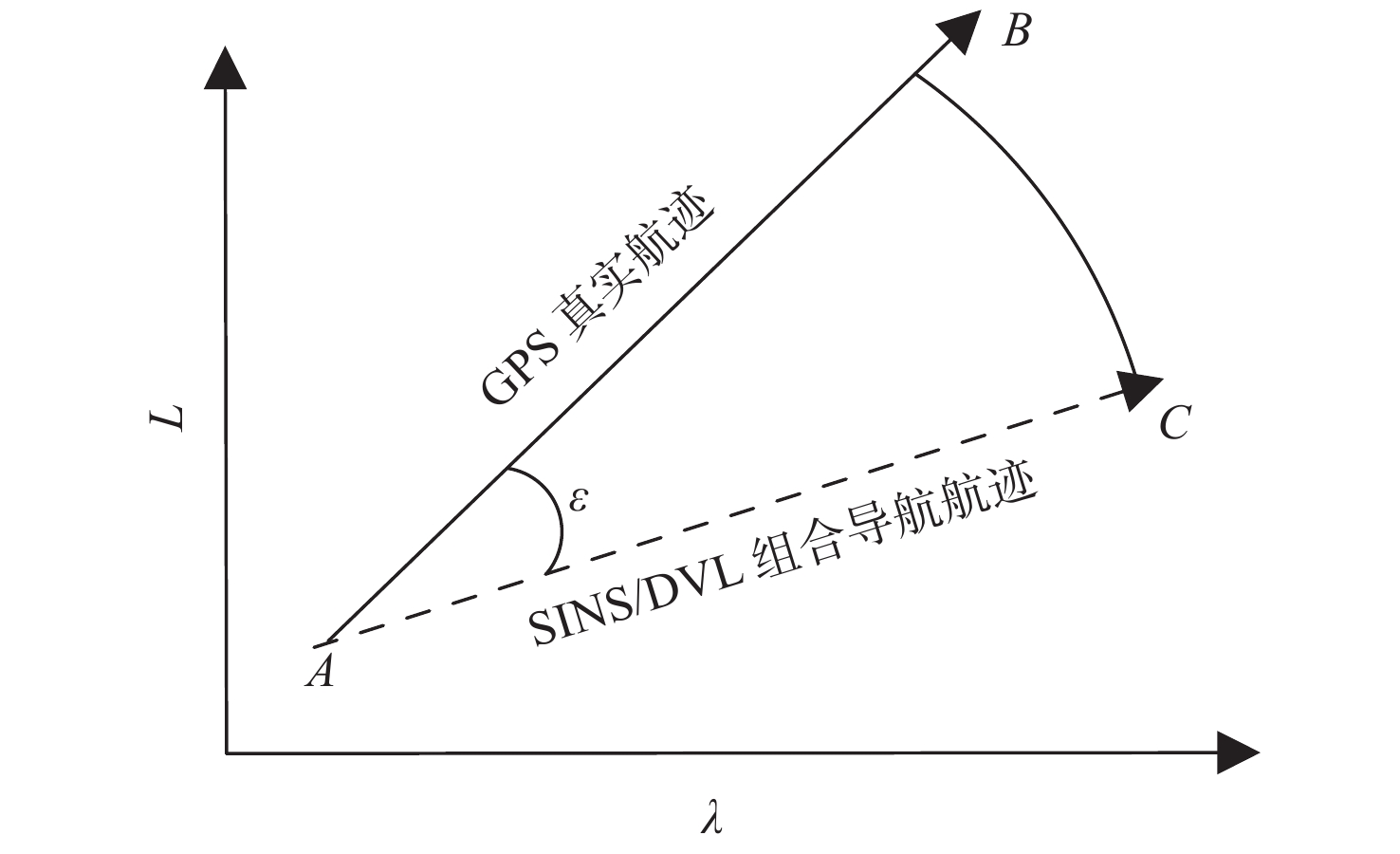
λA ,LA ),终点GPS位置为B(λB ,LB ),终点DVL航位推算位置为C(λC ,LC );GPS航迹的起点与终点间的北向距离为DL_GPS ,东向距离为Dλ_GPS ;SINS/DVL组合导航航迹的起点与终点间的北向距离为DL_DVL ,东向距离为Dλ_DVL 。则INS与DVL间的方位安装误差角 ε 和DVL刻度系数 k 可由以下2种两点法计算得到。
1) 平面几何法。
1+k=√D2L_GPS+D2λ_GPS/√D2L_DVL+D2λ_DVL (1) ε=arctan(DL_GPS/Dλ_GPS)−arctan(DL_DVL/Dλ_DVL) (2) 2) 李万里等[9]提出的地标辅助下的DVL误差标定方法,其假设AUV做匀速直线运动。本文使用该情形下的标定计算公式,简化后得
1+k=(D2L_DVL+D2λ_DVL)/(DL_DVL⋅DL_GPS+Dλ_DVL⋅Dλ_GPS) (3) ε=(−Dλ_GPS⋅DL_DVL+DL_GPS⋅Dλ_DVL)/(Dλ_GPS⋅Dλ_DVL+DL_GPS⋅DL_DVL) (4) 式(1)~式(4)中:
DL_DVL=(LC−LA)⋅ReDλ_DVL=(λC−λA)⋅Re⋅cos(LC+LA2)DL_GPS=(LB−LA)⋅ReDλ_GPS=(λB−λA)⋅Re⋅cos(LB+LA2) 式中,
Re 为地球半径,m。文章所有角度单位均为rad,距离单位均为m。2.2 基于目标优化方法的DVL参数离线标定
2.2.1 拉丁超立方抽样算法
拉丁超立方抽样[10](Latin hypercube sampling)是一种从多元参数分布中近似随机抽样的方法,属于分层抽样技术,常用于计算机实验或蒙特卡罗积分等。在统计抽样中,拉丁方阵是指每行、每列仅包含一个样本的方阵。拉丁超立方则是拉丁方阵在多维中的推广,每个与轴垂直的超平面最多含有一个样本。
假设有
n 个变量(维度),可以将每个变量根据各自的取值范围分为m 个概率相同的子区间,最后在每个子区间内分别进行独立的等概率抽样。此时,可以选取出m 个满足拉丁超立方条件的样本点。具体抽样步骤为:1) 将每一维分成互不重叠的
m 个区间,使每个区间有相同的概率;2) 在每一维里的每一个区间中随机抽取一个点;
3) 再从每一维的步骤2抽取的点集中,随机抽取1个点,将它们组成一个解向量。在步骤2抽取的点集中,不再抽取被步骤3抽取过的点。最终抽取获得m个这样的解向量,即为由拉丁超立方算法抽样得到的样本点。
2.2.2 单目标粒子群优化算法
类似于其他进化算法,单目标粒子群优化算法[11-12]也采用了群体、适应和进化的理念,通过个体间的协作,解决复杂空间中最优解的搜索问题。设
d 维解空间中存在由m 个粒子组成的种群,每个粒子称为单个个体。第k 个粒子在解空间中第j 次迭代时的位置记为xjk=(xjk1,xjk2,⋯,xjkd) 。在空间中以速度vjk=(vjk1,vjk2,⋯,vjkd) 运动搜索,经历的最好位置为bjk=(bjk1,bjk2,⋯,bjkd) ,则对于优化目标函数C(ˉx) ,种群中所有粒子经历的全局最优位置为gj={bjl|max{C(bjl)},l=1,⋯,m} (5) 第k个粒子在进化中其速度和位置的更新公式分别为:
vj+lk=wvjk+c1σ1(bjk−xjk)+c2σ2(gj−xjk) (6) xj+lk=xjk+vj+lk (7) 式中:
w 为惯性权重系数,用于描述粒子的惯性对速度的影响,可以通过调节该参数来平衡粒子群算法的全局搜索能力和局部搜索能力;c1 ,c2 为加速度因子,用于调节算法的收敛速度,一般取值1~2;σ1,σ2 为[0, 1]之间均匀分布的随机数;c1σ1(bjk−xjk) 为粒子在每一次迭代之后对自身的认识部分,描述了粒子的自我认知能力;c2σ2(gj−xjk) 为粒子向整个种群的学习部分,体现了粒子之间的协作。第k个粒子经历的最好位置更新为bj+lk={bjk,C(xj+lk)⩽ (8) 式中,
C({b}_{k}^{j}) ,C({x}_{k}^{j+l}) 分别为解向量为{b}_{k}^{j} 和{x}_{k}^{j+l} 时的目标函数值。2.2.3 实现方法
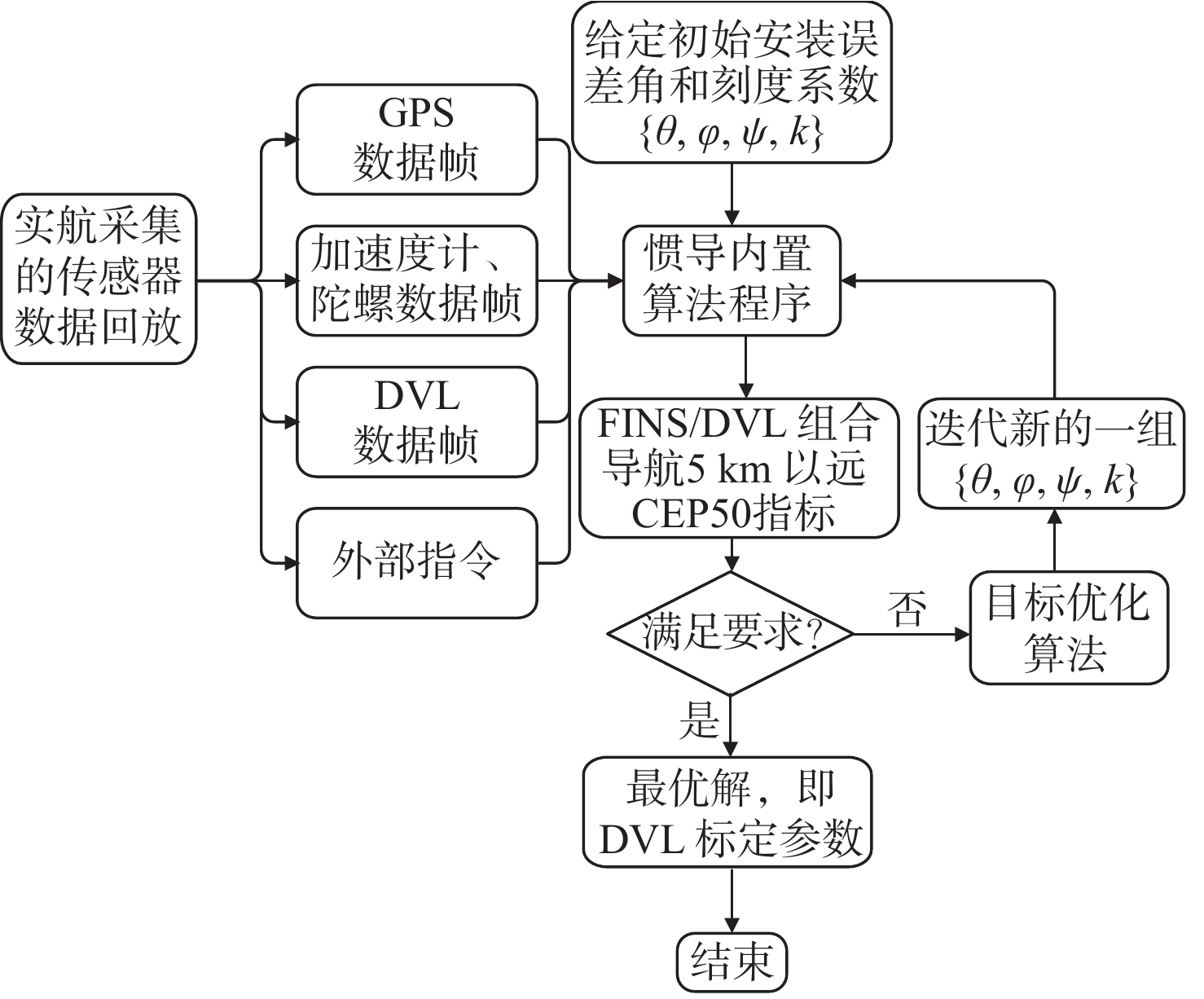
本文提出的DVL离线标定方法,是基于传感器数据回放的组合导航过程离线仿真来实现的。首先,开展4个大于5 km直线航程的跑船试验,对不同工况下的传感器数据进行采集。跑船过程中,在惯导内部的数字信号处理器(DSP)处理板上,对加速度计、陀螺、DVL和GPS,以及外部指令等串口数据帧进行实时解析,5 ms调用内置算法的同时,同步存储这些协议帧。其次,开展离线仿真,对惯导内记数据进行读取回放,加速度计、陀螺、DVL和GPS以及外部指令等数据帧按存储的先后顺序进行数据帧解析,遇到惯性测量单元(IMU)数据帧即视为5 ms算法调用,对惯导内置算法进行调用计算,从而完全复现跑船试验中AUV的对准、水面GPS校准、水下组合导航等导航解算全过程。随后,分析计算FINS/DVL组合导航的定位精度。本文使用5 km以远的定位误差里程比的CEP50指标(简称“CEP50指标”)作为优化目标,即
{p}_{{\rm{C}}{\rm{E}}{\rm{P}}50}=0.832\ 6\times \sqrt{\frac{\displaystyle\sum {\left(\dfrac{{\delta D}_{i}}{{D}_{i}}\right)}^{2}}{N}} (9) 式中:
N 为测量点数;{\delta D}_{i},\;{D}_{i} 分别为第i个测量点的定位误差和航程;\dfrac{{\delta D}_{i}}{{D}_{i}} 为第i个测量点的定位误差里程比。选取DVL的3个安装误差角(记俯仰安装误差角为θ,横滚安装误差角为φ,方位安装误差角为
\psi )和刻度系数k作为设计变量。使用拉丁超立方算法,对整个值域空间进行随机抽样计算,建立响应面模型,分析各设计变量与目标量之间的作用关系及贡献灵敏度等,以进一步优化建立起整个空间关系。之后,使用单目标粒子群优化算法,使用响应面模型插值得到的初值,为各变量分配权重,在限定的\left\{\theta ,\;\varphi ,\;\psi ,\;k\right\} 值域空间范围内进行全域目标优化搜索,最终获得使{p}_{{\rm{C}}{\rm{E}}{\rm{P}}50} 最小的全局最优解,即为该方法标定出的DVL参数。优化流程如图3所示。3. 试验验证
为了验证采用本文所提参数优化方法进行DVL标定的有效性,在某大型水库,通过跑船实航的方式开展了DVL两点法标定及4个航次的FINS/DVL组合导航精度验证,同时进行传感器数据采集。两点法实航标定及精度验证的结果作为本方法的参照对比。使用的器件(或设备)为:0.01 (°)/
{\rm{h}} 的光纤陀螺、10\;{\text{μ}} g的石英加速度计、0.5{\%} D (D为航程)的DVL和3 m定位精度的GPS。惯导与DVL在整个试验过程中安装的位置固定,无拆装。本文将通过以下步骤进行验证。3.1 两点法实航标定
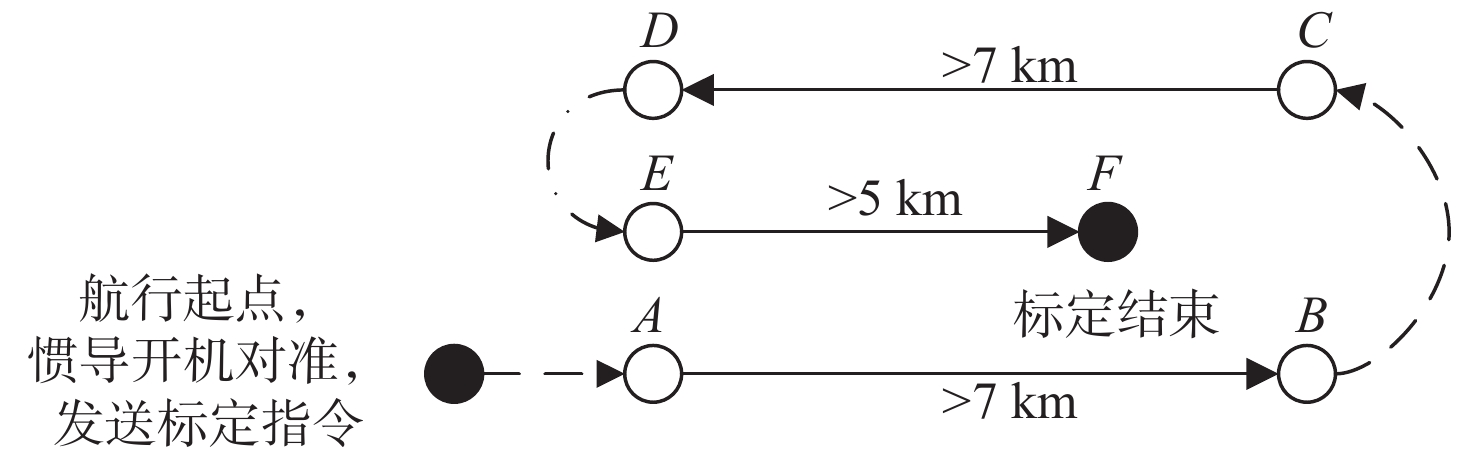
两点法实航标定流程如图4所示。标定时,选择一片开阔的水域,AUV的预设航线为A→B→C→D
→E→F,整个过程由AUV以自主航行模式进行,AUV将沿预设航线以接近匀速直航的方式跑完所有航路点。当AUV航行至标定起点A后,AUV进行第1次GPS校准,校准完成后沿AB在水下定深自主航行。到达B点后AUV上浮至水面进行第2次GPS校准······以此类推,分别在C,D,E和F点进行GPS校准,直至跑完3个直线段后标定结束[13]。标定结果如图5所示。 DVL参数的两点法实航标定结果为[0.0, 0.0,−0.021 2, 1.002 6]。标定验证段,全程6 km,全程最大误差为19.02 m,终点误差为11.89 m,终点误差里程比为0.198%,5 km以远CEP50为0.142%。
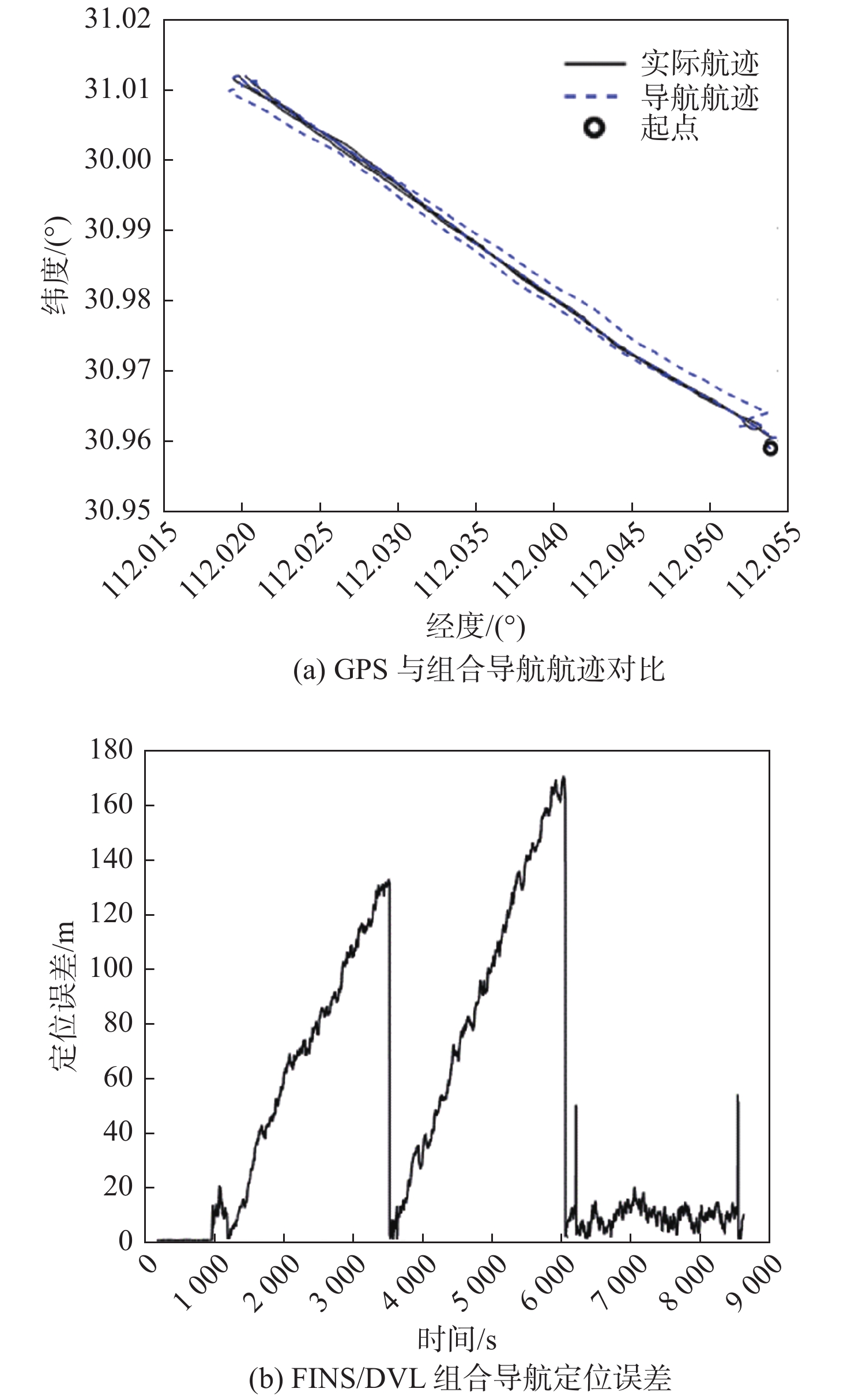
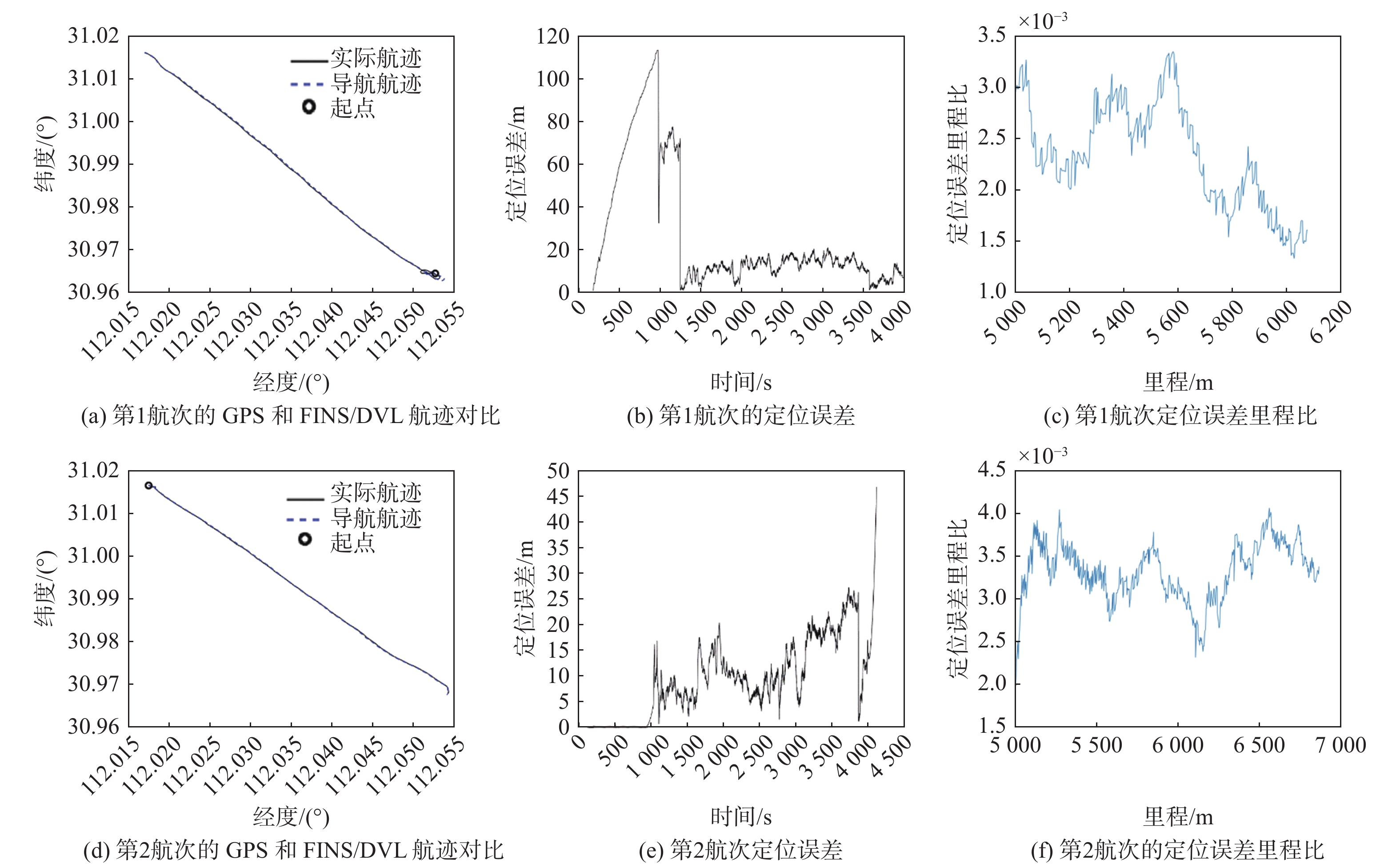
3.2 FINS/DVL组合导航精度的实航验证
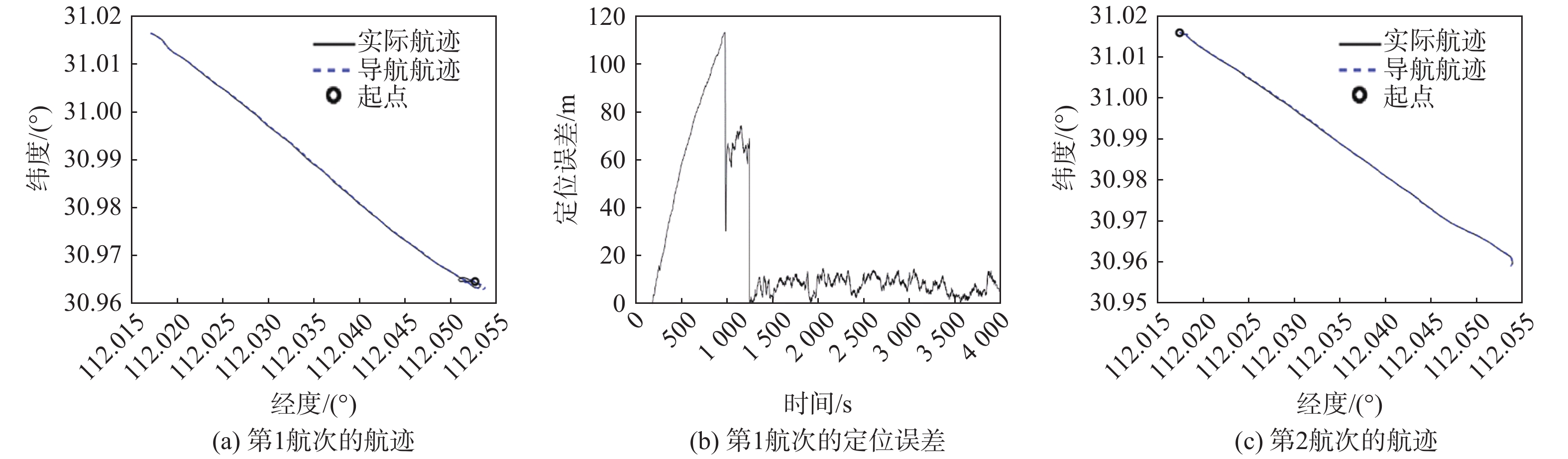
完成DVL安装误差的两点法标定后,使用该标定结果进行了4个航次的FINS/DVL组合导航精度验证实航。试验结果如图6所示。
4个验证航次的实航结果如表1所示。
表 1 4个验证航次的实航结果Table 1. Sailing results of four verification trips航次 对准方式 航程/m 最大误差/m 终点误差/m CEP50(5 km以远) 1 DVL对准 6 053 20.63 10.04 0.002 017 6 2 GPS对准 6 873 26.71 22.6 0.002 779 3 3 GPS对准 5 786 20.93 16.92 0.002 211 1 4 DVL对准 5 796 21.18 21.18 0.002 406 7 之后,使用传统两点法实航标定出的DVL参数和4个验证航次的传感器实航采集数据,开展4个验证航次的FINS/DVL组合导航离线仿真。仿真结果与实航结果一致,这里不再赘述。
3.3 基于目标优化方法的DVL参数离线标定
使用3.2节中实航采集的传感器数据,在Optimus优化软件中搭建优化流程,集成调用数据回放和FINS的内置算法程序,以及调用Matlab进行FINS/DVL组合导航仿真结果的CEP50指标计算。
由于DVL的机械安装精度能够保证在1°以内,其精度优于
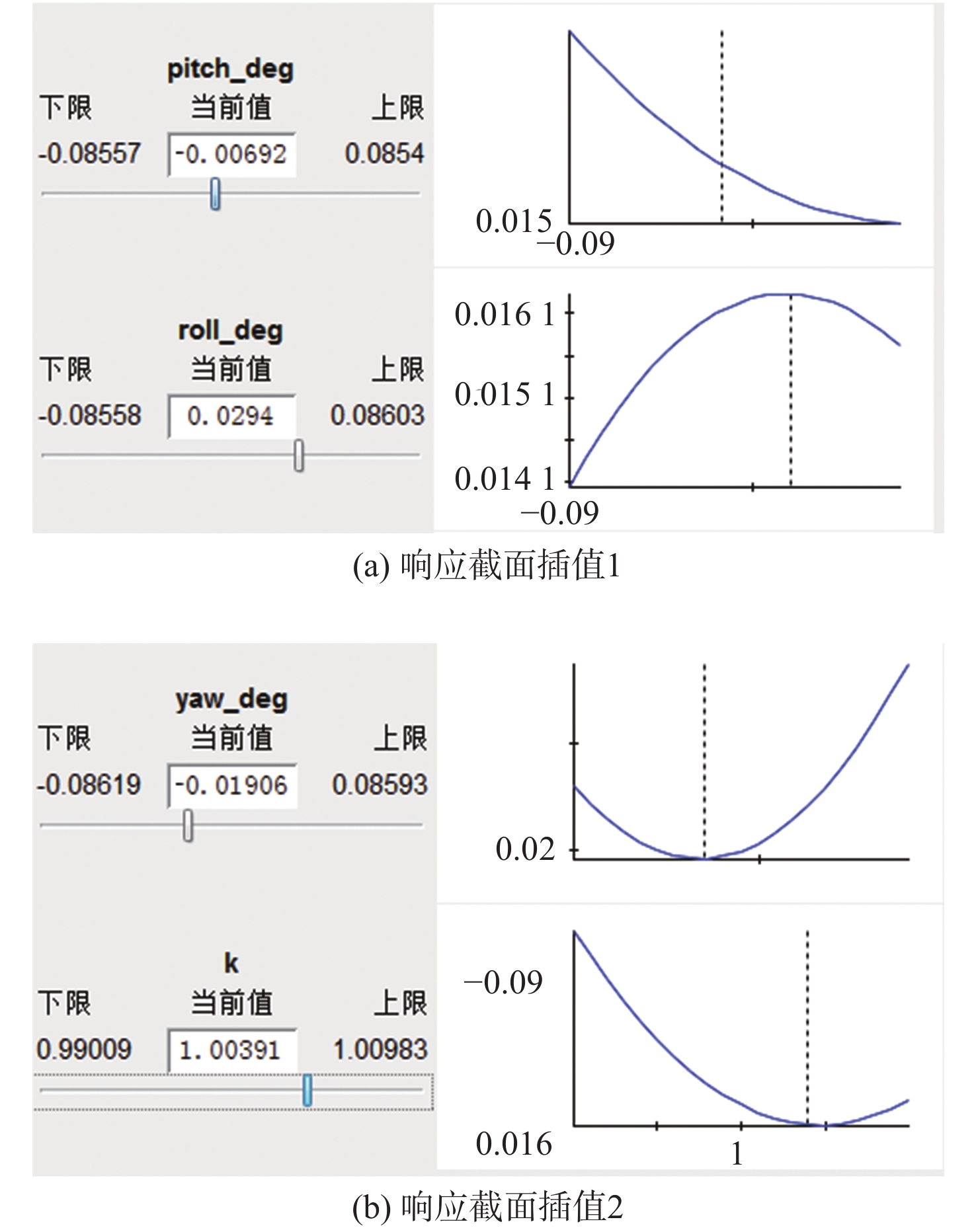
0.5{\%} D ,为保证足够的边界,值域范围设置为\theta \left[-{0.875, 0.875}\right],\varphi [-{0.875, 0.875}],\psi [-0.875, 0.875],k\left[{0.99, 1.01}\right] ,角度均为弧度。以4个验证航次仿真结果的5 km以远的CEP50平均值作为优化目标,选择拉丁超立方算法在整个值域空间内进行100次随机抽样计算,应用响应面模型[14]对计算结果插值出最优解。得到的DVL标定参数为[−0.006 92, 0.029 4, −0.019 06, 1.003 91]。计算过程如图7所示。接下来,以响应面插值得到的最优解[−0.006 92, 0.029 4, −0.019 06, 1.003 91]为初值,使用单目标粒子群优化算法,以4个验证航次仿真结果的5 km以远的CEP50平均值作为优化目标,值域范围仍设置为
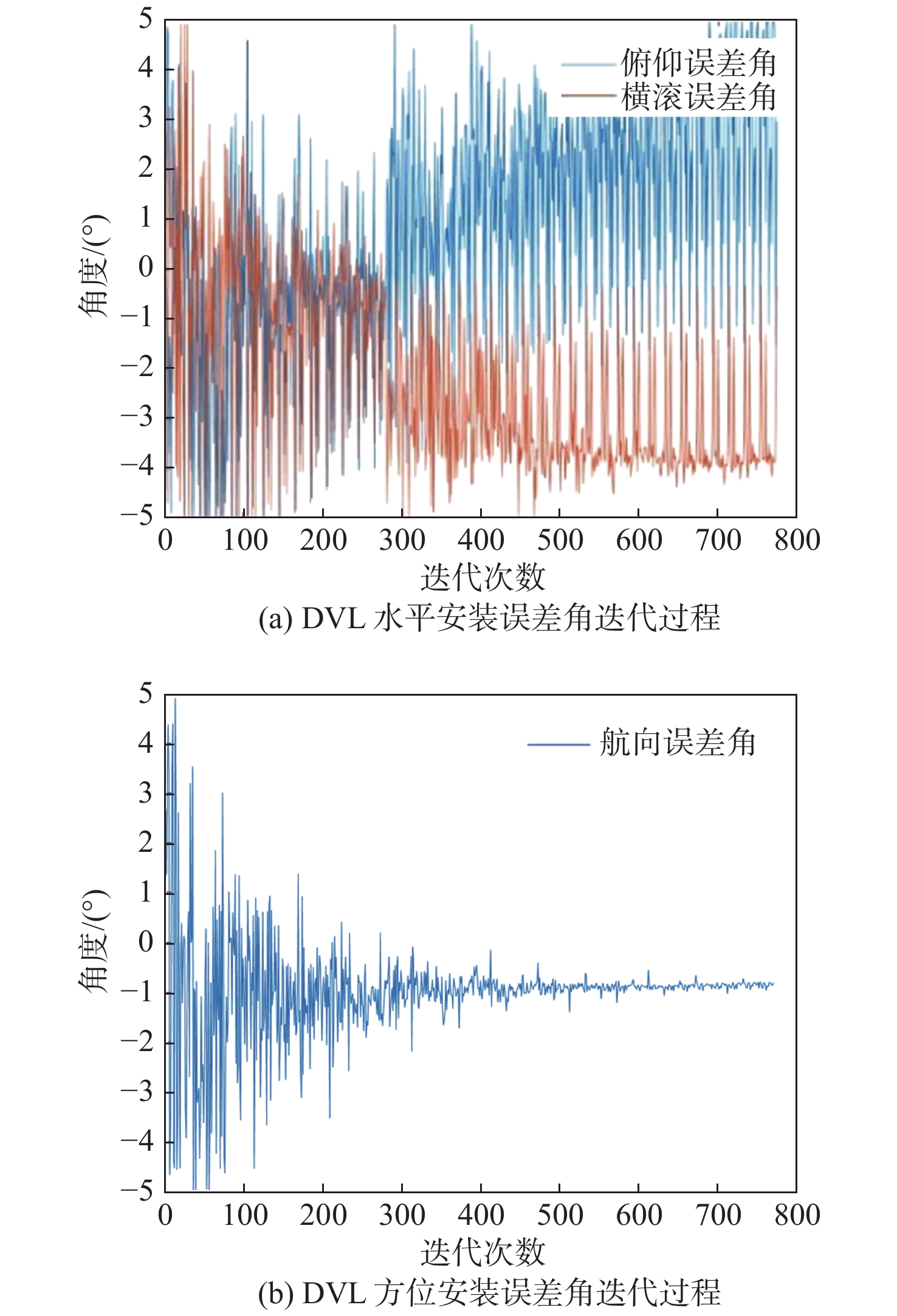
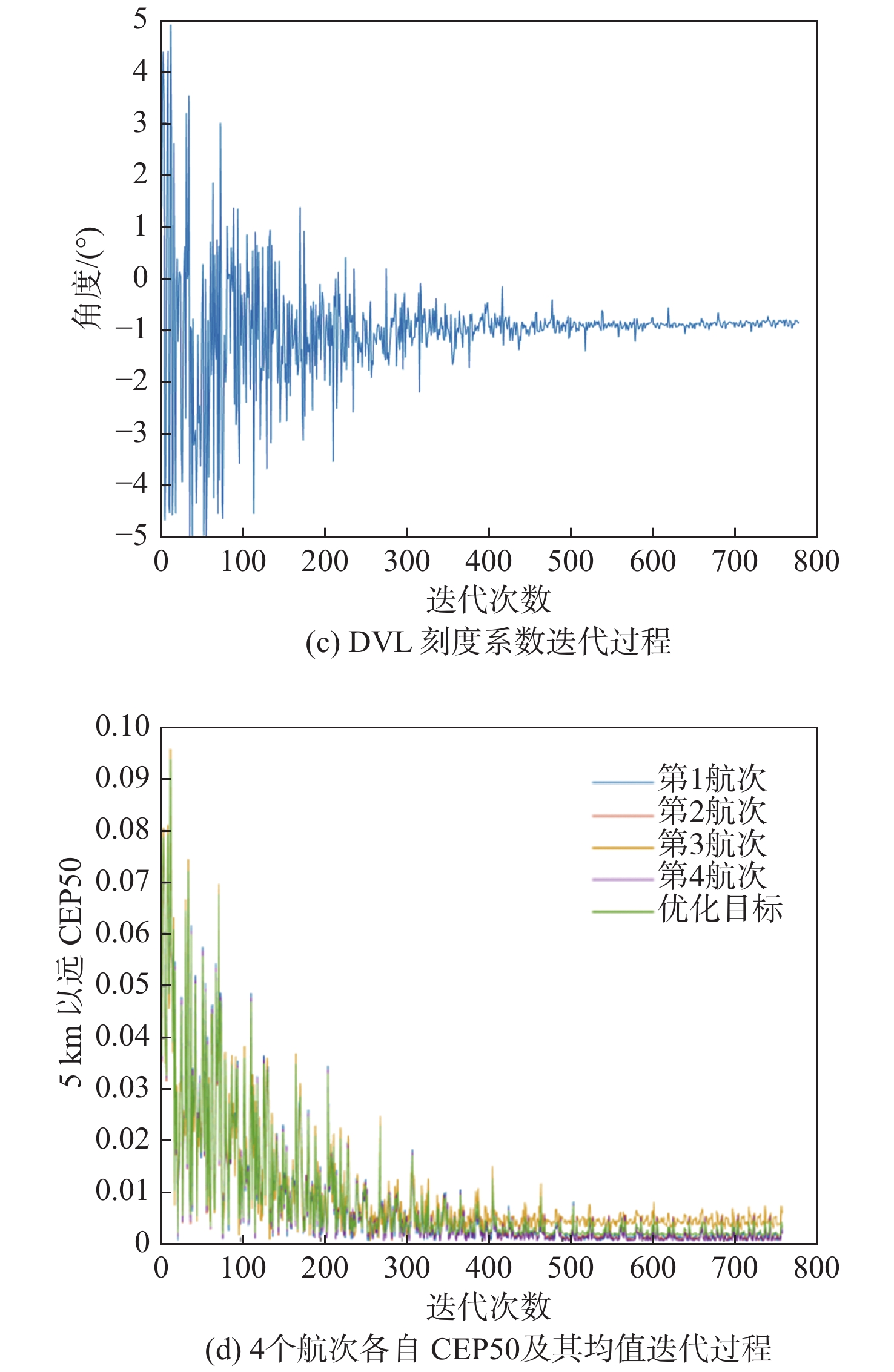
\theta \left[-{0.875,0.875}\right],\varphi [-{0.875,0.875}],\psi [-0.875, 0.875],k\left[{0.99,1.01}\right] ,角度均为弧度,进行单目标优化迭代。计算过程如图8所示。由上述过程,获得的最优解如表2所示。
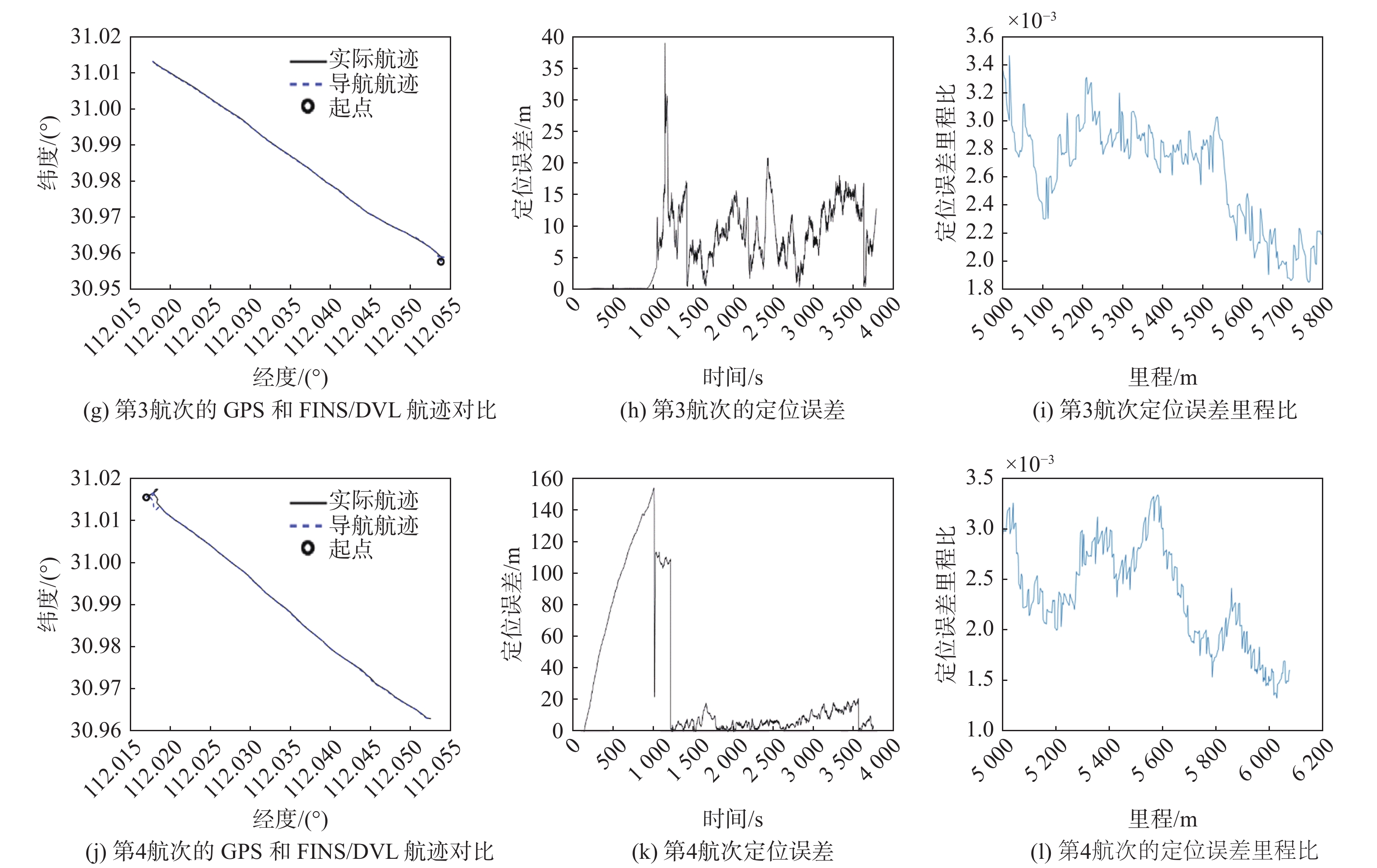
表 2 最优解Table 2. Optimal solution序号 DVL标定参数 FINS/DVL组合导航精度的CEP50指标 俯仰误差角/rad 横滚误差角/rad 航向误差角/rad 刻度系数 第1航次 第2航次 第3航次 第4航次 平均值 762 0.085 35 −0.068 44 −0.014 84 1.005 47 0.001 043 0.001 729 0.002 913 0.001 463 0.001 787 再分别使用4个航次的实航数据,以该最优解作为DVL标定参数,进行FINS/DVL组合导航的离线仿真。4个验证航次的离线仿真结果如图9所示。
3.4 结果对比
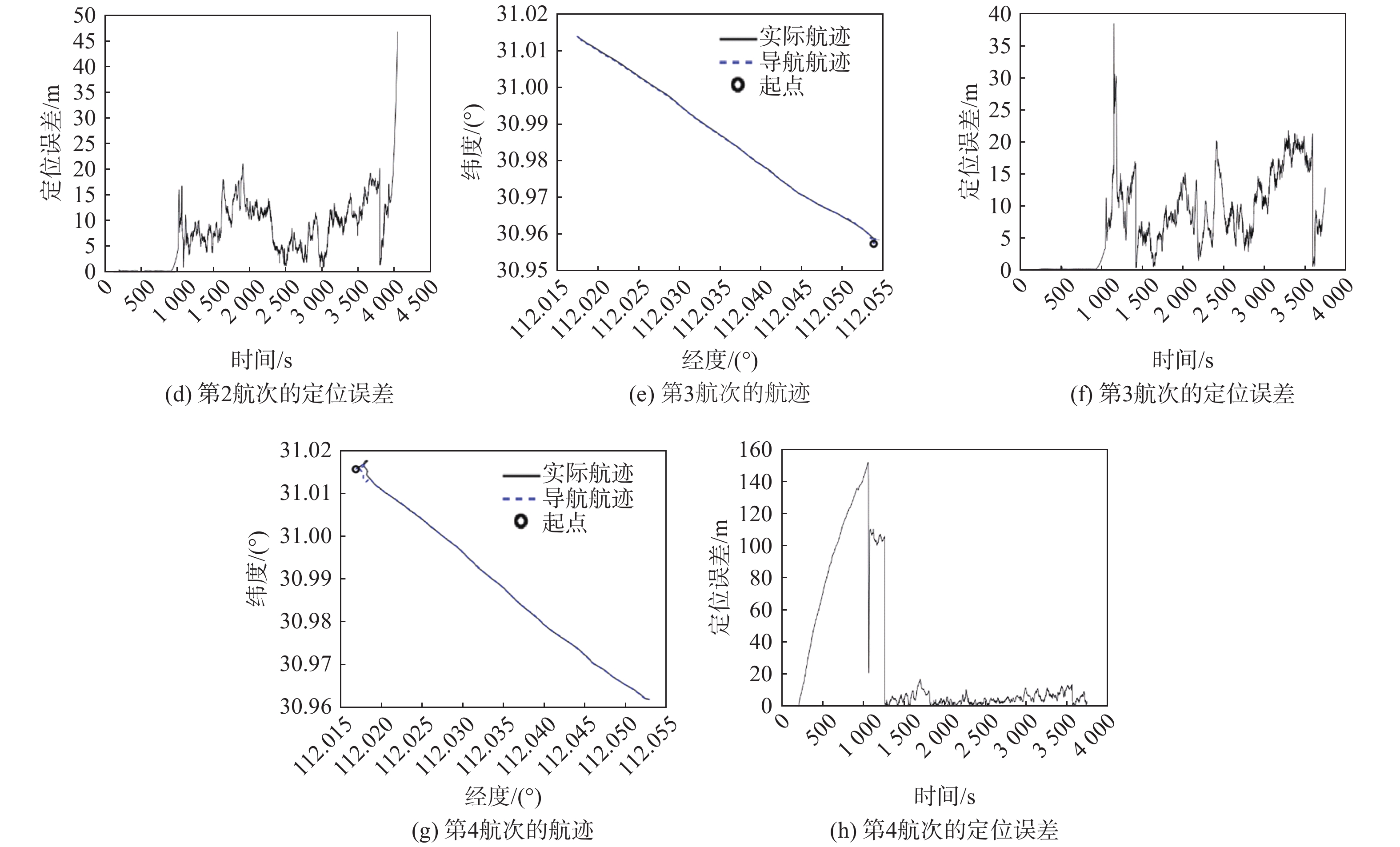
对比分析两点法实航验证的结果、两点法实航标定出的DVL参数进行离线仿真的验证结果,以及目标优化方法获得的DVL参数进行离线仿真的验证结果(表3),可以得到以下结论:1)由于传感器数据回放和惯导内置程序调用的全过程,完全复现了惯导在实际跑船过程中的协议帧接收解析和5 ms定时解算的实时运行状态,故4个航次的两点法实航验证结果与离线仿真结果一致;2)通过使用4个航次的实航数据,分别对两点法实航标定出的DVL参数和以目标优化方法获得的DVL参数等2组DVL参数进行离线仿真,经对比仿真结果可以看出,目标优化方法能够用于DVL参数的离线标定,相比传统的两点法标定,该方法可以大大提高FINS/DVL组合导航的定位精度,5 km以远的定位误差里程比CEP50指标降低了
24.1 %;3)因拉丁超立方算法旨在建立起整个空间关系,但随机抽样数量相对于整个值域空间,样本密度远远不够,因而由响应面插值出的最优解不够准确。故以响应面插值出的最优解作为DVL标定参数得到的仿真结果,其CEP50指标很不理想。表 3 FINS/DVL组合导航的验证结果Table 3. Validation results of FINS / DVL integrated navigation航次 DVL标定参数 4个验证航次的FINS/DVL组合导航定位精度的CEP50指标 俯仰误差角/rad 横滚误差角/rad 航向误差角/rad 刻度系数 第1航次 第2航次 第3航次 第4航次 平均值 跑船实航 0.0 0.0 −0.021 2 1.002 6 0.002 017 0.002 779 0.002 211 0.002 406 0.002 353 跑船仿真 0.0 0.0 −0.021 2 1.002 6 0.002 017 0.002 779 0.002 211 0.002 406 0.002 353 响应面插值解仿真 −0.006 9 0.029 4 −0.019 1.003 91 0.001 67 0.002 629 0.005 43 0.002 291 0.003 005 最优解仿真 0.085 35 −0.068 4 −0.014 8 1.005 5 0.001 043 0.001 729 0.002 913 0.001 463 0.001 787 4. 结 语
本文针对AUV组合导航系统的DVL安装误差,提出了基于目标优化方法和传感器实航数据的DVL参数离线标定方法。首先,通过跑船实航的方式,进行了传统两点法的DVL标定和4个航次的FINS/DVL组合导航定位精度验证,作为本方法的对比参照。其次,基于实航数据的离线仿真,使用拉丁超立方算法对DVL参数的值域空间进行随机抽样计算,应用响应面模型对计算结果进行截面插值,得到了初步的最优解,即DVL标定参数的初值。之后,使用单目标粒子群优化算法,通过迭代优化DVL参数,最终收敛至最优解,即该方法标定出的DVL参数。最后,使用实航标定出的DVL参数和优化方法得到的DVL参数,分别进行了4个航次的FINS/DVL组合导航的离线仿真验证。仿真验证结果表明,目标优化方法适用于DVL参数的离线标定,相比传统的两点法标定,经过该方法标定后,FINS/DVL组合导航的5 km以远定位误差里程比CEP50指标降低了24.1%,水下组合导航定位精度显著提升。通过对比不同的DVL标定方法对水下组合导航定位精度的影响,为AUV组合导航系统的DVL标定提供了有效手段。
-
表 1 4个验证航次的实航结果
Table 1 Sailing results of four verification trips
航次 对准方式 航程/m 最大误差/m 终点误差/m CEP50(5 km以远) 1 DVL对准 6 053 20.63 10.04 0.002 017 6 2 GPS对准 6 873 26.71 22.6 0.002 779 3 3 GPS对准 5 786 20.93 16.92 0.002 211 1 4 DVL对准 5 796 21.18 21.18 0.002 406 7 表 2 最优解
Table 2 Optimal solution
序号 DVL标定参数 FINS/DVL组合导航精度的CEP50指标 俯仰误差角/rad 横滚误差角/rad 航向误差角/rad 刻度系数 第1航次 第2航次 第3航次 第4航次 平均值 762 0.085 35 −0.068 44 −0.014 84 1.005 47 0.001 043 0.001 729 0.002 913 0.001 463 0.001 787 表 3 FINS/DVL组合导航的验证结果
Table 3 Validation results of FINS / DVL integrated navigation
航次 DVL标定参数 4个验证航次的FINS/DVL组合导航定位精度的CEP50指标 俯仰误差角/rad 横滚误差角/rad 航向误差角/rad 刻度系数 第1航次 第2航次 第3航次 第4航次 平均值 跑船实航 0.0 0.0 −0.021 2 1.002 6 0.002 017 0.002 779 0.002 211 0.002 406 0.002 353 跑船仿真 0.0 0.0 −0.021 2 1.002 6 0.002 017 0.002 779 0.002 211 0.002 406 0.002 353 响应面插值解仿真 −0.006 9 0.029 4 −0.019 1.003 91 0.001 67 0.002 629 0.005 43 0.002 291 0.003 005 最优解仿真 0.085 35 −0.068 4 −0.014 8 1.005 5 0.001 043 0.001 729 0.002 913 0.001 463 0.001 787 -
[1] 周凯, 易杏甫. 水下机器人概述和发展应用前景[J]. 科技致富向导, 2010(16): 587–588. ZHOU K, YI X P. Overview and application prospect of underwater vehicle[J]. Electronic Technology, 2010(16): 587–588 (in Chinese).
[2] 黄鸣敏. 组合导航系统在水下潜器中的应用[D]. 南京: 南京理工大学, 2007: 1-2. HUANG M M. Application of integrated navigation system in underwater vehicle[D]. Nanjing: Nanjing University of Technology, 2007: 1-2 (in Chinese).
[3] HARTMAN R, HAWKINSON W, SWEENEY K. Tactical underwater navigation system (TUNS)[C]//2008 IEEE/ION Position, Location and Navigation Symposium. Monterey, CA, USA: IEEE, 2008: 898-911.
[4] BROATCH S A, HENLEY A J. An integrated navigation system manager using federated Kalman filtering[C]//Proceedings of the IEEE 1991 National Aerospace and Electronics Conference NAECON 1991. Dayton, OH, USA: IEEE, 1991: 422-426.
[5] 于玖成, 何昆鹏, 王晓雪. SINS/DVL组合导航系统的标定[J]. 智能系统学报, 2015, 10(1): 143–148. YU J C, HE K P, WANG X X. Calibration for strapdown inertia navigation/Doppler velocity log integrated navigation system[J]. CAAI Transactions on Intelligent Systems, 2015, 10(1): 143–148 (in Chinese).
[6] 朱春云, 庄广琛, 宋雅兰, 等. DVL安装角估计方法在水下组合导航系统中的应用[J]. 中国惯性技术学报, 2011, 19(1): 75–78. ZHU C Y, ZHUANG G C, SONG Y L, et al. DVL installation angle estimation and application in underwater integrated navigation system[J]. Journal of Chinese Inertial Technology, 2011, 19(1): 75–78 (in Chinese).
[7] 张贵军, 丁情, 王柳静, 等. 柔性车间生产排产调度优化方法[J]. 计算机科学, 2018, 45(2): 269–275. doi: 10.11896/j.issn.1002-137X.2018.02.046 ZHANG G J, DING Q, WANG L J, et al. Optimization method of production scheduling in flexible job[J]. Computer Science, 2018, 45(2): 269–275 (in Chinese). doi: 10.11896/j.issn.1002-137X.2018.02.046
[8] 俞建成, 张艾群, 王晓辉, 等. 基于多普勒和光纤陀螺水下机器人导航系统研究[J]. 船海工程, 2006, 35(2): 105–108. doi: 10.3963/j.issn.1671-7953.2006.02.031 YU J C, ZHANG A Q, WANG X H, et al. Research on underwater vehicles navigation system based on DVL and fiber-optic gyro[J]. Ship & Ocean Engineering, 2006, 35(2): 105–108 (in Chinese). doi: 10.3963/j.issn.1671-7953.2006.02.031
[9] 李万里, 陈明剑, 李俊毅, 等. 惯性/多普勒组合导航回溯算法研究[M]. 武汉: 中国地质大学出版社, 2016: 20-24. LI W L, CHEN M J, LI J Y, et al. Research on the Backtracking algorithm of inertial/Doppler integrated navigation[M]. Wuhan: China University of Geosciences Press, 2016: 20-24 (in Chinese).
[10] 季宁, 张卫星, 于洋洋, 等. 基于最优拉丁超立方抽样方法和NSGA–II算法的注射成型多目标优化[J]. 工程塑料应用, 2020, 48(3): 72–77. doi: 10.3969/j.issn.1001-3539.2020.03.013 JI N, ZHANG W X, YU Y Y, et al. Multi-objective optimization of injection molding based on optimal Latin hypercube sampling method and NSGA–II algorithm[J]. Engineering Plastics Application, 2020, 48(3): 72–77 (in Chinese). doi: 10.3969/j.issn.1001-3539.2020.03.013
[11] KENNEDY J, EBERHART R C. Particle swarm optimization[C]//Proceedings of the IEEE International Conference on Neural Networks. Perth, Australia, NJ: IEEE, 1995: 1942-1948.
[12] 王婷, 隋江华. 改进粒子群算法的传感器网络覆盖分布优化[J]. 辽宁工程技术大学学报(自然科学版), 2020, 39(3): 280–286. WANG T, SUI J H. Optimization of sensor network coverage distribution improved particle swarm optimization[J]. Journal of Liaoning Technical University (Natural Science), 2020, 39(3): 280–286 (in Chinese).
[13] 吕志刚. 基于SINS/DVL/GPS的AUV组合导航标定方法的研究及其误差分析[J]. 舰船电子工程, 2018, 38(6): 33–36. doi: 10.3969/j.issn.1672-9730.2018.06.009 LYU Z G. Research on SINS/DVL/GPS integrated navigation system calibration method and the error analysis of AUV[J]. Ship Electronic Engineering, 2018, 38(6): 33–36 (in Chinese). doi: 10.3969/j.issn.1672-9730.2018.06.009
[14] 余世浩, 何星明, 张国英. 基于响应面模型和NSGA–Ⅱ算法的注塑成型工艺优化[J]. 塑性工程学报, 2014, 21(3): 15–19, 141. doi: 10.3969/j.issn.1007-2012.2014.03.004 YU S H, HE X M, ZHANG G Y. Processing optimization of injection molding based on response surface model and NSGA–II algorithm[J]. Journal of Plasticity Engineering, 2014, 21(3): 15–19, 141 (in Chinese). doi: 10.3969/j.issn.1007-2012.2014.03.004



 下载:
下载: