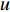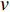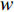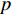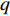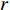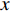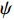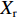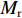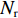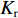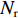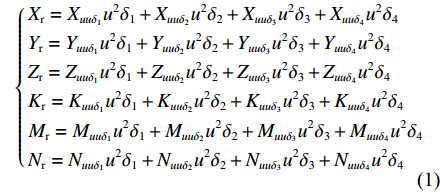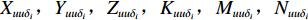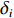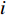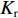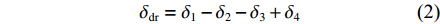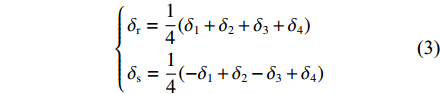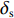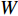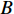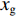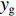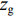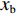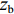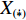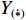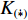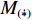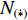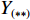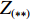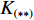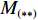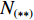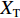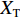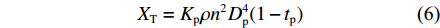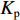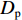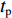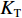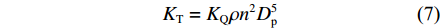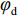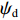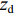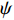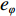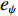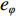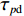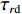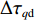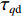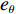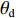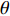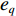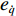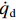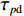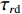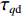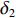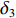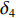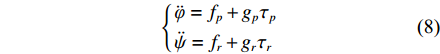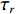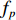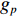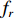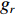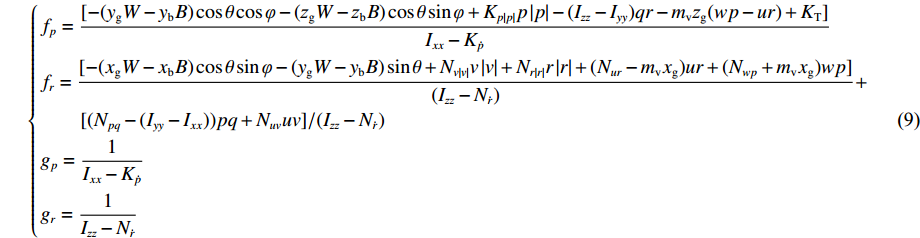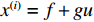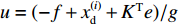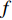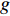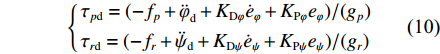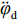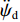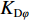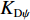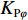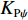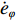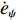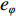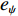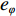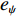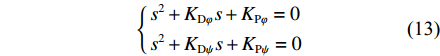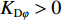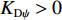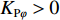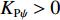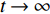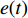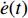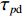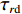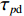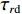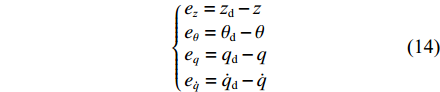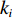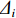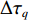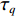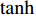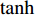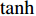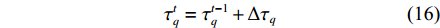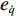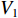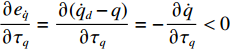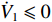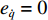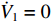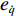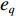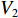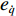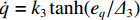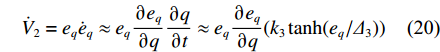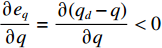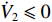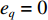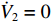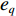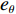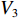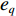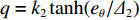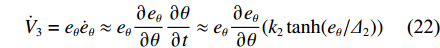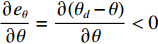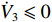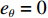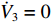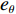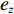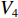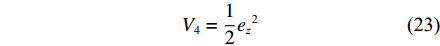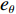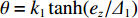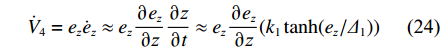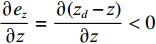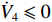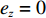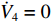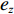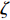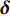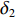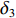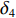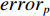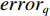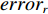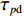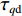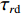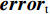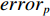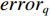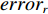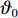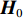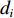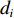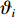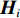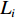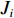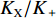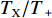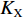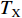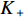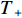0.   引　言

在过去的几十年间，随着海洋工程装备的不断发展，各种各样的水下航行器被广泛应用于海洋工程与科研领域。自主式水下航行器（autonomous underwater vehicle，AUV）作为应用最为广泛的水下装备之一，在海洋调查、水下监测等方面发挥着巨大作用^[1-2]。

为了进一步提升自主式水下航行器的性能，国内外学者提出了诸多方法，其中改进水下航行器的尾部操纵面以提高其操纵性及水动力性能就是其中之一，X形舵（以下简称“X舵”）便是这种想法下的产物。X舵的舵叶布局呈“X”形^[3]，其4个舵叶可独立运行，相比传统的十字形舵（以下简称“十字舵”）具有舵效高、机动性强、噪声低、抗沉性强等优点。但由于X舵任意操纵面的运动都会对水下航行器的偏航与纵倾运动产生影响，有着较为复杂的操纵特性，故最初并未得到广泛应用。近年来，随着自动化软、硬件水平的提升与X舵技术的成熟，X舵的构型已逐渐从理论研究阶段走向实际应用，当前正在服役的德国212A型以及瑞典的“哥特兰”级潜艇均采用的是X形尾舵。除军事用途外，X舵水下航行器也被广泛应用于科研与民用领域^[4]。

当前，关于X舵的研究可以分为2个部分。第1个部分是实现X舵的基本控制。Zhang等^[5]基于能量最低准则，提出了X舵在双舵、三舵以及四舵时的舵分配方案，并利用仿真试验验证了该舵分配方案的有效性；Xia等^[6]基于滑模控制提出了X舵水下航行器在传感器失效情况下的最优鲁棒轨迹跟踪，并通过仿真试验验证了其有效性。第2个部分的研究是深度挖掘算法以充分发挥X舵的优势。Wang等^[7]基于双环增量反馈控制并结合非线性规划，实现了X舵水下航行器的容错控制。

当前国内外发表的有关X舵的研究大多集中在X舵的定性介绍、建模以及X舵的舵分配方案上，鲜有涉及如何利用X舵去抑制水下航行器的横滚，以及X舵相比十字舵在性能上的优势的定量分析。因此，本文将根据XAUV在航行过程中存在的横滚角过大的问题，提出一种考虑横滚动力学的反馈线性化PD横滚与航向动力学控制器，并结合增量反馈控制的深度动力学控制器，在实现XAUV航向与深度控制的同时，基于X舵的差动舵角抑制XAUV的横滚，并利用水池试验验证本文所提控制方法的有效性。最后，根据XAUV艉舵构型可转换的特点，在操纵性水池中开展系列操纵性试验并根据试验结果对相同艇体模型下X舵相比十字舵的性能优势进行定量分析。

1.   XAUV设计与建模

1.1   XAUV设计

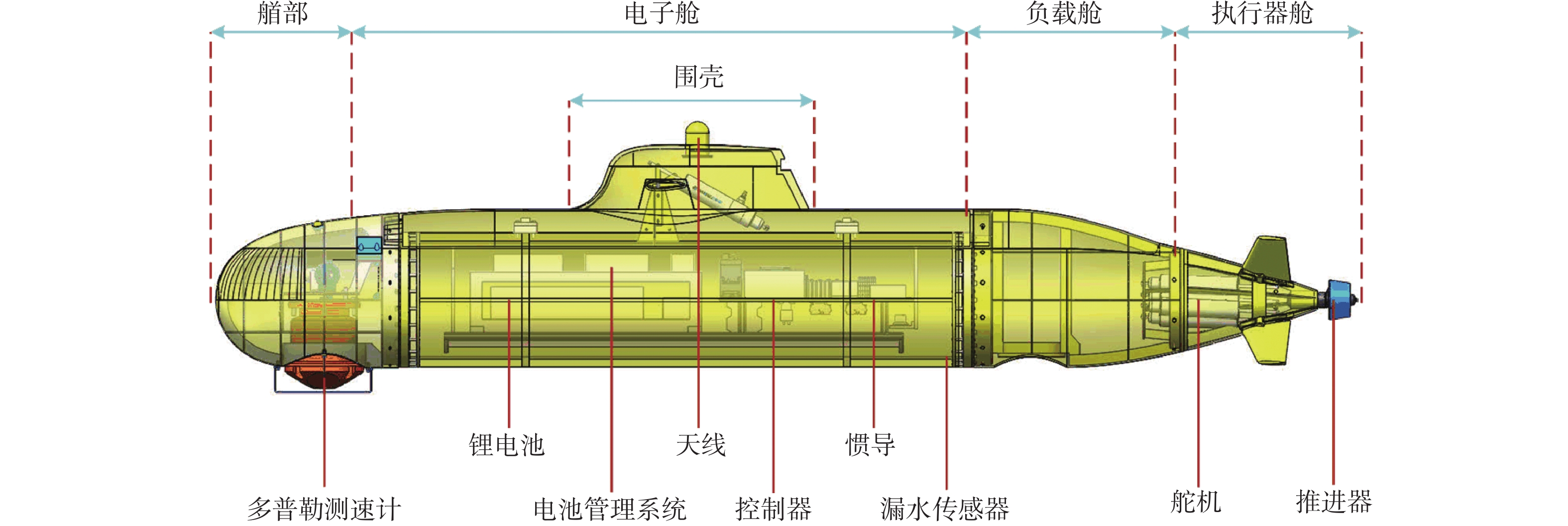
本文研究的XAUV总长2.964 m，总重231.9 kg，采用模块化设计理念，分为艏部、电子舱、负载舱、执行器舱和围壳5个部分，具体的参数如表1所示，系统结构如图1所示。XAUV具备自主航行与远程遥控2种操作模式：在水面航行状态，操作人员可以通过集成于地面控制站的WIFI远程控制XAUV；当需要进行水下航行时，操作人员首先通过地面控制站将任务下达给XAUV，然后再将XAUV切换到自主模式去执行水下任务；待水下任务执行完毕后，XAUV浮出水面并等待下一个任务指令。

表  1  X舵自主式水下航行器主要参数

Table  1.  Main parameters of XAUV

参数	数值
艇长L/m	2.964
艇宽Bw /m	0.380
艇高H/m	0.443
重心纵向位置	船体中心沿船艏0.147 m处
水下全排水体积$\nabla$/m3	0.229 5
总质量mv /kg	231.9
最大推力XTmax /N	75.6
X轴转动惯量Ixx /(kg·m2)	10.260
Y轴转动惯量Iyy /(kg·m2)	166.684
Z轴转动惯量Izz /(kg·m2)	165.220

下载: 导出CSV 

| 显示表格

图  1  X舵自主式水下航行器的布局示意图

Figure  1.  Layout of XAUV

下载: 全尺寸图片 幻灯片

在传感器配置方面，XAUV配备有惯性导航系统（INS）、多普勒测速仪（DVL）与全球定位系统（GPS），通过数据融合算法为其提供位置、姿态和速度等方面的辅助数据，从而为AUV的精确控制提供数据支撑。在能源配置方面，XAUV配备有锂电池。作为唯一的能量来源，能源系统中配备有电池管理系统（BMS）用于实时监控锂电池的健康状况、电流、电压、温度等信息，以保证能源系统的安全。

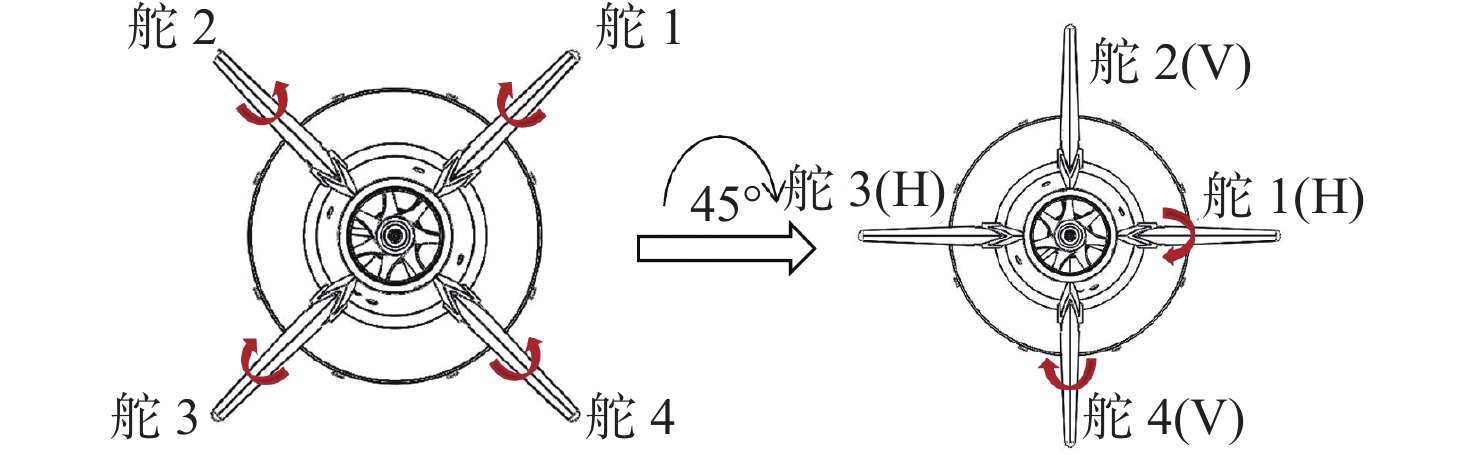
在XAUV的执行器舱中，搭载有4个独立的舵机，可以根据控制器的指令要求独立完成操舵任务。根据不同的任务需求，尾部执行器舱还可顺时针旋转45°，从而将尾部构型转换为十字舵，如图2所示。因此，XAUV还可以为X舵与十字舵之间的性能对比研究提供试验平台。

图  2  X舵与十字舵构型示意图

Figure  2.  Layout of X-rudder and cruciform rudder

下载: 全尺寸图片 幻灯片

1.2   XAUV坐标系建立

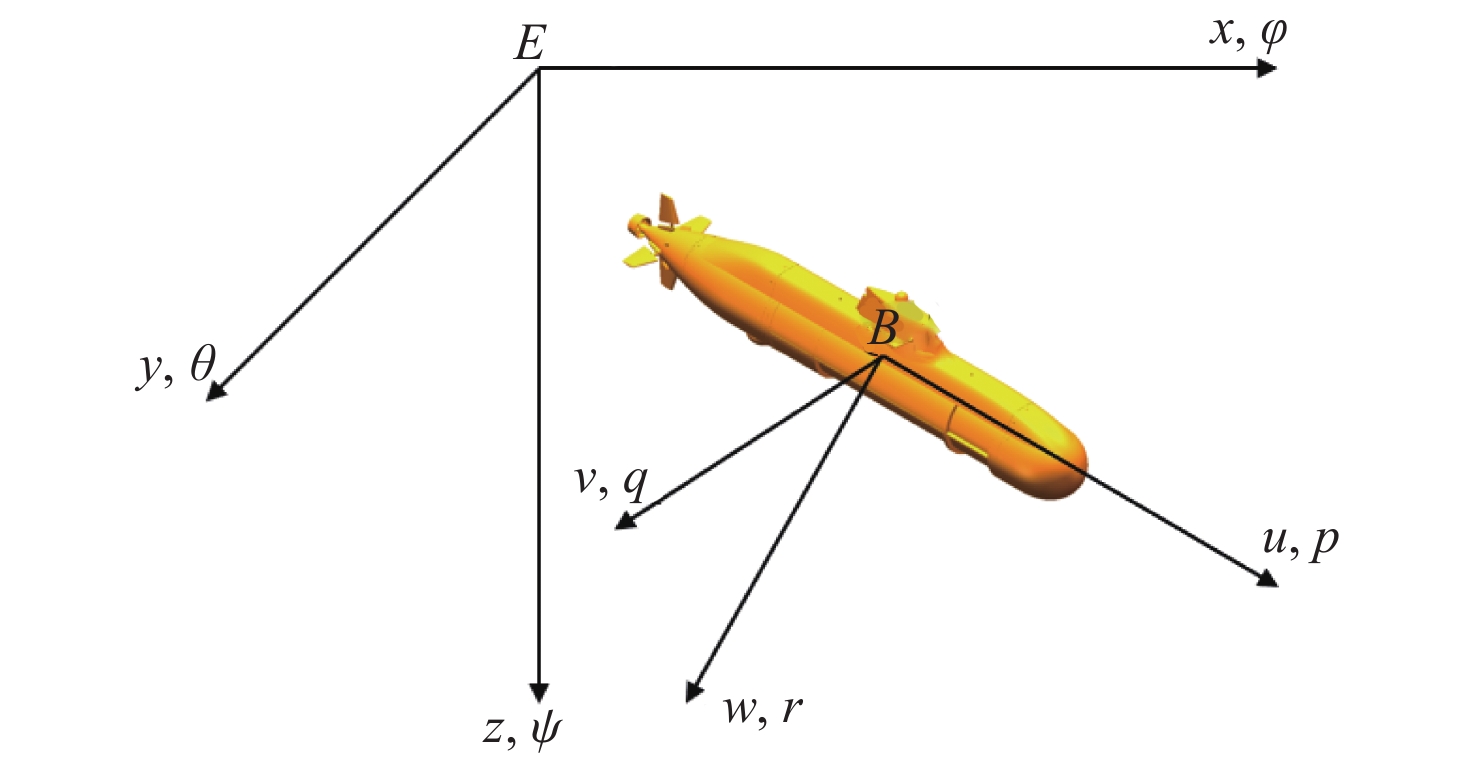
为了描述XAUV在水下的六自由度运动，同时参考ITTC和SNAME所推荐的坐标系与名词术语，本文为XAUV建立了固定坐标系E和运动坐标系B，如图3所示。图中：$u$，$v$，$w$分别为XAUV的纵向速度、横向速度与垂向速度；$p$，$q$，$r$分别为XAUV的横滚角速度、纵倾角速度与偏航角速度；$x$，$y$，${\textit{z}}$分别代表XAUV在固定坐标系 E中的纵向位置、横向位置与垂向位置；$\varphi$，$\theta$，$\psi$ 则为XAUV在固定坐标系 E中的横滚角、纵倾角与艏向角。

图  3  XAUV的坐标系定义

Figure  3.  Definition of XAUV's coordinate system

下载: 全尺寸图片 幻灯片

1.3   X舵舵力分析与模型建立

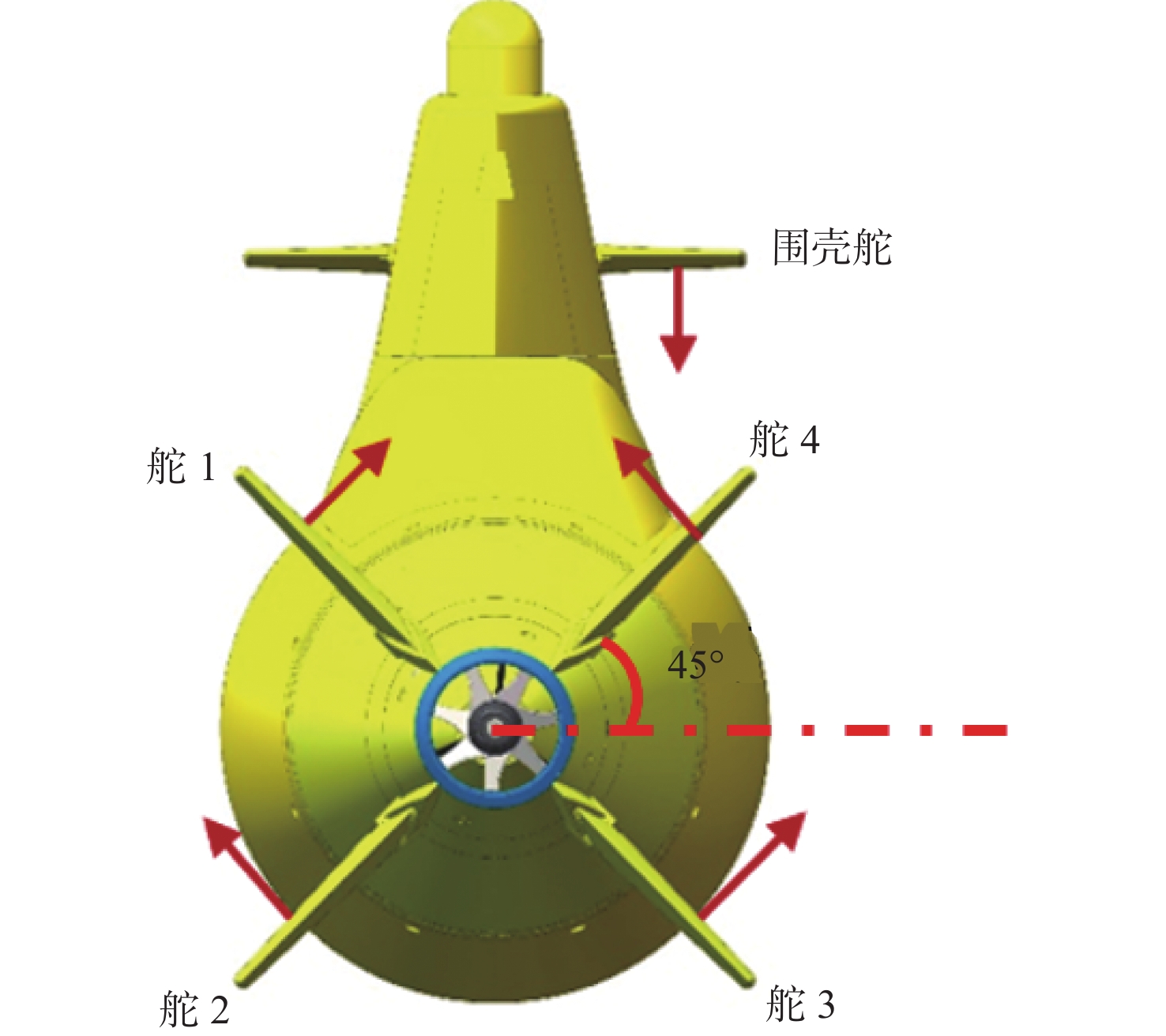
X舵与围壳舵的布局及对符号的规定如图4所示。图中，箭头所指的方向代表X舵与围壳舵的正向偏转方向，围壳舵的定义则遵循右手法则，以拇指指向右舷为正。从图4所示的布局图中可以看出，X舵的舵轴中心线与XAUV中线面之间的夹角为45°，形似“X”，且相邻两X舵之间的角度为90°，用于降低相邻舵之间的水动力扰动^[5]。

图  4  XAUV的舵布局

Figure  4.  Layout of XAUV's rudder

下载: 全尺寸图片 幻灯片

在本文研究中，XAUV的航向与深度调整主要是基于尾部所搭载的X舵进行，仅在必要时使用围壳舵进行深度控制。且由于XAUV围壳舵内部仅搭载有1个舵机，无法实现差动舵角，因此，本文研究不对围壳舵进行建模。

在XAUV执行任务的过程中，改变舵角便可以改变作用于水下航行器上的力和力矩。本文以${X_{\rm{r}}}$，${Y_{\rm{r}}}$，${Z_{\rm{r}}}$，${K_{\rm{r}}}$，${M_{\rm{r}}}$，${N_{\rm{r}}}$来表示水下航行器在运动过程中操纵X舵产生的各项舵力及力矩，其中${X_{\rm{r}}}$，${Y_{\rm{r}}}$，${Z_{\rm{r}}}$分别为作用于纵向、横向、垂向运动上的舵力，${K_{\rm{r}}}$，${M_{\rm{r}}}$，${N_{\rm{r}}}$分别为作用于横滚、纵倾、偏航运动上的舵力矩，具体表达式如式（1）所示。

式中： ${X}_{{{uu\delta}} _i}，{Y}_{{{uu\delta}} _i}，{Z}_{{{uu\delta}} _i}，{K}_{{{uu\delta}} _i}，{M}_{{{uu\delta}} _i}，{N}_{{{uu\delta}} _i}$ （i=1，2，3，4）为相应X舵的舵力系数；${\delta _i}$为第$i$ （i=1，2，3，4）个舵的操舵角。

由式（1）中${K_{\rm{r}}}$的表达式可知，当X舵的4个舵叶转动至合适的角度时，便会产生差动舵角从而产生横滚力矩，由此达到控制XAUV横滚运动的目的。X舵差动舵角${\delta _{{\rm{dr}}}}$的定义如下：

类似地，为了直观地体现X舵在深度与航向上的作用效果，将基于如下映射转换关系，把X舵4个舵叶的舵角变化转换为等效十字舵的舵效，转换公式如下：

式中：${\delta _{\rm{r}}}$代表等效十字舵的方向舵舵角；${\delta _{\rm{s}}}$代表等效十字舵的升降舵舵角。

1.4   XAUV数学模型

根据Prestero^[8]的工作，再结合XAUV自身的特点，本文为XAUV设计了运动学与动力学方程，分别如式（4）和式（5）所示：

式中：m_v为XAUV的质量，kg；$W$为XAUV的重量，N；$B$为XAUV的浮力；${x_{\rm{g}}}$，${y_{\rm{g}}}$，${{\textit{z}}_{\rm{g}}}$为XAUV重心的位置，m；${x_{\rm{b}}}$，${y_{\rm{b}}}$，${{\textit{z}}_{\rm{b}}}$为XAUV浮心的位置，m；形似${X_{(\dot * )}}$，${Y_{(\dot * )}}$，${Z_{(\dot * )}}$，${K_{(\dot * )}}$，${M_{(\dot * )}}$，${N_{(\dot * )}}$，${X_{( * * )}}$，${Y_{( * * )}}$，${Z_{( * * )}}$，${K_{( * * )}}$，${M_{( * * )}}$，${N_{( * * )}}$的参数均为XAUV水动力参数；${X_{\rm{T}}}$为推进器所产生的推力，N；${K_{\rm{T}}}$为推进器所产生的横滚力矩，N。

2.   横滚问题分析

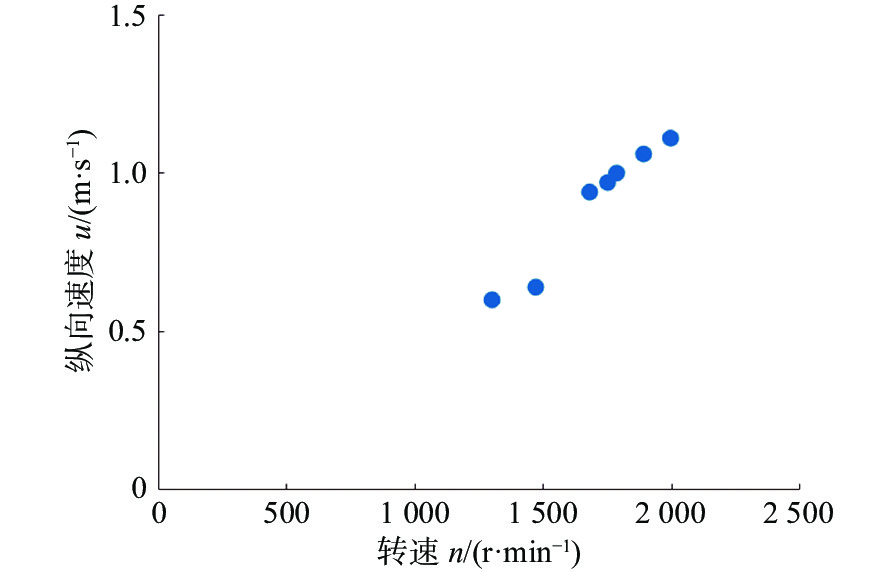
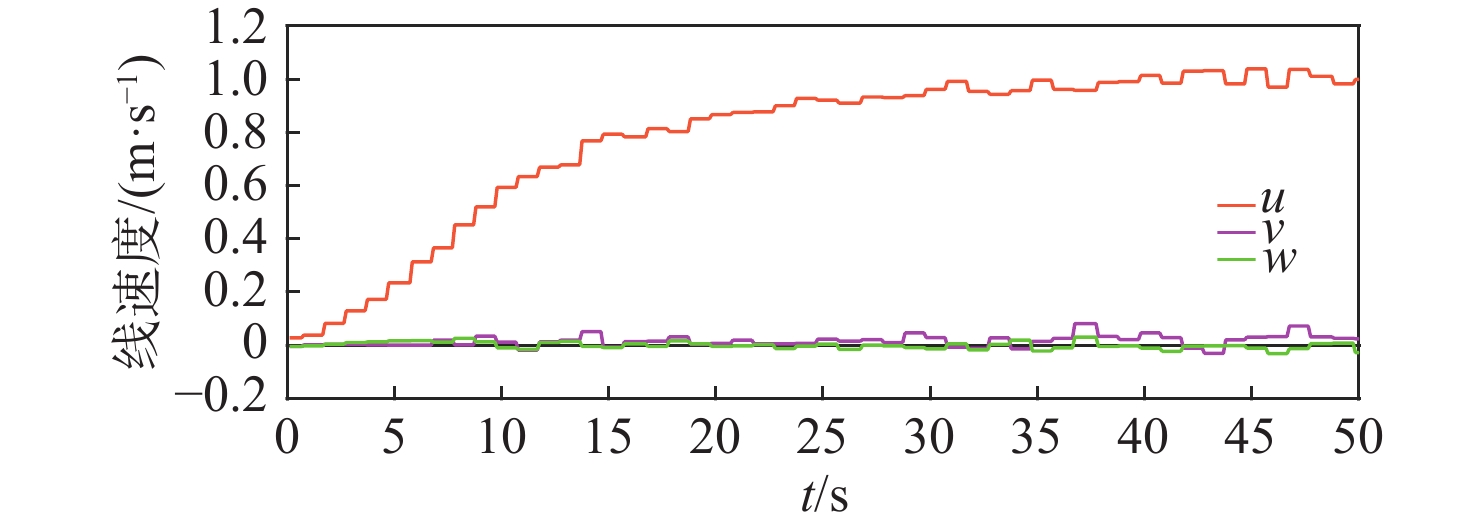
在XAUV的水池试验中，开展了多组水面定向直航试验，用以探索XAUV的快速性与推进器转速之间的关系，试验结果如图5所示。由图5可以发现，随着推进器转速的提高，XAUV的航速也相应提高。

图  5  XAUV在直航试验中转速n与纵向速度u的关系

Figure  5.  The relation between XAUV's propeller speed n and longitudinal velocity u in the heading fixed test

下载: 全尺寸图片 幻灯片

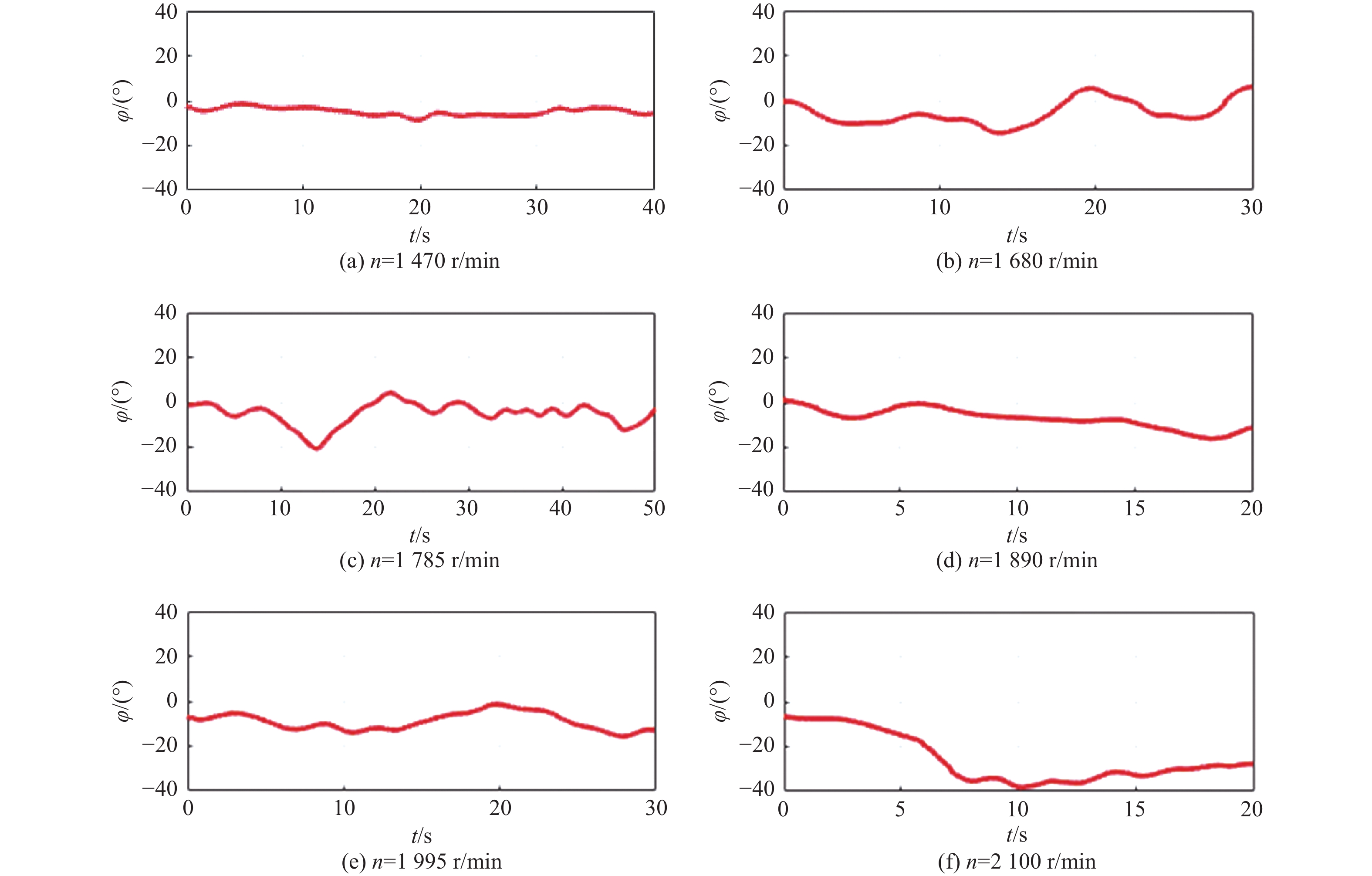
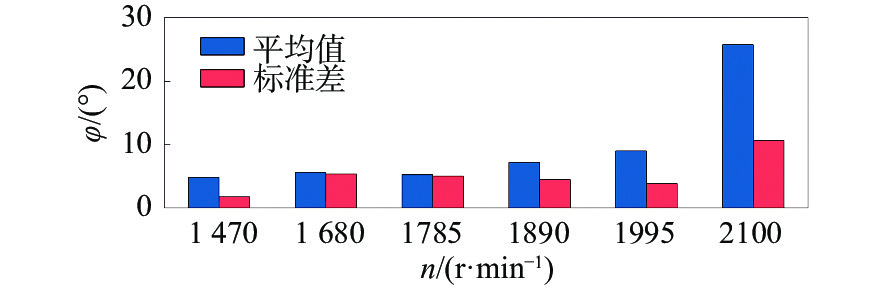
除此外，在系列定向直航试验中还发现，XAUV的横滚角随着转速的增加有着明显的提高，如图6与图7所示，当XAUV推进器的转速n=1 470 r/min时，XAUV的横滚角在10°范围以内变化，横滚角的平均值为4.86°；但当推进器的转速提高到2 100 r/min时，XAUV的横滚角超过了20°，横滚角的平均值已达到25.8°，且由于横滚角过大，改变了X舵的舵力，致使XAUV在水池中发生了失控事故。

图  6  XAUV在水面定向直航过程中的横滚角

Figure  6.  The roll angle of XAUV when moving through the water on the surface at fixed heading

下载: 全尺寸图片 幻灯片

图  7  XAUV在水面定向直航中横滚角的平均值与标准差

Figure  7.  The average value and standard deviation of roll angle when XAUV is moving through the water on the surface at fixed heading

下载: 全尺寸图片 幻灯片

结合推进器理论与XAUV的特性，总结出导致XAUV产生过大横滚角的原因如下。

1） 图8所示为XAUV所使用的推进器，该推进器为TECNADYNE公司所生产，型号为MODEL 300，由DC无刷电机驱动。螺旋桨式推进器的构成主要可分为转子与定子2个部分，其中转子的作用是带动水流运动从而产生使水下航行器运动的力，而定子的作用则主要是整流以及抵消转子所产生的横滚力矩^[9]。螺旋桨式推进器所产生的推力${X_{\rm{T}}}$与水下航行器前进的速度有关，公式如下：

式中：${K_{\rm{p}}}$为螺旋桨推力系数；$\rho$为液体密度，kg/m³；${D_{\rm{p}}}$为螺旋桨直径，m；${t_{\rm{p}}}$为推力减额系数。

图  8  X舵自主式水下航行器推进器示意图

Figure  8.  Schematic diagram of XAUV's thruster

下载: 全尺寸图片 幻灯片

在产生推力的同时，螺旋桨式推进器也会产生扭矩，扭矩值${K_{\rm{T}}}$的大小如下：

式中，${K_{\rm{Q}}}$为螺旋桨转矩系数。

2） 本文研究平台XAUV的艇宽B_w=300 mm。作为一艘小尺度的AUV，由于其内部元器件的布置以及其自身尺度的问题，XAUV的横稳性高仅为2 cm，自身横稳性不足，且由于在水面航行时XAUV的围壳部分并未浸入水中，致使XAUV的横稳性进一步降低。

3） 本文XAUV的试验场地为露天开放式操纵性水池，XAUV在水池中航行时会受到风、浪、流所产生的力与力矩的影响，故会对XAUV的运动产生影响。

3.   XAUV抗横滚水平面跟踪控制分析

3.1   面向横滚控制探索的开环差动舵横滚控制试验

为了克服XAUV在水平面内航行时的横滚问题，本文拟采用一种基于差动舵的控制理念抑制XAUV的横滚运动。首先，开展系列水面定向直航试验，探索差动舵角与推进器转速之间的关系，从而为XAUV的横滚控制器设计提供指导。

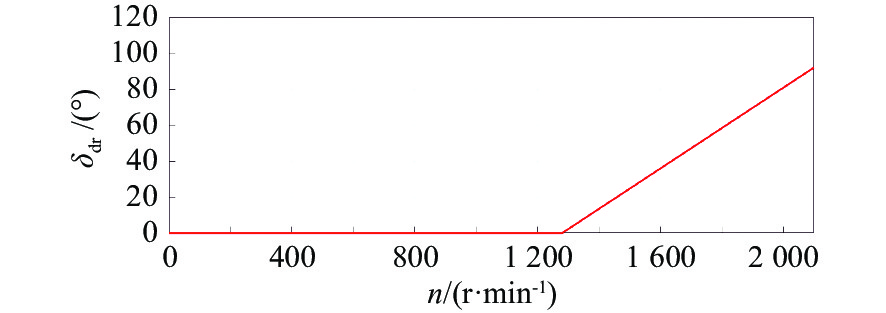
试验中，首先将XAUV推进器的转速分别设置为1 200，1 470，1 680，1 785，1 890，1 995和2 100 r/min，然后在固定转速的情况下，施加固定的差动舵角以对XAUV的横滚进行开环控制。当XAUV的横滚角变化范围在[−10°，10°]内时，即认为满足需求，进而可增大推进器转速以探索在下一转速情况下抑制横滚运动差动舵角的需求。根据上述试验方法，不同推进器转速情况下所对应的抗横滚差动舵角如表2所示。

表  2  横滚控制探索试验的试验结果

Table  2.  Results of roll control test

转速/(r·min−1)	差动舵角/(°)	舵效占比/%
1 200	0	0
1 470	32	26.7
1 680	48	40
1 785	56	46.7
1 890	76	63.3
1 995	84	70
2 100	92	76.7

下载: 导出CSV 

| 显示表格

为了直观地体现XAUV抗横滚差动舵角与推进器转速之间的关系，基于横滚控制探索试验结果，得到了如图9所示的XAUV在不同转速下抑制横滚运动的差动舵角图谱。该图谱的适用范围为XAUV的推进器转速在[0 r/min，2 100 r/min]时。从图9中可以看出，当XAUV推进器的转速大于1 680 r/min时，用于抑制横滚运动所需的差动舵角超过了48°，即超过40%的舵效都用于抑制XAUV的横滚运动，此时，大部分的舵效都被用来抑制横滚运动，导致剩余的舵效并不足以满足XAUV航向与深度精确控制的需求，而航向与速度控制是XAUV运动控制中的主旋律，因此在控制器设计环节应避免这种情况出现。所以，在设计水下航行器的运动控制器时，其最大转速应设置为1 680 r/min。

图  9  XAUV的转速与差动舵角关系图谱

Figure  9.  The relationship map of XAUV's propeller speed and differential rudder angle

下载: 全尺寸图片 幻灯片

3.2   XAUV抗横滚定深定向控制器设计

为了解决XAUV在航行过程中横滚角过大的问题，本文提出了如图10所示的运动控制方法。从图10中可以看出，本文所提的运动控制方法可以分为动力学控制器与控制器分配器2个部分。其中，动力学控制器又可以分为2个部分：第1部分为基于反馈线性化PD控制的横滚与航向控制器；第2部分则是基于增量反馈控制的深度控制器。首先，将期望横滚角${\varphi _{\rm{d}}}$、航向角${\psi _{\rm{d}}}$、深度值${{\textit{z}}_{\rm{d}}}$与XAUV真实状态所反馈的横滚角$\varphi$、航向角$\psi$、深度值${\textit{z}}$之间的差值${e_{\varphi} }$，${e_\psi }$，${e_{\textit{z}}}$作为动力学控制器的输入，其中${e_{\varphi }}$和${e_\psi }$经过反馈线性化PD控制器的计算输出期望横滚力矩${\tau _{p{\rm{d}}}}$与偏航力矩${\tau _{r{\rm{d}}}}$，${e_{\textit{z}}}$则通过增量反馈控制器计算输出纵倾力矩增量$\Delta {\tau _{q{\rm{d}}}}$，经累加器计算得出期望纵倾力矩${\tau _{q{\rm{d}}}}$。在增量反馈控制器的计算中，${e_\theta }$代表期望纵倾角${\theta _{\rm{d}}}$与XAUV当前纵倾角$\theta$的误差，${e_q}$代表期望纵倾角速度${q_{\rm{d}}}$与XAUV当前纵倾角速度$q$的误差，${e_{\dot q}}$代表期望纵倾角加速度${\dot q_{\rm{d}}}$与XAUV当前纵倾角加速度$\dot q$的误差。之后，基于动力学控制器所输出的期望横滚力矩${\tau _{p{\rm{d}}}}$、偏航力矩${\tau _{r{\rm{d}}}}$与纵倾力矩${\tau _{q{\rm{d}}}}$进行约束非线性规划，便可解算得到XAUV四个舵角的输入${\delta _1}$，${\delta _2}$，${\delta _3}$，${\delta _4}$，进而实现在控制XAUV航向与深度的同时达到抑制横滚角的目的。

图  10  X舵水下航行器的抗横滚运动控制器框图

Figure  10.  The anti-roll motion controller's framework of XAUV

下载: 全尺寸图片 幻灯片

3.2.1   基于反馈线性化PD控制的横滚与航向控制器设计

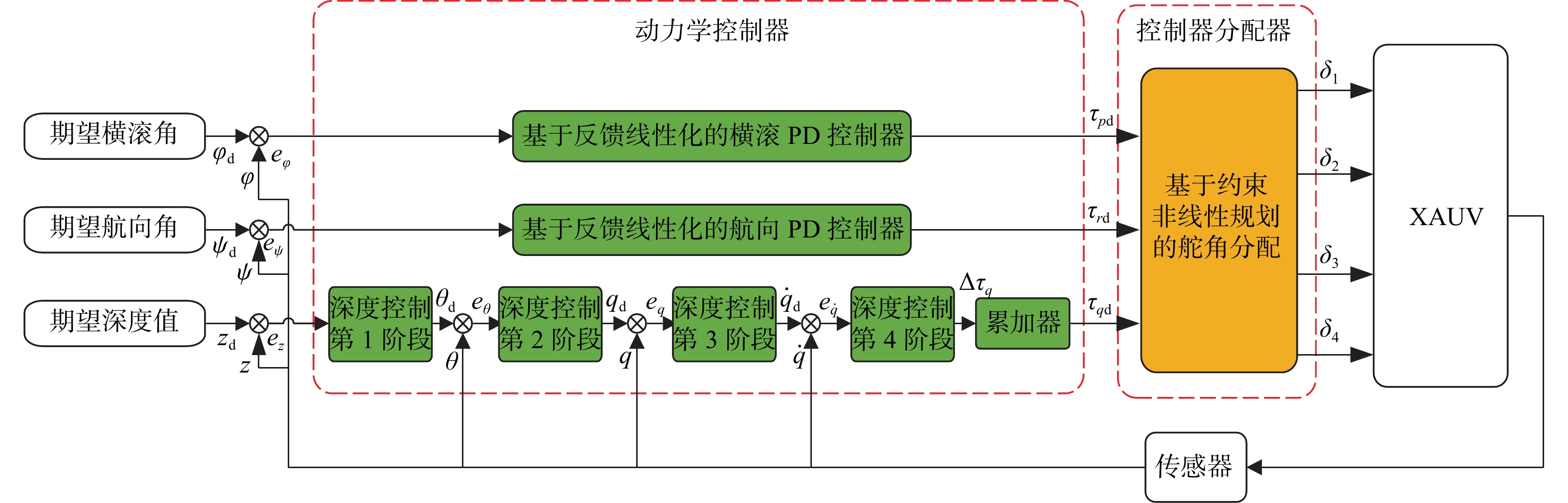
结合式（4）和式（5），XAUV在横滚与偏航方向上的动力学方程可以写成如下仿射非线性形式：

式中：${\tau _p}$代表作用于横滚运动上的横滚力矩，${\tau _r}$代表作用于偏航运动上的偏航力矩，${f_p}$，${g_p}$，${f_r}$，${g_r}$的具体表达式如下：

对于形式类似${x^{(i)}} = f + gu$的第i阶非线性系统，可设计形式如$u = ( - f + x_{\rm{d}}^{(i)} + {K^{\rm{T}}}e)/g$的反馈线性化控制器，用以在$f$和$g$预知的情况下消除系统的非线性。因此根据式（8），可将XAUV的控制输入设计为如下形式：

式中：${\ddot \varphi _{\rm{d}}}$，${\ddot \psi _{\rm{d}}}$分别代表期望横滚角与偏航角的二阶导数值；${K_{{\rm{D}}\varphi }}$，${K_{{\rm{D}}\psi }}$分别代表横滚与航向PD控制器中微分环节的增益参数；${K_{{\rm{P}}\varphi }}$，${K_{{\rm{P}}\psi }}$则分别代表横滚与航向PD控制器中比例环节的增益参数；${\dot e_{\varphi }}$，${\dot e_\psi }$为${e_{\varphi }}$和${e_\psi }$的一阶导数值，${e_{\varphi }}$，${e_\psi }$的具体定义如下：

结合式（8）与式（10），可以得到

根据式（12），可以将XAUV闭环控制系统的相应特征方程写为式（13）所示的形式，其中s为由式（12）推导出的特征方程的参数。

由Routh-Hurwitz判据，可知当${K_{{\rm{D}}\varphi }} > 0$，${K_{{\rm{D}}\psi }} > 0$，${K_{{\rm{P}}\varphi }} > 0$，${K_{{\rm{P}}\psi }} > 0$时，上述特征方程的根将全都位于复平面的左半区。因此，当时间$t \to \infty$时，误差$e(t)$与误差变化率$\dot e(t)$都将趋近于0，由此XAUV的横滚角与偏航角最终都将收敛至期望值。相比传统的PD控制需要借助反步法的帮助才能进一步推导${\tau _{p{\rm{d}}}}$与${\tau _{r{\rm{d}}}}$的表达式并构造复杂的Lyapunov函数来证明控制系统的稳定性，本文所采用的反馈线性化PD控制技术不仅简化了${\tau _{p{\rm{d}}}}$与${\tau _{r{\rm{d}}}}$的推导过程，同时也降低了系统稳定性证明的复杂程度，实用且高效。

3.2.2   基于增量反馈控制的深度控制器设计

基于增量反馈控制的深度控制器原理图如图10所示。深度控制回路中包含有4个阶段，可将XAUV当前深度与期望深度的插值作为控制输入，并将纵倾力矩增量作为控制输出，随后在累加器的帮助下获得期望纵倾力矩的值，具体的推导过程如下。

首先，对双环增量反馈控制中不同计算阶段的误差进行定义。

定义完误差之后，设计如下增量控制律：

式中：${k_i}$(i=1，2，3，4)为控制增益；${\varDelta _i}$(i=1，2，3，4)为每个控制循环中的比例因子；$\Delta {\tau _q}$为纵倾力矩${\tau _q}$的增量。$\tanh$作为一个连续、平滑且饱和的函数，在控制循环周期中引入$\tanh$可以在输入误差接近零点时获得接近指数收敛的速率，而当输入误差远离零点时，以固定速率收敛，且$\tanh$的引入可限制期望纵倾速率和期望纵倾加速度等，从而避免出现突变情况。

最后，t时刻的期望纵倾力矩指令可通过下式获得。

基于增量反馈控制的深度控制器的稳定性证明可分为如下4个步骤。

1） 对${e_{\dot q}}$的收敛性进行证明。定义Lyapunov函数${V_1}$为

将式（17）进行微分，并代入式（15）与式（16），得到

由于$\dfrac{{\partial {e_{\dot q}}}}{{\partial {\tau _q}}} = \dfrac{{\partial ({{\dot q}_d} - q)}}{{\partial {\tau _q}}} = - \dfrac{{\partial \dot q}}{{\partial {\tau _q}}} < 0$，因此${\dot V_1} \leqslant 0$，并且当且仅当${e_{\dot q}} = 0$时${\dot V_1} = 0$。至此，${e_{\dot q}}$的收敛性证明完毕。

2） 对${e_q}$的收敛性进行证明。定义Lyapunov函数${V_2}$为

将式（19）进行微分，由于${e_{\dot q}}$的收敛性已证明完毕，因此可代入$\dot q = {k_3}\tanh ({e_q}/{\varDelta _3})$，获得如下公式：

由于$\dfrac{{\partial {e_q}}}{{\partial q}} = \dfrac{{\partial ({q_d} - q)}}{{\partial q}} < 0$，因此${\dot V_2} \leqslant 0$，并且当且仅当${e_q} = 0$时${\dot V_2} = 0$。至此，${e_q}$的收敛性证明完毕。

3） 对${e_\theta }$的收敛性进行证明。定义Lyapunov函数${V_3}$为

将式（21）进行微分，由于${e_q}$的收敛性已证明完毕，因此可代入$q = {k_2}\tanh ({e_\theta }/{\varDelta _2})$，获得如下公式：

由于$\dfrac{{\partial {e_\theta }}}{{\partial \theta }} = \dfrac{{\partial ({\theta _d} - \theta )}}{{\partial \theta }} < 0$，因此${\dot V_3} \leqslant 0$，并且当且仅当${e_\theta } = 0$时${\dot V_3} = 0$。至此，${e_\theta }$的收敛性证明完毕。

4） 对${e_{\textit{z}}}$的收敛性进行证明。定义Lyapunov函数${V_4}$为

将式（24）进行微分，由于${e_\theta }$的收敛性已证明完毕，因此可代入$\theta = {k_1}\tanh ({e_{\textit{z}}}/{\varDelta _1})$，获得如下公式：

由于$\dfrac{{\partial {e_{\textit{z}}}}}{{\partial {\textit{z}}}} = \dfrac{{\partial ({{\textit{z}}_d} - {\textit{z}})}}{{\partial {\textit{z}}}} < 0$，因此${\dot V_4} \leqslant 0$，并且当且仅当${e_{\textit{z}}} = 0$时${\dot V_4} = 0$。至此，${e_{\textit{z}}}$的收敛性证明完毕。

综上，基于增量反馈控制的深度控制器的稳定性证明完毕。

3.2.3   基于序列二次规划算法的舵角分配

在动力学控制器输出期望横滚力矩、期望纵倾力矩与期望偏航力矩之后，控制器分配器就会根据动力学控制器的输出结果对实际舵角进行解算。作为一个典型的单输入多输出（single input-multioutput，SIMO）问题，其解并不唯一，该多目标优化问题的数学表达式如式（25）所示。

式中：J为基于最小舵力矩误差与最小控制影响理念而定义的惩罚函数；J中权重因子$\zeta$的作用为平衡误差与控制输入之间的关系；${\boldsymbol{\delta }}$为由X舵的4个舵角${\delta _1}$，${\delta _2}$，${\delta _3}$，${\delta _4}$所组成的舵角向量；$erro{r_p}$，$erro{r_q}$，$erro{r_r}$分别为当前横滚、纵倾、偏航舵力矩与期望横滚、纵倾、偏航舵力矩之间的差值； ${\tau _{p{\rm{d}}}}$，${\tau _{q{\rm{d}}}}$，${\tau _{r{\rm{d}}}}$分别为由动力学控制器输出的期望横滚力矩、期望纵倾力矩与期望偏航力矩；${\boldsymbol{error}}_{\rm{t}}$为由$erro{r_p}$，$erro{r_q}$，$erro{r_r}$三者组成的误差向量。除此外，在定义多目标优化问题的数学表达式时，考虑到舵机的实际特性，舵角的输出范围被限制为[−30°，30°]。

为解决该多目标优化问题，本文采用了序列二次规划（sequential quadratic programming，SQP）算法。该算法是一种由Boggs于1996年提出的求解约束优化问题的有效算法，其主要迭代过程如下：

1） 选择优化变量${\vartheta _0}$与海森矩阵${{\boldsymbol{H}}_0}$的初始状态；

2） 求解二次规划（quadratic programming，QP）子问题，从而获得搜索方向${d_i}$；

3） 基于搜索方向${d_i}$更新优化变量${\vartheta _i}$与海森矩阵${{\boldsymbol{H}}_i}$；

4） 以拉格朗日函数${L_i}$的形式计算目标函数；

5） 判断代价函数${J_i}$是否收敛，如果收敛，则结束迭代，否则，重复第2）~5）步；

6） 结束迭代。

4.   水池试验

4.1   X舵水平面操纵性能验证试验

众所周知，X舵的性能要优于传统十字舵，但当前的研究大多停留在定性分析层面。为了定量对比验证X舵相比十字舵在性能上的优势，本文借助XAUV艉舵构型可变换的特点（图11），通过在操纵性水池中开展定深定速回转试验与Z形操舵试验，对2种不同艉舵构型的特性进行了分析。

图  11  XAUV艉舵构型变换示意图

Figure  11.  Schematic diagram of rudder configuration transformation for XAUV

下载: 全尺寸图片 幻灯片

进行定深定速回转试验的目的是对比2种不同艉舵构型AUV的回转性能。在试验中，设定航速为2 kn，深度为1.5 m，方向舵舵角分15°和20°两种不同的工况，试验过程如图12所示。

图  12  定深回转试验

Figure  12.  Depth fixed turning test

下载: 全尺寸图片 幻灯片

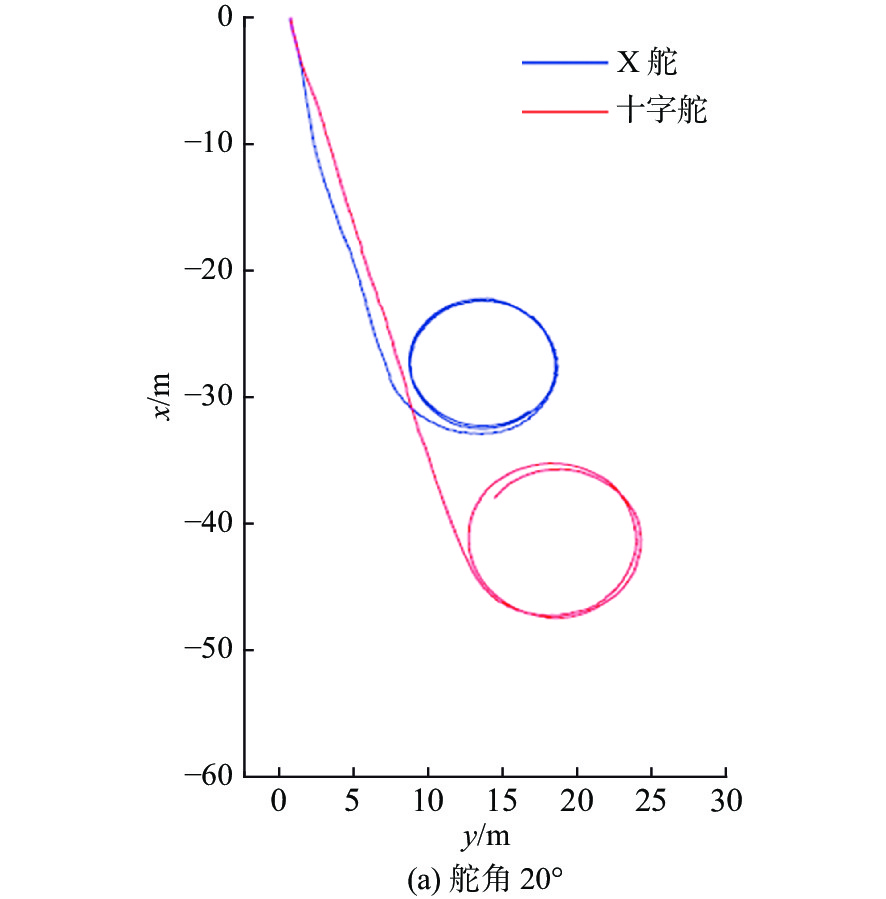
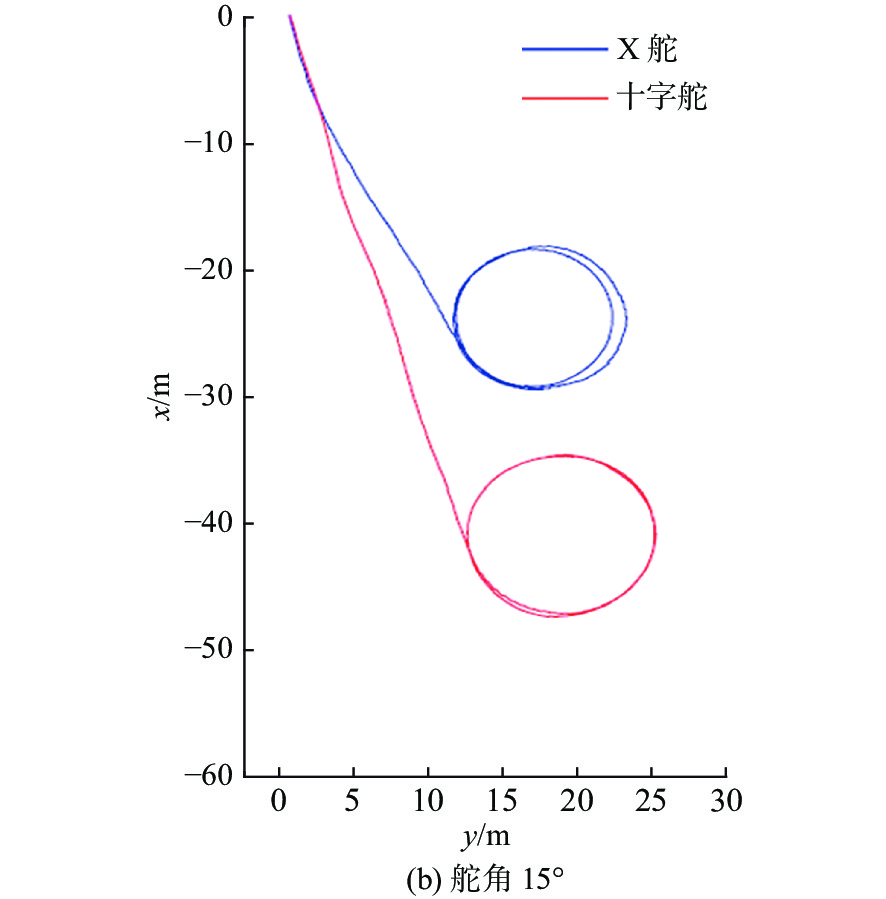
定深定速回转试验的试验结果如图13所示。通过对试验结果进行定性分析，显示无论是15°还是20°的方向舵舵角，X舵水下航行器的回转半径均小于十字舵水下航行器的回转半径。表3给出了定深定速回转试验的定量分析结果。结果显示在相同艇体模型下，十字舵水下航行器的回转半径约为X舵水下航行器的1.2倍。

下载: 全尺寸图片 幻灯片

表  3  定深回转试验定量分析结果

Table  3.  Quantitative analysis results of depth fixed turning test

舵角/(°)	X舵回转直径/m	十字舵回转直径/m	比值
15	13.5	11.2	1.21
20	12.9	10.3	1.25

下载: 导出CSV 

| 显示表格

图  13  定深回转试验结果

Figure  13.  The results of depth fixed turning test

下载: 全尺寸图片 幻灯片

进行Z形操舵试验的目的是对比X舵与十字舵水下航行器的应舵性能。在试验中，设定航速为2 kn，方向舵舵角分10°与20°两种工况，试验过程如图14所示。

图  14  Z形操舵试验

Figure  14.  Zigzag maneuver test

下载: 全尺寸图片 幻灯片

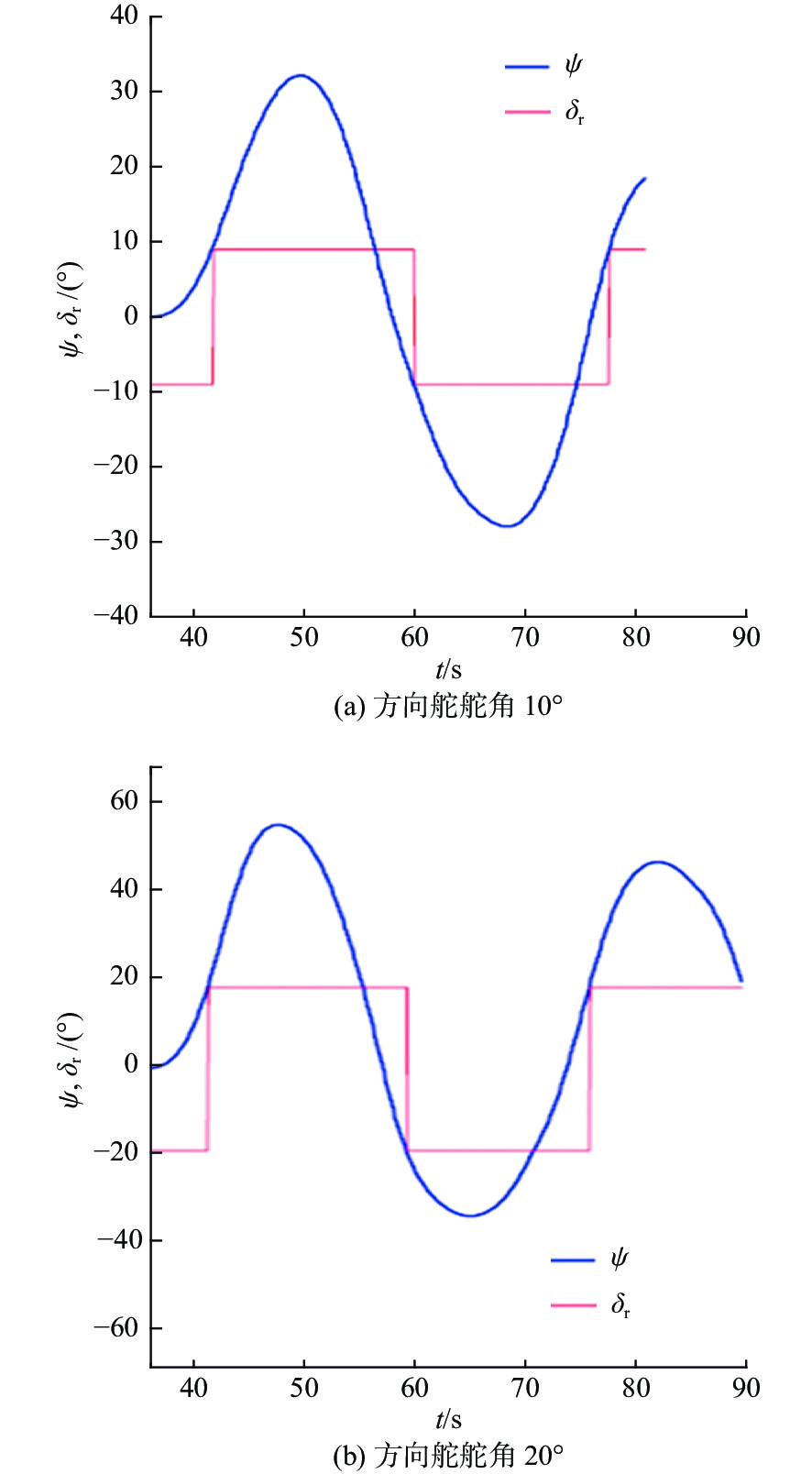
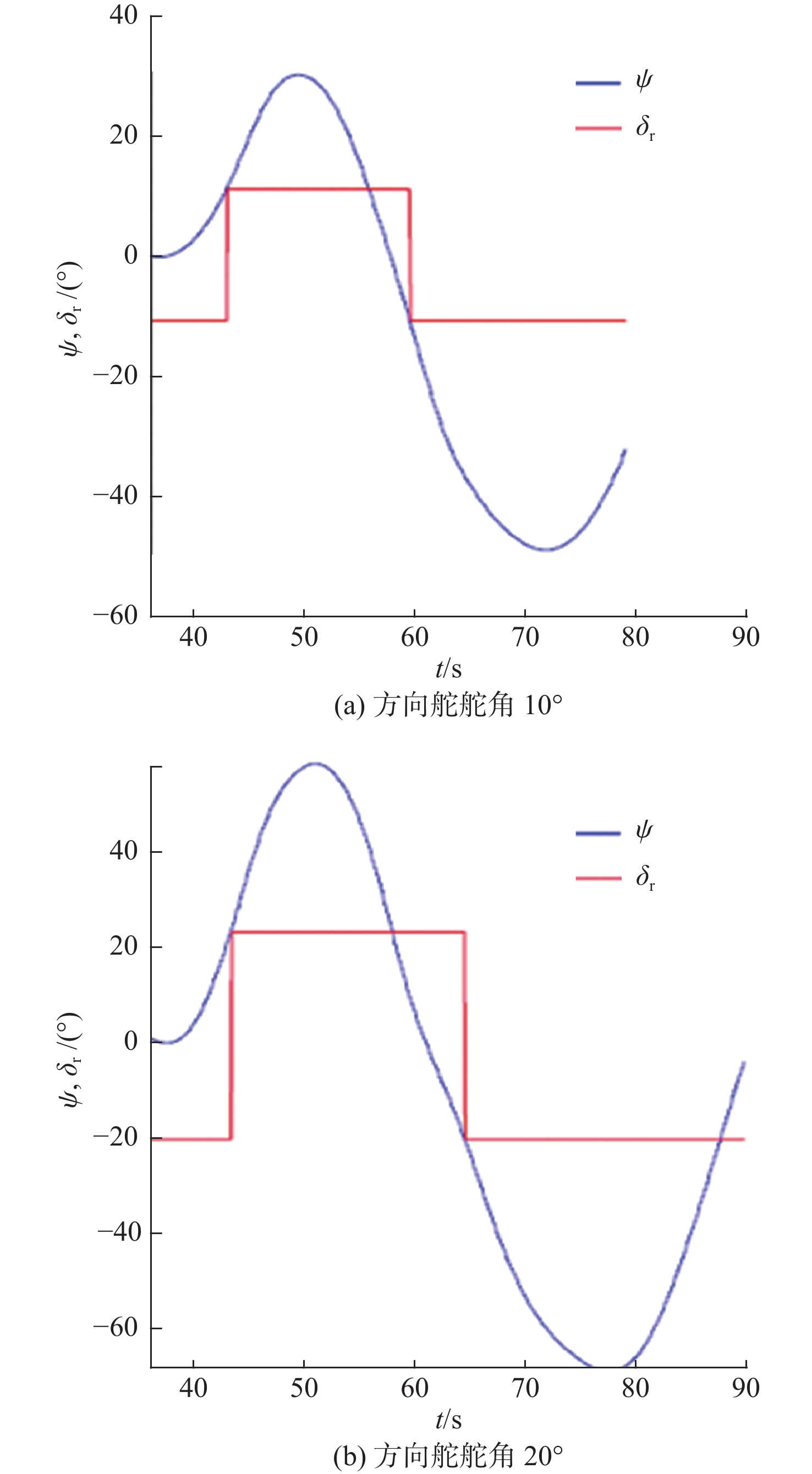
Z形操舵试验的试验结果如图15、图16所示。通过对试验结果进行定性分析，显示X舵水下航行器对比十字舵水下航行器具有更大的超越艏向角，但艏向角超越时间和全周期时间更短。表4所示为Z形操舵试验定量分析结果。结果显示在相同的艇体模型下，X舵水下航行器相比十字舵水下舵行器具有更大的回转性指数K和更小的稳定性指数T，因而具有更优的回转性能。此外，回转性指数K的比值（${K_{\rm{X}}}/{K_{\text{ + }}}$）约为1.2，稳定性指数T的比值（${T_{\rm{X}}}/{T_{\text{ + }}}$）约为0.77，其中${K_{\rm{X}}}$，${T_{\rm{X}}}$分别为X舵模式下的回转性指数与稳定性指数，${K_{\text{ + }}}$，${T_{\text{ + }}}$分别为十字舵模式下的回转性指数与稳定性指数。

图  15  X舵自主式水下航行器的Z形操舵试验结果

Figure  15.  Results of XAUV's zigzag maneuver test

下载: 全尺寸图片 幻灯片

图  16  十字舵水下航行器的Z形操舵试验结果

Figure  16.  Results of cruciform rudder autonomous underwater vehicle's zigzag maneuver test

下载: 全尺寸图片 幻灯片

表  4  Z形操舵试验定量分析结果

Table  4.  Quantitative analysis results of zigzag maneuver test

参数	X舵(10°)	X舵(20°)	十字舵(10°)	十字舵(20°)
稳定性指数T	0.35	0.29	0.47	0.37
回转性指数K	0.43	0.35	0.38	0.3

下载: 导出CSV 

| 显示表格

综合考虑回转试验与Z形操舵试验的定性、定量分析结果，可知在相同艇体模型下，相比十字舵，X舵的回转性能更好，因此针对特殊的任务需求，可以换装X舵来提高水下航行器的操纵性以满足任务需求。

4.2   近水面抗横滚定深定向控制试验

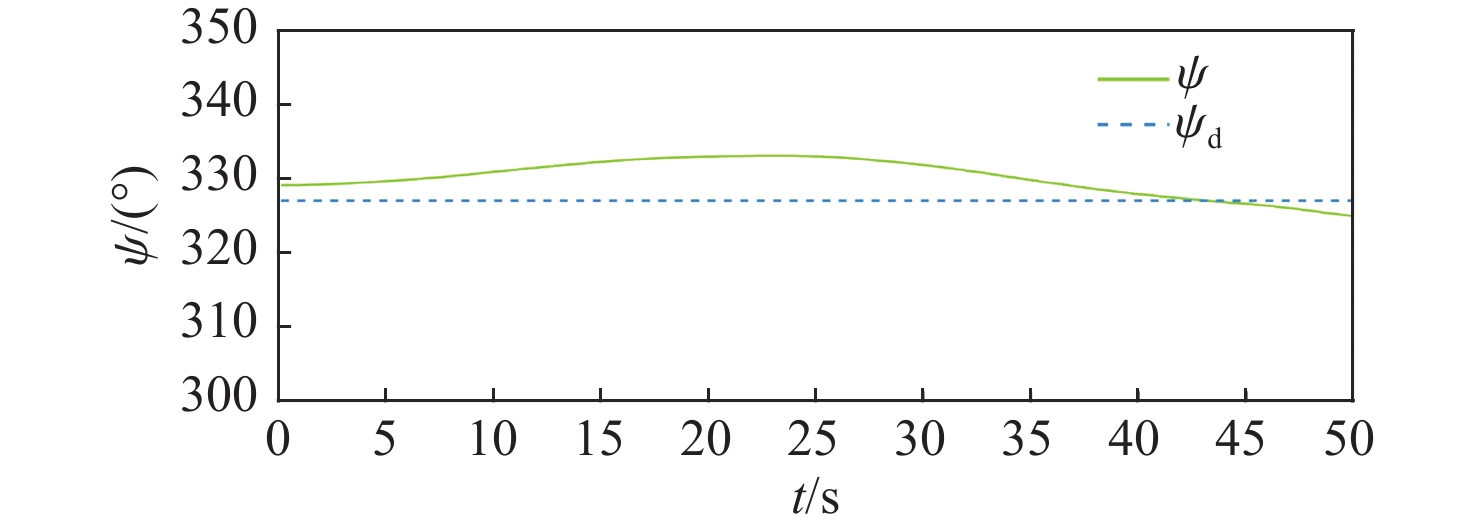
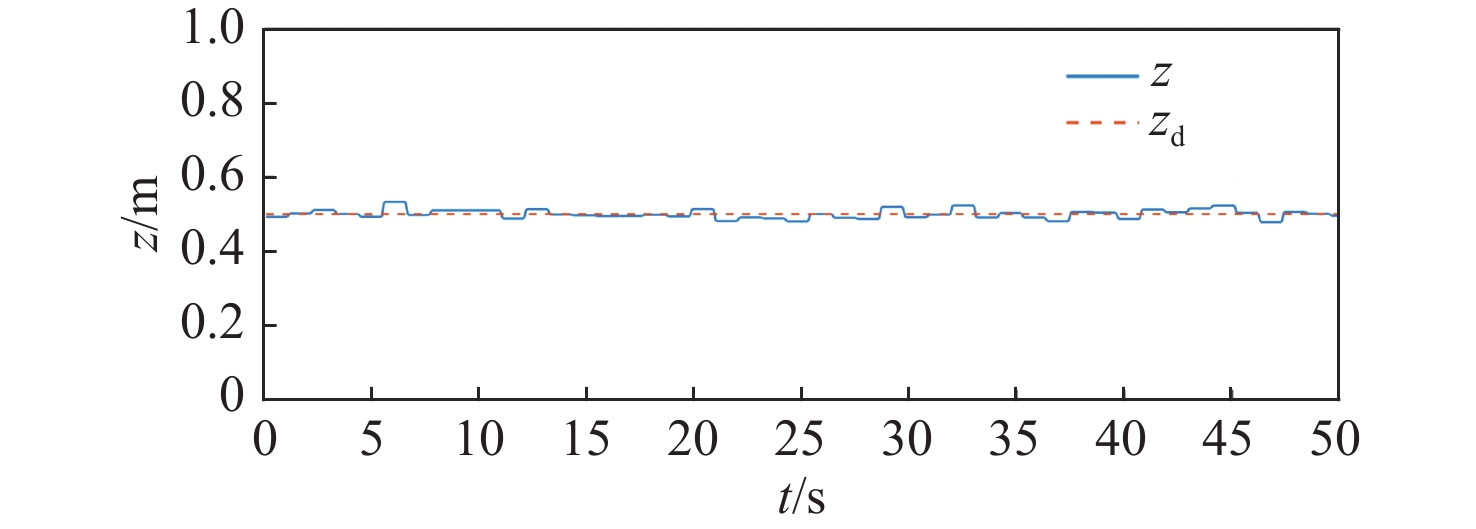
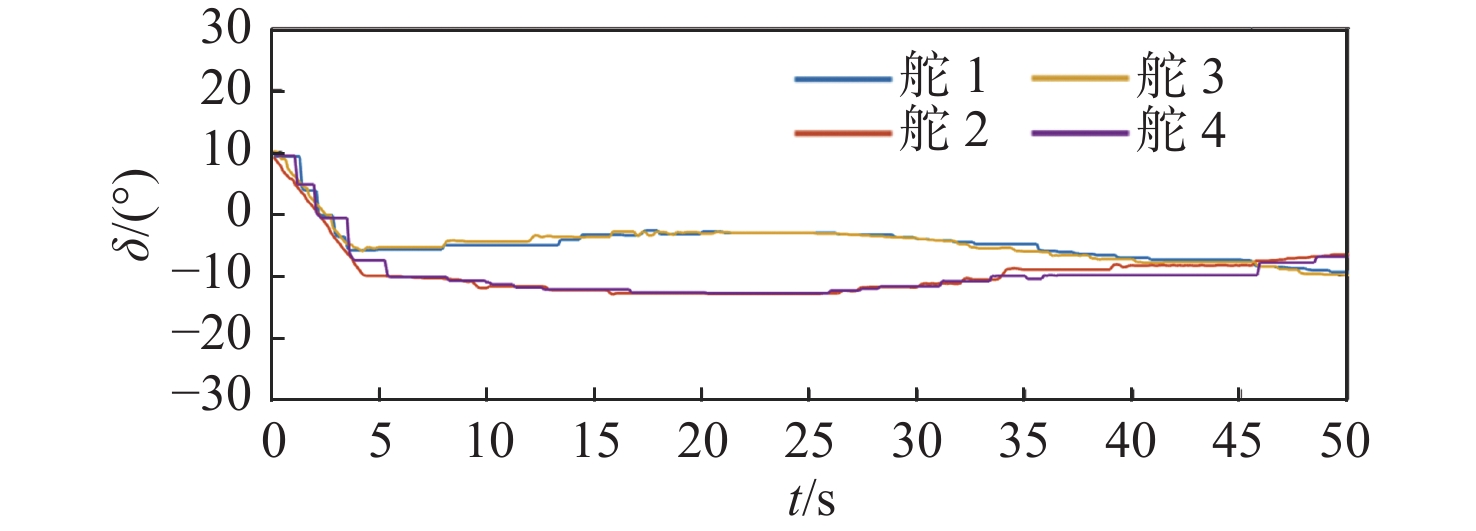
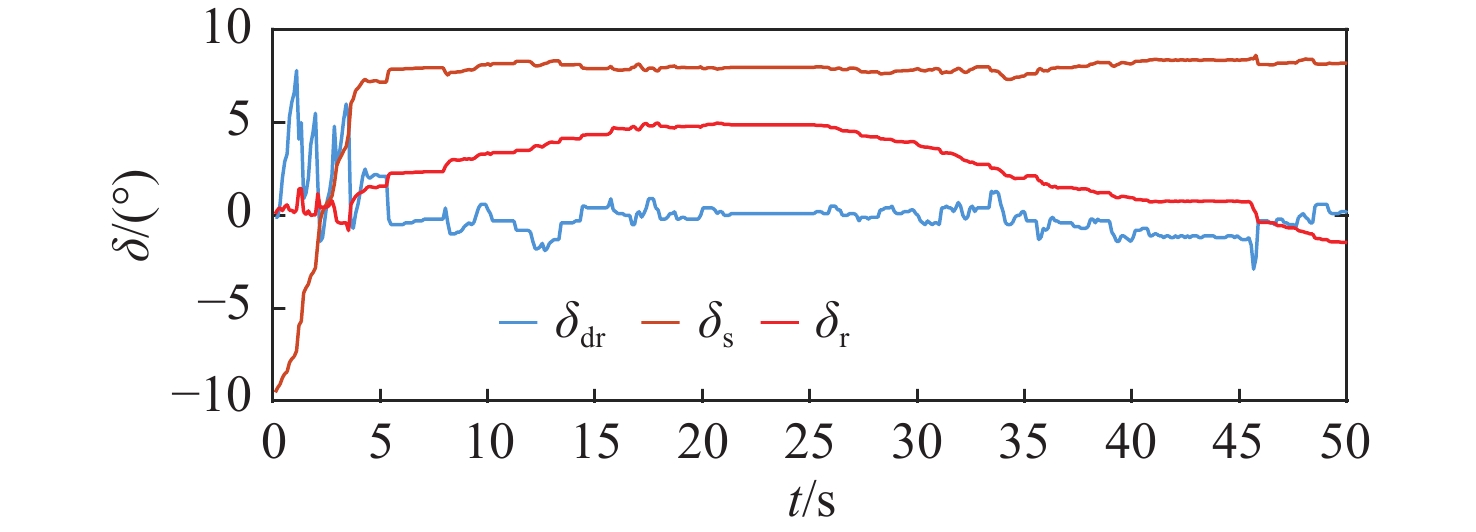
为了验证本文所提控制器的性能，在60 m×60 m×5 m（长×宽×深）的操纵性水池中基于XAUV进行了近水面定深定向控制试验，试验结果如图17~图22所示。由XAUV水面定向试验与水面开环差动舵摸索试验的结果可知，当XAUV推进器的转速n>1 680 r/min且围壳部分露出水面时，抑制XAUV横滚运动所需的差动舵角占据了总舵效的40%以上，剩余舵效不足以满足XAUV航向控制与深度控制的精度需求。因此，在本次试验中将XAUV的转速设置为1 680 r/min，同时通过调整浮力的方法将XAUV的初始深度设置为0.5 m，并将围壳部分浸没于水中，以增加XAUV的横稳性。

图  17  XAUV在试验中的线速度

Figure  17.  The linear velocity of XAUV during the field test

下载: 全尺寸图片 幻灯片

图  18  XAUV在试验中的横滚角

Figure  18.  The roll angle of XAUV during the field test

下载: 全尺寸图片 幻灯片

图  19  XAUV在试验中的航向角

Figure  19.  The heading angle of XAUV during the field test

下载: 全尺寸图片 幻灯片

图  20  XAUV在试验中的深度

Figure  20.  The depth of XAUV during the field test

下载: 全尺寸图片 幻灯片

图  21  XAUV在试验过程中的舵角控制输入

Figure  21.  The actuator's control inputs during the field test

下载: 全尺寸图片 幻灯片

图  22  基于映射关系的简化X舵舵角控制输入显示

Figure  22.  Simplified X-rudder's control input based on the mapping translation

下载: 全尺寸图片 幻灯片

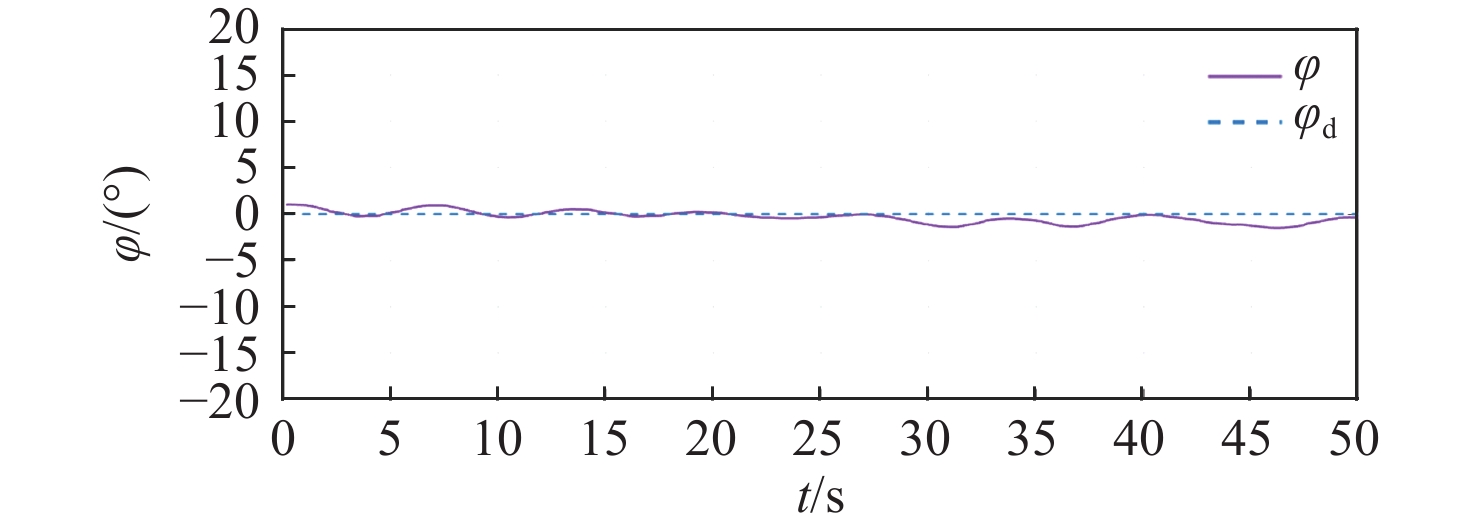
由图17~图22所示的XAUV在近水面定深定向试验中所得的横滚角、航向角以及深度变化结果可以看出，采用本文所提控制方法可使XAUV在既定航向、深度运行时能有效抑制XAUV的横滚角。从横滚控制的角度来看，并结合图18所示的XAUV在运动过程中的横滚角变化可知，增加横滚控制项并将围壳部分浸没于水中的做法可有效降低横滚角对航向与深度控制的影响，XAUV的横滚角始终控制在2°的变化范围内，且XAUV的横滚角变换平缓，能有效避免因横滚角突变而带来的意外。从航向控制的角度来看，并结合图19所示的XAUV在运动过程中的航向角变化可知，在定深定向航向过程中，XAUV能较好地保持既定航向，虽然在航行过程中XAUV的航向角与期望航向角间的最大偏差为6.03°，但这是因为在XAUV的起步阶段纵向速度u较小，由式（1）可知，此时X舵的舵效率较低，因而在航向控制上略显不足，但从总体上来看，在试验期间，XAUV的航向能保持在既定的航向上，可满足控制需求。从深度控制的角度上看，并结合图20所示的XAUV在运动过程中的深度变化可知，在定深定向航向过程中，XAUV能较好地保持既定深度，即使在整体试验过程中当XAUV的深度在0.5 m附近有着一定的波动时，XAUV的深度与期望深度间的最大偏差也仅为3.2 cm（t = 6 s），综合考虑近水面航行过程中XAUV受到的波浪与流的影响以及XAUV在起步阶段的不稳定性，可知在试验期间XAUV的深度能保持在既定的深度上，满足控制需求。

综合考虑XAUV在水池试验中的横滚控制、航向控制与深度控制结果，可以得到如下结论：基于本文所提的考虑了横滚动力学的水下航行器深度与航向控制方法，可在近水平面定深定向任务中有效抑制XAUV的横滚运动并实现航向与深度的高精度控制，这表明在XAUV控制器的设计中，应对横滚动力学加以考虑，以发挥X舵的特定优势并提高水下航行器的控制精度。

值得说明的是，本次基于XAUV所进行的抗横滚定深定向控制试验是在封闭的操纵性水池中进行的，相比真实的海中或湖泊中应用场景，XAUV受到的风、浪、流影响较小，无法还原XAUV在实际应用场景中受到的横滚扰动，实验结果具有一定的局限性。因此，在后续野外现场试验中，还将进一步对XAUV的抗横滚控制进行深入研究，探索扰动观测器在抗横滚控制中的应用，从而降低外界扰动对XAUV横滚的影响，提高AUV的控制精度。

5.   结　语

本文针对XAUV在航行中的横滚问题，提出了一种考虑了横滚动力学的抗横滚近水面定深定向控制策略，并借助XAUV艉舵构型可转换的特点，定量分析了X舵相比十字舵在操纵性上的优势。在设计XAUV运动控制器之前，首先开展了开环差动舵横滚控制试验并进行了摸索；之后，参考水池试验结果并针对XAUV的近水面定深定向任务设计了近水面抗横滚定深定向控制器，其基于模型，通过参考反馈线性PD控制器与增量反馈控制器输出了期望偏航、纵倾与横滚力矩；随后，通过SQP算法求解约束非线性规划问题得到了X舵的舵角输入信号，从而达到了控制XAUV航向、深度与横滚角的目的。水池试验的结果验证了本文提控制方法的有效性与X舵的优越性，显示在相同的艇体模型下，常规十字舵的回转直径为本文所设计X舵的1.2倍，且基于本文所提控制方法，可将XAUV的横滚角在推进器转速为1 680 r/min时有效抑制在2°以内，这样不仅可抑制XAUV的横滚运动，也可使XAUV具有良好的航向与深度保持能力。

与常规的水下航行器相比，X舵水下航行器具有明显的操纵性优势以及容错性能。本文仅针对XAUV的操纵性及抗横滚控制进行了初步研究，为进一步探索XAUV的特性并充分发挥其优势，未来，还将开展以下几方面的研究：

1） 探索模型预测控制（model predictive control，MPC）在XAUV中的应用，降低XAUV的操舵频率，借此提高AUV的续航能力，并改善AUV的隐身能力。

2） 探索容错控制在（fault tolerant control，FTC）在XAUV中的应用，以保障并提高XAUV在舵机故障状态下的生存能力与操纵性，深度挖掘X舵的安全性能优势。