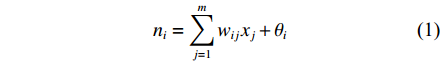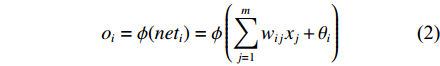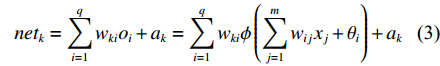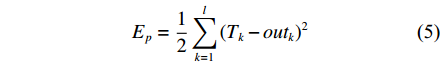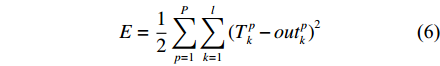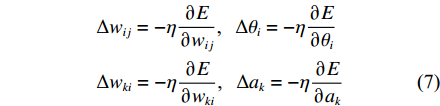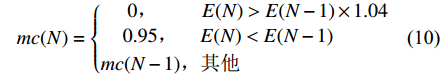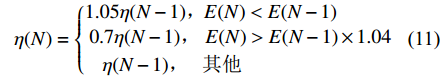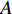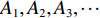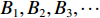Fault diagnosis of ship power system based on optimized BP neural network
-
摘要:目的 为实现船舶动力系统的故障诊断,基于优化的BP神经网络提出一种故障诊断方法。方法 首先,采用附加动量−自适应学习速率调整算法来克服BP神经网络的缺陷;然后,运用“小网络集群”的思路分别构建网络以进行故障识别和故障溯源;接着,采用动力系统仿真平台生成的450组故障数据进行神经网络训练;最后,通过给水泵转速异常高这一故障案例展示故障诊断结果。结果 通过对故障数据的学习,发现故障原因诊断准确率可高达99%以上。结论 研究表明,基于优化BP神经网络的故障诊断方法能够精准实现船舶动力系统的故障诊断。Abstract:Objectives In order to realize the fault diagnosis of a ship power system, this paper proposes a fault diagnosis method based on an optimized back-propagation (BP) neural network.Methods First, a momentum/adaptive learning rate adjustment algorithm is used to overcome the defects of the BP neural network. The idea of a "small network cluster" is then adopted to construct a separate network for fault identification and diagnosis. Next, 450 groups of fault data generated from a ship power system simulation platform are used for neural network training. Finally, the fault diagnosis results are demonstrated via a fault case in which the speed of a feed water pump is abnormal.Results Through training in fault data, the fault diagnosis accuracy level reaches more than 99%.Conclusions The proposed fault diagnosis method based on an optimized BP neural network can accurately realize the fault diagnosis of ship power systems.
-
0. 引 言
船舶动力系统结构复杂,子系统和设备众多,并且各子系统还具有强耦合性和非线性的特点。当系统出现故障时,如果仅依靠操作人员的经验判断,往往难以快速定位故障原因,从而可能延误排除故障的最佳时机,导致故障严重程度升级,造成船舶的机动性和操控性受损,进而威胁航行安全。因此,在动力系统发生故障时,准确定位故障设备,快速分析出故障原因对于保障航行安全十分重要。
神经网络是模仿生物神经元连接结构的一种运算模型,具有并行处理、分布式储存和自学习的能力,在解决非线性和高不确定度问题方面具有优势[1-2]。BP神经网络是一种按照误差逆向传播算法来进行训练的多层前馈神经网络,具有计算量小、简单易行、并行性强的优点,是目前最成熟的神经网络之一,已在对象识别、趋势预测、故障诊断等领域得到广泛应用[3-5]。然而,BP神经网络通常存在学习效率低、收敛速度慢和容易陷入局部极小值的缺点,为了克服这些缺陷,许多学者采用不同的方式对BP神经网络及训练算法进行了改进。
Sun等[6]使用BP神经网络对飞行器控制系统进行了故障诊断,结果显示,诊断的准确率与隐含层的节点数密切相关,且隐含层节点数并非越多越好,若要追求95%以上的高准确性,就需要人为调整隐含层节点数。Zhou等[7]采用灰度关联算法对BP神经网络的结构进行了调整,其主要是在计算过程中对隐含层节点数进行调整,以防止因隐含层节点数量过少而导致学习效果不佳,以及因隐含层节点数量过多而导致的计算资源浪费,结果显示,采用这种改进方法后测试案例的故障诊断准确率可由原来的62.8%提高到77.1%。Lu[8]采用小波模糊算法对BP神经网络结构进行了调整,即在输入层后增加小波分析层用于剔除输入数据的噪音影响,在隐含层前增加模糊层用于对输入信息进行模糊化处理,结果显示,采用这种方法可以显著提高计算残差的收敛速度。张小敏[9]采用L-M算法、自适应动量最速下降法、弹性BP法、拟牛顿算法和共轭梯度法这5种方法对隐含层节点数为8的BP神经网络进行了训练,结果显示L-M算法在案例中的训练效果最优。
综上可以看出,目前有多种手段可对BP神经网络进行改进,但大部分的故障诊断工作受训练样本量、网络构建方法和训练方法的影响,故障诊断的准确率难以保证。为此,本文拟以船舶蒸汽动力系统为对象,首先采用附加动量法对神经网络的计算收敛性进行优化,然后采用自适应学习速率调整法对训练效率进行优化,接着采用灰度关联法对隐含层节点数量进行优化,并提出“小网络集群”的方法对神经网络进行构建,最后使用船舶动力系统仿真平台生成的大量故障数据为神经网络提供学习样本,并针对给水泵转速异常高这一故障现象演示3个故障诊断案例。
1. 优化BP神经网络
1.1 BP神经网络
BP神经网络的训练包含信号的正向传播和误差的反向反馈2个过程。其中正向传播是指在计算时,信号由输入层经并行加权计算后进入隐含层,然后再经过加权处理进入输出层,从而得到输出;而反向反馈过程则是按从输出到输入的方向进行,根据实际误差对权值和阈值进行调整。通过不断重复正向计算与反向反馈,最终使输出结果满足要求。基于BP神经网络的故障诊断模型如图1所示。图中:(
x1,x2,⋯,xj,⋯,xm )为输入量,下标为输入量编号,与输入层节点对应;(y1,y2,⋯,yk,⋯,yl )为输出量,下标为输出量编号,与输出层节点对应;(θ1,θ2,⋯,θi,⋯,θq )为隐含层引入的阈值,下标为隐含节点编号,神经网络中可能有多个隐含层;(a1,a2,⋯,ak,⋯,al )为输出层引入的阈值,下标为输出节点编号,神经网络中仅有1个输出层;ε为误差值。正向传播过程中,隐含层第i个节点的输入ni和输出oi的计算公式如下:
ni=m∑j=1wijxj+θi (1) oi=ϕ(neti)=ϕ(m∑j=1wijxj+θi) (2) 正向传播过程中,输出层第k个节点的输入netk和输出outk的计算公式如下:
netk=q∑i=1wkioi+ak=q∑i=1wkiϕ(m∑j=1wijxj+θi)+ak (3) outk=ψ(netk)=ψ(q∑i=1wkiϕ(m∑j=1wijxj+θi)+ak) (4) 以上式中:wij为第j个输入变量在隐含层第i个节点的权值;
ϕ 为隐含层的激活函数;ψ为输出层的激活函数,为了增强规模化非线性拟合能力,根据实际使用经验,隐含层激活函数选择双极S型的tansig函数,输出层激活函数选择线性的purelin函数。第P个样本的误差函数Ep如式(5)所示,其中Tk为第k个节点的输出期望值。
Ep=12l∑k=1(Tk−outk)2 (5) P个训练样本的总误差E为:
E=12P∑p=1l∑k=1(Tpk−outpk)2 (6) 在反馈过程中,隐含层与输出层的权值修正量和阈值修正量分别可写作
Δwij=−η∂E∂wij, Δθi=−η∂E∂θiΔwki=−η∂E∂wki, Δak=−η∂E∂ak (7) 式中,η为决定调整速率的系数。
1.2 BP算法的改进
采用附加动量法对权值和阈值的调节公式进行修正。每次在对权值或阈值进行修正时,加上一项正比于前次权值或阈值变化量的值,以使神经网络在修正时不仅能够考虑误差在梯度上的作用,还能考虑到误差在曲面上的变化趋势,以帮助越过极小值[10]。隐含层的权值和阈值的调整公式分别如下:
Δwij(N+1)=mc[wij(N)−wij(N−1)]+Δwij(N) (8) Δθi(N+1)=mc[θi(N)−θi(N−1)]+Δθi(N) (9) 输出层的公式与之类似。上式中,N为训练次数;mc为动量因子,其取值规则如下:
mc(N)={0,E(N)>E(N−1)×1.040.95,E(N)<E(N−1)mc(N−1),其他 (10) 采用自适应学习速率的最速下降法来提高BP神经网络的学习效率,缩短训练时间。在每一步反馈之后,检查权值是否真正降低了误差函数E(N),如果E(N)降低,说明调整有效,可适当增大η,反之,则表示产生了过调,应减小η,其取值规则如下:
η(N)={1.05η(N−1),E(N)<E(N−1)0.7η(N−1),E(N)>E(N−1)×1.04η(N−1),其他 (11) 2. 故障诊断实现
2.1 “小网络集群”思路
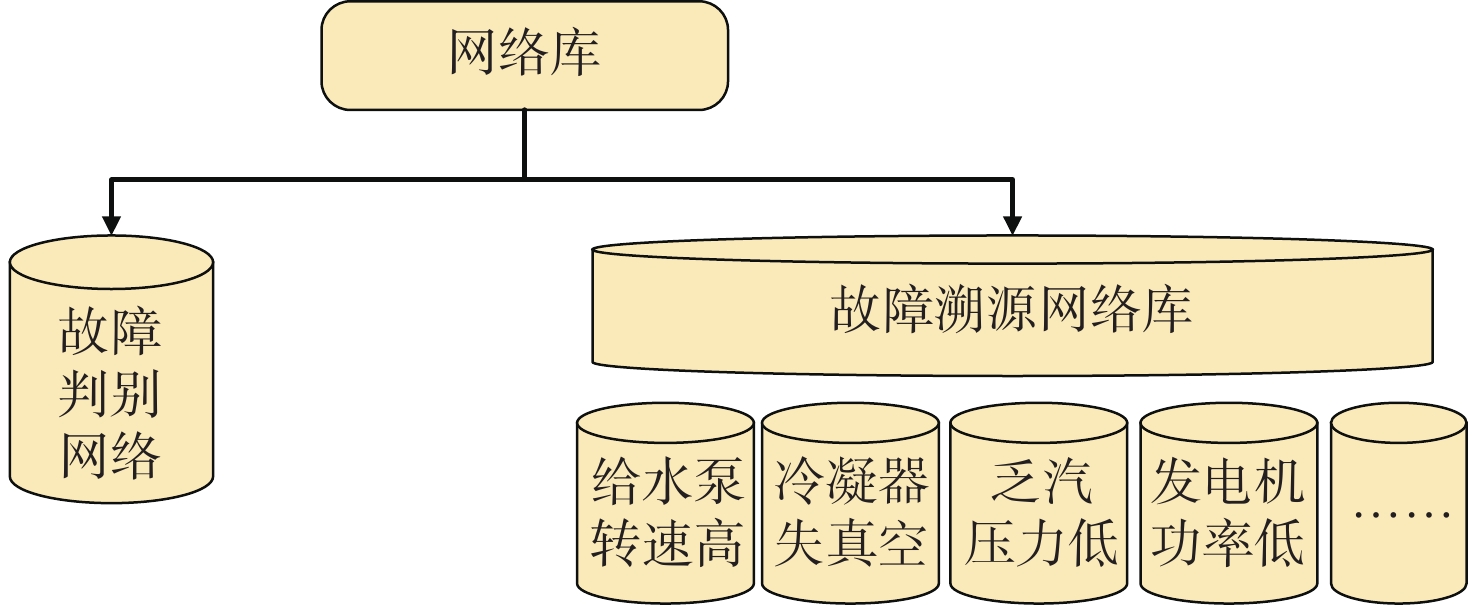
整个船舶动力系统具有海量的监测数据,当某个设备发生故障时,并非所有的参数都会受到影响,为了减少神经网络的复杂程度与训练量,提出了“小网络集群”构建思路,如图2所示。
首先,训练神经网络的故障判别能力。根据故障库中包含的故障,人为识别能够直接反映故障的系统特征参数,例如在给水泵转速高的故障中,给水泵转速是直接反应故障的参数;在乏汽系统压力低的故障中,乏汽压力是直接反应故障的参数等。以这些参数为依据,构建神经网络,训练计算机判别故障的能力。
接着,训练神经网络的故障溯源能力。针对每一个故障现象,分析可能导致故障的原因及相关参数,例如对于给水泵转速高这一故障现象,可能是由于给水泵出口阀开度低、给水泵旁通阀误开、给水泵性能退化所导致,其相关参数分别为给水泵出口阀开度、给水泵旁通阀开度及给水泵性能参数;对于乏汽压力低这一故障现象,可能是由于安全阀回座失效或补汽阀故障所导致,其相关参数为安全阀开度和补汽阀开度。经过故障分析后,针对每一个故障的输入、输出参数量大大降低,网络的复杂程度也大大降低,故可以针对单一故障构建小网络,然后再基于这些小网络建立整个系统的故障诊断神经网络集,实现“小网络集群”,如表1所示。表中,
A =(A1,A2,A3,⋯ ),为故障现象参数集,B =(B1,B2,B3,⋯ ),为故障原因参数集,某一故障现象可能对应多个故障原因参数,通过神经网络的训练,可以使计算机在众多监测数据中判别出故障现象,随之诊断出故障原因。这种方法不仅能有效解决大规模神经网络在训练过程具有的极高时间复杂度和空间复杂度问题,还能方便神经网络局部结构的更新和诊断功能的拓展,可为系统的逐渐完善创造条件。表 1 故障溯源网络库Table 1. Fault source network library网络编号 故障现象 相关参数 故障原因 相关参数
1
给水泵转速高
给水泵转速A1给水泵出口阀故障
给水泵旁通阀打开
给水泵性能退化给水泵出口阀开度B1
给水泵旁通阀开度B2
给水泵性能参数B32 乏汽系统压力低 乏汽压力A2 安全阀回座失效
补汽阀故障安全阀开度B4
补汽阀开度B53 冷凝器失真空 冷凝器压力A3 循环水泵失效
冷凝器换热效能下降循环水泵流量B6
冷凝器换热系数B74 …… …… …… …… 2.2 隐含层优化
隐含层的节点数量对神经网络的诊断准确性存在影响[6],为了提高神经网络结构的自适应性,在“小网络集群”的基础上,采用灰度关联法[7]自动调整小网络的隐含层节点数量。计算机将根据训练结果自动增加隐含层的节点数,直至训练后的精度满足要求。在本文案例中,初始隐含层的节点数量为3个。网络结构调整的基本流程如图3所示。
2.3 故障诊断流程
基于“小网络集群”的故障诊断包含2个方面的内容:故障判别和故障溯源,二者基于不同的网络来实现。由于故障判别主要是基于系统特征参数的偏差进行,所以具有较大的灵活性和批量自动处理能力;而故障溯源则是根据故障判别的结果,先从网格库中筛选合适的小网格并输入参数,然后再进行原因识别。整个故障诊断的流程如图4所示。
3. 故障诊断案例
3.1 问题描述
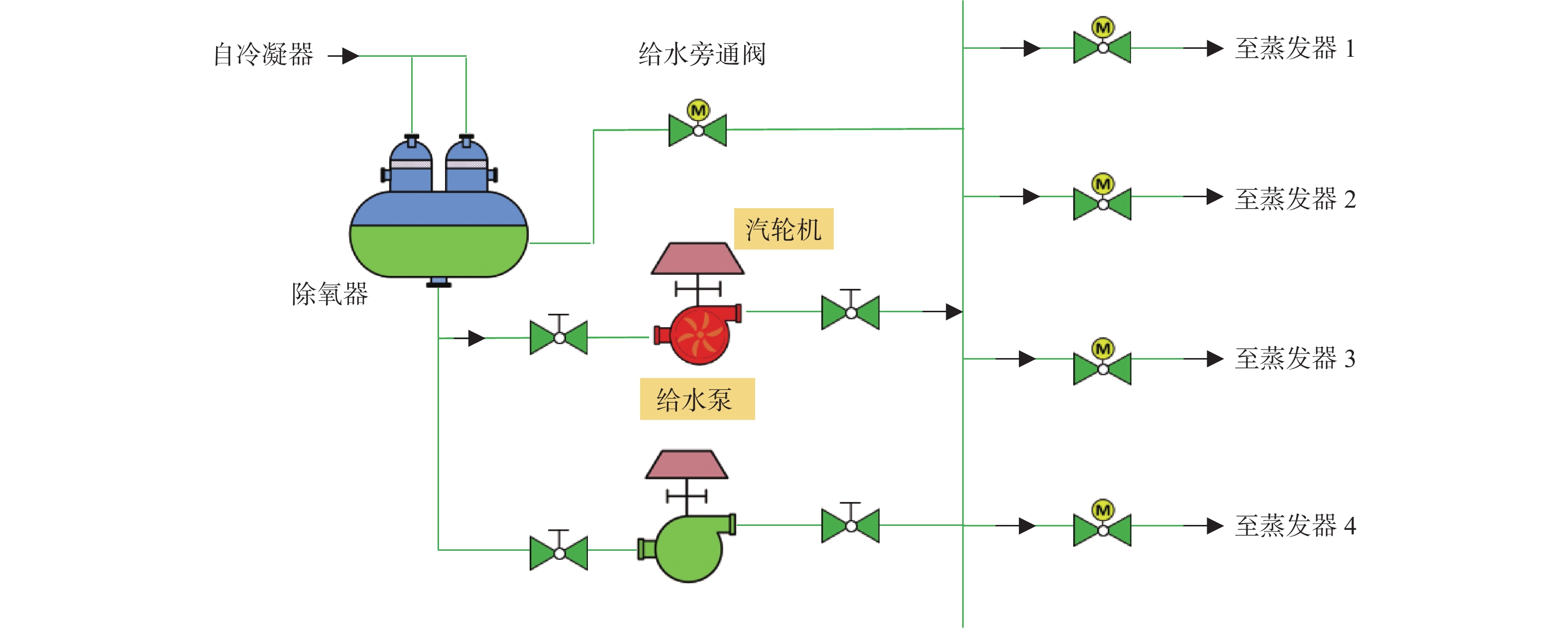
本文将以给水泵转速高这一故障现象为例进行故障诊断演示,给水系统如图5所示。在稳态工况下,给水泵的转速稳定在约6 040 r/min处,波动不超过2%,人为定义当给水泵转速超过6 200 r/min 时发生给水泵转速高的故障。在动力系统仿真平台上进行系统级的仿真,发现导致这一故障的原因可能有3点:一是给水泵出口阀开度低;二是给水泵旁通阀误开;三是给水泵性能退化。以上3种因素均有可能导致给水量减少,在控制系统的调控下,给水泵的转速将自动增加。
3.2 神经网络训练
训练神经网络时,采用1.2节所述自适应学习速率的最速下降法。数据来源于动力系统仿真平台。对于因给水泵出口阀开度低导致的故障,首先确定在正常工况下出口阀的开度值为0.75,然后再使用船舶动力系统仿真平台进行虚拟运行实验,缓慢并逐步降低出口阀的开度值直至0,期间每次调整后,待系统稳定后再记录下给水泵转速与阀门开度数据,并从中挑选出150组训练数据对神经网络进行训练。对于旁通阀故障,在正常稳定工况下旁通阀的开度值为0,在虚拟试验中缓慢并逐步将旁通阀的开度增加至1,期间每次调整后,待系统稳定后再记录下给水泵转速与阀门开度数据,并从中挑选出150组训练数据对神经网络进行训练。对于因给水泵性能退化导致的故障,在正常稳定工况下给水泵的排量性能系数为0.175,在虚拟试验中缓慢并逐步降低性能系数直至0,期间待系统稳定后记录下给水泵转速及排量性能系数,然后从中挑选出150组训练数据对神经网络进行训练。部分实验数据如表2所示。
表 2 部分实验数据Table 2. Part of the experimental data序号 泵转速 /
(r·min−1)给水泵出
口阀开度故障
概率序号 泵转速 /
(r·min−1)旁通流量/
(kg·s−1)故障
概率序号 泵转速 /
(r·min−1)给水泵性能系数 故障
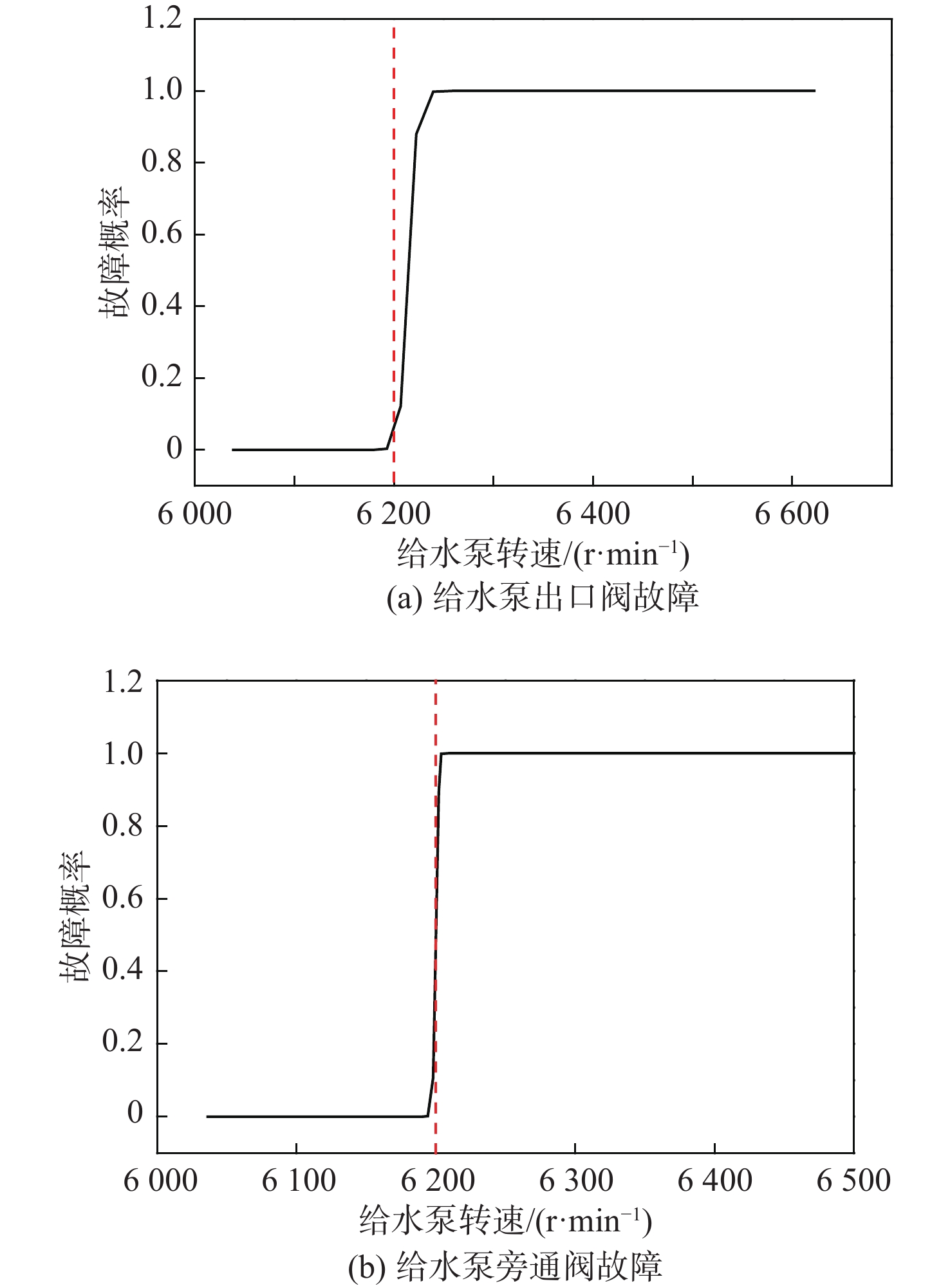
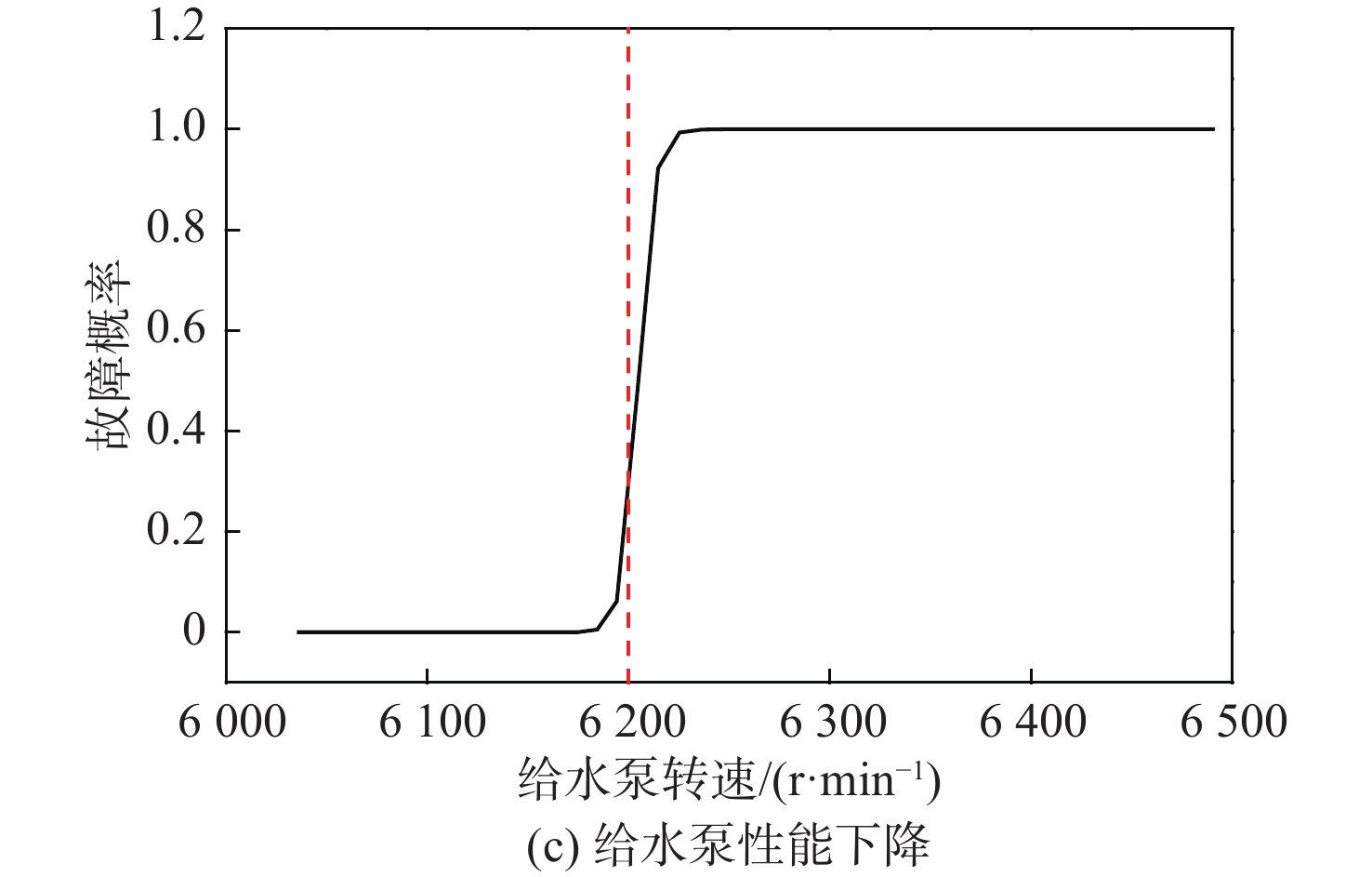
概率1 6 038.531 0.750 0 1 6 036.199 0 0 1 6 036.068 0.175 0 0 2 6 038.919 0.745 0 2 6 036.209 0.5 0 2 6 042.694 0.173 5 0 3 6 039.306 0.740 0 3 6 036.221 1.0 0 3 6 048.575 0.172 0 0 4 6 039.449 0.735 0 4 6 036.232 1.5 0 4 6 054.631 0.170 5 0 5 6 039.592 0.730 0 5 6 045.947 2.0 0 5 6 060.829 0.169 0 0 6 6 039.478 0.725 0 6 6 045.949 2.5 0 6 6 067.010 0.167 5 0 7 6 039.364 0.720 0 7 6 045.951 3.0 0 7 6 073.454 0.166 0 0 8 6 038.978 0.715 0 8 6 050.158 3.5 0 8 6 080.081 0.164 5 0 9 6 038.591 0.710 0 9 6 050.160 4.0 0 9 6 086.597 0.163 0 0 10 6 038.448 0.705 0 10 6 050.160 4.5 0 10 6 093.299 0.161 5 0 11 6 038.304 0.700 0 11 6 050.162 5.0 0 11 6 099.601 0.160 0 0 12 6 038.260 0.695 0 12 6 050.162 5.5 0 12 6 105.930 0.158 5 0 13 6 038.216 0.690 0 13 6 050.164 6.0 0 13 6 112.907 0.157 0 0 14 6 038.291 0.685 0 14 6 054.424 6.5 0 14 6 120.920 0.155 5 0 15 6 038.366 0.680 0 15 6 054.427 7.0 0 15 6 129.145 0.154 0 0 16 6 039.158 0.675 0 16 6 054.430 7.5 0 16 6 137.635 0.152 5 0 17 6 039.949 0.670 0 17 6 058.646 8.0 0 17 6 146.589 0.151 0 0 18 6 040.806 0.665 0 18 6 058.649 8.5 0 18 6 146.593 0.149 5 0 19 6 041.663 0.660 0 19 6 058.652 9.0 0 19 6 156.146 0.148 0 0 20 6 042.403 0.655 0 20 6 062.650 9.5 0 20 6 065.819 0.146 5 0 … … … … … … … … … … … … 训练完成后,针对每一种故障模式,各挑选50组测试数据检验神经网络的训练效果。测试结果如图6所示,其计算数值表示在当前故障模式下,由当前原因导致故障产生的概率。由图可以看出,当给水泵转速低于6 200 r/min时,各故障模式下的诊断结果均为0;当给水泵转速超过6 200 r/min时,各故障模式下的诊断结果均为1;当给水泵转速约为6 200 r/min时,各故障模式下的诊断结果为0~1之间的某一值,对其四舍五入取值后,认为当该值大于等于0.5时表示发生了该故障,小于0.5则表示未发生故障,可以认为针对测试数据的故障诊断准确率高达99%以上。
3.3 故障诊断结果
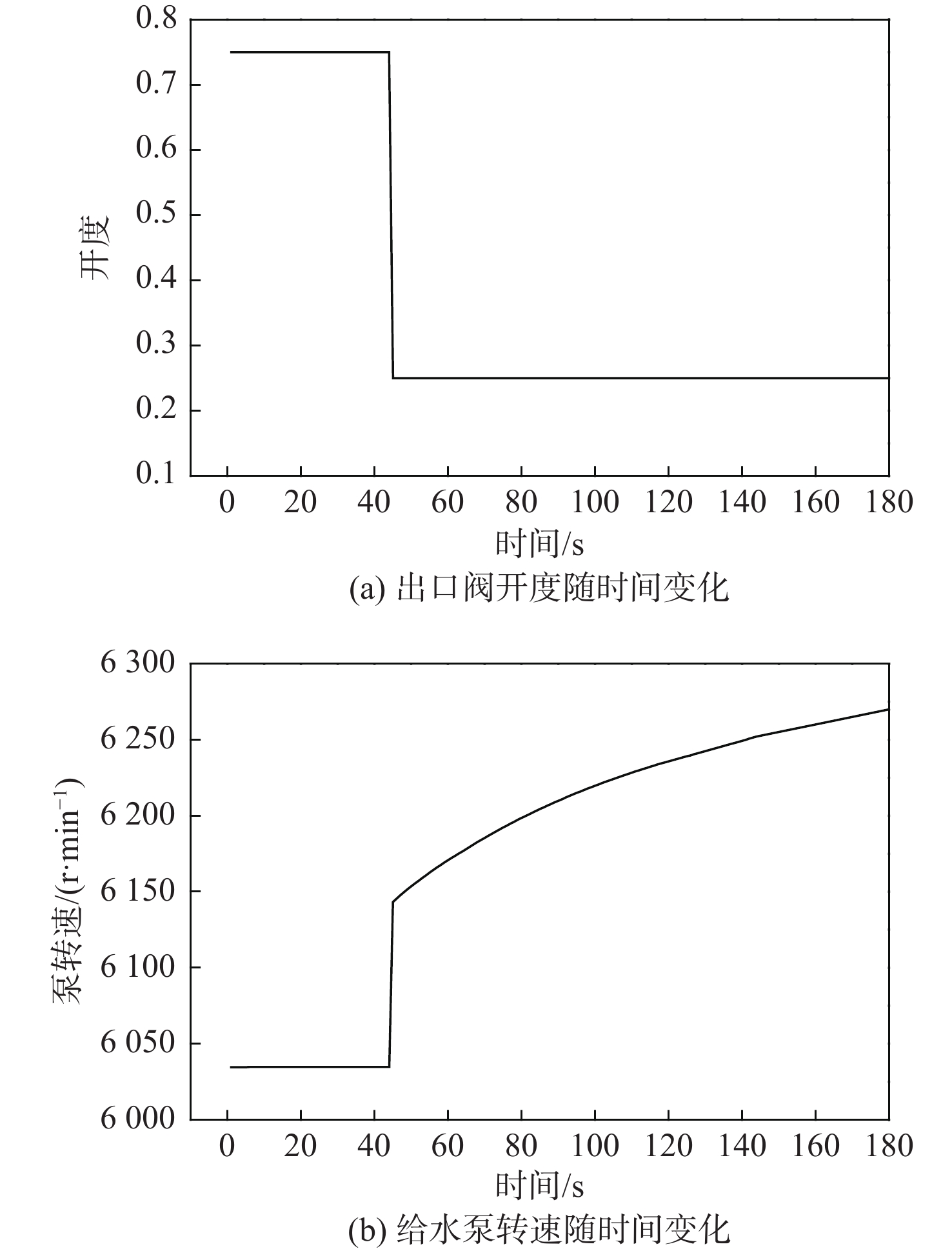
训练完成后,针对每一种故障模式在系统仿真软件中人为设置3种故障,并使用故障诊断工具实时进行故障监测。在仿真系统正常运行工况下,将给水阀出口开度由0.75修改为0.25,给水泵的转速不断升高,如图7所示。当给水泵转速超过6 200 r/min时,故障诊断工具会发出报警,如图8所示,其识别出的故障类型为“1#给水泵转速高”,故障原因为“给水泵出口阀故障”,故障概率为100%。
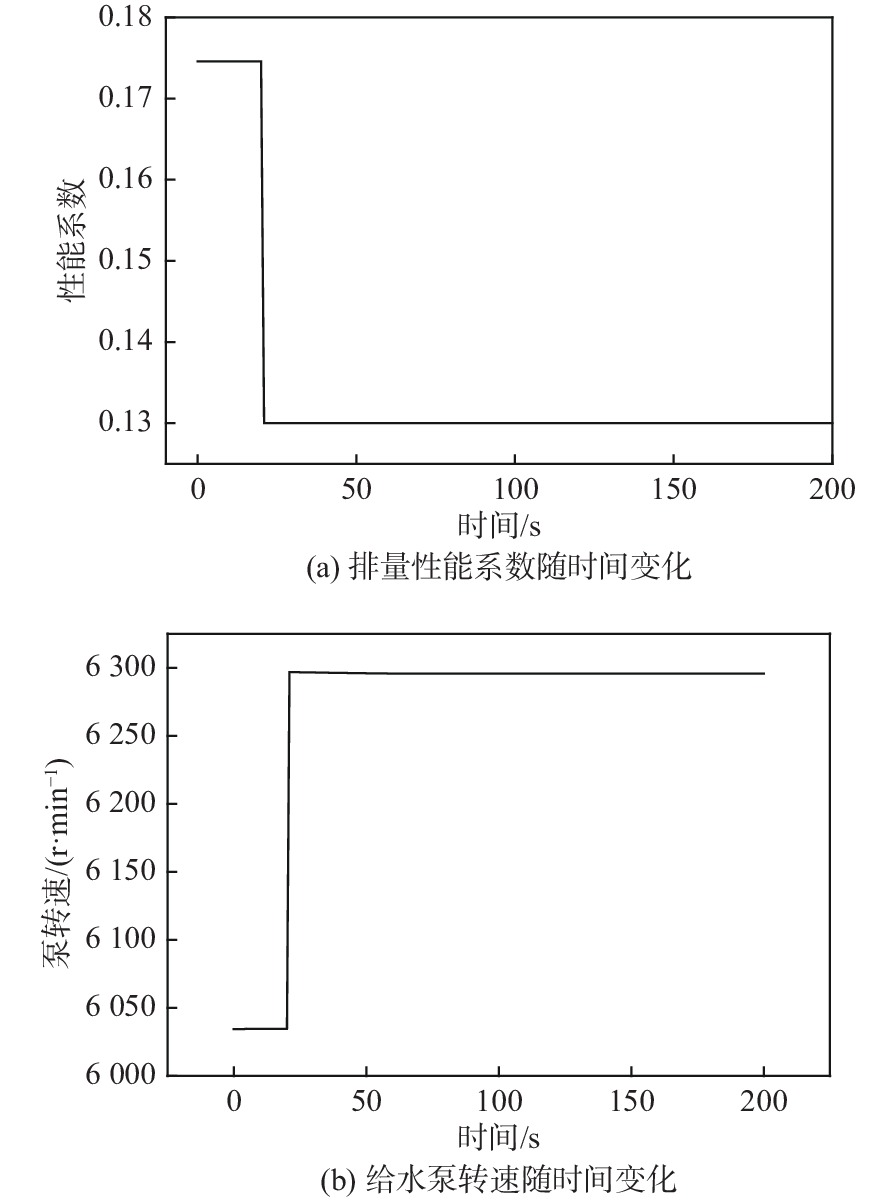
在仿真系统正常运行工况下,将给水泵排量性能系数由0.175修改为0.13,给水泵转速不断升高,如图9所示。当给水泵转速超过6 200 r/min时,故障诊断工具发出报警,如图10所示,其识别出的故障类型为“1#给水泵转速高”,故障原因为“给水泵运行失效”,故障概率为100%。
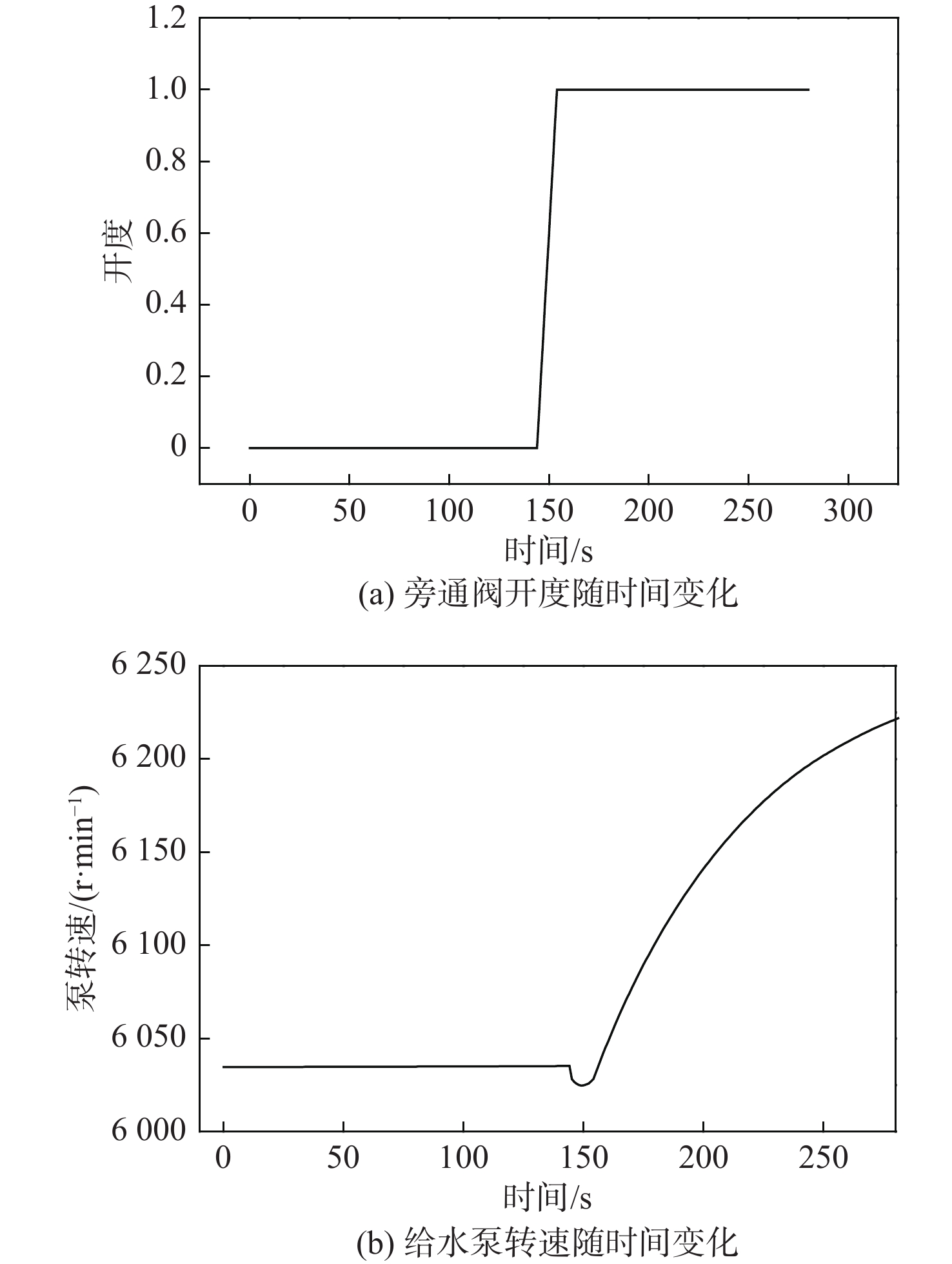
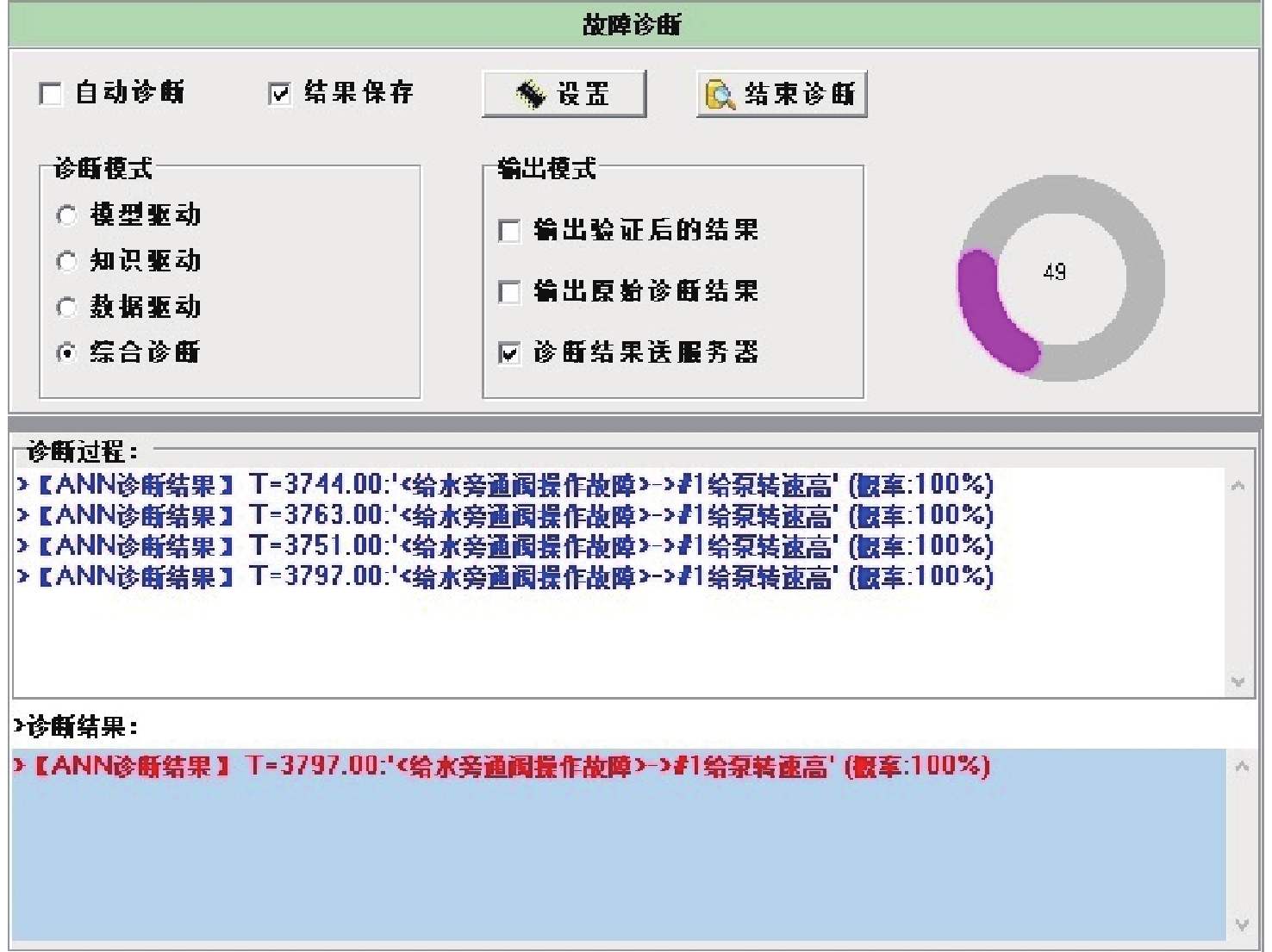
在仿真系统正常运行工况下,将给水旁通阀打开,旁通阀开度由0变为1,给水泵转速不断升高,如图11所示。当给水泵转速超过6 200 r/min时,故障诊断工具发出报警,如图12所示,其识别出的故障类型为“1#给水泵转速高”,故障原因为“给水旁通阀故障”,故障概率为100%。
4. 结 语
本文以BP神经网络为基础,提出了一种针对船舶动力系统的故障诊断方法,即采用附加动量法对神经网络的计算收敛性进行优化,采用自适应学习速率调整法对训练效率进行优化,采用灰度关联法对隐含层节点数量进行优化,并提出了一种“小网络集群”的方法来构建神经网络,以在机器学习阶段将故障现象相关数据与故障原因相关数据区分开来,从而在网络构建阶段将故障判别网络与故障溯源网络库区分开来,最后,采用动力系统仿真平台生成的大量仿真数据为神经网络提供训练和测试样本,结果显示经过训练后样本数据的诊断准确率可达99%以上。
-
表 1 故障溯源网络库
Table 1 Fault source network library
网络编号 故障现象 相关参数 故障原因 相关参数
1
给水泵转速高
给水泵转速A1给水泵出口阀故障
给水泵旁通阀打开
给水泵性能退化给水泵出口阀开度B1
给水泵旁通阀开度B2
给水泵性能参数B32 乏汽系统压力低 乏汽压力A2 安全阀回座失效
补汽阀故障安全阀开度B4
补汽阀开度B53 冷凝器失真空 冷凝器压力A3 循环水泵失效
冷凝器换热效能下降循环水泵流量B6
冷凝器换热系数B74 …… …… …… …… 表 2 部分实验数据
Table 2 Part of the experimental data
序号 泵转速 /
(r·min−1)给水泵出
口阀开度故障
概率序号 泵转速 /
(r·min−1)旁通流量/
(kg·s−1)故障
概率序号 泵转速 /
(r·min−1)给水泵性能系数 故障
概率1 6 038.531 0.750 0 1 6 036.199 0 0 1 6 036.068 0.175 0 0 2 6 038.919 0.745 0 2 6 036.209 0.5 0 2 6 042.694 0.173 5 0 3 6 039.306 0.740 0 3 6 036.221 1.0 0 3 6 048.575 0.172 0 0 4 6 039.449 0.735 0 4 6 036.232 1.5 0 4 6 054.631 0.170 5 0 5 6 039.592 0.730 0 5 6 045.947 2.0 0 5 6 060.829 0.169 0 0 6 6 039.478 0.725 0 6 6 045.949 2.5 0 6 6 067.010 0.167 5 0 7 6 039.364 0.720 0 7 6 045.951 3.0 0 7 6 073.454 0.166 0 0 8 6 038.978 0.715 0 8 6 050.158 3.5 0 8 6 080.081 0.164 5 0 9 6 038.591 0.710 0 9 6 050.160 4.0 0 9 6 086.597 0.163 0 0 10 6 038.448 0.705 0 10 6 050.160 4.5 0 10 6 093.299 0.161 5 0 11 6 038.304 0.700 0 11 6 050.162 5.0 0 11 6 099.601 0.160 0 0 12 6 038.260 0.695 0 12 6 050.162 5.5 0 12 6 105.930 0.158 5 0 13 6 038.216 0.690 0 13 6 050.164 6.0 0 13 6 112.907 0.157 0 0 14 6 038.291 0.685 0 14 6 054.424 6.5 0 14 6 120.920 0.155 5 0 15 6 038.366 0.680 0 15 6 054.427 7.0 0 15 6 129.145 0.154 0 0 16 6 039.158 0.675 0 16 6 054.430 7.5 0 16 6 137.635 0.152 5 0 17 6 039.949 0.670 0 17 6 058.646 8.0 0 17 6 146.589 0.151 0 0 18 6 040.806 0.665 0 18 6 058.649 8.5 0 18 6 146.593 0.149 5 0 19 6 041.663 0.660 0 19 6 058.652 9.0 0 19 6 156.146 0.148 0 0 20 6 042.403 0.655 0 20 6 062.650 9.5 0 20 6 065.819 0.146 5 0 … … … … … … … … … … … … -
[1] 韩小溪, 胡光振, 杨元. 基于BP神经网络的维修性设计参数灵敏度分析[J]. 中国舰船研究, 2008, 3(6): 66–69. doi: 10.3969/j.issn.1673-3185.2008.06.016 HAN X X, HU G Z, YANG Y. Sensitivity analysis of maintainability design parameters based on BP neural network[J]. Chinese Journal of Ship Research, 2008, 3(6): 66–69 (in Chinese). doi: 10.3969/j.issn.1673-3185.2008.06.016
[2] 郭江华, 侯馨光, 陈国钧, 等. 船舶柴油机故障诊断技术研究[J]. 中国航海, 2005(4): 75–78. doi: 10.3969/j.issn.1000-4653.2005.04.020 GUO J H, HOU X G, CHEN G J, et al. Research on fault diagnosis technology of marine diesel engine[J]. Navigation of China, 2005(4): 75–78 (in Chinese). doi: 10.3969/j.issn.1000-4653.2005.04.020
[3] 钱华明, 王雯升. 遗传神经网络在导航传感器故障诊断中的应用[J]. 中国航海, 2009, 32(1): 6–9. doi: 10.3969/j.issn.1000-4653.2009.01.002 QIAN H M, WANG W S. Application of improved genetic BP network in inertia navigation fault diagnosis[J]. Navigation of China, 2009, 32(1): 6–9 (in Chinese). doi: 10.3969/j.issn.1000-4653.2009.01.002
[4] WU G Q. Fault detection method for ship equipment based on BP neural network [C]//2018 International Conference on Robots & Intelligent System. Changsha: IEEE, 2018: 556-559.
[5] WANG X M, WANG J, PRIVAULT M. Artificial intelligent fault diagnosis system of complex electronic equipment[J]. Journal of Intelligent & Fuzzy Systems, 2018, 35(4): 4141–4151.
[6] SUN D S, QIAO N, LIU B, et al. Fault diagnosis of flight control system based on BP neural network observer [C]//Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference. Nanjing, China, 2016: 2570-2575.
[7] ZHOU W P, SUN D L, WANG J L. Fault diagnosis of ship power supply system based on grey correlation improved BP neural network [C]//2015 Chinese Automation Congress. Wuhan, China: IEEE, 2015: 1203-1208.
[8] LU B Y. Application of the wavelet fuzzy BP network in the automotive fault diagnosis[J]. Applied Mechanics and Materials, 2014, 668-669: 458–461. doi: 10.4028/www.scientific.net/AMM.668-669.458
[9] 张小敏. 基于神经网络的飞控传感器故障诊断[D]. 南京: 南京航空航天大学, 2012. ZHANG X M. Sensor fault diagnosis for flight control system based on neural network [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012 (in Chinese).
[10] 罗黎. 神经网络在船舶电力推进系统故障诊断中的应用[J]. 舰船科学技术, 2016, 38(6A): 97–99. LUO L. Application of neural network in fault diagnosis of ship electric propulsion system[J]. Ship Science and Technology, 2016, 38(6A): 97–99 (in Chinese).



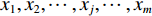
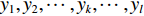
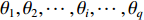
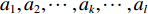

 下载:
下载: