避雷针防护概率数值评估方法

王帮勇; 陆佳骏; 祁德; 张旭东; 曹斌; 郭俊; 谢彦召

doi:10.19693/j.issn.1673-3185.02483

避雷针防护概率数值评估方法

王帮勇^1,,
陆佳骏²,
祁德²,
张旭东¹,
曹斌²,
郭俊^1, ,,
谢彦召^1,

1.
西安交通大学电气工程学院，陕西西安 710049
2.
中国船舶及海洋工程设计研究院，上海 200011

基金项目: 国家自然科学基金资助项目（51807158）；强脉冲辐射环境模拟与效应国家重点实验室资助项目（SKLIPR1909）

详细信息

作者简介:
王帮勇，男，1995年生，硕士生。研究方向：雷电模拟及防雷技术。E-mail：a523941858@stu.xjtu.edu.cn

郭俊，男，1986年生，博士，副教授。研究方向：多导体传输线瞬态分析，瞬态电磁场测量等。E-mail：junguo@mail.xjtu.edu.cn

谢彦召，男，1973年生，博士，教授，博士生导师。研究方向：电磁兼容与电磁安全。E-mail：yanzhao.xie@gmail.com

通讯作者:
郭俊

中图分类号: U665.2
计量
- 文章访问数: 540
- HTML全文浏览量: 163
- PDF下载量: 65
出版历程
- 收稿日期: 2021-08-10
- 修回日期: 2021-09-03
- 网络出版日期: 2021-09-09
- 刊出日期: 2023-04-27

Numerical evaluation method of lightning rod protection probability

1.
School of Electrical Engineering, Xi'an Jiaotong University, Xi'an 710049, China
2.
Marine Design and Research Institute of China, Shanghai 200011, China

避雷针防护概率数值评估方法王帮勇，采用知识共享署名4.0国际许可协议进行许可。

摘要

摘要:
目的针对传统避雷针防护效能评估方法难以对其防护概率进行高效评估的现状，基于电气几何模型和引雷空间理论发展一种避雷针防护概率数值评估高效算法，实现避雷针对空间任意点防护概率的高效计算。
方法首先，根据上下行先导的拦截过程确定避雷针与保护物的引雷空间边界；然后，再由雷击距画出受雷曲面与暴露弧，通过分析受雷曲面和暴露弧的不同特征，量化评估避雷针的引雷风险与接闪效能；最后，综合避雷针引雷与防雷两方面特性建立防护概率的数值评估模型。为检验该方法的准确性，分析避雷针防护概率变化的一般规律，并将结果与已有的分析方法进行对比。
结果结果表明，该方法的评估结果与经典雷电先导发展模型理论的雷击模拟结果相符。
结论该方法量化程度高，可以实现避雷针对空间任一点防护概率的高效计算，有助于防雷设计工作。
- 避雷针 /
- 引雷空间 /
- 防护概率 /
- 数值评估
Abstract:
Objectives Aiming at the current situation in which it is difficult to efficiently evaluate protection probability through traditional lightning rod evaluation methods, an efficient numerical evaluation algorithm is developed on the basis of an electrogeometric model (EGM) and attractive volume to realize the efficient calculation of lightning protection probability at any point in space.
Methods This method first determines the attractive volume boundary of the lightning rod and protection object according to the interception process of the upward and downward leaders. The collection surface and exposure arc of the lightning stroke distance are then calculated, enabling the attractive risk and interception effect of the lightning rod to be quantified. Finally, the attraction and interception characteristics of the lightning rod are integrated to establish a numerical evaluation model of protection probability. To verify the accuracy of this method, the general rule of lightning rod protection probability is analyzed and the results compared with the existing analysis method.
Result The evaluation results of this method show good agreement with those of classical leader progression model (LPM) theory.
Conclusions The method proposed herein has a high degree of quantification and can realize the efficient calculation of lightning protection probability at any point in space, which can provide useful references for lightning protection design work.
- lightning rod /
- attractive volume /
- protection probability /
- numerical evaluation

HTML全文

0. 引　言

避雷针作为国内外公认的直击雷防护装置，其接闪效能的评估是防雷设计的重要依据。尽管国内外的标准中已经给出了传统避雷针保护范围的设计计算方法，但由于其保护范围只是一定允许雷击概率下的统计区域，无法对空间任一点的防护概率进行数值分析。随着经济社会的不断发展，被保护物的高度不断增加，按照传统雷电防护设计方法配置避雷针后，保护物被雷击的现象仍频繁发生，亟需发展新的反映避雷针防护效能的数值评估方法。

我国对避雷针系统雷电防护效能的评估主要采用折线法^{[1- 2]}，根据经验及小电流试验模型绘制一定允许雷击概率下的保护范围，未考虑雷电强度及其发展的随机过程对避雷针接闪性能的影响，往往不能达到预期的防护效果；国际上常用的基于电气几何模型（electrogeometric model，EGM）的滚球法（RSM）^[3-6]将雷击距与雷电流大小联系起来，用几何作图的方式来绘制避雷针的保护范围，考虑了保护物结构及高度的影响，具有一定的物理意义，但该方法忽略了上行先导的拦截过程，导致其保护范围的标准过于严格。传统的避雷针防护效能评估方法均是通过绘制保护范围，认为其范围内的物体可受到避雷针的防护，但是无法对其内部任意点的防护概率进行量化计算，难以发现保护物的雷电薄弱环节。

实际上，目前国内外并没有系统及定量的方法来描述避雷针接闪的有效性。随着对雷电观测和长间隙放电试验的研究，Dellera等^[7-10]提出并发展了先导发展模型（leader progression model，LPM），对上下行先导起始、发展和二者的连接过程建立了合理的数学模型，借助计算机编程，可实现雷电放电过程的仿真模拟。根据多次仿真结果确定避雷针的防护概率，进而发现防雷系统的薄弱环节^[11-13]。但采用LPM对避雷针系统进行防护概率的量化计算通常要进行成百上千次雷电放电过程的模拟，受限于计算机的算力资源，该方法费时费力，无法实现避雷针防护概率的高效计算。

鉴于此，本文将基于电气几何模型，借助引雷空间理论，提出一种避雷针防护概率数值评估方法，综合考虑雷电下行先导入射方向及其强度的随机性、地区雷电活动强度以及保护物的位置和高度等信息，建立避雷针防护概率理论数值评估方法，实现对避雷针防护概率的快速计算，进而高效指导防雷设计工作。

1. 电气几何模型与引雷空间

1.1 电气几何模型

1945年，Golde^[4]结合前人的研究成果将雷电击距与雷电流幅值联系起来，奠定了电气几何模型的基础。电气几何模型把表征雷电物理过程的电气参量用几何参数表示，以击距的形式来描述地面各导体的引雷能力与受雷范围，通过几何画图的方式模拟雷电的随机性，进而来表示不同雷电强度下的避雷针屏蔽效果。

Golde发展的关系式可表示为

${R_{\text{s}}} = a{I^b}$

(1)

式中： ${R_{\text{s}}}$ 为雷电击距； $I$ 为雷电流幅值；a，b为常数，不同学者的取值各不相同。

由于自然雷电强度具有随机性，雷电流幅值的大小满足一定的概率分布^[5]：

$f\left( I \right) = \frac{\eta }{{{I_0}^\eta }} \cdot \frac{{{I^{\left( {\eta - 1} \right)}}}}{{{{\left[ {1 + {{\left( {I/{I_0}} \right)}^\eta }} \right]}^2}}}$

(2)

式中： $\eta$ 和I₀为待求参数，其值能反映各地区雷电活动强度，使雷电屏蔽分析模型具有更强的区域适应性。联立式(1)和式(2)，可得到对应击距 ${R_{\text{s}}}$ 的概率密度函数

$f\left( {{R_{\text{s}}}} \right) = \frac{\eta }{{{I_0}^\eta }} \cdot \frac{{{{\left( {{a^{ - 1}}{R_{\text{s}}}} \right)}^{\frac{{^{\left( {\eta - 1} \right)}}}{b}}}}}{{{{\left[ {1 + {{\left( {{{\left( {{a^{ - 1}}{R_{\text{s}}}} \right)}^{\frac{1}{b}}}/{I_0}} \right)}^\eta }} \right]}^2}}}$

(3)

1.2 引雷空间

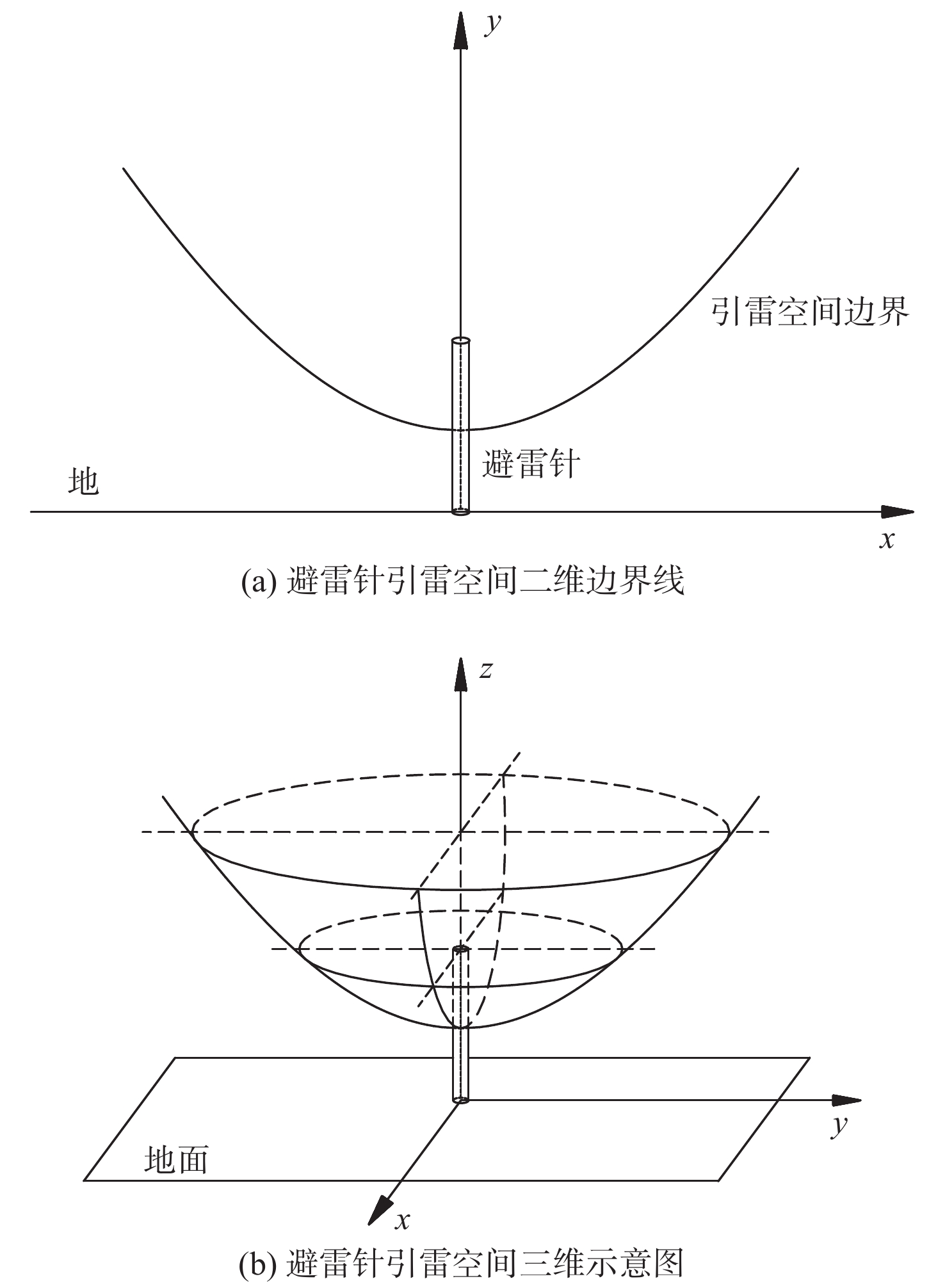
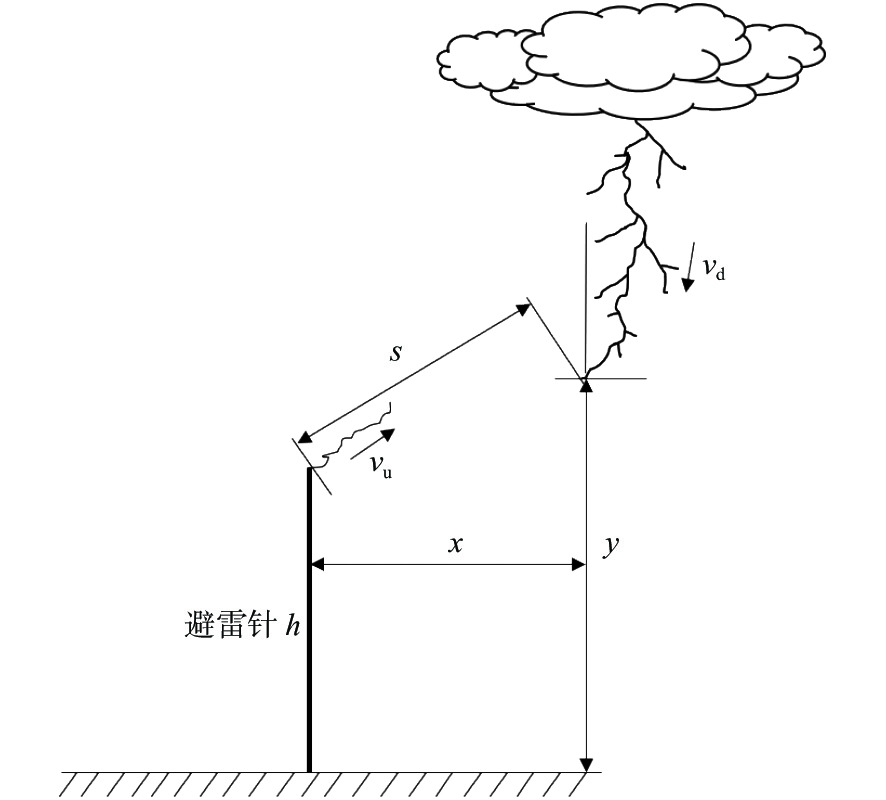
引雷空间的概念最早由南非学者Eriksson提出并应用于避雷针系统防雷效能分析中^[14]。图1为避雷针的引雷示意图。图中，x为下行先导到避雷针的水平距离；h为避雷针高度。雷电下行先导从雷云向地面随机发展，当下行先导头部行进到某一高度时，避雷针顶端将产生上行先导，导致下行先导发展的随机性减弱，转而向上行先导所在方向定向发展，此时下行先导头部所在位置被称为定向点，为确保该定向点可被避雷针产生的上行先导拦截，可近似认为避雷针上行先导到达定向点的时间要快于下行先导到达地面的时间，即

图 1 避雷针的引雷示意图

Figure 1. Schematic diagram of conducting the lightning to the ground via lightning rod

下载: 全尺寸图片幻灯片

$\frac{s}{{{v_{\text{u}}}}} < \frac{y}{{{v_{\text{d}}}}}$

(4)

式中：s为避雷针顶点到下行先导头部的距离；y为下行先导头部到地面的竖直距离； ${v_{\text{u}}}$ 和 ${v_{\text{d}}}$ 分别为上行先导和下行先导的发展速度。

结合图中几何关系，式(4)取等号，即可得到避雷针引雷空间边界线的表达式：

$x = \sqrt {{{\left( {\frac{y}{{{\lambda _{\rm{v}}}}}} \right)}^2} - {{\left( {y - h} \right)}^2}}$

(5)

式中， ${\lambda _{\rm{v}}} = {v_{\text{d}}}/{v_{\text{u}}}$ 。根据国内外雷电观测及长间隙放电试验研究结果^{[7, 9, 15]}，先导在起始阶段的发展速度比为4∶1，即 ${\lambda _{\rm{v}}} = 4$ ，此后，上行先导发展速度随着下行先导的发展逐渐增加，在上下行先导发展的最后阶段，其速度比约为1∶1，即 ${\lambda _{\rm{v}}} = 1$ 。故式(5)可进一步简化为

$x = \sqrt {2yh - {h^2}}$

(6)

式(6)为xy平面的一条二次曲线，如图2(a)所示。将该曲线沿着避雷针轴线旋转，可得到避雷针的引雷空间三维边界，如图2(b)所示。定向点在该空间内的雷电下行先导均有可能向避雷针发展进而被其拦截，反之，认为引雷空间外的下行先导定向点将不会被避雷针拦截。

图 2 避雷针引雷空间边界

Figure 2. The atrractive volume boundary of lightning rod

下载: 全尺寸图片幻灯片

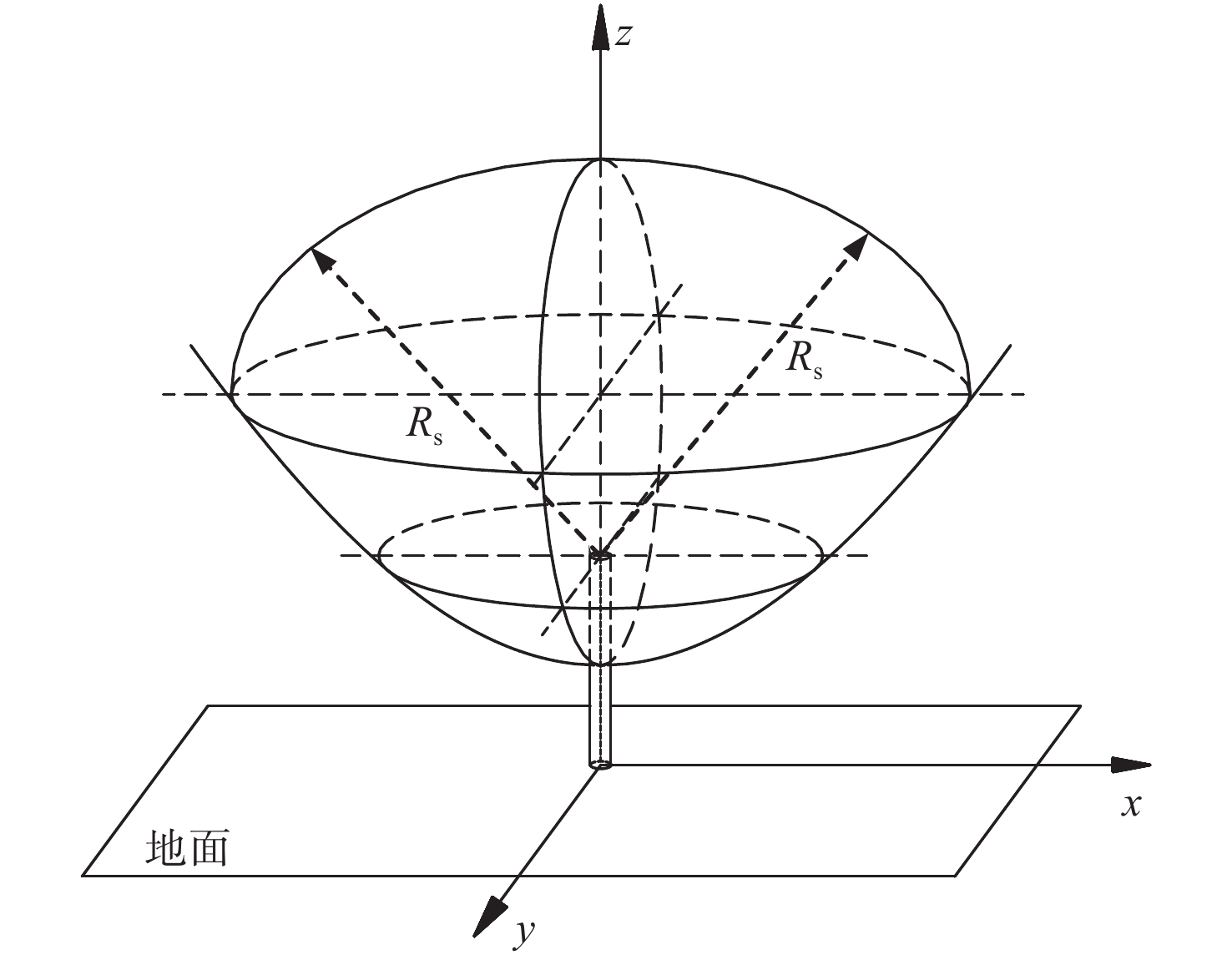
以避雷针顶点为球心，雷击距 ${R_{\text{s}}}$ 为半径作球面，该球面与引雷空间边界所围成的球冠面即为避雷针的受雷曲面，如图3所示。当雷击距为 ${R_{\text{s}}}$ 的下行先导定向点到达该曲面时，认为其一定会被避雷针产生的上行先导拦截。 ${R_{\text{s}}}$ 作为表征雷电能量的参数，其不同的取值代表着每次雷击时雷电强度的随机性，即避雷针的受雷曲面也存在随机性，反映避雷针对不同强度雷电的拦截能力具有差异性。

图 3 避雷针在雷击距为R_s时的受雷曲面

Figure 3. Collection surface of lightning rod at the stroke distance of R_s

下载: 全尺寸图片幻灯片

引雷空间理论是对传统滚球法理论的延伸，考虑了地闪过程中上行先导的拦截作用，结合雷电击距的随机性，使避雷针防护概率的分析过程更具物理意义。

2. 避雷针防护概率数值评估方法

2.1 避雷针带来的引雷风险

因避雷针自身的高引雷特性会导致其所在区域的落雷密度增加，一定程度上增加了该区域雷击事件发生的概率，降低了避雷针的防护效能。通常云地放电才能构成对电力系统设备或建筑的直接危害，避雷针引雷风险的评估需要了解有多少雷电是向地面发展的，GB 50057—2010《建筑物防雷设计规范》规定了建筑物的年雷击次数^[16]：

$N = k \cdot {N_{\text{g}}} \cdot {A_{\text{e}}}$

(7)

式中：k为地形影响因子；N_g为建筑物所处地区雷击大地的年平均密度；A_e为与建筑物截收相同雷击次数的等效暴露面积。N_g的取值首先应根据当地雷电活动情况确定，一般为

${N_{\text{g}}} = \gamma \cdot {T_{\text{d}}}$

(8)

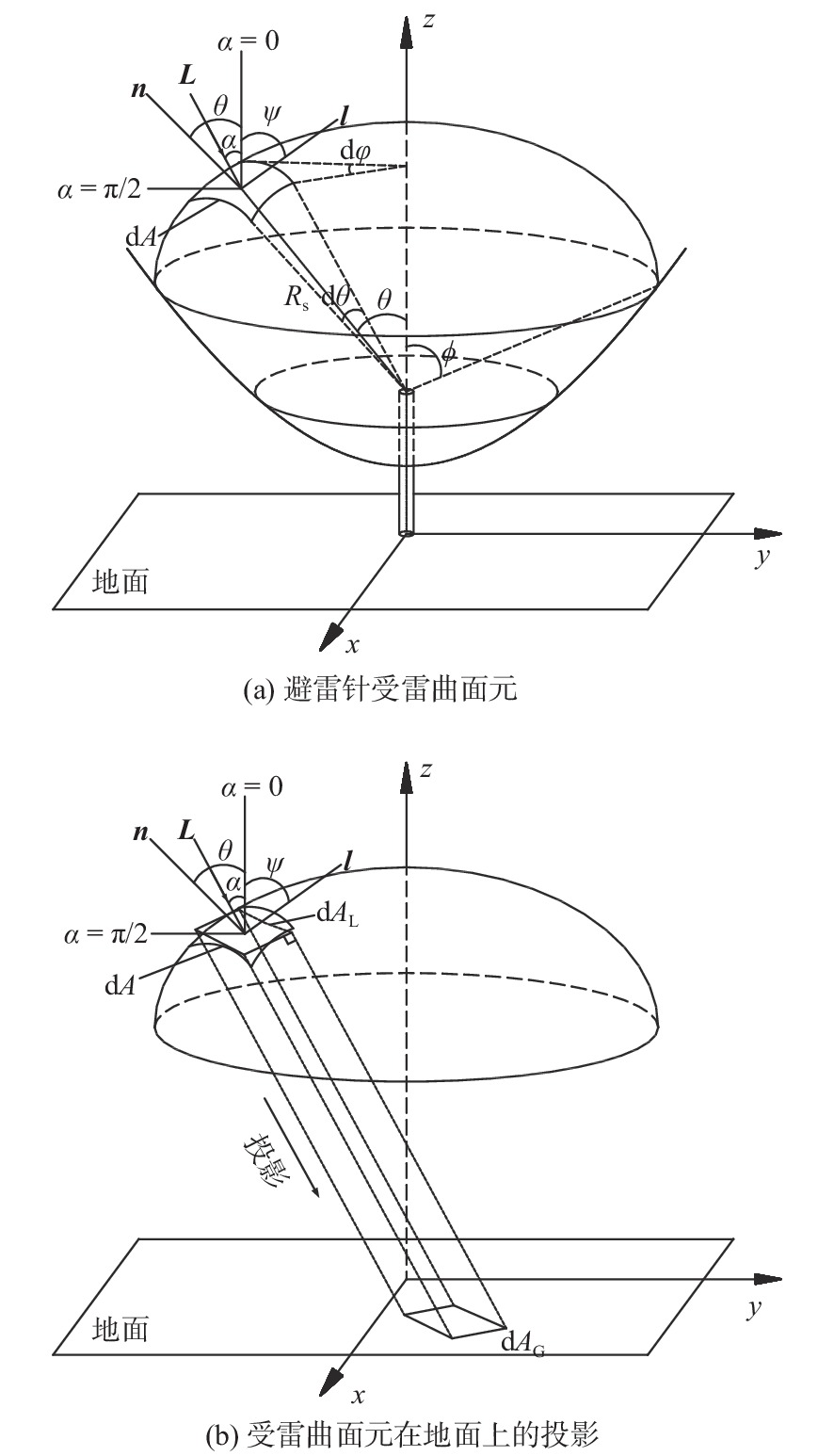
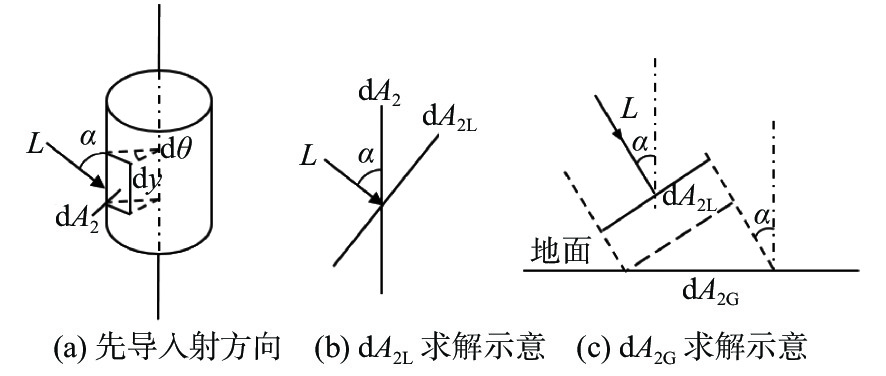
式中： $\gamma$ 为地面落雷密度； ${T_{\text{d}}}$ 为年平均雷暴日。为了得到避雷针的年预计雷击次数，需要获取与避雷针截收相同雷击次数的等效暴露面积A_e，而GB 50057—2010中规定的等效暴露面积算法仅针对建筑物，以扩大建筑物宽度求得其等效暴露面积，并不适用于避雷针这类水平尺寸很小而竖直尺寸很大的杆体。如图3所示，避雷针的等效暴露面积可由其受雷曲面求得。对于不同强度的雷电下行先导，避雷针的受雷曲面是不一样的，即避雷针的等效暴露面积不应只是其几何尺寸的关系式，还应考虑下行先导的强度和入射方向。由于等效暴露面积需要求取受雷曲面在地面上的投影面积，考虑最严重的情况，本文认为避雷针的等效暴露面积等于受雷曲面在沿着下行先导入射方向的地面上的投影面积^[17]，进而预测避雷针的年引雷次数。

图4为避雷针等效暴露面积计算方法示意图。在受雷曲面上任取一个微分曲面元，其中l，n和L分别为该微分曲面元的切线、外法线和下行先导入射方向，其微分面积 ${\text{d}}A$ 为

图 4 避雷针等效暴露面积计算方法

Figure 4. Calculation method of equivalent exposure area of lightning rod

下载: 全尺寸图片幻灯片

$\begin{split} &\;\\& {\text{d}}A = {R_{\text{s}}}^2\sin \theta {\text{d}}\theta {\text{d}}\varphi \end{split}$

(9)

式中： $\theta$ 为微分面积 ${\text{d}}A$ 与竖直方向的夹角； $\varphi$ 为该微分面积在xy平面投影与x轴正方向的夹角。微分面积 ${\text{d}}A$ 在垂直于下行先导L方向上的投影 ${\text{d}}{A_L}$ 为

${\text{d}}{A_L} = {R_{\text{s}}}^2\sin \theta \cos \left( {\alpha - \theta } \right){\text{d}}\theta {\text{d}}\varphi$

(10)

式中： $\alpha$ 为下行先导入射方向与竖直方向的夹角。 $\alpha$ 的取值具有随机性，根据实测的数据统计结果， $\alpha$ 的概率密度函数 $g\left( \alpha \right)$ 可表示为^[18]

$g\left( \alpha \right) = \frac{2}{{\text{π }}}{\cos ^2}\alpha {\text{ }}\psi \leqslant \alpha \leqslant \frac{{\text{π}}}{2}$

(11)

式中： $\psi$ 为微分面积 ${\text{d}}A$ 的切线l在竖直方向上的夹角。 ${\text{d}}{A_L}$ 沿着下行先导方向L入射到地面上的微分面积为

${\text{d}}{A_{\text{G}}} = \frac{{{R_{\text{s}}}^2\sin \theta \cos \left( {\alpha - \theta } \right){\text{d}}\theta {\text{d}}\varphi }}{{\cos \alpha }}$

(12)

因此，避雷针在某一击距 ${R_{\text{s}}}$ 下的等效暴露面积为

${A_{{\text{eq1}}}} = \int_\psi ^{\frac{{\text{π}} }{2}} {\left( {\int_0^\phi {\int_0^{2{\text{π}} } {\frac{{{R_{\text{s}}}^2\sin \theta \cos \left( {\alpha - \theta } \right)}}{{\cos \alpha }}{\text{d}}\theta {\text{d}}\varphi } } } \right)} \cdot g\left( \alpha \right){\text{d}}\alpha$

(13)

式中： $\phi$ 为受雷曲面边界与竖直方向的最大夹角； $\psi$ 满足几何关系 $\psi = {\text{π }}/2 - \theta$ 。联立式(11)与式(13)，可得：

${A_{{\text{eq1}}}} = \frac{1}{2}{R_{\text{s}}}^2\left[ {2\phi + {\text{π }} + \left( {\phi - {\text{π }}} \right)\cos \left( {2\phi } \right) - \frac{3}{2}\sin \left( {2\phi } \right)} \right]$

(14)

其中，

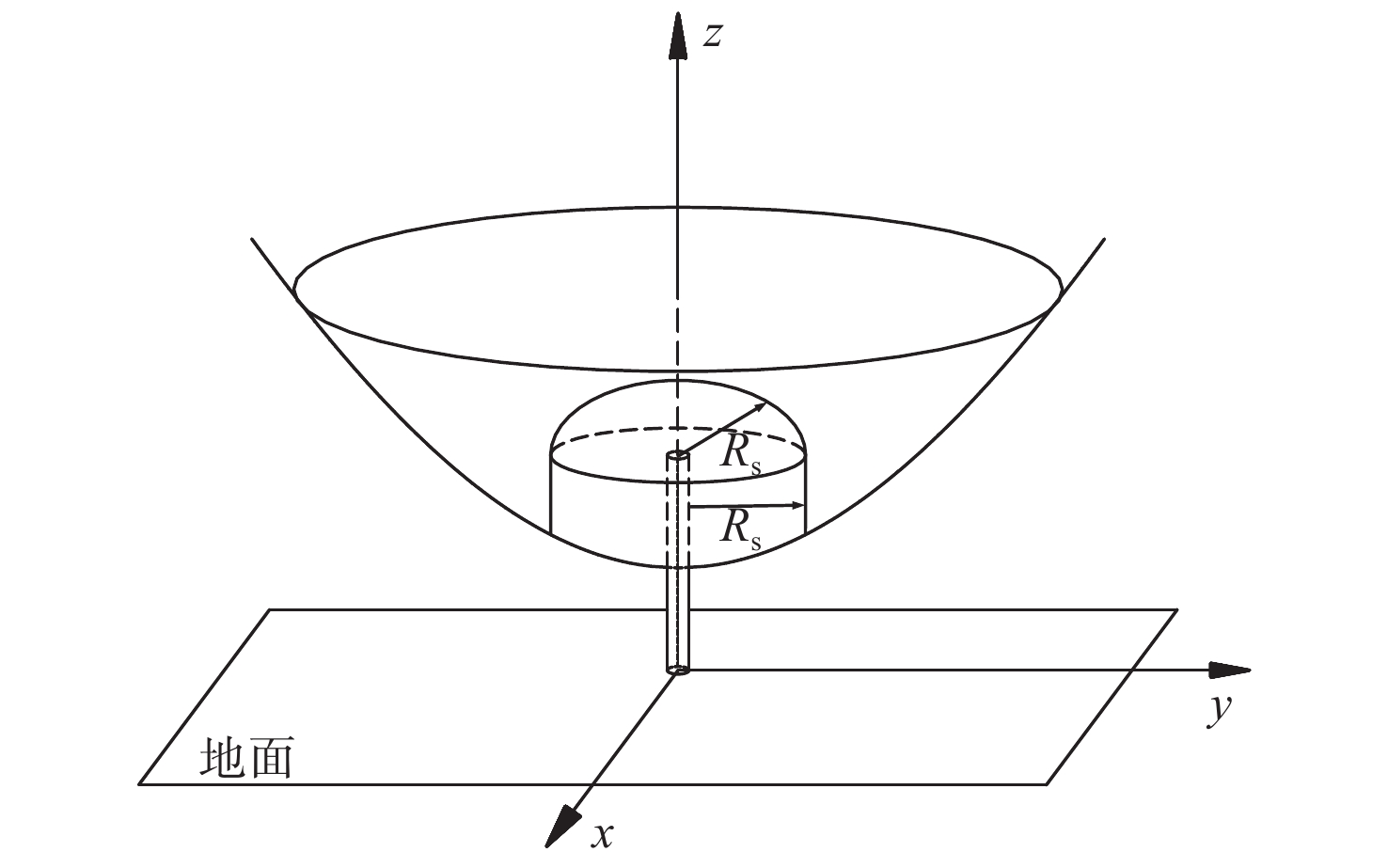
$\phi = \arctan \left( {\frac{{\sqrt {2{R_{\text{s}}}h - {h^2}} }}{{{R_{\text{s}}} - h}}} \right)$

(15)

值得注意的是，当雷击距 ${R_{\text{s}}}$ 小于避雷针高度h时，下行先导存在侧向击中避雷针的情况，其受雷曲面由半径为 ${R_{\text{s}}}$ 的半球面与圆柱面共同组成，如图5所示。此时雷电下行先导能量较小，存在侧向击中避雷针杆体的可能。该雷击距下避雷针的等效暴露面积可表示为

图 5 雷击距小于避雷针高度时的受雷曲面

Figure 5. Collection surface when the stroke distance is less than the height of lightning rod

下载: 全尺寸图片幻灯片

${A_{{\text{eq2}}}} = {A_{{\text{eq21}}}} + {A_{{\text{eq22}}}}$

(16)

式中， ${A_{{\text{eq21}}}}$ 和 ${A_{{\text{eq22}}}}$ 分别为半球面和圆柱面沿着下行先导入射方向的地面上的投影面积。

令式(14)中的 $\phi = {\text{π }}/2$ ，可得半球面沿下行先导方向在地面的投影面积，即

${A_{{\text{eq21}}}}{\text{ = }}\frac{{5{\text{π }}{R_{\text{s}}}^2}}{4}$

(17)

图6为圆柱面求解等效暴露面积的分解过程，同理，则有：

图 6 圆柱面等效暴露面积分解

Figure 6. Equivalent exposed area of cylinder surface

下载: 全尺寸图片幻灯片

${\text{d}}{A_2} = {R_{\text{s}}}{\text{d}}{\textit{z}}{\text{d}}\varphi$

(18)

${\text{d}}{A_{{\text{2L}}}} = {R_{\text{s}}}\sin \alpha {\text{d}}{\textit{z}}{\text{d}}\varphi$

(19)

${\text{d}}{A_{{\text{2G}}}} = \frac{{{R_{\text{s}}}\sin \alpha {\text{d}}{\textit{z}}{\text{d}}\varphi }}{{\cos \alpha }}$

(20)

同样，考虑到下行先导入射方向的随机性，可推导得到圆柱面的等效暴露面积为

${A_{{\text{eq22}}}} = \int_0^{\frac{{\text{π }}}{2}} {\left( {\int_0^{2{\text{π}}} {\int_{\frac{{{R_{\text{s}}}^2 + {h^2}}}{{2h}}}^h {\frac{{{R_{\text{s}}}\sin \alpha }}{{\cos \alpha }}{\text{d}}{\textit{z}}{\text{d}}\varphi } } } \right)} \cdot \frac{2}{\pi }{\cos ^2}\alpha {\text{d}}\alpha$

(21)

化简式(21)并联立式(17)，可得避雷针在小雷击距情况下的等效暴露面积为

${A_{{\text{eq2}}}} = \frac{{5{\text{π }}{R_{\text{s}}}^2}}{4} + 2{R_{\text{s}}}\left( {h - \frac{{{R_{\text{s}}}^2 + {h^2}}}{{2h}}} \right)$

(22)

综合上述分析，可得到全雷击距情况下的避雷针等效暴露面积为

${A_{\text{e}}} = \int_{{R_{{\text{s,min}}}}}^h {{A_{{\text{eq2}}}}f\left( {{R_{\text{s}}}} \right)} {\text{d}}{R_{\text{s}}} + \int_h^{{R_{{\text{s,max}}}}} {{A_{{\text{eq}}1}}f\left( {{R_{\text{s}}}} \right)} {\text{d}}{R_{\text{s}}}$

(23)

式中： ${R_{{\text{s,min}}}}$ 为可能的最小雷击距，通常取雷电流为1 kA时对应的雷击距大小； ${R_{{\text{s,max}}}}$ 为可能的最大击距，可取2～5 km。

联立式(7)和式(23)即可得到避雷针的预计雷击次数。为简化计算，假设某一区域的年预计雷击次数仅由高度最高的物体决定。架设避雷针前系统的预计雷击次数为N₁，该系统配置避雷针后，其预计雷击次数将仅由避雷针决定，即预计雷击次数增加至N₂，避雷针的存在导致其所在区域的引雷风险上升为原来的N_r倍：

${N_{\text{r}}} = \frac{{{N_2}}}{{{N_1}}}$

(24)

式中，N_r为反映避雷针引雷风险的量化表达式。

2.2 避雷针的拦截性能

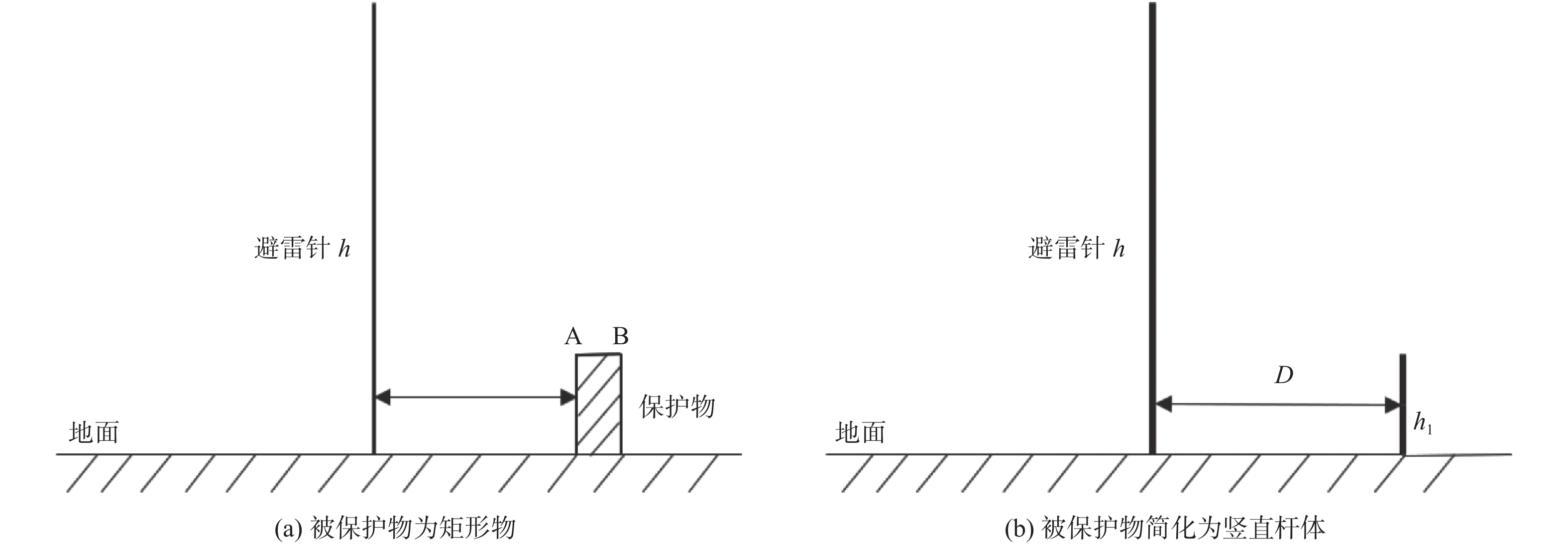
在雷电下行先导的发展过程中，避雷针与保护物存在着上行先导的竞争过程，上行先导产生时间及其发展速度的快慢，一定程度上决定了避雷针最终能否及时拦截下行先导。以图7(a)所示的简单避雷针防护系统为例，在雷电下行先导向地面发展的过程中，避雷针顶点、保护物顶点A和B均有可能产生上行先导，三者上行先导的竞争决定了最终的雷击点。为使本文所述方法具有通用性，可选取保护物的薄弱点为对象，研究避雷针对该点的防护概率，形式设为与该点等高的棒状尖端杆体，将问题转化为研究避雷针对该杆体的雷电拦截概率。将此防雷系统简化为图7(b)的避雷针−杆体系统，其中杆体顶点与保护物B点重合，避雷针对杆体的拦截效能等同于对保护物位置B的拦截效能。图中，h，h₁分别为避雷针和杆体的高度；D为二者间距。考虑到问题的轴对称性质，本节采用二维结构研究避雷针的拦截特性。

图 7 避雷针防雷系统示意图

Figure 7. Schematic diagram of lightning rod protection system

下载: 全尺寸图片幻灯片

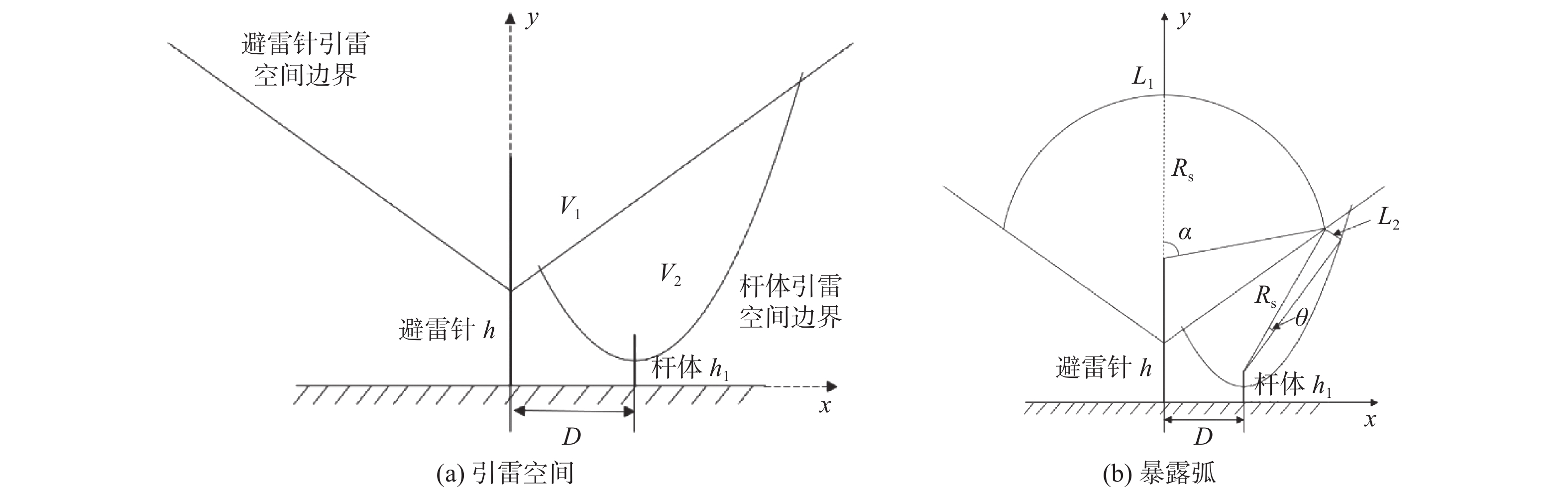
根据引雷空间理论同样可以得到避雷针在保护物（杆体）影响下的引雷空间，如图8(a)所示，引雷空间V₁内的雷电定向点在符合相应的雷击距条件下将会被避雷针拦截。以避雷针底部为原点建立直角坐标系，避雷针对杆体的引雷空间边界线满足

图 8 避雷针−杆体系统引雷空间与暴露弧

Figure 8. Attractive volume and exposure arc of lightning rod-mast system

下载: 全尺寸图片幻灯片

$x{\text{ = }}\frac{{2\left( {h - {h_1}} \right)y + {h_1}^2 - {h^2} + {D^2}}}{{2D}}$

(25)

杆体对地面的引雷空间边界线满足

$x = \sqrt {2{h_1}y - {h_1}^2} + D$

(26)

以避雷针和杆体顶点为圆心，雷击距 ${R_{\text{s}}}$ 为半径做圆弧，得到避雷针−杆体系统的暴露弧，如图8(b)所示。暴露弧L₁认为雷击距为 ${R_{\text{s}}}$ 的雷电下行先导头部到达该弧面时，将会击中避雷针，同理，下行先导头部位于弧面L₂时，将会击中杆体，此时认为避雷针拦截失效。

设下行先导头部落在弧面L₁，L₂任意位置的概率相等，则可据此估算避雷针在雷击距为 ${R_{\text{s}}}$ 情况下的拦截概率为

${P_{R = {R_{\text{s}}}}} = f\left( {{R_{\text{s}}}} \right) \cdot \frac{{{C_1}\left( {{R_{\text{s}}}} \right)}}{{{C_1}\left( {{R_{\text{s}}}} \right) + {C_2}\left( {{R_{\text{s}}}} \right)}}$

(27)

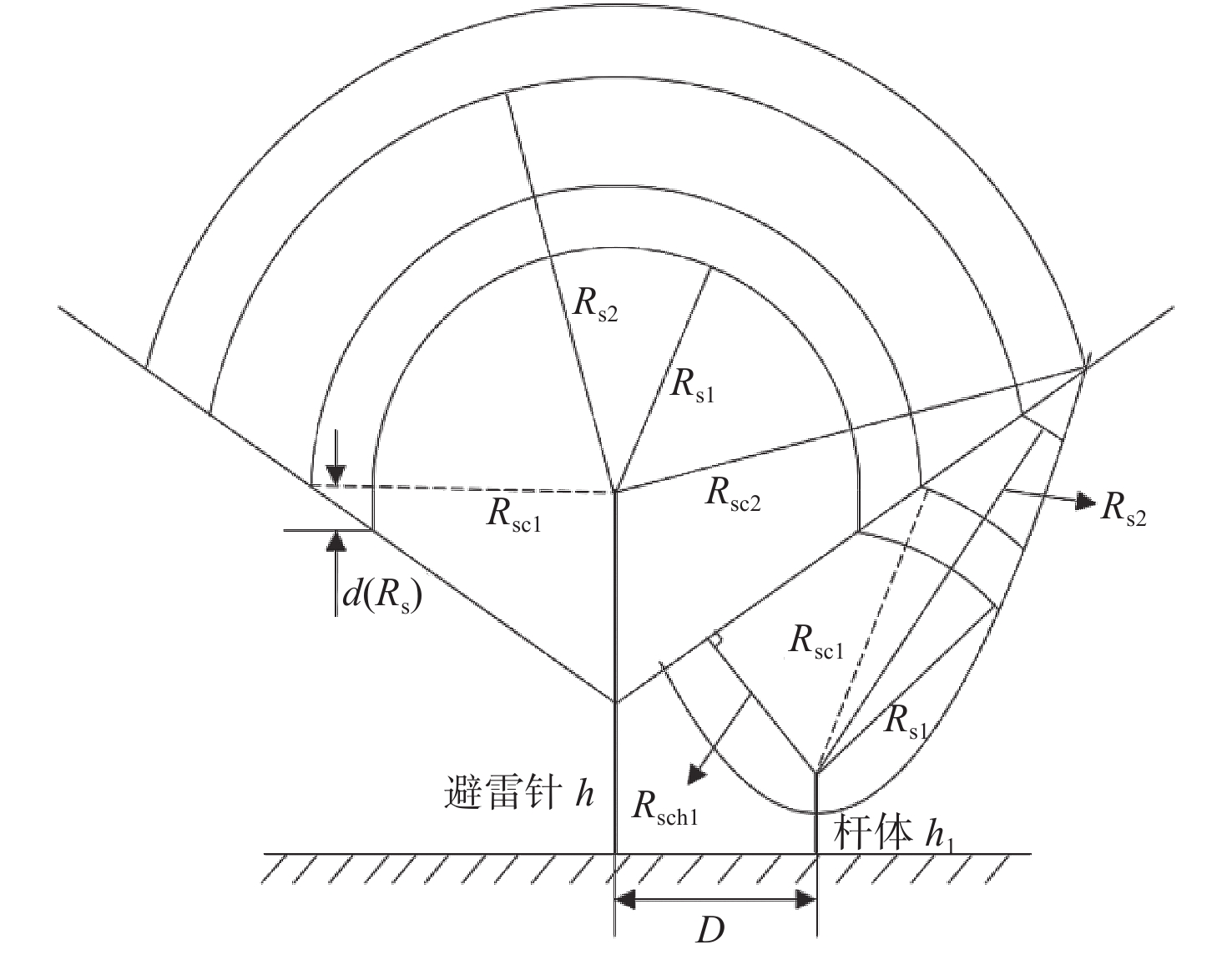
式中： ${C_1}\left( {{R_{\text{s}}}} \right)$ 和 ${C_2}\left( {{R_{\text{s}}}} \right)$ 分别为在雷击距为 ${R_{\text{s}}}$ 时避雷针和杆体的暴露弧弧长； $f\left( {{R_{\text{s}}}} \right)$ 为雷击距为 ${R_{\text{s}}}$ 的概率。

当携带不同能量的雷电下行先导（以雷击距表示）入射到避雷针−杆体系统时存在几种临界状态，如图9所示，图中， ${R_{{\text{sc}}1}}$ 为雷电先导恰有可能击中避雷针或杆体的击距， ${R_{{\text{sc2}}}}$ 为雷电先导恰无法击中杆体的击距， ${R_{{\text{sch1}}}}$ 为雷电先导恰无法被避雷针拦截的击距。当 ${R_{\text{s}}} < {R_{{\text{sc}}1}}$ 时，雷电下行先导可能存在侧击避雷针的情况；当 ${R_{\text{s}}} \geqslant {R_{{\text{sc2}}}}$ 时，杆体的暴露弧为0，即对于雷击距在 ${R_{{\text{sc2}}}}$ 以上的雷电下行先导，避雷针都能有效拦截，从而保护杆体免受直击雷损害；当 ${R_{\text{s}}} \leqslant {R_{{\text{sch1}}}}$ 时，避雷针的存在不再对杆体的暴露弧造成影响，即避雷针对杆体的防护概率为零。

图 9 避雷针−杆体系统在不同雷击距下的暴露弧

Figure 9. Exposure arc of lightning rod-mast system with different stroke distances

下载: 全尺寸图片幻灯片

因此，避雷针对杆体的拦截概率 ${P_{{\text{s}}}}$ 为

${P_{{\text{s}}}} = \left\{ \begin{aligned} & \int_{{R_{{\text{sch1}}}}}^{{R_{{\text{sc1}}}}} {\frac{{{C_{11}}\left( {{R_{\text{s}}}} \right)}}{{{C_{11}}\left( {{R_{\text{s}}}} \right) + {C_{21}}\left( {{R_{\text{s}}}} \right)}}f\left( {{R_{\text{s}}}} \right)} {\text{d}}{R_{\text{s}}} + \int_{{R_{{\text{sc1}}}}}^{{R_{{\text{sc2}}}}} {\frac{{{C_{12}}\left( {{R_{\text{s}}}} \right)}}{{{C_{12}}\left( {{R_{\text{s}}}} \right) + {C_{22}}\left( {{R_{\text{s}}}} \right)}}f\left( {{R_{\text{s}}}} \right)} {\text{d}}{R_{\text{s}}} + \int_{{R_{{\text{sc2}}}}}^{{R_{{\text{s,max}}}}} {f\left( {{R_{\text{s}}}} \right)} {\text{d}}{R_{\text{s}}},\;\;\;\;{R_{{\text{sch1}}}} < {R_{{\text{sc1}}}} \\& \int_{{R_{{\text{sch}}1}}}^{{R_{{\text{sc2}}}}} {\frac{{{C_{12}}\left( {{R_{\text{s}}}} \right)}}{{{C_{12}}\left( {{R_{\text{s}}}} \right) + {C_{22}}\left( {{R_{\text{s}}}} \right)}}f\left( {{R_{\text{s}}}} \right)} {\text{d}}{R_{\text{s}}} + \int_{{R_{{\text{sc2}}}}}^{{R_{{\text{s,max}}}}} {f\left( {{R_{\text{s}}}} \right)} {\text{d}}{R_{\text{s}}},\;\;\qquad\qquad\qquad\qquad\qquad\qquad\qquad{R_{{\text{sch1}}}} \geqslant {R_{{\text{sc1}}}} \end{aligned}\right.$

(28)

式中： ${C_{11}}\left( {{R_{\text{s}}}} \right)$ 和 ${C_{21}}\left( {{R_{\text{s}}}} \right)$ 为 ${R_{{\text{sch1}}}} \leqslant {R_{\text{s}}} < {R_{{\text{sc1}}}}$ 时的避雷针和杆体的暴露弧弧长； ${C_{12}}\left( {{R_{\text{s}}}} \right)$ 和 ${C_{22}}\left( {{R_{\text{s}}}} \right)$ 为 ${R_{{\text{sc1}}}} \leqslant {R_{\text{s}}} \leqslant {R_{{\text{sc2}}}}$ 或 ${R_{{\text{sch1}}}} \leqslant {R_{\text{s}}} \leqslant {R_{{\text{sc2}}}}$ （ ${R_{{\text{sch1}}}} \geqslant {R_{{\text{sc1}}}}$ 情况下）时的避雷针和杆体的暴露弧弧长。其中， ${R_{{\text{sc1}}}}$ ， ${R_{{\text{sc2}}}}$ 和 ${R_{{\text{sch1}}}}$ 的取值分别为：

${R_{{\text{sc1}}}} = \frac{{{{\left( {h - {h_1}} \right)}^2} + {D^2}}}{{2D}}$

(29)

$\begin{split} & {R_{{\text{sc2}}}} = \{ [ {{D^2} + {{( {h - {h_1}} )}^2}} ] \cdot [ {h^4} + {h_1}^4 + {D^2}( {{h^2} + {h_1}^2} ) -\\&\quad 2{h^2}{h_1}^2 + 4D( {h + {h_1}} )[ {h{h_1} + ( {{D^2} + {{( {h - {h_1}} )}^2}} )}]^{1/2} + \\&\quad\qquad\qquad 6{D^2}h{h_1} ] \} ^{1/2}/[{{2{{( {h - {h_1}} )}^2}}}] \end{split}$

(30)

${R_{{\text{sch1}}}} = \frac{1}{2}\sqrt {{D^2} + {{\left( {h - {h_1}} \right)}^2}}$

(31)

当雷电存在侧向击中避雷针杆体的情况时，避雷针的暴露弧包括：

${C_{11}}\left( {{R_{\text{s}}}} \right) = C\left( {{L_1}} \right) + 2d\left( {{R_{\text{s}}}} \right)$

(32)

其中， $C\left( {{L_1}} \right)$ ， $d\left( {{R_{\text{s}}}} \right)$ 分别为：

$C\left( {{L_1}} \right) = {\text{π }}{R_{\text{s}}}$

(33)

$d\left( {{R_{\text{s}}}} \right) = \left\{ \begin{aligned} & h - \frac{{2D{R_{\text{s}}} + {h^2} - {h_1}^2 - {D^2}}}{{2\left( {h - {h_1}} \right)}},\;\;\;{R_{\text{s}}} > \frac{{{h_1}^2 + {D^2} - {h^2}}}{{2D}} \\& h,\;\;\;\;\;\;\;\;\qquad\qquad\qquad\qquad{R_{\text{s}}} \leqslant \frac{{{h_1}^2 + {D^2} - {h^2}}}{{2D}} \end{aligned} \right.$

(34)

杆体的暴露弧 ${C_{21}}\left( {{R_{\text{s}}}} \right)$ 可表示为

${C_{21}}\left( {{R_{\text{s}}}} \right) = \theta \left( {{R_{\text{s}}}} \right){R_{\text{s}}}{\text{ }}$

(35)

式中： $\theta \left( {{R_{\text{s}}}} \right)$ 为 ${R_{\text{s}}}$ 下杆体暴露弧L₂的圆心角，其大小可表示为

$\begin{split} & \theta ( {{R_{\text{s}}}} ) = \arccos \{ \{ ( {h - {h_1}} ) \{({{4{R_{\text{s}}}^2}})/\\& [{{{D^2} + {{( {h - {h_1}} )}^2}}}] - 1\}^{1/2} - D \}/2{R_{\text{s}}} \} -\\& \arccos \{ {[{{ ({2{R_{\text{s}}}{h_1} - {h_1}^2})^{1/2} }}]/{{{R_{\text{s}}}}}} \} \end{split}$

(36)

当雷电不存在侧击情况时，避雷针的暴露弧弧长可表示为

${C_{12}}\left( {{R_{\text{s}}}} \right) = 2\alpha \left( {{R_{\text{s}}}} \right) \cdot {R_{\text{s}}}$

(37)

其中， $\alpha \left( {{R_{\text{s}}}} \right)$ 如图8(b)所示，表示在 ${R_{\text{s}}}$ 下避雷针暴露弧L₁的1/2圆心角：

$\begin{split} & \alpha ( {{R_{\text{s}}}} ) = \arccos \{ \{D \cdot ([ {{D^2} + {{( {h - {h_1}} )}^2}} ] \cdot [ 4{R_{\text{s}}}^2 -\\& {D^2} - {{( {h - {h_1}} )}^2} ])^{1/2} + ( {{h_1} - h} ) \cdot [ {D^2} + {{( {h - {h_1}} )}^2} ]\}/\\& \{{2{R_{\text{s}}}[ {{D^2} + {{( {h - {h_1}} )}^2}} ]}\} \} \end{split}$

(38)

杆体的暴露弧弧长 ${C_{22}}\left( {{R_{\text{s}}}} \right)$ 可表示为

${C_{22}}\left( {{R_{\text{s}}}} \right) = \theta \left( {{R_{\text{s}}}} \right){R_{\text{s}}}{\text{ }}$

(39)

由于避雷针对杆体的雷电拦截概率 ${P_{{\text{s}}}}$ 是关于 ${R_{\text{s}}}$ 的积分，一般难以求出其解析表达式，需要进行数值积分。

2.3 避雷针综合防护概率

基于上述研究得出的反映避雷针引雷、拦截特性的量化表达式，可以实现避雷针防护概率的高效计算。避雷针等高结构体的引入势必会增加系统的引雷风险，即N_r总是为大于1的常数，由于每两次雷击的发生属于相互独立事件，考虑避雷针带来的引雷风险后，其综合防护概率分布可近似认为属于二项分布，对空间任一点的综合防护概率 ${P_{{\text{p}}}}$ 可归纳为

${P_{{\text{p}}}} = {\left( {{P_{{\text{s}}}}} \right)^{{N_{\text{r}}}}}$

(40)

3. 算例分析

将本文提出的避雷针防护概率数值评估方法在Matlab中编制计算程序，可以实现避雷针对空间任意点的防护概率计算。为验证本文方法的准确性，以图7(b)的避雷针−杆体系统为例，分析避雷针防护概率的一般规律，并与现有文献中的结论进行对比。

为使本文方法的计算结果具有对比性，电气几何模型中雷击距与雷电流幅值关系式(1)的系数a，b取较多学者的推荐值，即a=10，b=0.65^[19]。雷电流幅值概率密度函数式(2)采用IEEE推荐形式，即 $\eta {\text{ = }}2.56$ ， ${I_0}{\text{ = }}31{\text{ kA}}$ ^[5]。

3.1 防护概率随避雷针高度的变化规律

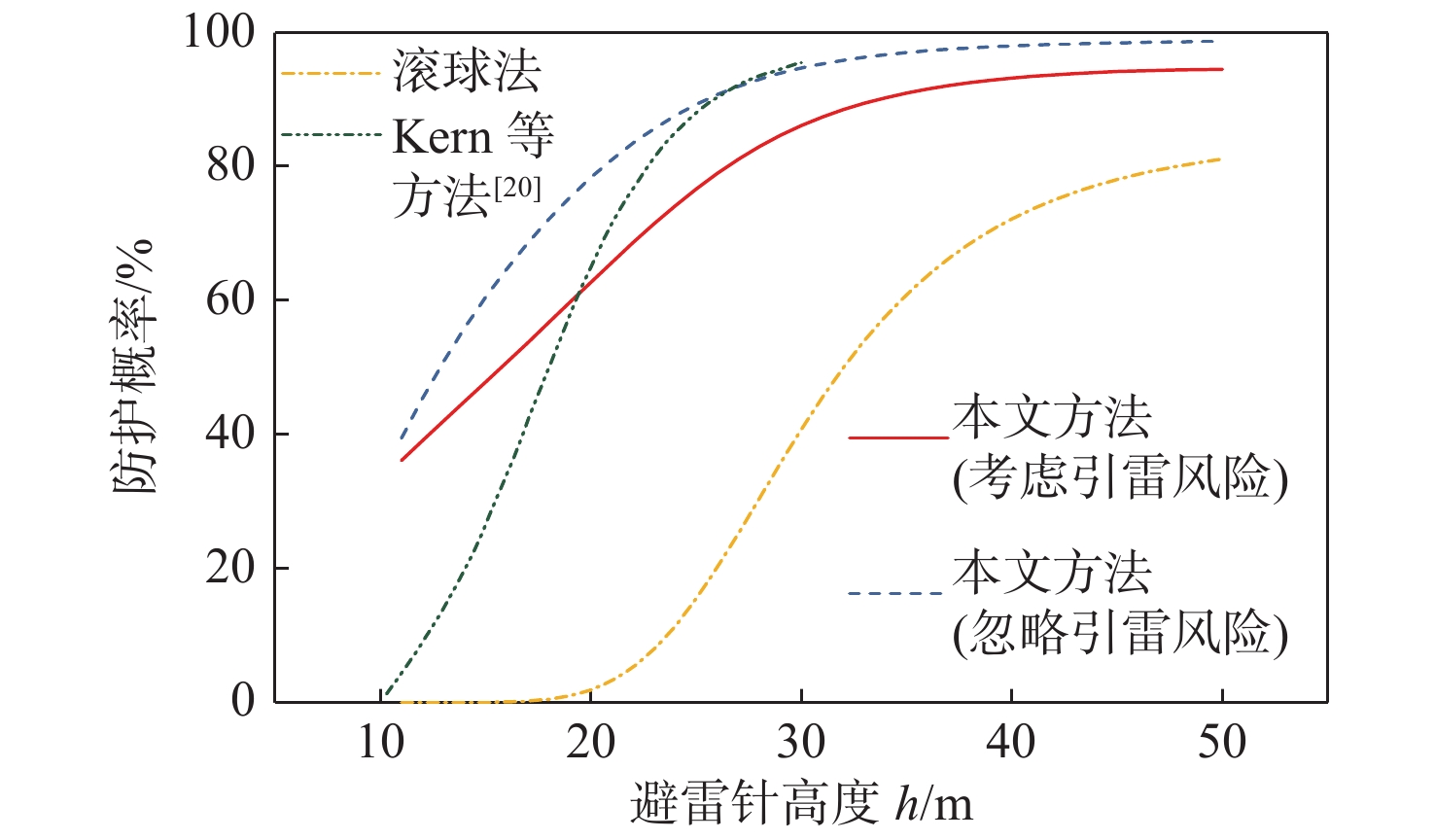
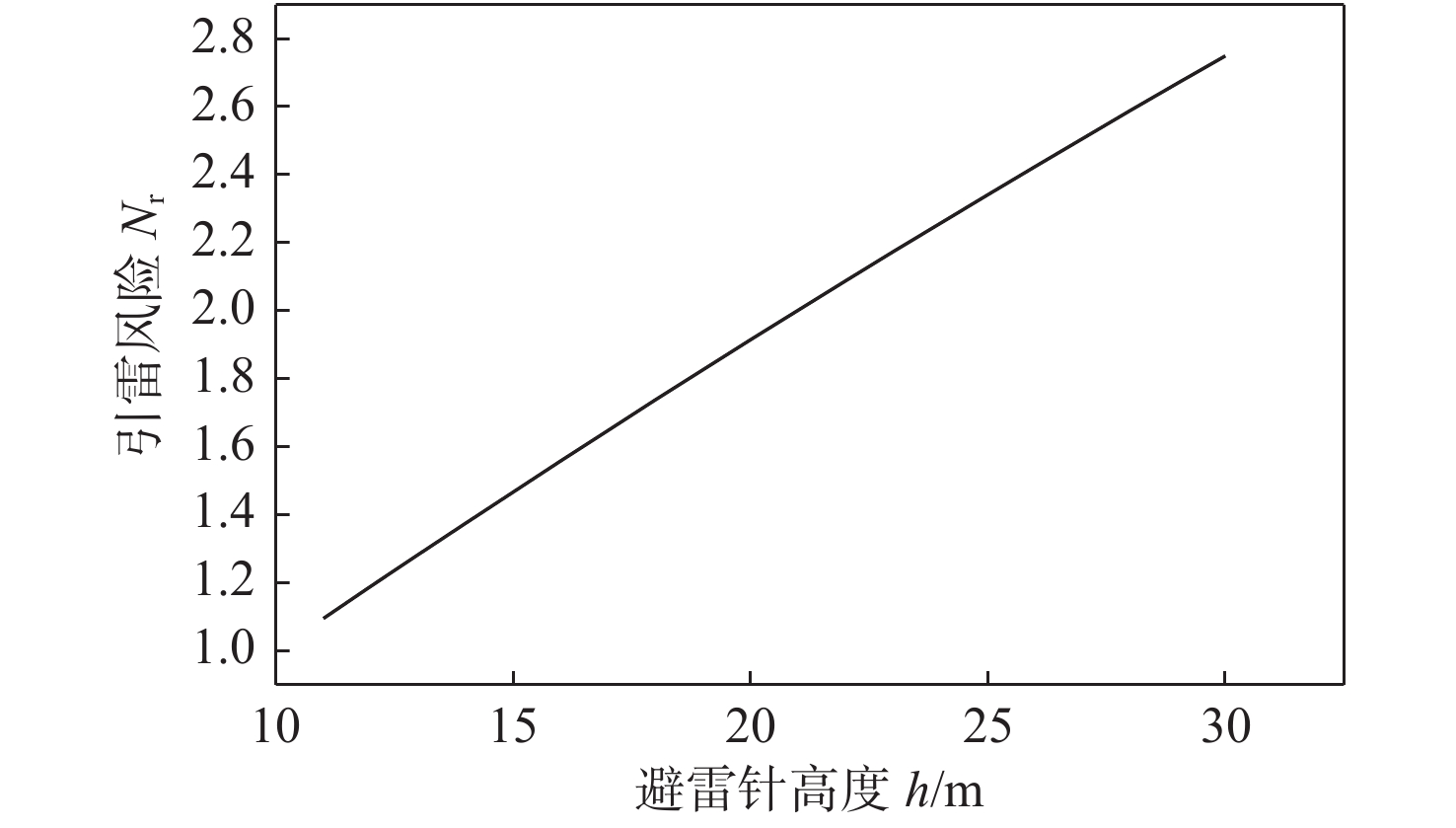
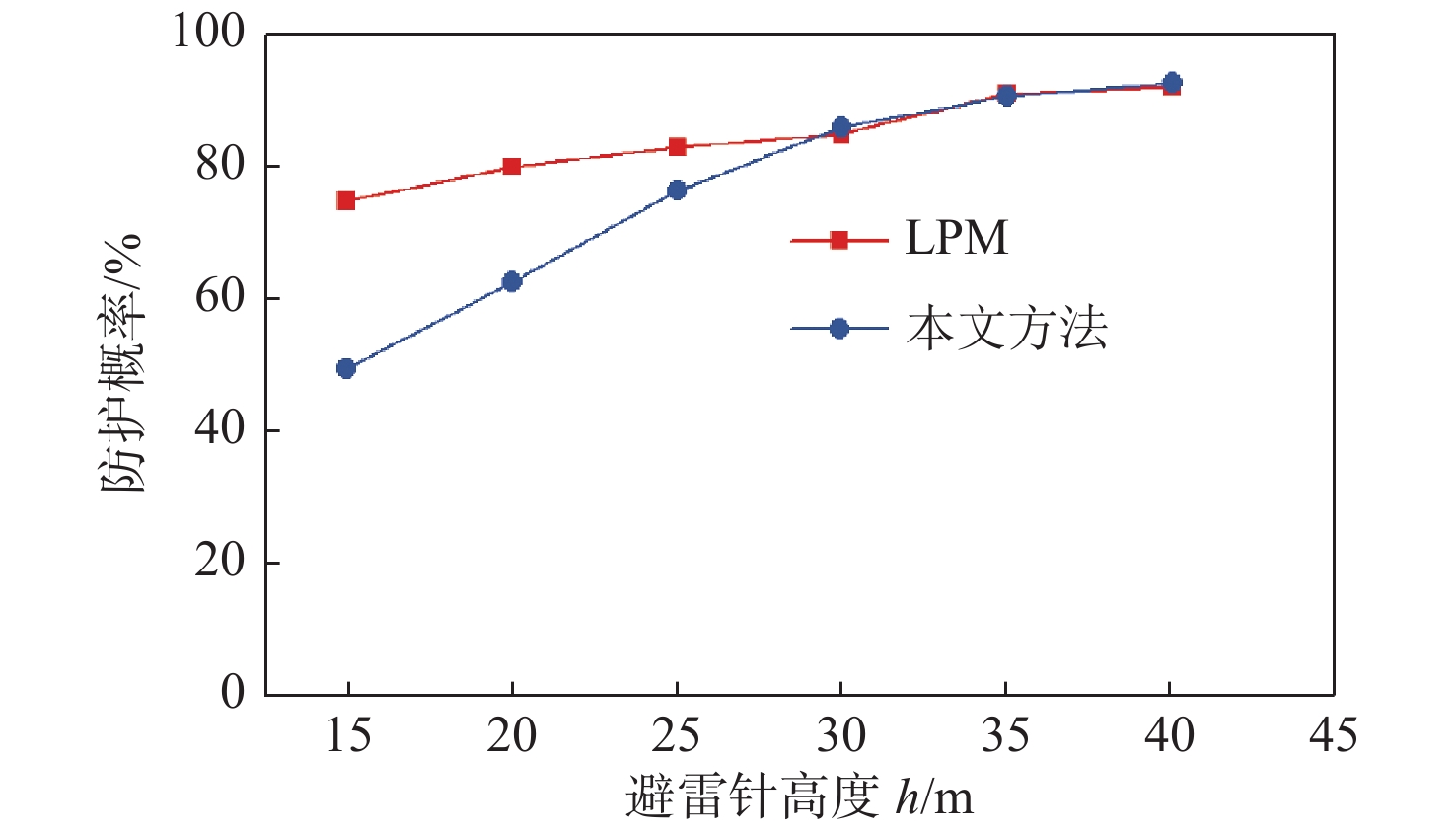
Kern等^[20]在滚球法的基础上研究了避雷针的防护概率随其高度的变化规律，为方便对比分析，本文设杆体高度h₁=10 m，与避雷针水平间距 $D{\text{ = }}20\sqrt 2 {\text{ m}}$ ，保持避雷针与杆体位置不变，逐渐增加避雷针高度，得到的避雷针防护概率随针高变化曲线如图10所示。

图 10 避雷针防护概率随针高的变化曲线

Figure 10. Variation of protection probability with the height of lightning rod

下载: 全尺寸图片幻灯片

比较各评估方法的避雷针防护概率随针高变化的曲线可得，随着避雷针高度的增加，防护概率呈上升趋势。滚球法未考虑上行先导对雷电的拦截作用，评估结果较严格，其防护概率值处于较低水平。因文献[20]是基于滚球法得出的避雷针防护概率变化曲线，而且未考虑避雷针带来的引雷风险，在避雷针较高时与本文方法忽略引雷风险下的防护概率曲线较为吻合。但避雷针的引雷风险与针高近似呈线性正相关，往往是不可忽略的（图11）。本文方法在针高较低时具有较为宽松的评估结果，在避雷针较高时能充分考虑到其所带来的引雷风险，防护概率随针高的增加不至太高，总体概率变化趋势与其他分析方法相符。

图 11 引雷风险随避雷针针高度的变化曲线

Figure 11. Variation of attractive risk with the height of lightning rod

下载: 全尺寸图片幻灯片

3.2 单避雷针的保护范围

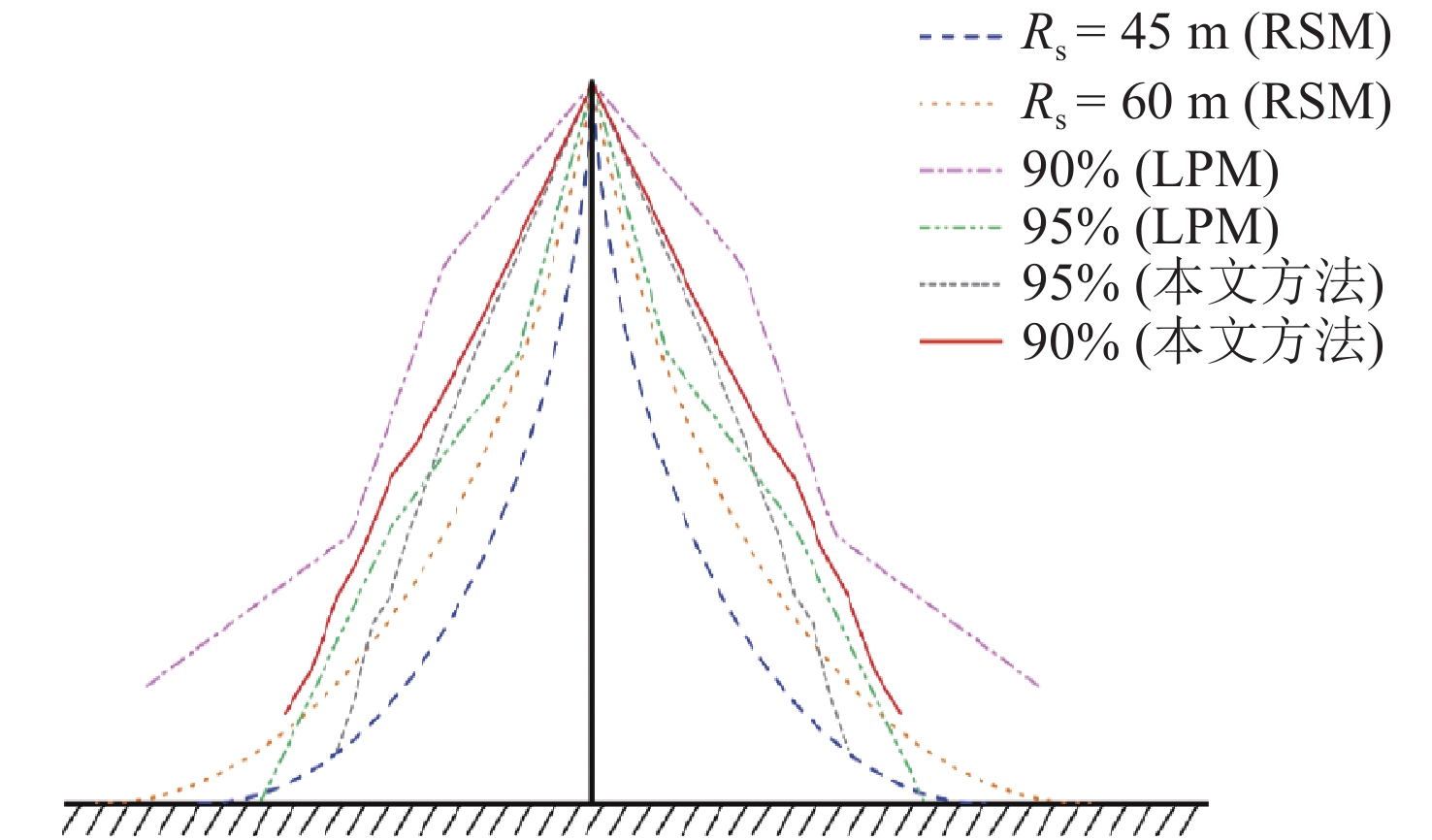
避雷针的保护范围一直是防雷系统设计的关键参考参数，将本文提出的避雷针数值评估方法运用于保护范围的研究，对40 m高的避雷针绘制等概率保护范围边界线，并与RSM和LPM方法^[11]的评估结果进行对比分析，结果如图12所示。

图 12 不同防护效能的避雷针保护范围与RSM和LPM方法对比结果

Figure 12. Protection range of lightning rod with different effectiveness and comparisons with the evaluation results by RSM and LPM

下载: 全尺寸图片幻灯片

图中基于RSM的保护范围（ ${R_{\text{s}}}{\text{ = }}45{\text{ m}}$ 时对应的防护概率约为95%， ${R_{\text{s}}}{\text{ = }}60{\text{ m}}$ 时对应的防护概率约为85%）均远小于本文方法和LPM评估的保护范围大小，与本文前述分析结果相同，具有最为严格的评估结果。本文方法计算得到的95%与90%保护范围边界线分布在LPM相应的两条边界线之间，且相差不大，与LPM仿真结果较为吻合。

3.3 防护概率数值评估结果与LPM方法的对比

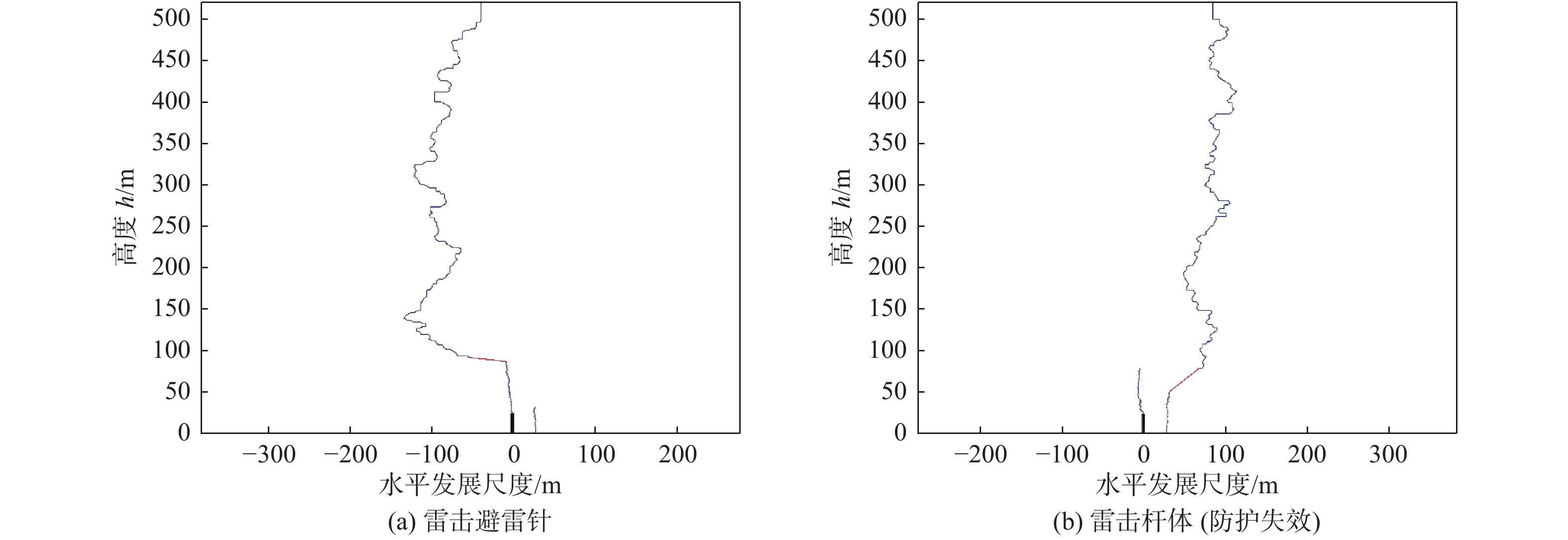
现有的量化评估避雷针防护概率方法多采用LPM多次模拟雷击过程，将击中避雷针的次数与总次数之比作为避雷针的防护概率。因此，为进一步说明本文方法的准确性和高效性，本文仍设杆体高度h₁=10 m，与避雷针水平间距D= $20\sqrt 2 {\text{ m}}$ ，保持避雷针与杆体位置不变，逐渐增加避雷针高度，每种避雷针的配置均在LPM^[12]中进行100次雷击模拟，典型仿真结果如图13所示。得到LPM方法的避雷针防护概率统计结果，并与本文方法理论评估结果进行比较，如表1所示。

图 13 LPM仿真结果

Figure 13. Simulation results of LPM

下载: 全尺寸图片幻灯片

表 1 避雷针防护概率评估结果与计算效率

Table 1. Evaluation results and calculation efficiency of lightning rod protection probability

避雷针高度/m	LPM		本文方法
避雷针高度/m	防护概率P₁/%	平均耗时/min	防护概率P₂/%	平均耗时/s
15	75	45	49.79	<1
20	80	45	62.69	<1
25	83	45	76.56	<1
30	85	45	85.93	<1
35	91	45	90.64	<1
40	92	45	92.66	<1

下载: 导出CSV

| 显示表格

根据表1与图14的分析结果，采用LPM进行避雷针防护概率的数值评估时，在高性能计算平台上单次评估耗时（100次雷击模拟）约45 min，远大于本文方法的计算耗时，即本文方法的效率远优于LPM。与LPM的评估结果相比，本文方法的防护概率变化趋势与LPM的趋势相似，数值上也具有较高的吻合度。即本文方法的评估结果效果好且效率高，可作为避雷针防护概率数值评估工具。

图 14 本文方法与LPM的避雷针防护概率评估结果对比

Figure 14. Comparison of lightning rod protection probability evaluation results obtained by the method in this paper and LPM

下载: 全尺寸图片幻灯片

4. 结　论

本文基于电气几何模型与引雷空间理论，将雷击物理过程转化为电气几何问题，对避雷针的引雷风险与雷电拦截性能进行了理论分析，建立了避雷针防护概率数值评估方法，得到以下结论：

1）根据电气几何模型及引雷空间理论建立了避雷针引雷空间与受雷曲面，将其受雷曲面在下行先导方向上在地面的投影面积等效为截收相同雷击次数的等效暴露面积，通过对比避雷针引入前后系统的预计雷击次数变化，实现对避雷针引雷风险的量化评估。

2）将空间待求点以等高杆体替代来等效分析避雷针对该点的雷电拦截性能，通过分析避雷针与杆体上行先导的竞争关系建立系统的引雷空间，对比不同雷击距的下行先导作用下避雷针与杆体的暴露弧分布情况，实现对避雷针雷电拦截特性的量化评估。

3）综合避雷针引雷与防雷两方面特性来实现对避雷针防护概率的数值评估，并将该评估方法与国内外学者的研究结论进行对比分析，证明了该方法的准确性与可行性；且该方法量化程度高，可通过计算机编程实施计算，进而实现避雷针对空间任一点防护概率的高效计算。

图 1 避雷针的引雷示意图

Figure 1. Schematic diagram of conducting the lightning to the ground via lightning rod

下载: 全尺寸图片幻灯片

图 2 避雷针引雷空间边界

Figure 2. The atrractive volume boundary of lightning rod

下载: 全尺寸图片幻灯片

图 3 避雷针在雷击距为R_s时的受雷曲面

Figure 3. Collection surface of lightning rod at the stroke distance of R_s

下载: 全尺寸图片幻灯片

图 4 避雷针等效暴露面积计算方法

Figure 4. Calculation method of equivalent exposure area of lightning rod

下载: 全尺寸图片幻灯片

图 5 雷击距小于避雷针高度时的受雷曲面

Figure 5. Collection surface when the stroke distance is less than the height of lightning rod

下载: 全尺寸图片幻灯片

图 6 圆柱面等效暴露面积分解

Figure 6. Equivalent exposed area of cylinder surface

下载: 全尺寸图片幻灯片

图 7 避雷针防雷系统示意图

Figure 7. Schematic diagram of lightning rod protection system

下载: 全尺寸图片幻灯片

图 8 避雷针−杆体系统引雷空间与暴露弧

Figure 8. Attractive volume and exposure arc of lightning rod-mast system

下载: 全尺寸图片幻灯片

图 9 避雷针−杆体系统在不同雷击距下的暴露弧

Figure 9. Exposure arc of lightning rod-mast system with different stroke distances

下载: 全尺寸图片幻灯片

图 10 避雷针防护概率随针高的变化曲线

Figure 10. Variation of protection probability with the height of lightning rod

下载: 全尺寸图片幻灯片

图 11 引雷风险随避雷针针高度的变化曲线

Figure 11. Variation of attractive risk with the height of lightning rod

下载: 全尺寸图片幻灯片

图 12 不同防护效能的避雷针保护范围与RSM和LPM方法对比结果

Figure 12. Protection range of lightning rod with different effectiveness and comparisons with the evaluation results by RSM and LPM

下载: 全尺寸图片幻灯片

图 13 LPM仿真结果

Figure 13. Simulation results of LPM

下载: 全尺寸图片幻灯片

图 14 本文方法与LPM的避雷针防护概率评估结果对比

Figure 14. Comparison of lightning rod protection probability evaluation results obtained by the method in this paper and LPM

下载: 全尺寸图片幻灯片

表 1 避雷针防护概率评估结果与计算效率

Table 1 Evaluation results and calculation efficiency of lightning rod protection probability

避雷针高度/m LPM 本文方法
防护概率P₁/% 平均耗时/min 防护概率P₂/% 平均耗时/s

15 75 45 49.79 <1
20 80 45 62.69 <1
25 83 45 76.56 <1
30 85 45 85.93 <1
35 91 45 90.64 <1
40 92 45 92.66 <1

下载: 导出CSV

参考文献(20)

[1]	电力工业部科学技术司. 交流电气装置的过电压保护和绝缘配合: DL/T 620—1997[S]. 北京: 中国电力出版社, 1997. Ministry of Electric Power Industry of the People's Republic of China. Overvoltage protection and insulation coordination for AC electrical installations: DL/T 620-1997[S]. Beijing: China Electric Power Press, 1997 (in Chinese).
[2]	中华人民共和国住房和城乡建设部. 交流电气装置的过电压保护和绝缘配合设计规范: GB/T 50064—2014[S]. 北京: 中国计划出版社, 2014. Ministry of Housing and Urban-rural Development of the People's Republic of China. Code for design of overvoltage protection and insulation coordination for AC electrical installations: GB/T 50064-2014[S]. Beijing: China Planning Press, 2014 (in Chinese).
[3]	BRUSSO B. The electrogeometrical model of the rolling sphere method[J]. IEEE Industry Applications Magazine, 2016, 22(2): 7–70. doi: 10.1109/MIAS.2015.2503940
[4]	GOLDE R H. The frequency of occurrence and the distribution of lightning flashes to transmission lines[J]. Transactions of the American Institute of Electrical Engineers, 1945, 64(12): 902–910. doi: 10.1109/T-AIEE.1945.5059060
[5]	Substations Committee of the IEEE Power Engineering Society. IEEE guide for direct lightning stroke shielding of substations: IEEE Std 998-1996[S]. New York: American National Standards Institute, 1996.
[6]	LEE R H. Lightning protection of buildings[J]. IEEE Transactions on Industry Applications, 1979, IA-15(3): 236–240. doi: 10.1109/TIA.1979.4503648
[7]	DELLERA L, GARBAGNATI E. Lightning stroke simulation by means of the leader progression model. I. Description of the model and evaluation of exposure of free-standing structures[J]. IEEE Transactions on Power Delivery, 1990, 5(4): 2009–2022. doi: 10.1109/61.103696
[8]	ERIKSSON A J, MOUSA A M. Discussion of "Lightning stroke simulation by means of the leader progression model. II. Exposure and shielding failure evaluation of overhead lines with assessment of application graphs" by L. Dellera and E. Garbagnati (and replies)[J]. IEEE Transactions on Power Delivery, 1991, 6(1): 456–460. doi: 10.1109/61.103771
[9]	RIZK F A M. Modeling of transmission line exposure to direct lightning strokes[J]. IEEE Transactions on Power Delivery, 1990, 5(4): 1983–1997. doi: 10.1109/61.103694
[10]	RIZK F A M. Switching impulse strength of air insulation: leader inception criterion[J]. IEEE Transactions on Power Delivery, 1989, 4(4): 2187–2195. doi: 10.1109/61.35646
[11]	ZHANG X W, DONG L, HE J L, et al. Study on the effectiveness of single lightning rods by a fractal approach[J]. Journal of Lightning Research, 2009, 1(1): 1–8. doi: 10.2174/1652803400901010001
[12]	GUO J, ZHANG X D, WANG B Y, et al. A three-dimensional direct lightning strike model for lightning protection of the substation[J]. IET Generation, Transmission & Distribution, 2021, 15(19): 2760–2772.
[13]	万浩江, 魏光辉, 陈亚洲, 等. 雷电先导放电通道内电场和电荷的分布特征[J]. 中国舰船研究, 2015, 10(2): 55–59,64. doi: 10.3969/j.issn.1673-3185.2015.02.010 WAN H J, WEI G H, CHEN Y Z, et al. Distribution features of the electric field and charge density in the lightning leader channel[J]. Chinese Journal of Ship Research, 2015, 10(2): 55–59,64 (in Chinese). doi: 10.3969/j.issn.1673-3185.2015.02.010
[14]	ERIKSSON A J. An improved electrogeometric model for transmission line shielding analysis[J]. IEEE Transactions on Power Delivery, 1987, 2(3): 871–886. doi: 10.1109/TPWRD.1987.4308192
[15]	DELLERA L, GARBAGNATI E. Lightning stroke simulation by means of the leader progression model. II. Exposure and shielding failure evaluation of overhead lines with assessment of application graphs[J]. IEEE Transactions on Power Delivery, 1990, 5(4): 2023–2029. doi: 10.1109/61.103697
[16]	中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局. 建筑物防雷设计规范: GB 50057—2010[S]. 北京: 中国计划出版社, 2011. Ministry of Housing and Urban-rural Development of the People's Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. Code for design protection of structures against lightning: GB 50057-2010[S]. Beijing: China Plans Press, 2011 (in Chinese).
[17]	张小青. 预测竖直杆体的年雷击率[J]. 电工技术学报, 2005, 20(3): 70–74. doi: 10.3321/j.issn:1000-6753.2005.03.013 ZHANG X Q. Prediction of the annual incidence of lightning strikes to erect masts[J]. Transactions of China Electrotechnical Society, 2005, 20(3): 70–74 (in Chinese). doi: 10.3321/j.issn:1000-6753.2005.03.013
[18]	GOLDE R H. Lightning[M]. New York: Academic Press, 1977: 225-226.
[19]	LOVE E R. Improvement on lightning stroke modelling and applications to design of EHV and UHV transmission lines[D]. Denver: University of Colorado, 1973.
[20]	KERN A, SCHELTHOFF C, MATHIEU M. Probability of lightning strikes to air-terminations of structures using the electro-geometrical model theory and the statistics of lightning current parameters[J]. Atmospheric Research, 2012, 117: 2–11. doi: 10.1016/j.atmosres.2011.01.009

施引文献(2)

期刊类型引用(2)

1.	张晓文，姚娟，张佳琳，董新伟. 基于PSCAD的采油区配电线路防雷研究. 电力大数据. 2024(02): 42-53 . 百度学术
2.	张旭东，陆佳骏，喻子颖，王帮勇，曹斌，郭俊，谢彦召. 基于雷电先导分形模型的舰船雷击风险研究. 中国舰船研究. 2023(04): 59-67 . 本站查看

其他类型引用(0)

资源附件(1)

其他相关附件
- 本文双语pdf
  ZG2483_en 点击下载(2897KB)

图(14) / 表(1)

计量

文章访问数: 540
HTML全文浏览量: 163
PDF下载量: 65
被引次数: 2

0. 引　言
1. 电气几何模型与引雷空间
1.1 电气几何模型
1.2 引雷空间
2. 避雷针防护概率数值评估方法
2.1 避雷针带来的引雷风险
2.2 避雷针的拦截性能
2.3 避雷针综合防护概率
3. 算例分析
3.1 防护概率随避雷针高度的变化规律
3.2 单避雷针的保护范围
3.3 防护概率数值评估结果与LPM方法的对比
4. 结　论

0. 引　言
1. 电气几何模型与引雷空间
1.1 电气几何模型
1.2 引雷空间
2. 避雷针防护概率数值评估方法
2.1 避雷针带来的引雷风险
2.2 避雷针的拦截性能
2.3 避雷针综合防护概率
3. 算例分析
3.1 防护概率随避雷针高度的变化规律
3.2 单避雷针的保护范围
3.3 防护概率数值评估结果与LPM方法的对比
4. 结　论

参考文献(20)

施引文献

资源附件(1)

避雷针防护概率数值评估方法

通讯作者: 郭俊

计量

出版历程

Numerical evaluation method of lightning rod protection probability

0. 引 言

1. 电气几何模型与引雷空间

1.1 电气几何模型

1.2 引雷空间

2. 避雷针防护概率数值评估方法

2.1 避雷针带来的引雷风险

2.2 避雷针的拦截性能

2.3 避雷针综合防护概率

3. 算例分析

3.1 防护概率随避雷针高度的变化规律

3.2 单避雷针的保护范围

3.3 防护概率数值评估结果与LPM方法的对比

4. 结 论

期刊类型引用(2)

其他类型引用(0)

其他相关附件

本文双语pdf

计量

出版历程

目录

0. 引 言

1. 电气几何模型与引雷空间

1.1 电气几何模型

1.2 引雷空间

2. 避雷针防护概率数值评估方法

2.1 避雷针带来的引雷风险

2.2 避雷针的拦截性能

2.3 避雷针综合防护概率

3. 算例分析

3.1 防护概率随避雷针高度的变化规律

3.2 单避雷针的保护范围

3.3 防护概率数值评估结果与LPM方法的对比

4. 结 论

通讯作者:
郭俊

0. 引　言

4. 结　论

0. 引　言

4. 结　论