Numerical study on hydrodynamic performance of ducted propeller based on improved body force model
-
摘要:目的 旨在解决传统Goldstein体积力法在导管螺旋桨水动力仿真中的适用局限性问题。方法 首先，基于机翼理论，分析导管水动力模拟失真的原因，并以质量流量和体积力分布模型为切入点，提出修正思想和方法；然后，采用RANS方法探究经质量流量修正后的2种体积力分布模型的模拟精度。结果 结果显示，2种改进体积力法在敞水工况下其总推力系数的平均相对误差均为5%左右；在艇后工况下，前进合力的平均相对误差分别为1.8%和11.6%。结论 研究表明，基于改进体积力法的导管螺旋桨在敞水和艇后工况下的模拟精度较传统体积力法有较大的提升，能准确实现对导管螺旋桨水动力性能的数值模拟，可为水下航行器高效、动态的操纵性仿真奠定基础。Abstract:Objectives The paper aims to solves the limitations of the Goldstein body force method in a hydrodynamic simulation of a ducted propeller.Methods An analysis of the reason for the distortion of the duct hydrodynamic simulation is carried out based on the wing theory, and a correction method based on the mass flow and body force distribution model is proposed. The RANS method is then used to study the simulation accuracy of two kinds of improved body force method.Results The results show that the average relative error of the total thrust coefficient of the two improved body force methods under open water conditions is about 5%. The average relative error of the resultant forward force of the two improved volume force methods behind the underwater vehicle are 1.8% and 11.6% respectively.Conclusions The simulation accuracy of a ducted propeller based on the improved body force method in open water and behind an underwater vehicle is greatly improved compared with the traditional method. The proposed method can accurately simulate the hydrodynamic performance of a ducted propeller, laying the foundation for the efficient dynamic maneuverability simulation of underwater vehicles.
-
0. 引 言
无论是遥控无人潜水器（remotely operated vehicle，ROV）还是自主水下航行器（autonomous underwater vehicle，AUV），都需要有良好的操纵性能，以便能按照预先的程序或是实时指令实现位姿变换，完成工作任务。随着计算机技术的飞速发展，计算流体力学（CFD）方法成为船舶操纵性领域的重要研究手段。采用CFD方法能够求解理论分析无法获得的复杂流动，且和物理试验相比，所需的人力、财力大为减少。但在多时间尺度物理场（例如，直升机飞行、船舶螺旋桨推进）模拟中，采用CFD方法往往十分耗时，故而体积力法（body force method，BFM）常被用于模拟桨叶的高速转动效应。
体积力法在不同的学科领域又可称作动量源法（momentum source method，MSM），或是鼓动盘理论[1]（actuator disk theory，ADT）。体积力法是将螺旋桨对流体的力等效为某种分布形式的力源项而输入N-S方程进行求解，既可减小网格数量和生成难度，又能缩小物理场时间尺度跨度，从而提高计算效率；当不需要流场详细的信息时，非常适合采用该方法进行潜艇操纵性评估[2-3]。Gaggero等[4]利用体积力法的高效计算效率，针对导管形状开展了快速设计和优化研究。何涛等[5]使用基于叶素理论的改进体积力法，对KCS船开展了回转运动仿真，所得精度令人满意。吴召华等[2]使用体积力分布模型，对KCS船进行了回转运动数值模拟。吴浩等[6]应用描述型体积力法开展了船舶自航数值研究，探究了虚拟桨的进流盘半径和偏移量对自由自航的影响。
目前，应用得最普遍的描述型体积力法是以Goldstein最佳环量分布为分布模型。该最佳环量分布始于Goldstein[7]因成功、精确地求解Betz基于势流升力线理论而提出的最佳环量分布条件问题。螺旋桨的性能与径向环量分布有关，吴家鸣等[8]的研究表明，Goldstein最佳环量分布不适用于导管螺旋桨。导管螺旋桨的水动力性模拟精度较普通螺旋桨低。Feng等[9]基于叶素理论，将采用CFD计算得到的桨盘面处当地速度场直接用于计算各半径处叶片的推力和扭矩，获得了与实体离散桨模型几乎相同的流场分布情形。郁程等[10]针对侧推器这种内部流动情形开展改进体积力法研究，提出了考虑转子阻塞影响的流量修正方法。Eslamdoost等[11]研究了3种体积力模型在轴流泵中的适用性，其中考虑了导叶、轴向均布体积力和周向体积力的体积力模型与多重参考系法（MRF）相比所得扬程的精度相当，喷口处的局部流场较MRF精度更高。Knight等[12]训练了一种半经验算法用于确定非定常螺旋桨体积力。宋长江等[13]采用叶素理论，对类似于水下导管螺旋桨的空气涵道尾桨开展了动量源法CFD分析，结果显示桨的推力值与试验值基本吻合。
当前，有关体积力法的改进研究层出，但聚焦于水下导管螺旋桨体积力法适用性及改进方法的研究较少。探究适用于导管螺旋桨的体积力法有利于在保证宏观运动精度的前提下提高水下航行器操纵运动模拟的效率。为解决传统体积力法在导管螺旋桨中的适用局限性问题，将首先基于机翼理论分析导管螺旋桨水动力模拟失真的原因，然后提出质量流量修正和分布修正这2种修正方法，最后在敞水和艇后这2种工况下探究2种体积力分布形式的模拟精度，并对改进的螺旋桨体积力模型进行数值验证，用以为搭配导管螺旋桨的水下航行器高效、准确的动态操纵性仿真奠定基础。
1. 数值模拟方法
本文采用RANS方法和STAR-CCM+平台求解器开展基于体积力法的导管螺旋桨水动力性能研究。
1.1 控制方程
对于三维定常、不可压缩的黏性流场，流体满足连续性方程和动量守恒方程：
∂ui∂xi=0 (1) uj∂(ui)∂xj=−1ρ∂p∂xi+(gi+fi)+μρ∂2ui∂xj∂xj−∂¯u′iu′j∂xj (2) 式中：xi，xj( i，j = 1，2，3)为坐标分量；ui，uj ( i，j = 1，2，3)为速度分量时均值；ρ为流体密度；p为压力时均值；gi，fi分别为重力加速度和自定义单位质量力在xi方向的分量；−¯u′iu′j为雷诺应力项；μ为动力黏性系数。雷诺平均应力张量采用经典的涡黏假设，并表达成Boussinsq建议的形式：
−ρ¯u′ju′i=μt(∂¯ui∂xj+∂¯uj∂xi)−23ρkδij (3) 式中：μt为湍流涡黏度；k为单位质量流体的湍流脉动动能；δij为克罗内克函数。采用适合进行潜艇操纵性数值计算的两方程模型，即剪切应力运输（shear-stress transport，SST）k - ω湍流模型封闭RANS方程，该模型对于附着边界层湍流和适度分离湍流均有着较高的计算精度[14]。湍动能k和单位耗散率ω的运输方程以及其中各参数的定义与取值参见文献[15-16]。
1.2 计算模型及网格划分
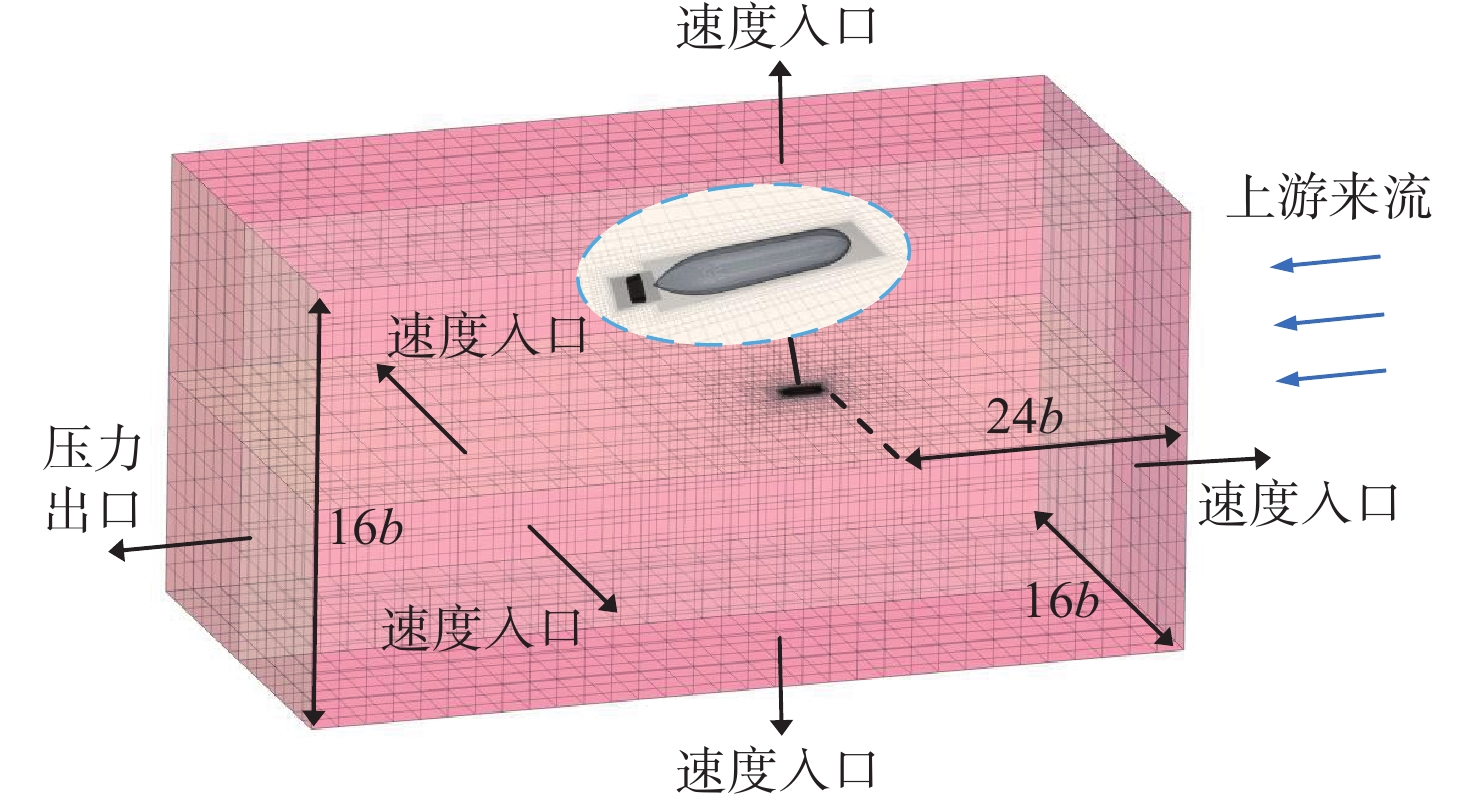
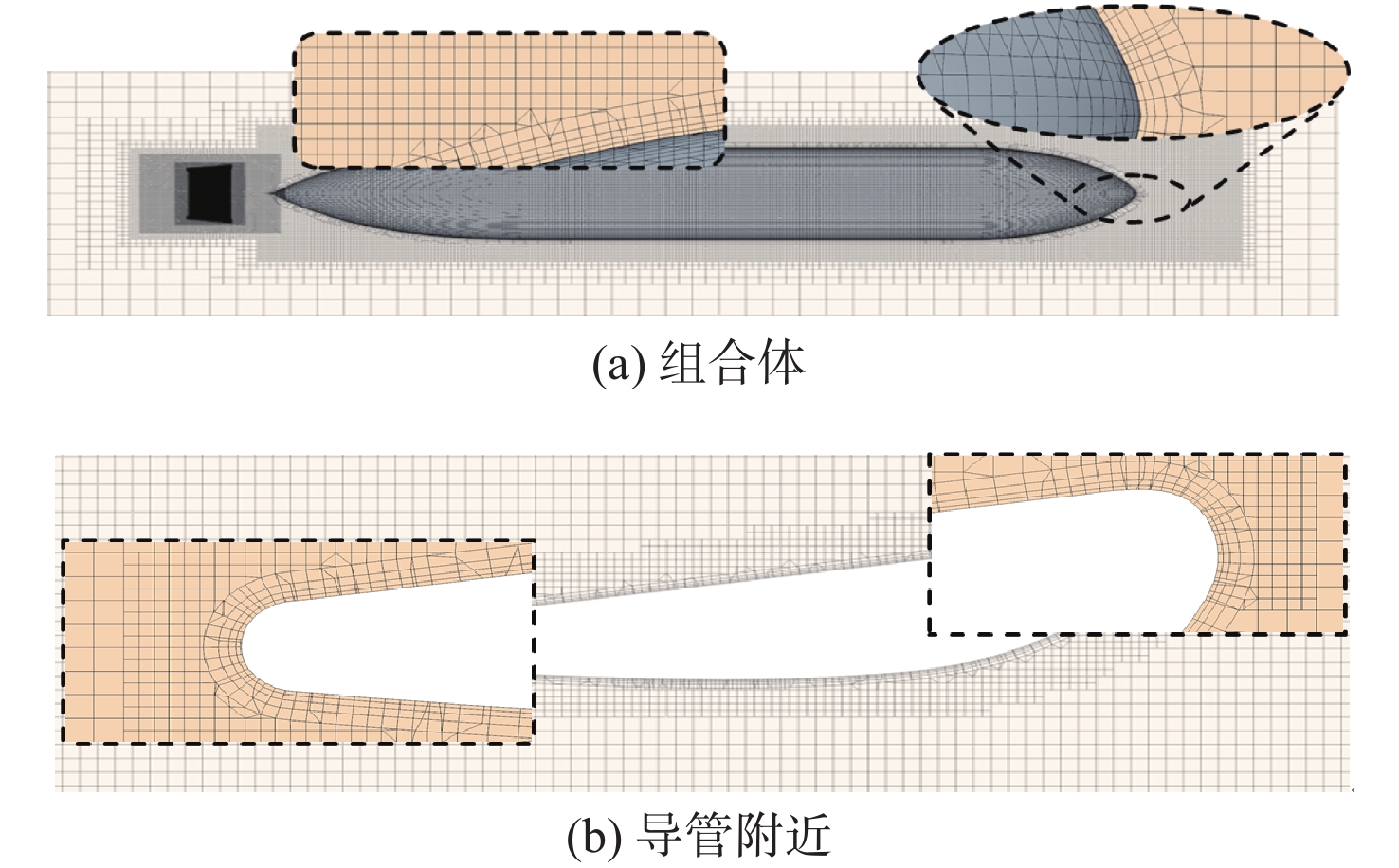
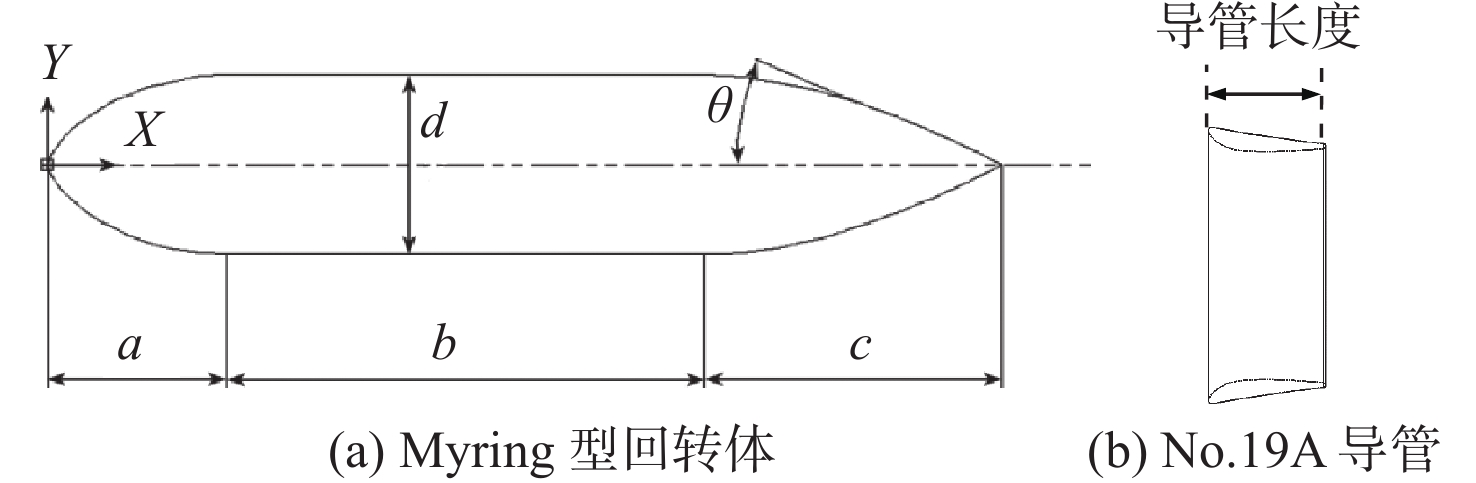
本文选取Myring型回转体和荷兰船模试验水池著名的No.19A导管作为研究对象。Myring型回转体和No.19A导管的几何外形图如图1所示。表1给出了回转体和导管（组合体）的主要参数。
表 1 导管螺旋桨和回转体的主要参数Table 1. Main parameters of ducted propeller and revolution body参数 数值 参数 数值 螺旋桨直径D/mm 47.30 回转体直径d/mm 94.60 螺距比P/D 1 回转体首部长a/mm 94.60 毂径比 0.18 回转体平行中体长b/mm 252.26 桨叶数 4 回转体尾部长c/mm 157.16 导管长度/mm 23.65 回转体尾部离去角θ/(°) 40 计算域及边界条件如图2所示。流体计算域为长方体和组合体之间的区域，长方体的长、宽、高分别为80b，16b和16b。回转体和导管表面为无滑移壁面，长方体除下游边界面为压力出口外，其余5个面均为速度入口。组合体首部距上游边界面24b，距下游边界面55b，距左右边界面皆约8b。图3所示为组合体的网格划分及加密图。对回转体及导管周围网格进行加密以准确捕捉变化梯度大的物理量。近壁处最外层的贴体网格尺寸应与相邻网格尺寸相当，以使网格过渡自然。回转体设置5层边界层网格，第1层网格高0.5 mm；导管设置4层边界层网格，第1层网格高0.04 mm。对施加了体积力源项的导管内螺旋桨盘面附近区域进行加密，以提高体积力源项分布精度。在导管及回转体壁面设置边界层网格，以使其y+值整体处于60附近。
2. 传统螺旋桨体积力法原理与失真分析
2.1 传统螺旋桨体积力法原理
传统的螺旋桨体积力法是指目前使用最普遍的以Goldstein最佳分布为分布模型的描述型体积力法，亦即经典的H-O模型[7]，本文称“Goldstein分布”方法。
该体积力沿圆柱形虚拟盘轴向均匀分布，径向分布遵循Goldstein最优化分布：
fbx=Axr∗√1−r∗ (4) fbθ=Aθ⋅r∗√1−r∗r∗(1−r′h)+r′h (5) 其中：
Ax=1058⋅TπΔ(3RH+4RP)(RP−RH) Aθ=1058⋅QπΔRP(3RH+4RP)(RP−RH) (6) r∗=r′−r′h1−r′h，r′h=RHRP，r′=rRP 以上式中：fbx，fbθ分别为体积力的轴向分量与切向分量；r为径向坐标；RH为桨毂半径；RP梢圆半径；Δ为虚拟盘厚度；T，Q分别为螺旋桨的推力和扭矩。
2.2 敞水性能模拟失真分析
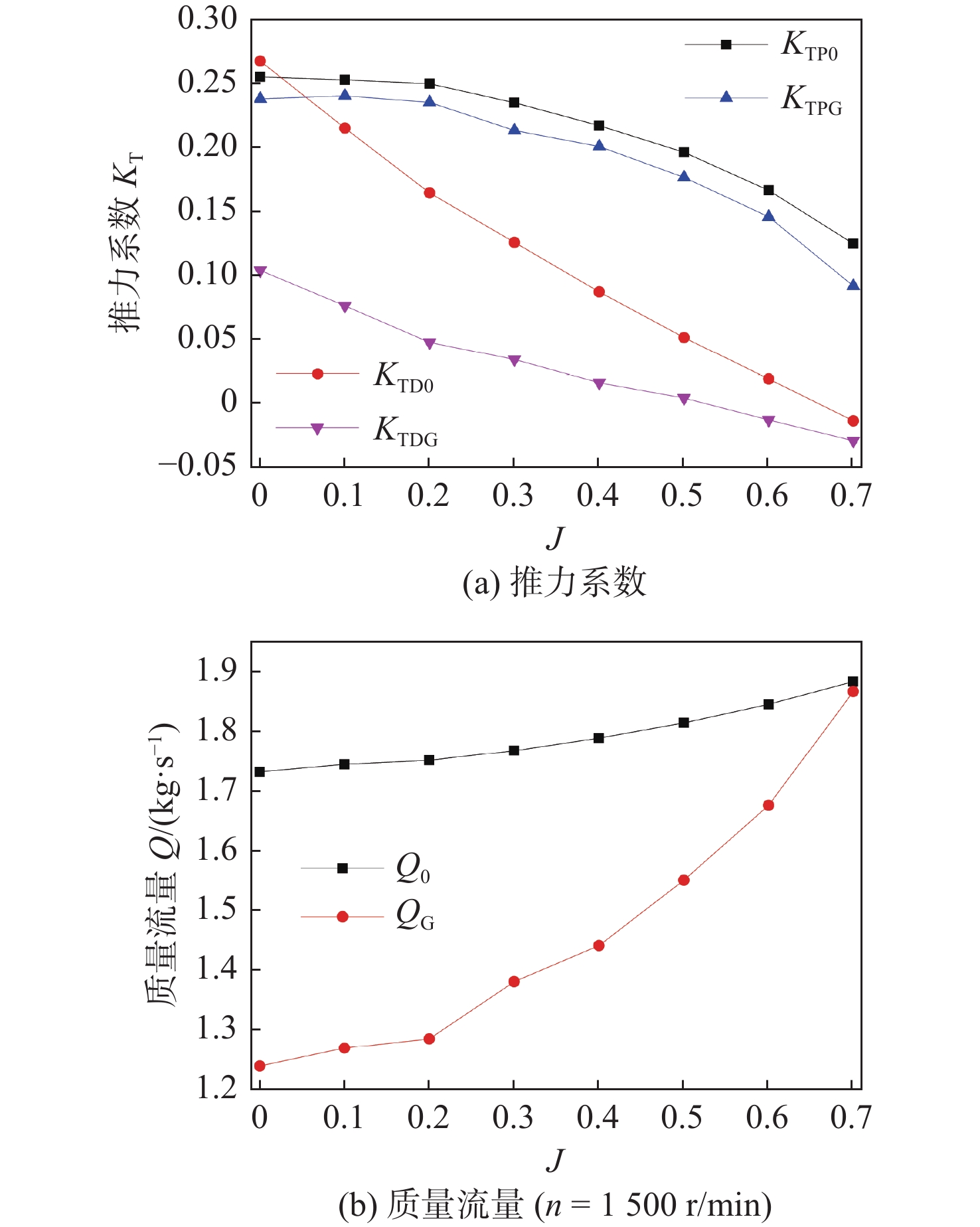
对No.19A导管搭配Goldstein分布型螺旋桨的体积力模型（以下简称“导管+G”）进行数值模拟，探究该模型对导管螺旋桨敞水性能的数值模拟精度以及适用性。仿真场景如图4所示，体积力源分布于导管内部以模拟实体螺旋桨的水动力效应。仿真中，敞水性能曲线取Ka4-70单桨敞水曲线值，进速系数J取导管螺旋桨设计区间0.1～0.7，螺旋桨体积力模型转速n恒为1 500 r/min。导管+G的敞水性能曲线仿真结果如图5（a）所示。图中，KTPG和KTDG分别为桨推力系数及导管推力系数，KTP0和KTD0为相应的试验值[17]。
![]()
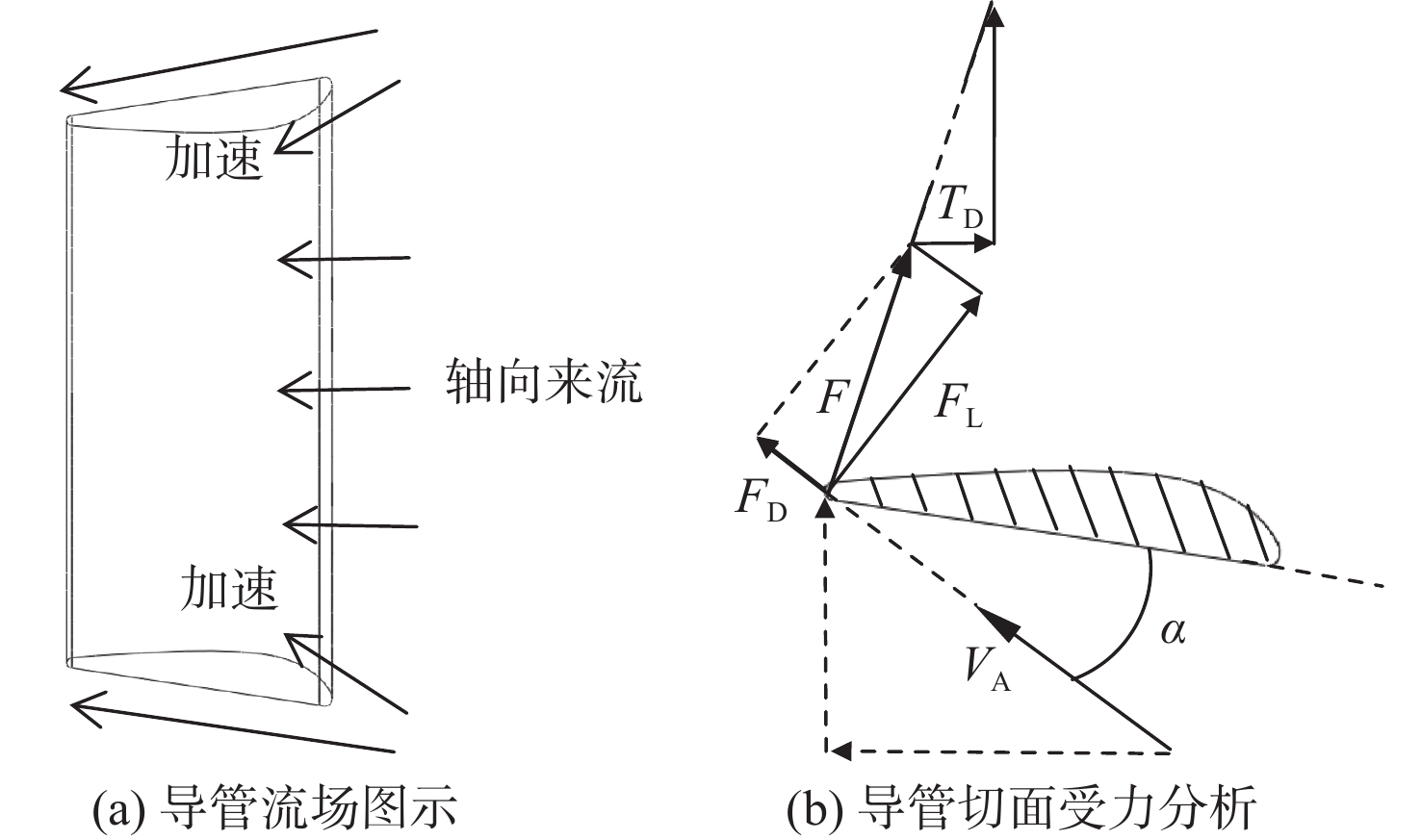
图 5 No.19A导管搭配Goldstein分布的敞水性能曲线Figure 5. Open water performance curves of No.19A ducted propeller with Goldstein distribution由图5（a）可见，桨推力系数与试验值的变化趋势一致，平均相对误差为−8%；而导管推力系数与试验值的变化趋势则相去甚远，平均相对误差在50%以上。为了探究导管推力仿真值精度较低的原因，对导管的受力进行了分析。导管流场和导管切面的受力分析如图6所示。图中，FL和FD分别为翼型升力与阻力，F为合力。No.19A导管属加速型导管，可使流入桨盘的水流加速，从而形成导管内部流速相对较高、导管外部流速相对较低的流场特征。在导管和螺旋桨的共同作用下，导管切面的来流速度VA如图6（b）所示。导管切面可以视为翼型，α为攻角，当导管内、外的轴向流速比增大时，攻角增大，反之减小。当攻角α较大时，合力F的轴向分力TD指向上游，此时，导管产生前进方向的推力TD；当攻角恰好为使得合力F的方向为径向的某值时，导管推力TD= 0；同理，当攻角较小时，导管将产生指向下游的负推力。因此，导管推力与导管和螺旋桨耦合的水动力有关，然而Goldstein分布型螺旋桨体积力模型却并未考虑导管和螺旋桨的相互作用，导致导管推力系数的模拟值与试验值之间差异较大。
攻角的大小（或导管内外轴向流速比）影响翼型的升阻比，亦即影响导管推力TD的大小。导管内部流体的质量流量是导管内外轴向流速比的宏观表征。各进速系数下的导管螺旋桨内流量QG如图5（b）所示，其中Q0为No.19A+Ka4-70实体导管螺旋桨的数值仿真结果。由图可见，QG远小于Q0，差异较大。该差异是随进速系数J的增大而减小的，这同导管推力系数与试验值间差异的变化趋势相同，即进速系数越大，质量流量间的差异越小，导管推力系数的相对误差也就越小。该现象与上述关于导管推力仿真值精度较低原因的分析相符。质量流量间的差异现象或与转子的阻塞效应有关。
3. 改进螺旋桨体积力方法
针对上节中提到的Goldstein分布型螺旋桨体积力模型未考虑导管和螺旋桨的相互作用而使得推力模拟不准确的问题，本文将从质量流量和体积力分布这2个方面提出修正措施，以改进传统螺旋桨体积力方法。
3.1 质量流量修正
为实现质量流量修正，本文在计算螺旋桨进速系数时以校正进速系数J∗替代常规进速系数J。校正进速系数J∗的表达式如下：
J∗=V∗AnD=VInflowPlane−λVinducednD (7) 即在诱导速度Vinduced前引入流量修正系数λ，此时，校正进速为入流面速度VInflowPlane减去λ倍诱导速度λVinduced。当λ≡0时，表示是未经质量流量修正的常规进速系数J。此处进行两点简化处理：一是仅考虑轴向诱导速度；二是诱导速度同时包含螺旋桨和导管所诱导的速度。质量流量Q的定义为
Q=ρSVInflowPlane (8) 式中，S为入流面（过流断面）面积。
根据式（7）、式（8）关于校正进速系数J*和质量流量Q的定义可知，若螺旋桨转速和远处的来流速度（航速）不变，根据动量定理，当加速型导管螺旋桨（体积力）正转时，螺旋桨盘面轴向速度增量|ΔVInflow|小于导管出口处的轴向速度增量|ΔVinduced|。易知当λ>1时，入流面（桨盘面）进速因λ的存在而产生的变化量|ΔVInflow|总是小于诱导速度因λ的存在而产生的变化量|ΔλVinduced|。故当λ>1时，校正进速V∗A减小，即J*值减小，此时桨推力系数增大，体积力源项增大，从而入流面流速VInflowPlane增大，质量流量Q增大（导管推力系数增大）。由图5可见，这也正是本文想要达到的修正效果。
流量修正系数λ可按如下流程求解：
1） 通过数值模拟，获取某转速下实体导管螺旋桨航速V和Q0的数值关系Q0=f(V)；
2） 通过数值模拟，获取导管+体积力模型的λ，V与质量流量Q的数值关系λ=g(V,Q)；
3） 由数值求解获取的实时航速v插值求得Q0，再代入λ=g(v,Q0)，插值求得λ=g(v,f(v))。
修正后的螺旋桨改进体积力法实现流程如图7所示。为凸显该流程与传统体积力法流程的不同之处，特将修改或新增的步骤以虚线框画出。
![]()
图 7 Goldstein分布法和改进体积力法流程图Figure 7. Flow chart of the Goldstein distribution method and improved body force method3.2 体积力分布修正
对导管水动力性能影响较大的是导管壁面周围的流速分布。在质量流量总体相等的情况下，不同形式的体积力分布仍能通过改变导管周围的流速来影响导管推力TD的大小，故而有必要选择适当的体积力分布。
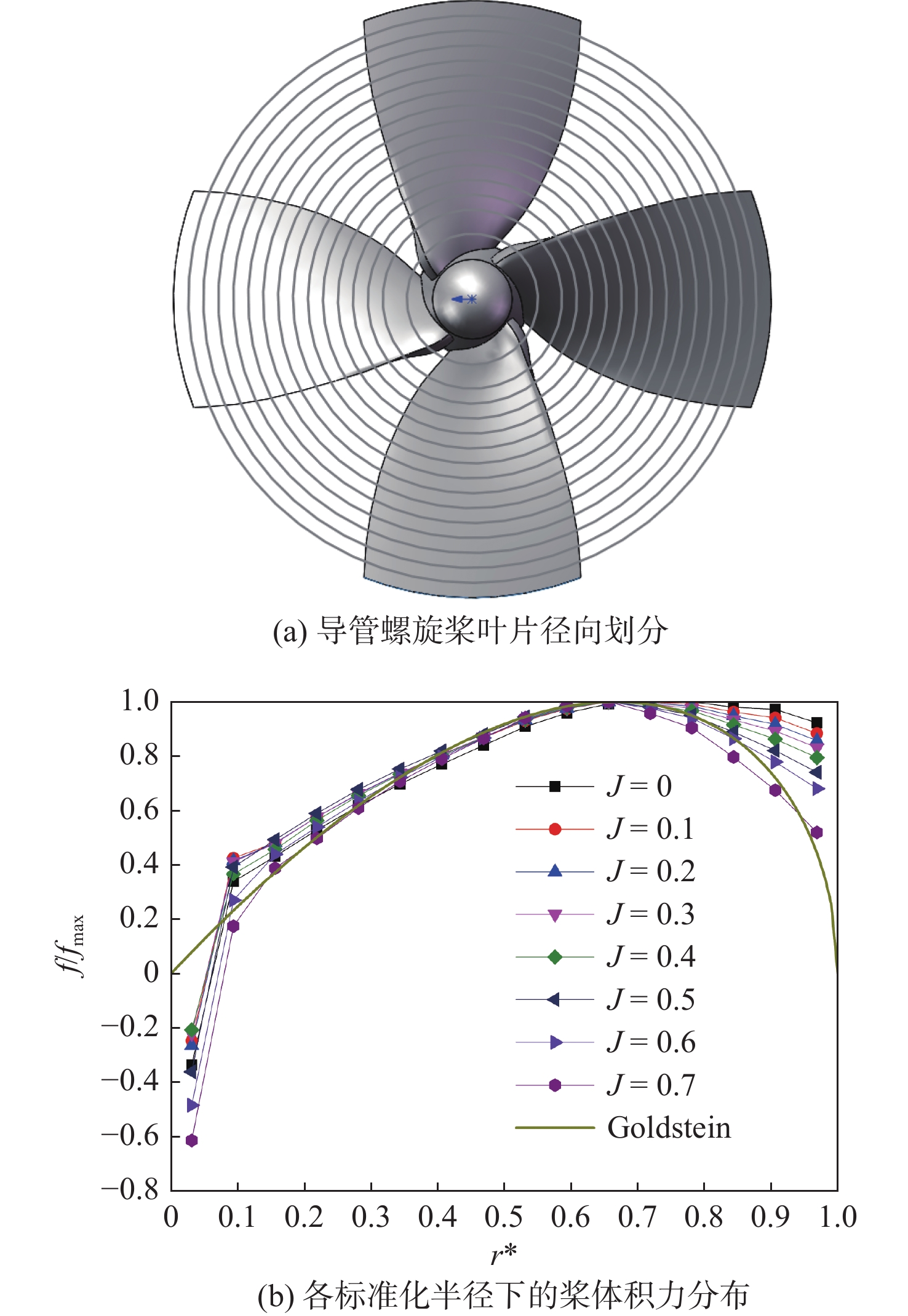
现通过数值模拟获得各进速系数下No.19A+Ka4-70实体导管螺旋桨推力沿标准化半径r∗的分布，再经各半径处体积加权后得到桨推力对应的体积力分布，最后将其与Goldstein最佳分布相比较。标准化半径r∗可以表示为
r∗=r−RHRP−RH (9) 螺旋桨径向划分形式及各标准化半径下的桨体积力分布如图8所示。图中，体积力f以其最大值fmax进行了归一化处理。当 {r^*} \leqslant {\text{0}}{\text{.65}} 时，实体导管螺旋桨体积力的分布曲线与Goldstein最佳分布近似；当 {r^*} \geqslant {\text{0}}{\text{.65}} 时，实体导管螺旋桨归一化的体积力值递减，进速系数J越大，衰减越快，但基本大于0.6，而Goldstein最佳分布的体积力在 {r^*} \geqslant {\text{0}}{\text{.8}} 时小于模拟值，且在 {r^*} = {\text{1}} 处（叶梢）为0。实体导管螺旋桨体积力分布和Goldstein最佳分布间特征迥异，得出的结果与文献[8]相符。
![]()
图 8 导管螺旋桨径向划分形式及各标准化半径下的桨体积力分布Figure 8. Radial division form and the body force distribution under each standardized radius of ducted propeller根据归一化桨体积力分布的特点，本文探究了2种体积力分布形式在导管螺旋桨水动力性能模拟中的适用性。
1） 简单均布。
\frac{f}{{{f_{\max }}}} = {\text{1}} (10) 2） 由于各进速系数J下归一化桨体积力值的变化趋势近似，择其一（本文取J = 0.4时的体积力分布）替代Goldstein最佳分布进行体积力分布修正。经曲线拟合，该修正体积力分布的表达式如下：
\frac{f}{{{f_{\max }}}} = \sum\limits_{i = {\text{0}}}^6 {{a_i}{{({r^*})}^i}} (11) 式中，ai为系数，其取值分别为 {a_{\text{0}}} = 0.541 9， {a_{\text{1}}} = 16.443， {a_{\text{2}}} = −50.745， {a_{\text{3}}} = 129.8， {a_{\text{4}}} = −168.74， {a_{\text{5}}} = 91.85， {a_{\text{6}}} = −15.435。
4. 计算方法验证
4.1 实体导管螺旋桨敞水推力验证
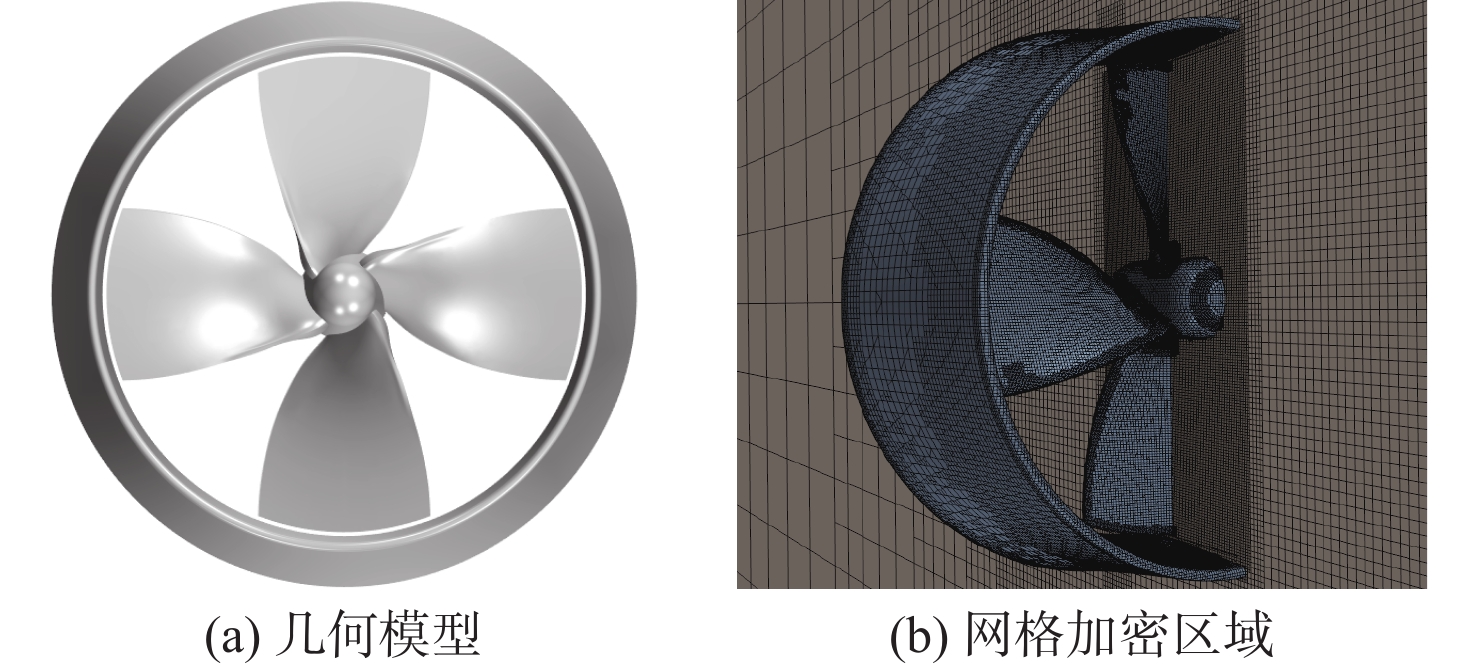
对No.19A+Ka4-70(P/D = 1)导管螺旋桨进行数值模拟，并将导管推力、螺旋桨推力等的仿真结果与试验值进行对比以验证计算方法的合理性。导管螺旋桨的几何模型和网格加密区域如图9所示。计算域由包含导管的计算域和包含螺旋桨的圆柱体计算域组成。圆柱体轴线与桨轴线重合，其侧面及2个底面是前述2个计算域内部的交界面。对螺旋桨与导管的间隙、导边随边及桨叶附近区域进行加密以捕捉变化剧烈的物理量。通过调整导管螺旋桨壁面及其附近网格，得到3套网格。采用多重参考系技术模拟螺旋桨的转动效应。推力模拟结果及其与试验值的对比如表2所示。由表可见，随着网格数量的增大，螺旋桨推力系数{K_{{\text{TP}}}}和导管推力系数{K_{{\text{TD}}}}的相对误差整体上呈递减趋势。 {K_{{\text{TD}}}} 的仿真绝对值与试验值较为一致，而相对误差略大，这是因为导管推力系数绝对值较小，对误差较为敏感； {K_{{\text{TP}}}} 的相对误差小于5%，在误差允许范围内。兼顾计算成本与精度，后文的导管螺旋桨皆采用网格2的相关设置。
![]()
图 9 No.19A+Ka4-70 (P/D = 1)导管螺旋桨几何模型及网格图示Figure 9. Geometric model and mesh refinement of No.19A+Ka4-70 (P/D = 1) ducted propeller表 2 导管螺旋桨推力计算方法验证Table 2. Verification of thrust calculation method for the ducted propeller进速系数J 推力系数仿真值 试验值 相对误差/% 网格1（109万） 网格2（160万） 网格3（194万） 网格1 网格2 网格3 螺旋桨推力系数 0.1 0.247 6 0.252 6 0.253 2 0.252 4 −1.892 0.053 0.287 0.3 0.224 5 0.229 5 0.230 1 0.234 6 −4.301 −2.196 −1.940 0.6 0.153 7 0.161 2 0.162 1 0.166 3 −7.591 −3.089 −2.548 导管推力系数 0.1 0.189 8 0.202 9 0.2029 0.214 8 −11.610 −5.550 −5.543 0.3 0.100 1 0.110 6 0.111 3 0.125 7 −20.340 −12.040 −11.480 0.6 0.009 3 0.017 4 0.017 5 0.018 8 −50.520 −7.549 −7.123 4.2 回转体阻力验证
为了研究回转体与导管螺旋桨耦合下的整体水动力性能，需要对回转体的水动力模拟方法予以验证。对文献[18]中具有试验数据的“组合1”型Myring回转体进行数值仿真，通过加密回转体壁面及其附近网格，得到3了套网格，通过将模拟结果及其与试验值的对比，得到如表3所示结果。由表3可知，回转体在各航速下的阻力模拟值与试验值吻合较好，随着网格数的增加，相对误差逐渐降低。其中，网格b最大的相对误差为−7.727%，仿真结果在误差允许范围内且与网格c相近。因此，为了兼顾计算成本与精度，后文皆采用网格b的相关设置。
表 3 回转体阻力计算方法验证Table 3. Verification of calculation method resistance for the revolution body来流速度/kn 回转体阻力仿真值/N 试验值/N 相对误差/% 网格a（45万） 网格b（107万） 网格c（143万） 网格a 网格b 网格c 0.3 0.355 5 0.372 9 0.373 2 0.379 1 −6.237 −1.648 −1.569 0.5 0.877 8 0.909 2 0.909 5 0.940 0 −6.617 −3.276 −3.244 0.7 1.605 0 1.644 0 1.646 0 1.706 0 −5.903 −3.593 −3.476 0.9 2.528 0 2.574 0 2.577 0 2.790 0 −9.362 −7.727 −7.616 5. 计算结果与分析
5.1 基于改进体积力法的导管螺旋桨敞水水动力性能
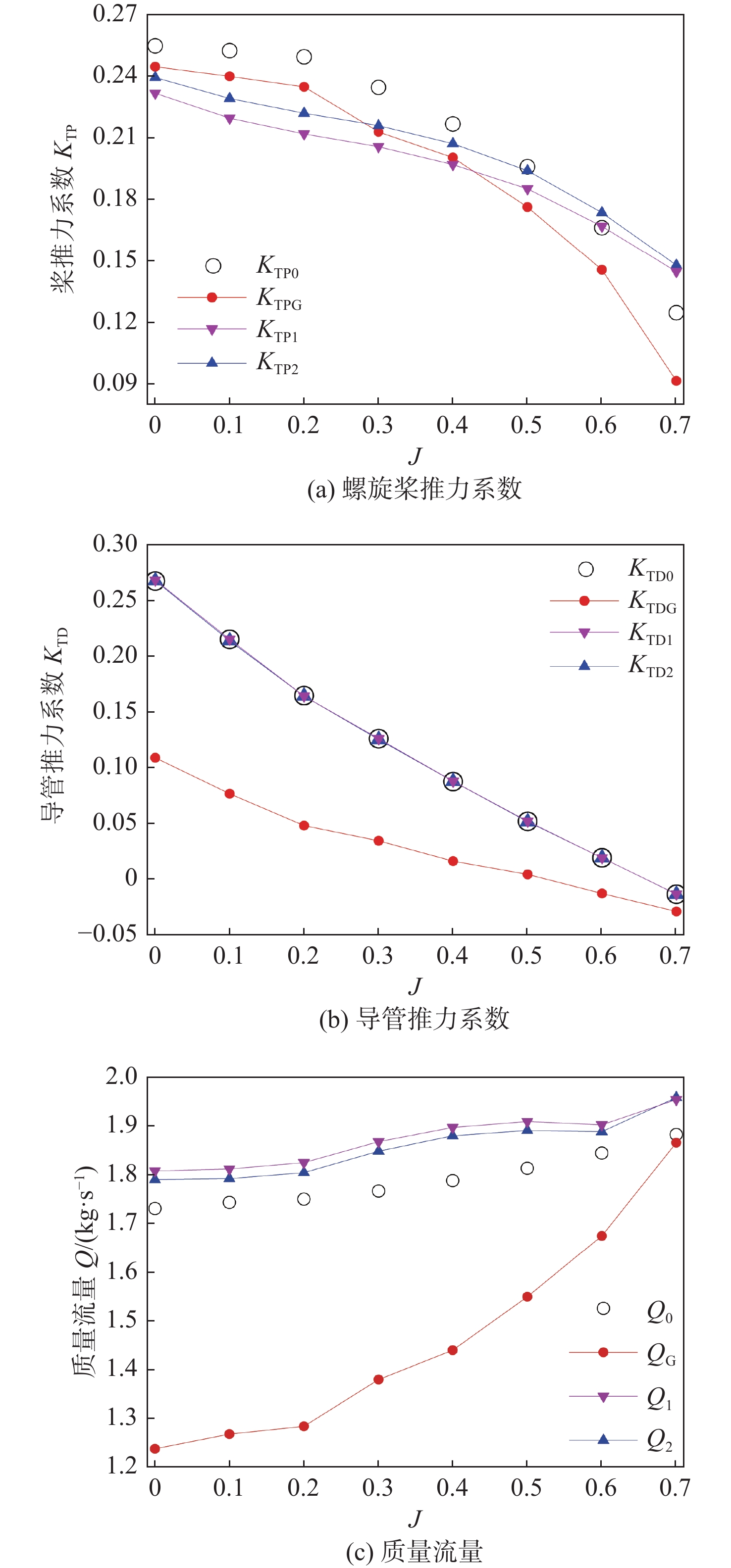
使用经流量修正和分布修正的改进螺旋桨体积力模型对No.19A+Ka4-70导管螺旋桨进行敞水水动力性能数值模拟。螺旋桨推力系数 {K_{{\text{TP}}}} 、导管推力系数{K_{{\text{TD}}}}和质量流量Q如图10所示，图中参数的下标0，G，1，2分别代表试验值[17]、Goldstein最佳分布、由式（10）定义的分布（均布，简称“分布1”）和由式（11）定义的分布（简称“分布2”）。为叙述方便，下文将经流量修正的均布形式的改进体积力法称为改进体积力法1，将经流量修正的分布2形式的改进体积力法称为改进体积力法2。
![]()
图 10 基于改进体积力法的导管螺旋桨敞水性能曲线对比Figure 10. Comparison of open water performance curves of the ducted propeller based on improved body force method总览图10，发现基于改进体积力法1和改进体积力法2所得导管螺旋桨的各参数皆与试验值吻合较好。其中，改进体积力法1和改进体积力法2的桨推力系数 {K_{{\text{TP}}}} 的平均相对误差分别为7.8%和10%，略优于Goldstein分布方法（其 {K_{{\text{TP}}}} 的平均相对误差为10%）；导管推力系数 {K_{{\text{TD}}}} 的相对误差约为0.1%，说明2个改进模型均能较好地解决导管水动力模拟不准确的问题。改进体积力法1和改进体积力法2的质量流量Q的变化趋势与试验值相同，其平均相对误差分别为4.5%和3.7%，在工程可接受范围内。而Goldstein分布方法的 {K_{{\text{TD}}}} 和Q的平均相对误差绝对值分别为90.3%和18.5%，已完全失真，且导管螺旋桨常用的重载工况（低进速系数J）误差高于轻载工况。表4中，总推力系数 {K_{{\text{TT}}}} 为 {K_{{\text{TP}}}} 与 {K_{{\text{TD}}}} 之和。基于Goldstein分布方法，各进速系数下的 {K_{{\text{TT}}}} 较试验值约小30%，误差较大，而两种改进方法间的误差则仅约5%。其中J = 0.7因在设计进速系数以外，使得 {K_{{\text{TT}}}} 的误差较大，故计算相对误差均值时不予考虑。
表 4 敞水工况下导管螺旋桨的总推力系数Table 4. Total thrust coefficients of the ducted propeller in open water condition进速系数J 总推力系数KTT 试验值 相对误差/% Goldstein分布方法 改进体积力法1 改进体积力法2 Goldstein分布法 改进体积力法1 改进体积力法2 0 0.353 4 0.499 8 0.506 9 0.521 9 −32.28 −4.24 −2.87 0.1 0.316 3 0.434 6 0.442 8 0.467 3 −32.29 −7.00 −5.24 0.2 0.282 6 0.376 0 0.386 0 0.413 8 −31.70 −9.14 −6.71 0.3 0.247 1 0.331 5 0.341 1 0.360 3 −31.42 −7.99 −5.34 0.4 0.216 3 0.284 6 0.294 7 0.303 9 −28.81 −6.36 −3.04 0.5 0.180 4 0.236 9 0.245 3 0.247 5 −27.09 −4.29 −0.86 0.6 0.132 6 0.185 9 0.192 5 0.185 1 −28.37 0.40 4.01 0.7 0.062 3 0.131 0 0.134 1 0.110 8 −43.80 18.20 20.94 |平均值| 30.20 5.60 4.00 基于改进体积力法的导管螺旋桨的流速分布如图11所示。根据体积力分布形式的不同，分布1（均布）下的流速沿径向分布较均匀，而分布2下的流速则随径向距离的增大而增大。两种体积力分布形式下的导管推力系数 {K_{{\text{TD}}}} 几乎相同，而桨推力系数 {K_{{\text{TP}}}} 则有所差异，这是因为分布1和分布2对决定导管推力的导管近流场影响较小，而对桨（入流面）所在区域的流场影响较大。改进体积力法1对 {K_{{\text{TP}}}} 的模拟较改进体积力法2更准确，但两者的 {K_{{\text{TP}}}} 偏小与螺旋桨体积力法本身将某选定入流平面的平均速度取作进速的简易处理有关。总之，改进体积力法整体上可以较好地实现对敞水导管螺旋桨水动力数值的模拟，优于传统螺旋桨体积力法，可为准确模拟艇体−导管桨（体积力）耦合水动力奠定基础。
![]()
图 11 基于改进体积力法的敞水导管螺旋桨的流速分布图（J = 0.3）Figure 11. Flow velocity distribution of the ducted propeller in open water based on improved body force method (J = 0.3)5.2 基于改进体积力法的艇−导管螺旋桨耦合水动力性能
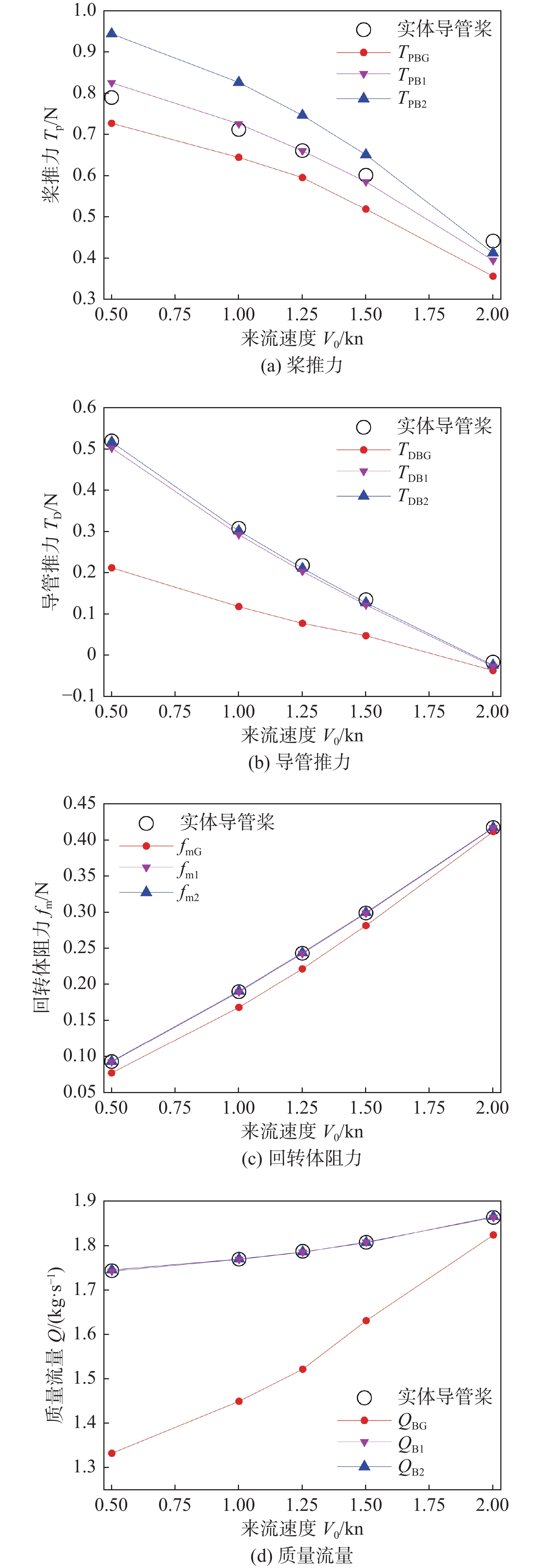
导管螺旋桨体积力模型的提出最终是为了提高搭配导管螺旋桨的航行器数值模拟的精度和效率，故本节将导管螺旋桨体积力模型与实体导管螺旋桨模型搭配回转体后的仿真值进行了对比，以进一步研究艇后改进体积力法1和改进体积力法2的适用性。模拟时，组合体保持静止，螺旋桨转速恒定为1 500 r/min，通过改变来流速度计算不同工况下的水动力性能。桨推力 {T_{\text{P}}} 、导管推力 {T_{\text{D}}} 、回转体阻力 {f_{\text{m}}} 和质量流量Q的性能曲线如图12所示。图中：实体导管桨表示实体导管螺旋桨模型搭配回转体的工况；下标B表示艇后工况，以区别于敞水工况；下标1，2，G分别表示改进体积力法1、改进体积力法2和Goldstein分布方法。
![]()
图 12 基于改进体积力法的回转体后导管螺旋桨的性能曲线对比Figure 12. Performance curves of the ducted propeller behind revolution body based on improved body force method由图12可见，相较艇后实体导管螺旋桨工况，基于Goldstein分布方法、改进体积力法1和改进体积力法2的桨推力 {T_{\text{P}}} 的平均相对误差分别为−12%，1.3%和14.0%；基于改进体积力法1和改进体积力法2的导管推力 {T_{\text{D}}} 、质量流量Q，尤其是回转体阻力fm，皆与艇后实体导管螺旋桨相应的仿真值吻合较好，相对误差仅约0.5%，与Goldstein分布方法相比精度提升较大。质量流量模拟的准确性不仅影响着导管推力，还影响着回转体尾部压力场（回转体阻力）。采用改进体积力法准确预报艇体−导管螺旋桨的耦合水动力可为模拟水下航行器的操纵性动态打下基础。另外，由图12（b）～图12（d）可见，随着来流速度逐渐增大，基于Goldstein分布方法的导管推力 {T_{\text{D}}} 、回转体阻力fm和质量流量Q与实体螺旋桨模型间的误差逐渐减小。这是因为当进速增大时，螺旋桨水动力螺距角减小，由体积力源所模拟的桨叶升力这一水动力效应减弱，进而导致桨−导管耦合水动力效应减弱，从而使得因模拟耦合效应失真而产生的误差也随之减小。
由表5可见，在各来流速度（不含2 kn）下，改进体积力法1和改进体积力法2的前进合力的平均相对误差绝对值分别为1.86%和11.65%，较Goldstein分布方法的平均相对误差绝对值（30.28%）大幅降低。与敞水工况相似，改进体积力法1于艇后仍有较高的精度，优于方法2。总而言之，改进体积力法整体上较好地实现了对艇后导管螺旋桨水动力数值的模拟，其计算精度均较Goldstein分布方法有较大的提升，也优于传统螺旋桨体积力法，适用于艇体−导管−体积力耦合水动力的数值模拟。
表 5 艇后工况艇−桨前进合力Table 5. Resultant force of the ducted propeller and the revolution body来流速度/kn 前进合力/N 实体模型仿真值/N 相对误差/% Goldstein分布方法 改进法1 改进法2 Goldstein分布方法 改进体积力法1 改进体积力法2 0.50 0.863 8 1.237 1 1.370 4 1.219 0 −29.13 1.48 12.42 1.00 0.595 9 0.830 9 0.939 7 0.831 7 −28.35 −0.10 12.97 1.25 0.453 1 0.622 6 0.714 9 0.637 5 −28.92 −2.33 12.13 1.50 0.286 5 0.410 4 0.478 8 0.439 0 −34.73 −6.50 9.08 2.00 −0.090 5 −0.047 3 −0.029 3 0.008 6 −1 152.30 −650.00 −440.70 |平均值| 30.28 1.86 11.65 上节提到，在敞水工况下，当进速系数较大（ J \geqslant 0.7 ）时，采用体积力法模拟导管螺旋桨推力误差较大（表4），从图12（a）、图12（b）和表5可以看出，在艇后工况下，高来流速度（2 kn）时亦如此。现将就该问题予以探讨。在高进速系数（进速系数大于导管推力变为阻力时对应的进速系数）下，螺旋桨升力会减少，桨−导管之间的“动水动力效应”随之降低。为便于理解，假设此时螺旋桨停止转动，静止于导管内，承受着高速来流的冲击。体积力法以体积力源代替桨叶，模拟的是螺旋桨的升力效应，而高进速时，桨叶充当的更多的是阻力的角色，桨−导管之间更多地体现为“静水动力效应”。现行的体积力法暂无法模拟桨的阻塞效应，为此，郁程等[10]针对体积力法中桨叶的阻塞效应进行了修正研究。再者，当进速增大时，需要捕捉导管涡脱落等流动现象以精确评估导管的水动力特性，这相当于对大攻角水翼的仿真，而本文所用RANS方法难以胜任。
但是，导管螺旋桨一般被设计用于重载工况（低进速系数），在重载工况下，推力较大、效率较高。在高进速系数下，导管的流动分离严重、效率较低、推力由正转负（形成阻力）。因此相对来说，对重载工况的模拟是导管螺旋桨水动力性能研究的焦点，也是本文的焦点。
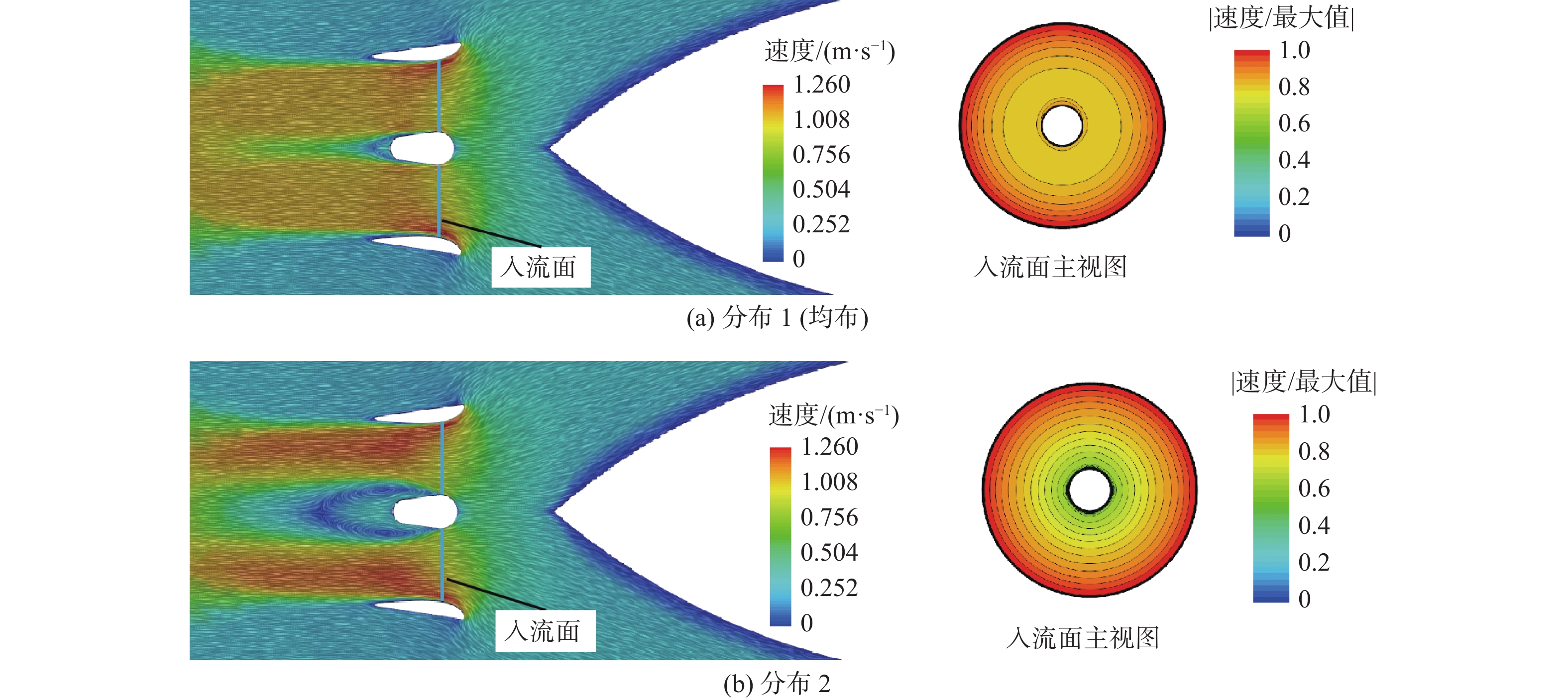
在艇后工况下，基于改进体积力法2的桨推力（或前进合力）相比基于改进体积力法1的桨推力（或前进合力），其偏离实体模型仿真值更多，这与本文对入流面进速的简化处理有关。基于改进体积力法的艇后导管螺旋桨的速度分布如图13所示，其中左图标出了所取入流面的轴向位置，右图为入流面无量纲轴向速度分布（经速度最大值无量纲化）。由图可见，基于改进体积力法1（图13（a））的导管内速度等值线较为疏松，分布相对均匀；而基于改进体积力法2（图13（b））的导管内速度等值线密集，分布较不均匀。本文取入流面整体的轴向平均速度为螺旋桨进速，因忽略了来流空间不均匀性对导管螺旋桨水动力性能的影响，使得体积力源无法基于当地进速进行分布。在后续的研究中，可取各半径处的局部速度为进速以分布体积力源，并将外界来流速度的分布考虑在内。而均布式体积力因改善了来流分布的不均匀性，取得了较高的模拟精度，可作为入流面进速简易处理法的补偿方式。
![]()
图 13 基于改进体积力法的艇−导管螺旋桨速度分布图（来流速度为0.5 kn）Figure 13. Flow velocity distribution of the ducted propeller behind ship based on improved body force method (incoming flow velocity is 0.5 kn)6. 结 语
本文基于RANS方法，以No.19A+Ka4-70导管螺旋桨和Myring型回转体模型为研究对象，对Goldstein分布方法在导管螺旋桨水动力性能模拟中的适用性进行了探究。基于机翼理论，分析了导管水动力模拟失真的原因，并以质量流量和体积力分布模型为切入点，提出了修正理论及方法，最后在敞水和艇后这2种工况下对改进螺旋桨体积力模型进行了数值验证。主要得到如下结论：
1） 采用Goldstein分布方法模拟例如导管螺旋桨等的内部流动时，精度较低，水动力数值计算结果不可靠，而本文提出的基于质量流量相等原则的改进体积力法，即引入质量流量修正系数修正导管搭配体积力模型的质量流量，可以使导管搭配体积力的模型与实体导管螺旋桨导管内流场的宏观特征相同（单位时间内通过导管的流体质量相等），得到了适用于导管螺旋桨的高效而准确的改进体积力法。
2） 对于本文所提的适用于导管螺旋桨的改进体积力法，均布式体积力源分布（改进体积力法1）无论是在敞水工况还是在艇后工况中，模拟精度均较高。
3） 改进的螺旋桨体积力法因引入了流量修正，能较好地模拟桨（体积力源）−艇的相互作用，获得了与桨（实体）−艇模型精度相当的艇体阻力和导管桨推力，其精度较Goldstein分布方法有较大的提升。
4） 改进的螺旋桨体积力法虽能得到更准确的导管螺旋桨总推力，但较Goldstein分布方法需要更多关于导管桨本身的信息，例如航速和导管内质量流量的关系。然而，该代价在模拟搭配实体导管螺旋桨的航行器的动态操纵性所需高时耗面前微不足道。
-
![]()
图 5 No.19A导管搭配Goldstein分布的敞水性能曲线
Figure 5. Open water performance curves of No.19A ducted propeller with Goldstein distribution
![]()
图 7 Goldstein分布法和改进体积力法流程图
Figure 7. Flow chart of the Goldstein distribution method and improved body force method
![]()
图 8 导管螺旋桨径向划分形式及各标准化半径下的桨体积力分布
Figure 8. Radial division form and the body force distribution under each standardized radius of ducted propeller
![]()
图 9 No.19A+Ka4-70 (P/D = 1)导管螺旋桨几何模型及网格图示
Figure 9. Geometric model and mesh refinement of No.19A+Ka4-70 (P/D = 1) ducted propeller
![]()
图 10 基于改进体积力法的导管螺旋桨敞水性能曲线对比
Figure 10. Comparison of open water performance curves of the ducted propeller based on improved body force method
![]()
图 11 基于改进体积力法的敞水导管螺旋桨的流速分布图（J = 0.3）
Figure 11. Flow velocity distribution of the ducted propeller in open water based on improved body force method (J = 0.3)
![]()
图 12 基于改进体积力法的回转体后导管螺旋桨的性能曲线对比
Figure 12. Performance curves of the ducted propeller behind revolution body based on improved body force method
![]()
图 13 基于改进体积力法的艇−导管螺旋桨速度分布图（来流速度为0.5 kn）
Figure 13. Flow velocity distribution of the ducted propeller behind ship based on improved body force method (incoming flow velocity is 0.5 kn)
表 1 导管螺旋桨和回转体的主要参数
Table 1 Main parameters of ducted propeller and revolution body
参数 数值 参数 数值 螺旋桨直径D/mm 47.30 回转体直径d/mm 94.60 螺距比P/D 1 回转体首部长a/mm 94.60 毂径比 0.18 回转体平行中体长b/mm 252.26 桨叶数 4 回转体尾部长c/mm 157.16 导管长度/mm 23.65 回转体尾部离去角 \theta /(°) 40 
下载: 导出CSV
表 2 导管螺旋桨推力计算方法验证
Table 2 Verification of thrust calculation method for the ducted propeller
进速系数J 推力系数仿真值 试验值 相对误差/% 网格1（109万） 网格2（160万） 网格3（194万） 网格1 网格2 网格3 螺旋桨推力系数 0.1 0.247 6 0.252 6 0.253 2 0.252 4 −1.892 0.053 0.287 0.3 0.224 5 0.229 5 0.230 1 0.234 6 −4.301 −2.196 −1.940 0.6 0.153 7 0.161 2 0.162 1 0.166 3 −7.591 −3.089 −2.548 导管推力系数 0.1 0.189 8 0.202 9 0.2029 0.214 8 −11.610 −5.550 −5.543 0.3 0.100 1 0.110 6 0.111 3 0.125 7 −20.340 −12.040 −11.480 0.6 0.009 3 0.017 4 0.017 5 0.018 8 −50.520 −7.549 −7.123
下载: 导出CSV
表 3 回转体阻力计算方法验证
Table 3 Verification of calculation method resistance for the revolution body
来流速度/kn 回转体阻力仿真值/N 试验值/N 相对误差/% 网格a（45万） 网格b（107万） 网格c（143万） 网格a 网格b 网格c 0.3 0.355 5 0.372 9 0.373 2 0.379 1 −6.237 −1.648 −1.569 0.5 0.877 8 0.909 2 0.909 5 0.940 0 −6.617 −3.276 −3.244 0.7 1.605 0 1.644 0 1.646 0 1.706 0 −5.903 −3.593 −3.476 0.9 2.528 0 2.574 0 2.577 0 2.790 0 −9.362 −7.727 −7.616
下载: 导出CSV
表 4 敞水工况下导管螺旋桨的总推力系数
Table 4 Total thrust coefficients of the ducted propeller in open water condition
进速系数J 总推力系数KTT 试验值 相对误差/% Goldstein分布方法 改进体积力法1 改进体积力法2 Goldstein分布法 改进体积力法1 改进体积力法2 0 0.353 4 0.499 8 0.506 9 0.521 9 −32.28 −4.24 −2.87 0.1 0.316 3 0.434 6 0.442 8 0.467 3 −32.29 −7.00 −5.24 0.2 0.282 6 0.376 0 0.386 0 0.413 8 −31.70 −9.14 −6.71 0.3 0.247 1 0.331 5 0.341 1 0.360 3 −31.42 −7.99 −5.34 0.4 0.216 3 0.284 6 0.294 7 0.303 9 −28.81 −6.36 −3.04 0.5 0.180 4 0.236 9 0.245 3 0.247 5 −27.09 −4.29 −0.86 0.6 0.132 6 0.185 9 0.192 5 0.185 1 −28.37 0.40 4.01 0.7 0.062 3 0.131 0 0.134 1 0.110 8 −43.80 18.20 20.94 |平均值| 30.20 5.60 4.00
下载: 导出CSV
表 5 艇后工况艇−桨前进合力
Table 5 Resultant force of the ducted propeller and the revolution body
来流速度/kn 前进合力/N 实体模型仿真值/N 相对误差/% Goldstein分布方法 改进法1 改进法2 Goldstein分布方法 改进体积力法1 改进体积力法2 0.50 0.863 8 1.237 1 1.370 4 1.219 0 −29.13 1.48 12.42 1.00 0.595 9 0.830 9 0.939 7 0.831 7 −28.35 −0.10 12.97 1.25 0.453 1 0.622 6 0.714 9 0.637 5 −28.92 −2.33 12.13 1.50 0.286 5 0.410 4 0.478 8 0.439 0 −34.73 −6.50 9.08 2.00 −0.090 5 −0.047 3 −0.029 3 0.008 6 −1 152.30 −650.00 −440.70 |平均值| 30.28 1.86 11.65
下载: 导出CSV
-
[1] HOUGH G R, ORDWAY D E. The generalized actuator disk[R]. Ithaca, NY: Therm Advanced Research Inc, 1964.
[2] 吴召华, 陈作钢, 代燚, 等. 基于体积力法的船舶回转运动水动力数值研究[J]. 中国舰船研究, 2013, 8(4): 12–19. doi: 10.3969/j.issn.1673-3185.2013.04.003 WU Z H, CHEN Z G, DAI Y, et al. Numerical study of hydrodynamic force on ships in turning motion based on a body-force propeller model[J]. Chinese Journal of Ship Research, 2013, 8(4): 12–19 (in Chinese). doi: 10.3969/j.issn.1673-3185.2013.04.003
[3] 黄晨冉. 基于重叠网格的水下潜器操纵运动直接模拟[D]. 武汉: 武汉理工大学, 2018. HUANG C R. Direct simulation of maneuver of the underwater vehicle based on overset grid[D]. Wuhan: Wuhan University of Technology, 2018 (in Chinese).
[4] GAGGERO S, VILLA D, TANI G, et al. Propeller nozzles design using viscous codes and optimization algorithms[C]//VII International Conference on Computational Methods in Marine Engineering - MARINE 2017, 2017.
[5] 何涛, 冯大奎, 张航, 等. 基于改进体积力方法的实尺度船舶回转运动数值仿真[J]. 中国造船, 2020, 61(增刊2): 52-63. HE T, FENG D K, ZHANG H, et al. Numerical simulation of full-scale ship turning motion[J]. Shipbuilding of China, 2020, 61(Supp 2): 52-63 (in Chinese).
[6] 吴浩, 欧勇鹏, 向国. 体积力法在船舶自由直航数值计算中的影响因素研究[J]. 武汉理工大学学报(交通科学与工程版), 2017, 41(2): 273–276. WU H, OU Y P, XIANG G. Research on the influencing factors of body force method in numerical simulation of ship self-propulsion[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2017, 41(2): 273–276 (in Chinese).
[7] GOLDSTEIN S. On the vortex theory of screw propellers[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1929, 123(792): 440–465.
[8] 吴家鸣, 赖宇锋, 李江伟, 等. 导管螺旋桨的推力、进速与诱导速度沿盘面的分布特征[J]. 船舶工程, 2016, 38(12): 23–26, 36. doi: 10.13788/j.cnki.cbgc.2016.12.023 WU J M, LAI Y F, LI J W, et al. Distribution characteristics of thrust, advanced and induced velocity on ducted propeller disk[J]. Ship Engineering, 2016, 38(12): 23–26, 36 (in Chinese). doi: 10.13788/j.cnki.cbgc.2016.12.023
[9] FENG D K, YU J W, RAN HE R, et al. Improved body force propulsion model for ship propeller simulation[J]. Applied Ocean Research, 2020, 104: 102328. doi: 10.1016/j.apor.2020.102328
[10] 郁程, 董小倩, 杨晨俊. 侧推器体积力模型及其应用[J]. 上海交通大学学报, 2018, 52(3): 291–296. doi: 10.16183/j.cnki.jsjtu.2018.03.006 YU C, DONG X Q, YANG C J. A body force model for tunnel thrusters and application[J]. Journal of Shanghai Jiao Tong University, 2018, 52(3): 291–296 (in Chinese). doi: 10.16183/j.cnki.jsjtu.2018.03.006
[11] ESLAMDOOST A, VIKSTRÖM M. A body-force model for waterjet pump simulation[J]. Applied Ocean Research, 2019, 90: 101832. doi: 10.1016/j.apor.2019.05.017
[12] KNIGHT B G, MAKI K J. A semi-empirical multi-degree of freedom body force propeller model[J]. Ocean Engineering, 2019, 178: 270–282. doi: 10.1016/j.oceaneng.2019.02.056
[13] 宋长红, 林永峰, 陈文轩, 等. 基于动量源方法的涵道尾桨CFD分析[J]. 直升机技术, 2009(1): 6–11. doi: 10.3969/j.issn.1673-1220.2009.01.002 SONG C H, LIN Y F, CHEN W X, et al. CFD analysis for the ducted tail rotor based on momentum-source method[J]. Helicopter Technique, 2009(1): 6–11 (in Chinese). doi: 10.3969/j.issn.1673-1220.2009.01.002
[14] 杨立, 冯君, 孙文愈, 等. 大型船舶混合吊舱对转桨与船体相互干扰特性研究[J]. 中国造船, 2019, 60(2): 59–68. doi: 10.3969/j.issn.1000-4882.2019.02.006 YANG L, FENG J, SUN W Y, et al. Research on interaction between hybrid CRP pod and hull of large vessel[J]. Shipbuilding of China, 2019, 60(2): 59–68 (in Chinese). doi: 10.3969/j.issn.1000-4882.2019.02.006
[15] MENTER F R, KUNTZ M, LANGTRY R B. Ten years of industrial experience with the SST turbulence model[C]//Turbulence, Heat and Mass Transfer. Antalya: Begell House, 2003.
[16] WILCOX D C. Formulation of the k-ω turbulence model revised[J]. AIAA Journal, 2008, 46(11): 2823–2838. doi: 10.2514/1.36541
[17] 盛振邦, 刘应中. 船舶原理[M]. 上海: 上海交通大学出版社, 2003: 46-47. SHENG Z B, LIU Y Z. Ship theory[M]. Shanghai: Shanghai Jiao Tong University Press, 2003: 46-47 (in Chinese).
[18] 庞永杰, 王亚兴, 杨卓懿, 等. Myring型回转体直航阻力计算及艇型优化[J]. 哈尔滨工程大学学报, 2014, 35(9): 1093–1098. doi: 10.3969/j.issn.1006-7043.201304028 PANG Y J, WANG Y X, YANG Z Y, et al. Direct route drag calculation and shape optimization of Myring shape axisymmetric revolution body[J]. Journal of Harbin Engineering University, 2014, 35(9): 1093–1098 (in Chinese). doi: 10.3969/j.issn.1006-7043.201304028
-
期刊类型引用(2)
1. 肖海松，潘露峰，史泽宇，郑昊然. 典型推进器在高性能舰船中的应用. 船舶. 2024(03): 43-51 . 
百度学术
2. 陆德顺，孙铁志，张桂勇. 导管螺旋桨水动力特性仿真分析. 船舶. 2023(06): 102-110 . 百度学术
其他类型引用(1)
-
其他相关附件
-
本文双语pdf
ZG2920_en 点击下载(1594KB)
-
计量
- 文章访问数: 642
- HTML全文浏览量: 99
- PDF下载量: 87
- 被引次数: 3
