Numerical investigation on water-entry slamming load of large trimaran cconnecting bridge using OpenFOAM
-
摘要:目的 旨在探究三体船连接桥落体砰击载荷分布规律。方法 基于OpenFOAM开源软件以及连续性方程和N-S方程,建立三体船连接桥自由落体入水砰击数值模型,模拟三体船连接桥自由落体入水砰击过程中的速度、砰击压力以及自由液面动态变化,开展网格收敛性分析,验证数值计算方法的正确性,并将数值解与实验值进行对比。结果 结果显示,所提模型能够有效预报三体船连接桥结构的落体砰击载荷,靠近外折角点的连接桥砰击压力系数最大,得到了连接桥下表面砰击压力峰值及砰击压力系数与速度的关系。结论 研究给出的三体船连接桥入水砰击压力特性和范围可为三体船结构强度评估与结构设计提供数值基础。Abstract:Objective The purpose of this paper is to explores the slamming load distribution of a trimaran connecting bridge.Methods Based on OpenFOAM open source software and starting with the continuity equation and N-S equation, this paper establishes a free entry slamming numerical model of a trimaran connecting bridge. The dynamic changes of velocity, slamming pressure and free surface during the free entry slamming process of the trimaran connecting bridge are simulated. The convergence analysis of the grid is carried out, and the numerical solution is compared with the experimental solution to verify the accuracy of the numerical calculation method.Results The results show that this method can effectively predict the falling body slamming load of a trimaran connecting bridge structure. It is found that the slamming pressure coefficient of the connecting bridge is largest near the outer corner. The peak value of the slamming pressure on the lower surface of the connecting bridge and the relationship between the slamming pressure coefficient and velocity are then obtained.Conclusions This study presents the characteristics and range of slamming pressure on a trimaran connecting bridge, providing a numerical basis for the structural strength evaluation and design of trimarans.
-
0. 引 言
随着科技的进步和能源结构的转变,集装箱船正逐渐演变为海上浮式仓储中心。为追求更好的经济效应,集装箱船的大型化已成为未来发展的必然趋势。然而,随着船体尺度的不断增大,外界波浪载荷引起的非线性现象愈发显著。这种非线性波浪载荷会导致船舶在航行中出现严重的结构疲劳破坏,从而对船舶安全性能评估产生重要影响。因此,研究船舶运动和波浪载荷的非线性特性,对于超大型集装箱船的设计具有重要价值。
边界元法(BEM)作为一种高效的数值分析方法,已成为研究船舶水动力问题的重要手段。近年来,国内外众多学者致力于通过边界元法解决船舶水动力学中的复杂问题。例如,Sun等[1]采用耦合CFD-FEM方法对一艘6 750 TEU集装箱船的非线性水弹性效应进行了研究;Wang等[2]采用基于广义泰勒展开边界元法(TEBEM)的非线性三维面元法,对集装箱船的水弹性问题进行了一系列数值模拟;Datta等[3]采用耦合边界元−有限元法(BEM-FEM)对某集装箱船进行了时域水弹性效应分析;Lee等[4]基于高阶边界元法(HOBEM)和高阶壳单元有限元法(FEM),采用三维直接耦合方法,提出了一种分析稳态船舶水弹性的新方法;Chen等[5]采用分区的CFD和FEM双向耦合求解器,有效处理了流固耦合问题;Ling等[6]采用基于扩展边界积分法的三维频域水弹性方法,对心形超大型漂浮旅游平台弹性结构进行了不规则频率和水共振分析,并对其极限载荷进行了预测。
由于边界元法方法求解难度较高且适用范围较狭窄,给实际分析研究带来了一定的困难。因此,近处来,三维水弹性力学理论逐渐成为研究航行船舶水动力学问题热门方向。在时域处理方法中,三维水弹性力学理论主要分为3类:时域自由面格林函数法、Rankine面元法和多域法。
Chen等[7-9]利用Rankine面元法对13 000 TEU和15 000TEU的集装箱船进行非线性水弹性响应分析,研究了不同载荷分量随波向的变化规律,并基于三维非线性水弹性理论,计算了某散货船在有无砰击作用下的弯矩响应。为准确预报船舶在规则波中航行时的波浪诱导运动和载荷,Jiao等[10-12]建立了全耦合三维时域非线性水弹性理论,并分析了大型弹性船舶在不规则航道中的水弹性运动和载荷响应进行预报,分析大型弹性船舶在不规则波中航行时的非线性水弹性运动和载荷响应。Ni等[13]运用广义二阶波浪力理论在频域内计算海浪引起的二阶非线性响应,并通过脉动源格林函数和平移−脉动源格林函数研究了180 000 DWT大型散货船在有/无前进速度时线性力对波浪响应和载荷的影响。Zhang等[14]提出基于三维频域格林函数和动量定理的耦合时域水弹性方法,对10 000 TEU集装箱船的船舯剖面垂向弯矩进行了非线性长短期分析。王思雨[15]以210 000 TEU集装箱船为例进行计算,研究超大型集装箱船在不同航速和浪向下非线性载荷特性及船体水弹性响应规律,并对船体弹振与颤振现象进行分析。周文俊[16-17]对多域法中的内域部分进行改进,考虑入射波耦合项影响,提出新的多域法计算模型,并以5艘具有不同外形特征的船型为对象,计算其在波浪中运动响应。张楷弘[18]建立了有航速大外飘船舶的时域非线性水弹性理论计算方法,并开展了大外飘船舶二、三维混合时域非线性水弹性计算研究。徐志亭等[19]结合雨点计数法,研究了非线性砰击载荷对大外飘型船舶疲劳损伤的影响。罗凯等[20]基于三维水动力理论,充分考虑各种非线性效应,采用设计波法进行了波浪载荷预报。
对于大型集装箱船和军舰等大外飘船舶,采用三维时域格林函数方法不仅计算耗时,且结果往往也不太稳定。此外,采用Rankine源和数值海岸或阻尼层方法时,其计算稳定性与自由面范围、网格大小、数值阻尼系数和来波波长相关,且存在数值稳定性问题。为此,本文拟采用内外区域匹配法(inner and outer region matching method,IORM)计算流体场的速度势和波浪激励力,并利用自主研发的OpenWALAS[21]软件对一艘20 000 TEU集装箱船的运动响应及剖面载荷进行评估,分析入射波力、静水恢复力等非线性因素对船舶运动与船体剖面波浪载荷的影响。
1. 三维时域非线性水弹性力学理论基础
1.1 内外区域匹配法
本文提出一种内外区域匹配法( IORM),用于计算船舶流场的速度势和波浪激励力。该方法结合了时域格林函数和Rankine源技术:首先,在船体一定距离处构造一个虚拟的控制面包围整个船体,形成内域;然后采用Rankine源法求解整个内域流场,同时在外域采用三维时域函数方法计算整个外域流场。通过在控制面上匹配内域和外域的速度势及其导数。
IORM的数学模型如图1所示,其中内域ΩI由物面Sb、自由面SF和控制面SC组成,而外域ΩII则包含控制面SC和无限流场。图中,内域表面S(包括物面Sb、自由面SF和控制面SC)的方向均指向内域ΩI的外部,其中n为面元的单位法向方向。
该方法中整个流域内任意位置的速度势可以表示为
\left\{ \begin{aligned} & {\varPhi }^{\mathrm{I}}\left({\boldsymbol{x}};t\right) = {\phi }^{\mathrm{I}}\left({\boldsymbol{x}};t\right) + {\phi }_{0}\left({\boldsymbol{x}};t\right),&& {\varOmega }_{\mathrm{I}}\\& {\varPhi }^{\text{II}}\left({\boldsymbol{x}};t\right) = {\phi }^{\text{II}}\left({\boldsymbol{x}};t\right) + {\phi }_{0}\left({\boldsymbol{x}};t\right),&& {\varOmega }_{\text{II}} \end{aligned} \right. (1) 式中:x为质点所处空间函数;t为时间; {\varPhi ^{\text{I}}} , {\varPhi ^{{\text{II}}}} 分别为内、外域流场速度势; {\phi ^{\text{I}}} , {\phi ^{{\text{II}}}} 分别为内、外域流场除入射波速度势外的部分; {\phi _0} 为入射波速度势,在参考坐标系中,其可表示为
{\phi _0}\left( {x,y,{\textit{z}};t} \right) = \frac{g}{\omega }{{\text{e}}^{k{\textit{z}}}}\sin \left[ {k\left( {x\cos \beta + y\sin \beta } \right) - {\omega _{\text{e}}}t} \right] (2) 式中: \omega 为波浪自然频率; {\omega _{\text{e}}} 为遭遇频率, {\omega _{\text{e}}} = \omega - k{U_0}\cos \beta ,其中U0为航速,k为波数,β为浪向角;g为重力加速度。
流场内域中辐射速度势采用Rankine源法建立相应的边界积分方程:
\begin{split} & {2{\text{π}} \phi _{\rm{r}}^{\text{I}}\left( {p,t} \right) + \iint\limits_S {\phi _{\rm{r}}^{\text{I}}\left( {q,t} \right)\frac{{\partial \left( {1/r} \right)}}{{\partial {n_q}}}{\text{d}}s} = } \iint\limits_S \frac{1}{r}\frac{{\partial \phi _{\rm{r}}^{\text{I}}\left( {q,t} \right)}}{{\partial {n_q}}}{\text{d}}s\\&\qquad\qquad\qquad p, q \in {S_{\text{C}}} + {S_{\text{F}}} + {S_{\text{b}}}\\[-1pt] \end{split} (3) 式中: \phi _{\rm{r}}^{\text{I}} 为内域辐射势;s为流场面域; {n_q} 为场点单位法向;r为场点q(ξ,η,ζ)与原点p(x,y,z)之间的距离。
采用脉冲响应方法时,可以将流域中第i阶模态的辐射势 {\phi _{i}}\left( {p,t} \right) 分解为瞬时效应与记忆效应。使用时域格林函数求解船体速度势并进行详细的推导,水线项积分可以变形为
I = - \frac{{U_0^2}}{g}\int\limits_0^t {{\text{d}}\tau } \oint\limits_\varGamma {\left[ {{\chi _{\rm{r}}}\left( {q,\tau } \right)\left( {{n_1}\frac{{\partial \tilde G}}{{\partial \xi }} + {n_1}{n_2}\frac{{\partial \tilde G}}{{\partial l}} + \tilde G\frac{{\partial \left( {{n_1}{n_2}} \right)}}{{\partial l}}} \right)} \right]{\text{d}}l} - \frac{{2{U_0}}}{g}\int\limits_0^t {{\text{d}}\tau } \oint\limits_\varGamma {{n_1}\tilde G\frac{{\partial {\chi _{\rm{r}}}}}{{\partial \tau }}{\text{d}}l} (4) 式中: {\chi _{\rm{r}}} 表示记忆效应项;l, {\boldsymbol{n}} = \left\{ {{n_1},{\text{ }}{n_2},{\text{ }}{n_3}} \right\} 分别为船体水线及其法向分量;\tilde G 为三维时域格林函数;\tau 为积分时间;\varGamma 为船体水线。
内域 {\varOmega _{\text{I}}} 中求解物面 {S_{\text{b}}} 、自由面 {S_{\text{F}}} 和控制面 {S_{\text{C}}} 上绕射速度势 \phi _{\text{D}}^{\text{I}}\left( {p,t} \right) 的积分方程为
2{\text{π}} \phi _{\text{D}}^{\text{I}}\left( {p,t} \right) + \iint\limits_S {\phi _{\text{D}}^{\text{I}}\left( {q,t} \right)\frac{{\partial \left( {1/r} \right)}}{{\partial {n_q}}}{\text{d}}s} = \iint\limits_S {\frac{1}{r}\frac{{\partial \phi _{\text{D}}^{\text{I}}\left( {q,t} \right)}}{{\partial {n_q}}}{\text{d}}s} (5) 外域 {\varOmega _{{\text{II}}}} 中求解控制面 {S_{\text{C}}} 上源点绕射速度势 \phi _{\text{D}}^{{\text{II}}}\left( {p,t} \right) 的积分方程为:
\begin{split} & - 2{\text{π}} \phi _{\text{D}}^{{\text{II}}}\left( {p,t} \right) + \iint\limits_S {\phi _{\text{D}}^{{\text{II}}}\left( {q,t} \right)\frac{\partial }{{\partial {n_q}}}\left( {\frac{1}{r} - \frac{1}{{{r_1}}}} \right){\text{d}}{S_q}} = \iint\limits_S {\left( {\frac{1}{r} - \frac{1}{{{r_1}}}} \right)\frac{{\partial \phi _{\text{D}}^{{\text{II}}}\left( {q,t} \right)}}{{\partial {n_q}}}{\text{d}}{S_q}} + \\&\quad \int\limits_{ - \infty }^t {{\text{d}}\tau } \iint\limits_S {\left[ \tilde G\left( {p,q;t - \tau } \right)\frac{{\partial \phi _{\text{D}}^{{\text{II}}}\left( {q,\tau } \right)}}{{\partial {n_q}}} - \phi _{\text{D}}^{{\text{II}}}\left( {q,\tau } \right)\frac{\partial }{{\partial {n_q}}}\tilde G\left( {p,q;t - \tau } \right) \right]{\text{d}}{S_q}} - \\&\;\; \frac{1}{g}\int\limits_{ - \infty }^t {{\text{d}}\tau } \oint\limits_\varGamma {\left\{ {U_0^2\left[ \tilde G\left( {p,q;t - \tau } \right)\frac{{\partial \phi _{\text{D}}^{{\text{II}}}\left( {q,\tau } \right)}}{{\partial \xi }} - \phi _{\text{D}}^{{\text{II}}}\left( {q,\tau } \right)\frac{\partial }{{\partial \xi }}\tilde G\left( {p,q;t - \tau } \right) \right]} \right.} - \\&\qquad \left. {{U_0}\left[ \tilde G\left( {p,q;t - \tau } \right)\frac{{\partial \phi _{\text{D}}^{{\text{II}}}\left( {q,\tau } \right)}}{{\partial \tau }} - \phi _{\text{D}}^{{\text{II}}}\left( {q,\tau } \right)\frac{\partial }{{\partial \tau }}\tilde G\left( {p,q;t - \tau } \right) \right]} \right\}{\text{d}}\eta \end{split} (6) 式中:r1为源点与场点镜像点距离;Sq为场点面积;\phi _{\text{D}}^{{\text{II}}}\left( {q,\tau } \right) 场点绕射速度势; \xi , \eta 分别为水线局部坐标系的切向与法向。
因在某一时刻绕射势和绕射势的导数已趋于0,故在实际计算中并不需要从 - \infty 开始,只需选取合适的负时刻开始计算即可。另外,参考辐射势求解中水线项积分的推导方法和初始条件,可得绕射势的水线项积分为
\begin{split} & I = - \frac{{U_0^2}}{g}\int\limits_{ - \infty }^t {{\text{d}}\tau \oint\limits_\varGamma {\left[ \begin{gathered} - n_1^2\tilde G\frac{{\partial {\phi _{\text{D}}}\left( {q,\tau } \right)}}{{\partial {\boldsymbol{n}}}} + {\phi _{\text{D}}}\left( {q,\tau } \right)\cdot \\ \left( {{n_1}\frac{{\partial \tilde G}}{{\partial \xi }} + {n_1}{n_2}\frac{{\partial \tilde G}}{{\partial l}} + \tilde G\frac{{\partial \left( {{n_1}{n_2}} \right)}}{{\partial l}}} \right) \\ \end{gathered} \right]{\text{d}}l} } - \\&\qquad\qquad\qquad \frac{{2{U_0}}}{g}\int\limits_{ - \infty }^t {{\text{d}}\tau } \oint\limits_\varGamma {{n_1}\tilde G\frac{{\partial {\phi _{\text{D}}}}}{{\partial \tau }}{\text{d}}l} \\[-1pt] \end{split} (7) 1.2 三维时域非线性水弹性响应方程
非线性水弹性力学涉及多个方面,包括结构变形和水动力等。本文将仅考虑与水动力有关的非线性效应,例如由大幅运动和瞬时湿表面引起的非线性入射波浪力和静水恢复力。砰击效应不在本文考虑范围。
时域非线性水弹性响应方程:
\begin{split} & \qquad\quad\left( {{\boldsymbol{a}} + {\boldsymbol{A}}} \right)\ddot {\boldsymbol{q}}\left( t \right) + \left( {{\boldsymbol{b}} + {\boldsymbol{B}}} \right)\dot {\boldsymbol{q}}\left( t \right) + \\& \left( {{\boldsymbol{c}} + {\boldsymbol{C}} + {\boldsymbol{C'}}} \right){\boldsymbol{q}}\left( t \right) + \int\limits_0^t {\left[ {{\boldsymbol{K}}\left( {t - \tau } \right)} \right]\dot {\boldsymbol{q}}\left( t \right)} {\text{d}}\tau = \end{split} {{\boldsymbol{F}}_{\text{I}}}\left( t \right) + {{\boldsymbol{F}}_{\text{D}}}\left( t \right) + {{\boldsymbol{F}}_{{\text{rst}}}}\left( t \right) + {{\boldsymbol{F}}_{{\text{slm}}}}\left( t \right) (8) 式中:a,b,c,C分别为船体惯性质量矩阵、结构阻尼矩阵、结构弹性恢复力矩阵和静水恢复力矩阵;A,B,C',K分别为附加质量系数、附加阻尼常数、由航速引起的静水恢复力和辐射势脉冲响应函数,均与非定常运动的历史无关,其中A是与船体几何形状、航速、运动和变形模态相关的函数,B和C'是仅依赖于航速 {U_0} 与船型的常数,K包含了一切流体响应的记忆部分,是与物体几何形状、航速和时间相关的函数,其与物体的运动历史无关; {\boldsymbol{q}}(t) 为主坐标响应; {{\boldsymbol{F}}_{\mathrm{I}}}(t) , {{\boldsymbol{F}}_{{\mathrm{rst}}}}(t) 分别为考虑大幅运动和瞬时湿表面影响的非线性入射波浪激励力与非线性静水恢复力; {{\boldsymbol{F}}_{\mathrm{D}}}(t) 为绕射波浪激励力; {{\boldsymbol{F}}_{{\mathrm{slm}}}}(t) 为砰击力。
1.3 非线性入射波浪激励力
在线性微幅运动假设下,入射波浪力一般在平均湿表面积分。在考虑恶劣海况下的船舶大幅运动和瞬时湿表面影响后,非线性入射波浪力的第r阶波浪力表达式如下:
{F_{{\text{I}},r}}\left( t \right) = \iint\limits_{{S_{\text{b}}}\left( t \right)} {\boldsymbol{n}} \cdot {\boldsymbol{u}}_{{r}}p\left( t \right){\text{d}}S (9) 式中: {S_{\text{b}}}\left( t \right) ,dS分别为考虑船体瞬时位置与波浪形状后的瞬时湿表面和面积微元;n, {\boldsymbol{u}}_{{r}} 分别为湿表面的法向及模态位移向量; p\left( t \right) 为入射波压力,其可以为一阶线性表达式,也可以为考虑伯努利方程二次项的压力。需要说明的是,不考虑绕射和辐射效应对入射波瞬时波面的影响时,入射波压力的一阶线性表达式如下:
p\left( t \right) = \rho g{{\text{e}}^{k\left( {{\textit{z}} + {\text{i}}\alpha } \right)}}{{\text{e}}^{ - {\text{i}}{\omega _{\text{e}}}t}} (10) 式中: \rho 为流体密度; \alpha = x\cos \beta + y\sin \beta 。
1.4 非线性静水恢复力
在考虑恶劣海况下的船舶大幅运动和瞬时湿表面影响后,静水恢复力表现出了一定的非线性,故其不能再表达成恢复力系数矩阵。时域非线性水弹性响应方程中的静水恢复力为
{F_{{\text{rst}},r}}\left( t \right) = - \rho g\iint\limits_{{S_{\text{b}}}\left( t \right)} {{\boldsymbol{n}} \cdot {{\boldsymbol{u}}_{r}}}\sum\limits_{k = 1}^m {{w_k}} {\text{d}}S (11) 式中: {w_k} 为第k阶模态的z方向位移;m为总模态数。
2. 船舶基本参数及网格敏感性与收敛性分析
2.1 船舶参数
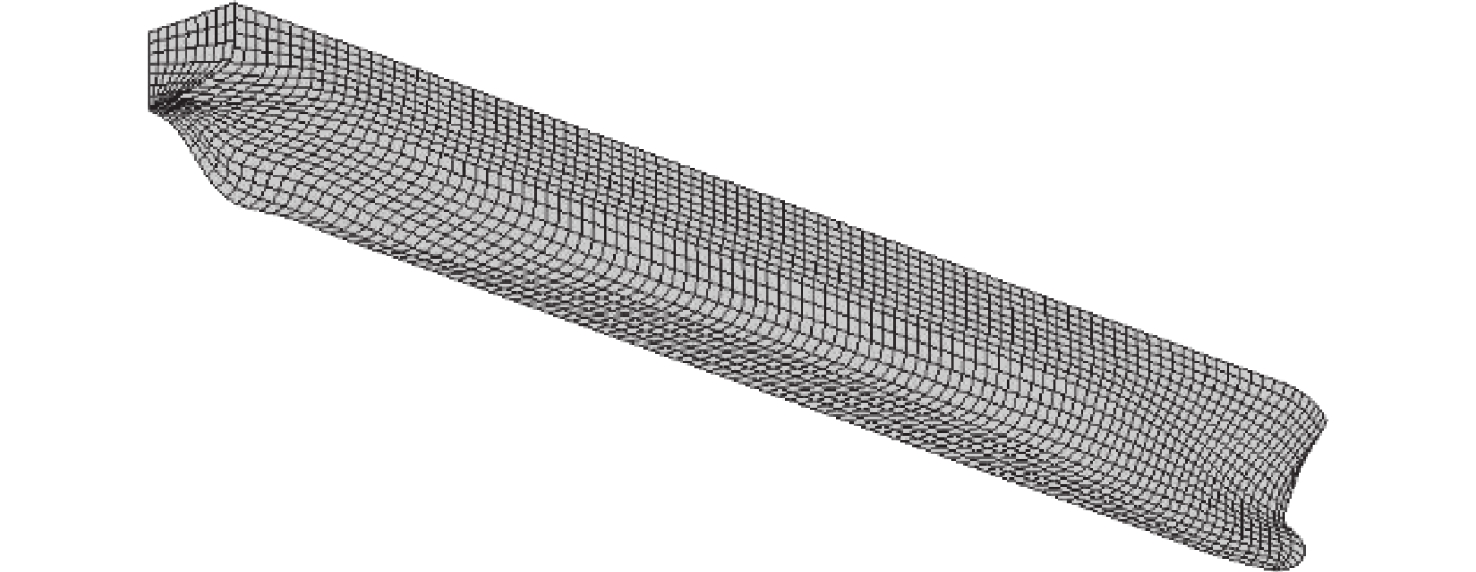
本文选取的计算船舶为20 000 TEU集装箱船,其主尺度参数如表1所示。考虑到船舶的几何对称性,为简化计算,本文采用左半船体模型进行研究。船体水动力网格模型单元共2 045个,如图2所示。模型建模坐标原点取在船尾基线处,其中x轴沿船长方向,船首为正,y轴沿船宽方向,左舷为正,z轴沿船深方向,向上为正。
表 1 船舶主要参数Table 1. Main parameters of ship参数 数值 总长/m 400 垂线间长/m 383 型宽/m 58.6 型深/m 30.5 吃水/m 15.2 排水量/t 2.61×105 重心Zg/m 27.6 重心Xg/m 182.7 2.2 自由面范围的敏感性分析
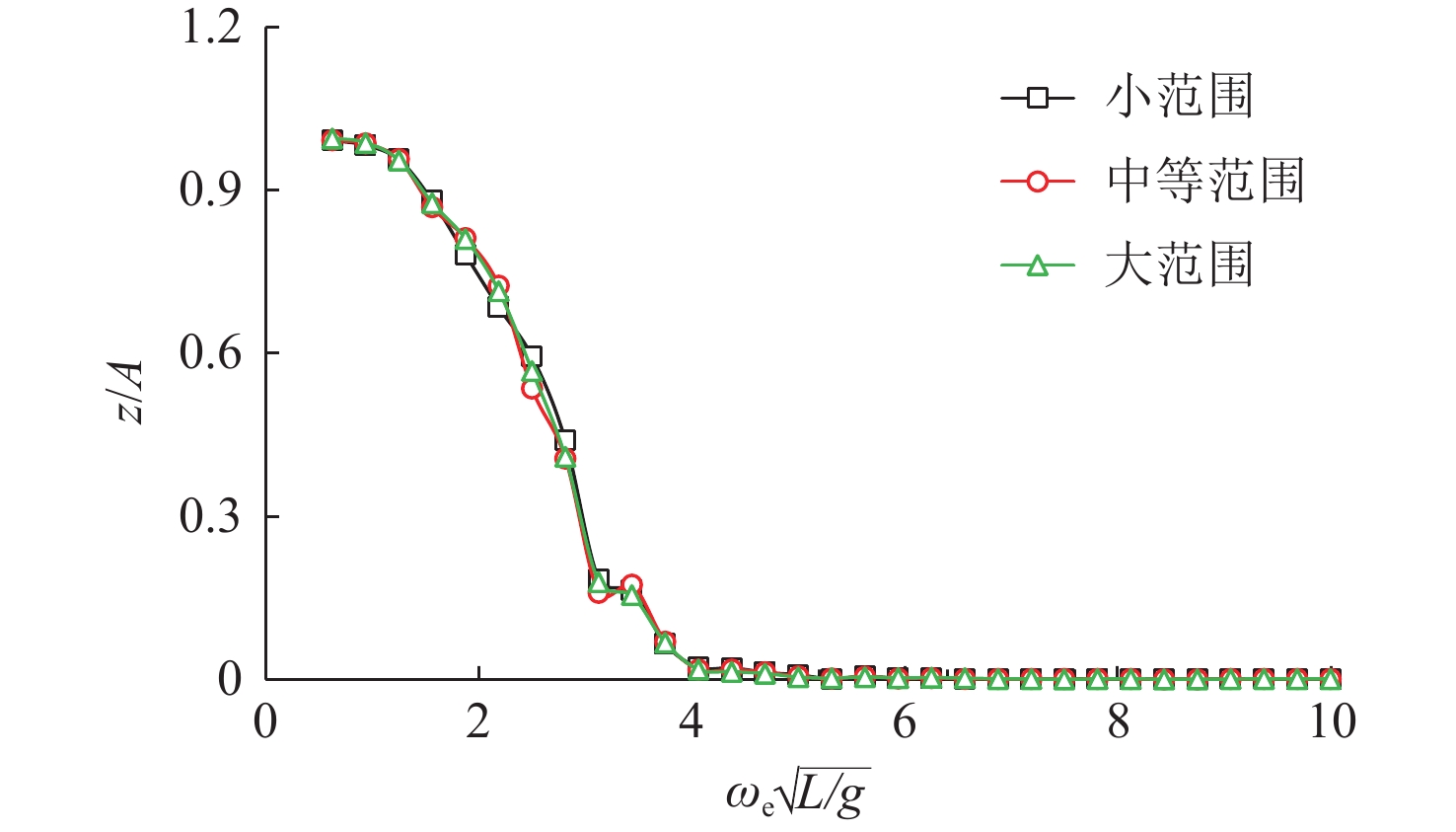
首先,建立IORM模型。为了研究自由面范围的敏感性,设置了3种不同大小的自由面范围,分别命名为小范围自由面、中等范围自由面和大范围自由面,具体尺寸如表2所示。自由面的水动力网格模型如图3所示。基于IORM,采用非线性时域算法,考虑由船体湿表面变化引起的非线性入射波浪激励力和静水恢复力这2种非线性因素,对150º艏斜浪作用下的船舶运动和中横剖面载荷进行计算分析。
表 2 自由面尺寸Table 2. Free surface dimensions类型 自由面长度/m 自由面宽度/m 自由面深度/m 小范围 600 150 30 中等范围 1 200 300 60 大范围 2 400 600 120 图4所示为航速V = 16 kn时的垂荡运动幅值响应传递函数,图5所示为V = 16 kn时的中横剖面垂向弯矩幅值响应传递函数。本文对后文图中变量均进行了无量纲化处理,例如z/A表示垂荡位移,其中z为垂荡位移,A为波幅;Ry/kA表示纵摇转动,其中Ry为纵摇转动,k为波数;Fz/ρgALB表示中横剖面垂向剪力,其中Fz为垂向剪力,L为船体垂线间长,B为船宽;My/ρgAL2B表示中横剖面垂向弯矩,其中My为垂向弯矩; {\omega _{\text{e}}}\sqrt {g/L} 表示遭遇频率; t\sqrt {L/g} 表示时间。由计算结果可以看出,对于运动,无论有无航速,不同自由面的传递函数曲线吻合较好,结果并不随自由面范围的增大而发生明显变化;对于剖面载荷,零航速时传递函数曲线吻合较好,有航速时传递函数曲线在低频阶段吻合较好,在高频阶段存在较大差异,但变化趋势一致。从整体来看,结果具有一致性,自由面范围与船舶水动力计算结果的相关性较小,敏感性较弱,本文方法和自研程序的收敛性较好。从局部来看,中等范围自由面的计算结果与大范围自由面的计算结果更加吻合,但大范围自由面所需计算时间较长,故本文选取中等范围自由面开展后续的研究。
2.3 控制面和自由面网格的收敛性
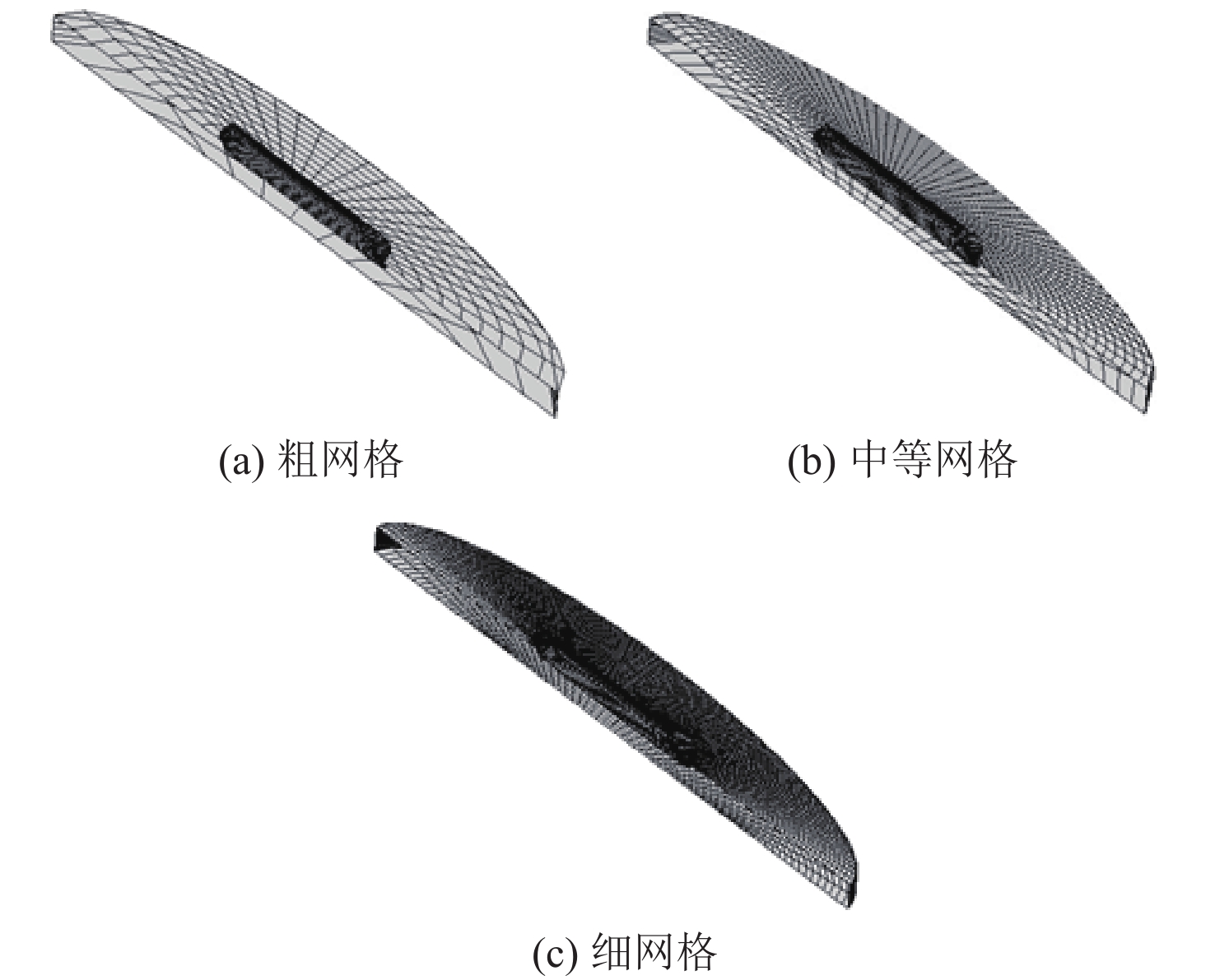
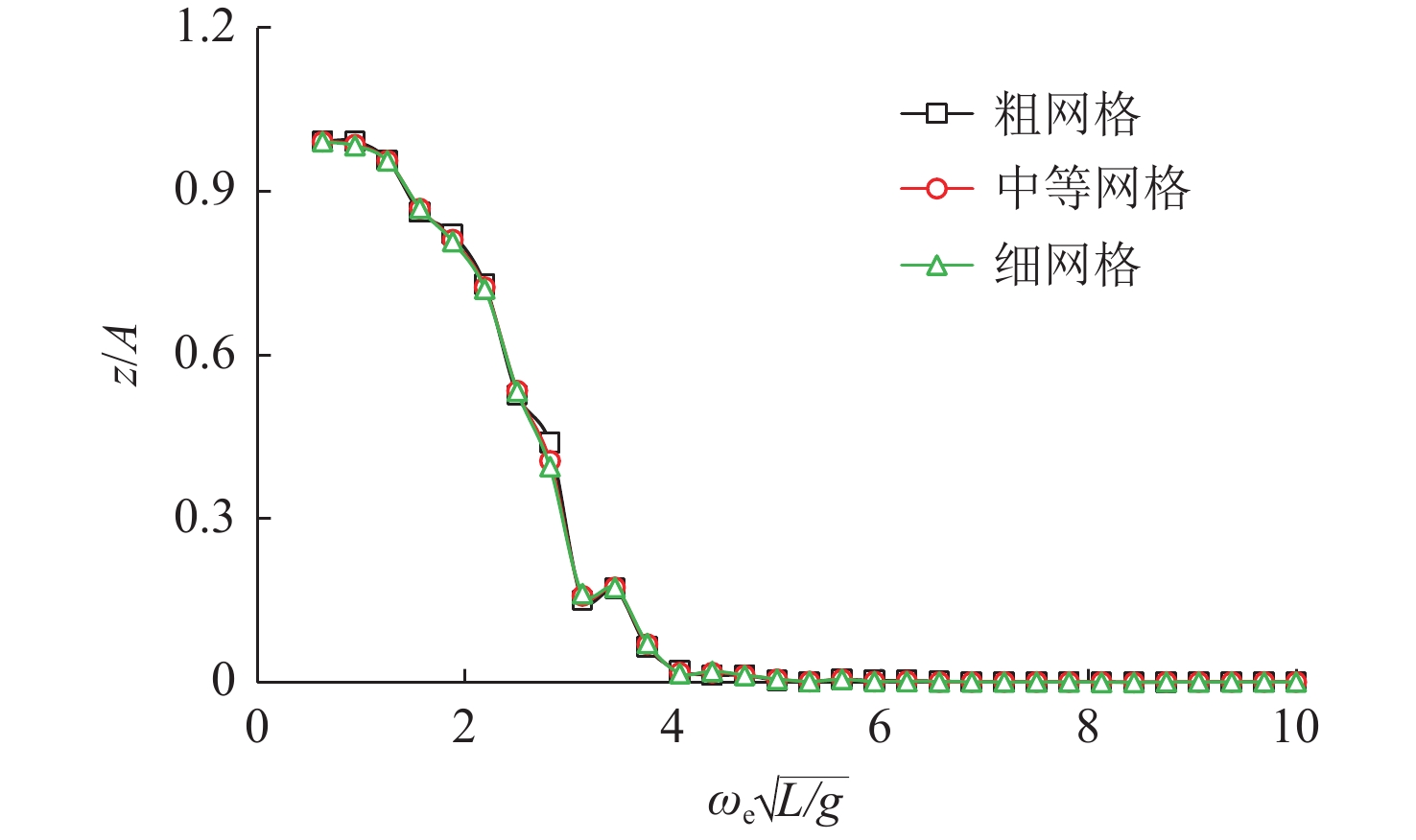
为了研究控制面和自由面网格的收敛性,本文选取中等范围自由面。设定船体网格尺寸不变,设置3种不同大小的控制面和自由面网格,分别命名为粗网格、中等网格和细网格。具体的自由面和控制面面元数如表3所示,网格模型如图6所示。基于IORM方法,采用非线性时域算法,考虑由船体湿表面变化引起的非线性入射波浪激励力和静水恢复力这2种非线性因素,对150°艏斜浪作用下的船舶运动和中横剖面载荷进行计算分析。
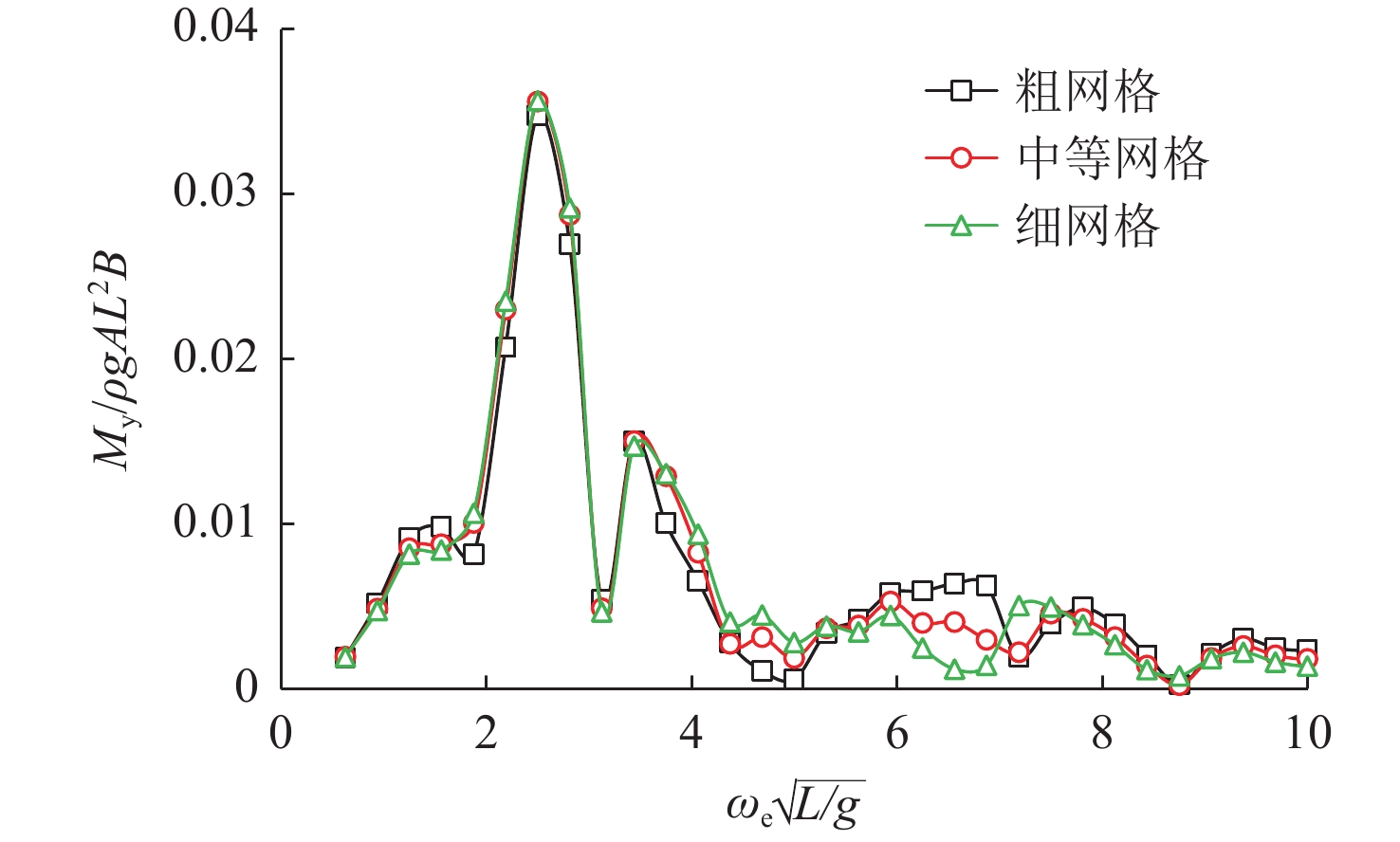
表 3 控制面和自由面网格面元数Table 3. Number of grid elements for control surface and free surface类型 船体面元数 自由面元数 控制面元数 粗网格 2 045 216 81 中等网格 2 045 931 361 细网格 2 045 3 861 1 521 图7所示为V = 16 kn时的垂荡运动幅值响应传递函数,图8所示为V = 16 kn时的中横剖面垂向弯矩幅值响应传递函数。由图可以看出,对于运动,无论有无航速,船舶运动对网格的疏密程度并不敏感,虽然粗网格模型的计算结果相比中等网格和细网格模型存在些许差异,但其变化趋势一致,整体上有着较好的网格收敛性;对于剖面载荷,零航速时3种网格模型的载荷计算结果吻合较好,具有较好的网格收敛性,有航速时3种网格的垂向剪力吻合较好,垂向弯矩在高频阶段存在较大差异。从整体来看,相比粗网格模型,中等网格和细网格模型的计算结果更加吻合,具有更高的计算精度,同时也验证了本文方法和自研程序网格收敛性好的结论。因此,本文选取中等网格模型开展后续的计算工作。
3. 数值验证及分析
3.1 运动与波浪载荷的对比验证
针对零航速工况,本文采用自主研发的OpenWALAS软件和传统刚体假设的耐波性商业软件(AQWA,WASIM,WADAM)研究分析船舶在150°艏斜浪作用下的运动和剖面载荷响应,以验证本文算法的准确性。
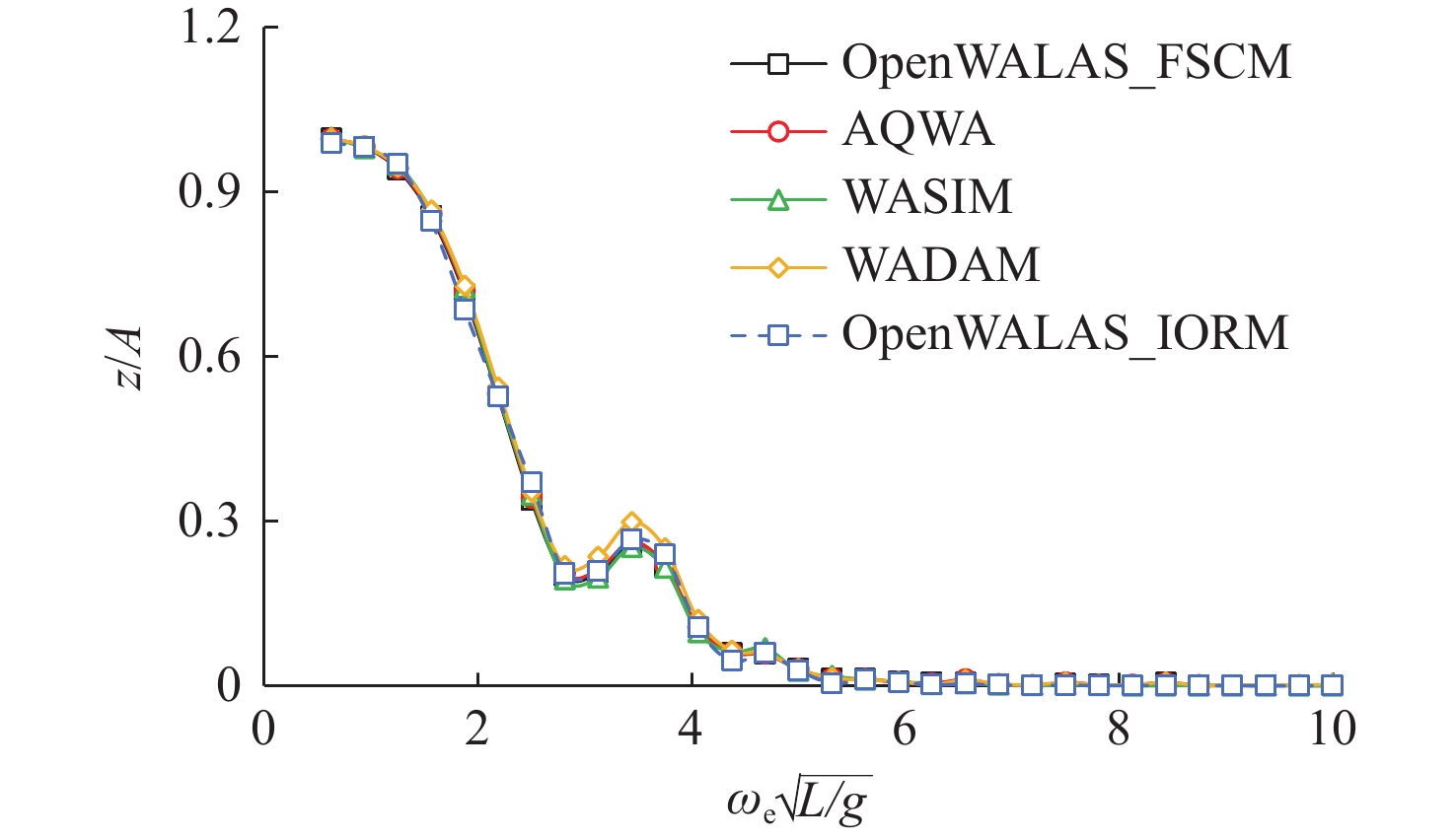
图9所示为垂荡和纵摇运动幅值响应传递函数,图10所示为中横剖面垂向剪力和垂向弯矩幅值响应传递函数。图中,OpenWALAS_FSCM指采用OpenWALAS软件的三维频域计算结果,OpenWALAS_IORM指采用IORM得到的三维时域计算结果。由计算结果可以看出,对于运动,由各个软件所得运动幅值响应传递函数曲线吻合较好;对于剖面载荷,WADAM,AQWA和OpenWALAS_FSCM这3种软件的载荷幅值响应传递函数曲线吻合较好,WASIM与OpenWALAS_IORM这2种软件的载荷幅值响应传递函数吻合较好。这是因为WADAM,AQWA和OpenWALAS_FSCM均基于三维频域方法进行求解,WASIM与OpenWALAS_IORM则基于三维时域方法进行求解。总体来说,虽然各个软件的运动和载荷预报结果在部分区域存在些许差异,但变化趋势一致,整体上吻合较好。
3.2 时域结果的对比验证
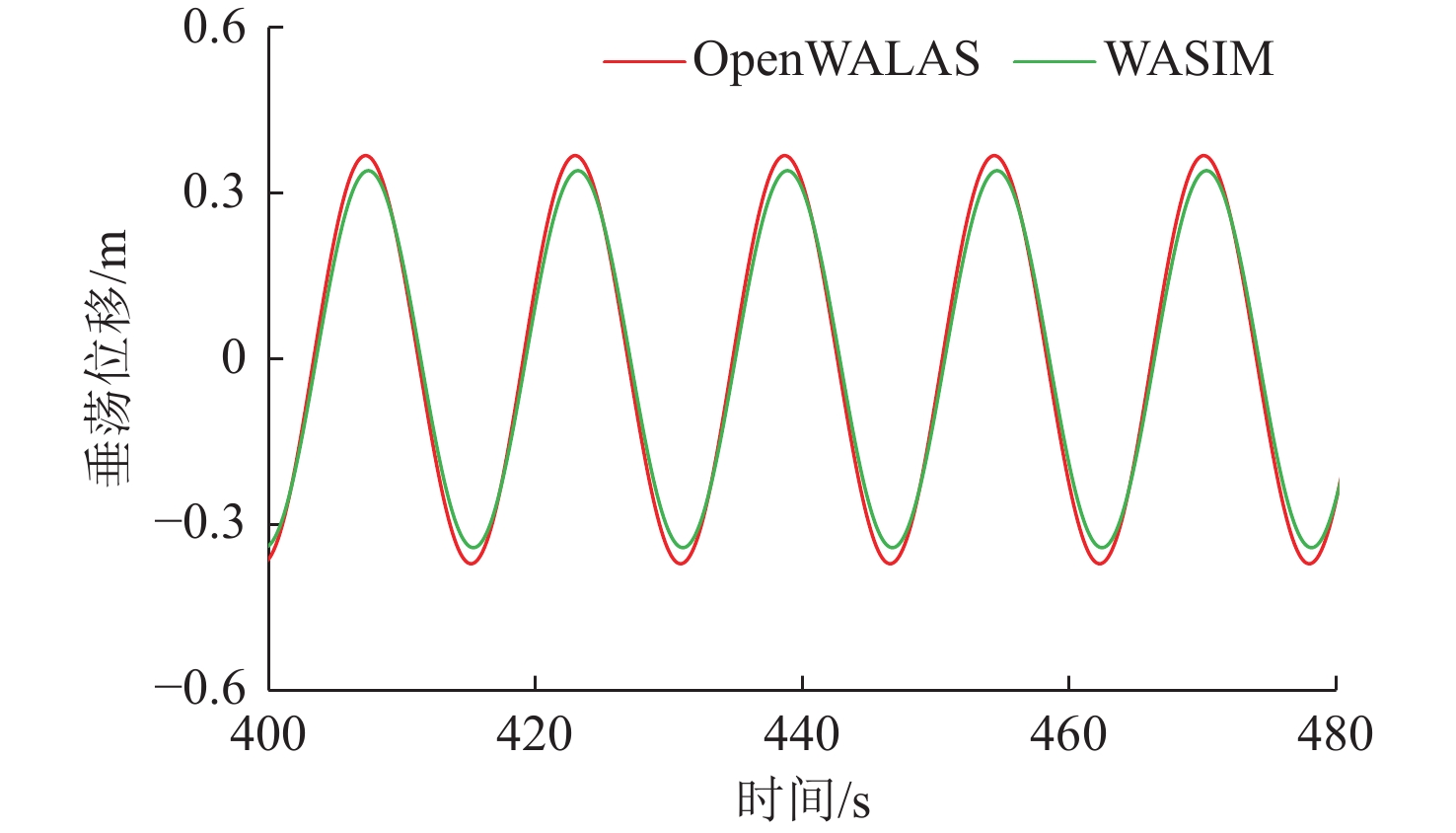
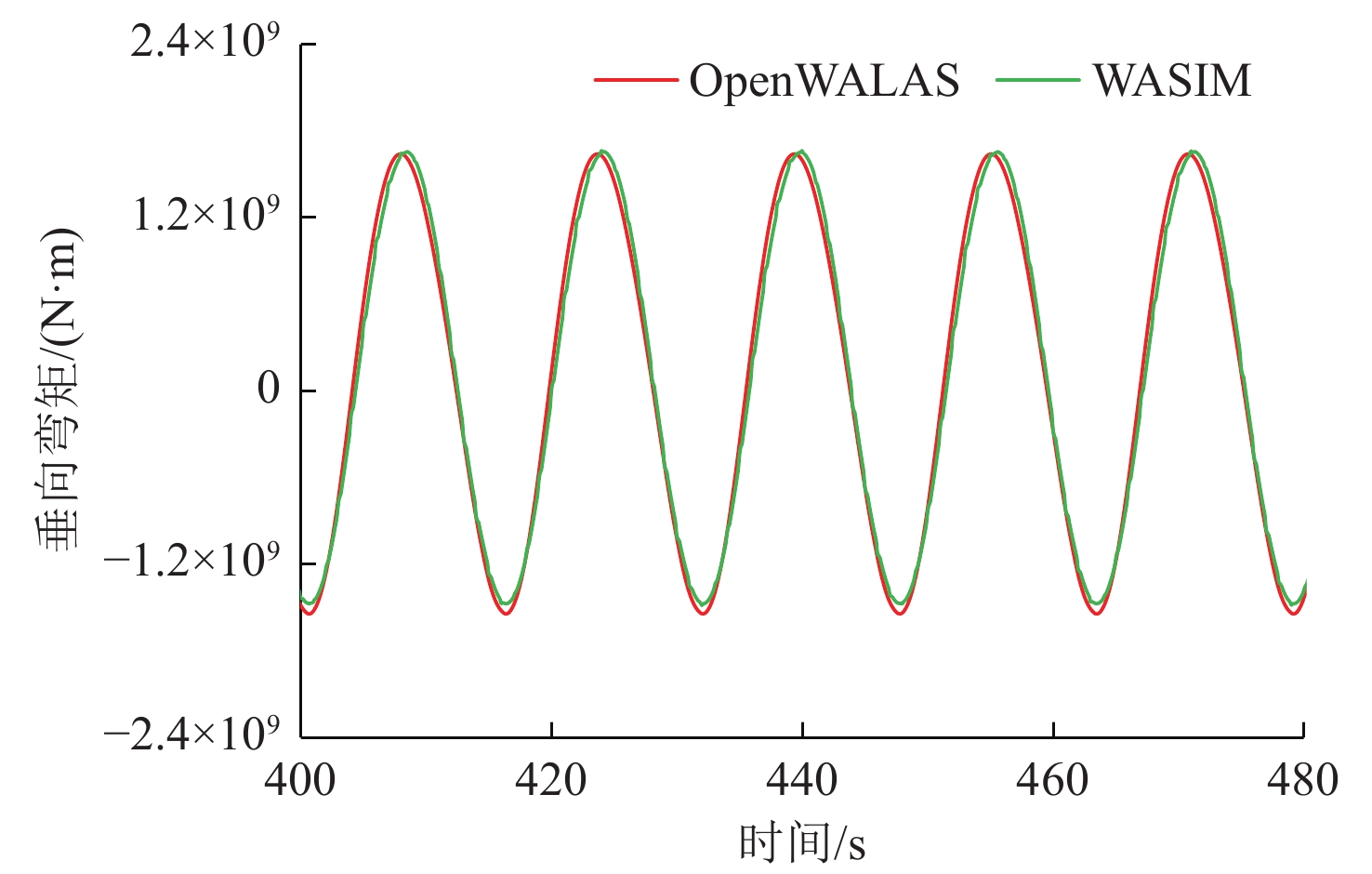
在主流水动力计算软件中,因只有WAISM可以进行非线性全时域计算,所以本节采用软件OpenWALAS和SESAM的WASIM模块对零航速工况下的船舶进行非线性时域计算。图11和图12给出了波高H = 2 m时规则波作用下船舶的运动与波浪载荷时域结果对比。结果显示,采用这2种软件所得计算结果非常一致,其中OpenWALAS的计算结果准确、可靠,可以用于后续的计算分析。
4. 不同波高下非线性因素对波浪载荷的影响
本章采用IORM,分别考虑非线性入射波浪激励力和非线性静水恢复力这2种非线性因素,研究斜浪中不同波高下非线性因素对船舶运动和剖面载荷的影响。
4.1 非线性入射波浪激励力对波浪载荷的影响
当波浪的波长等于船长时,船体内产生的弯矩会使船舶的弯曲最为严重。因此,本节取波长接近于船长的规则波作为入射波,只考虑非线性波浪激励力,计算分析在150º艏斜浪作用下不同波高时的船舶运动和剖面载荷响应,研究非线性波浪激励力对波浪载荷的影响。
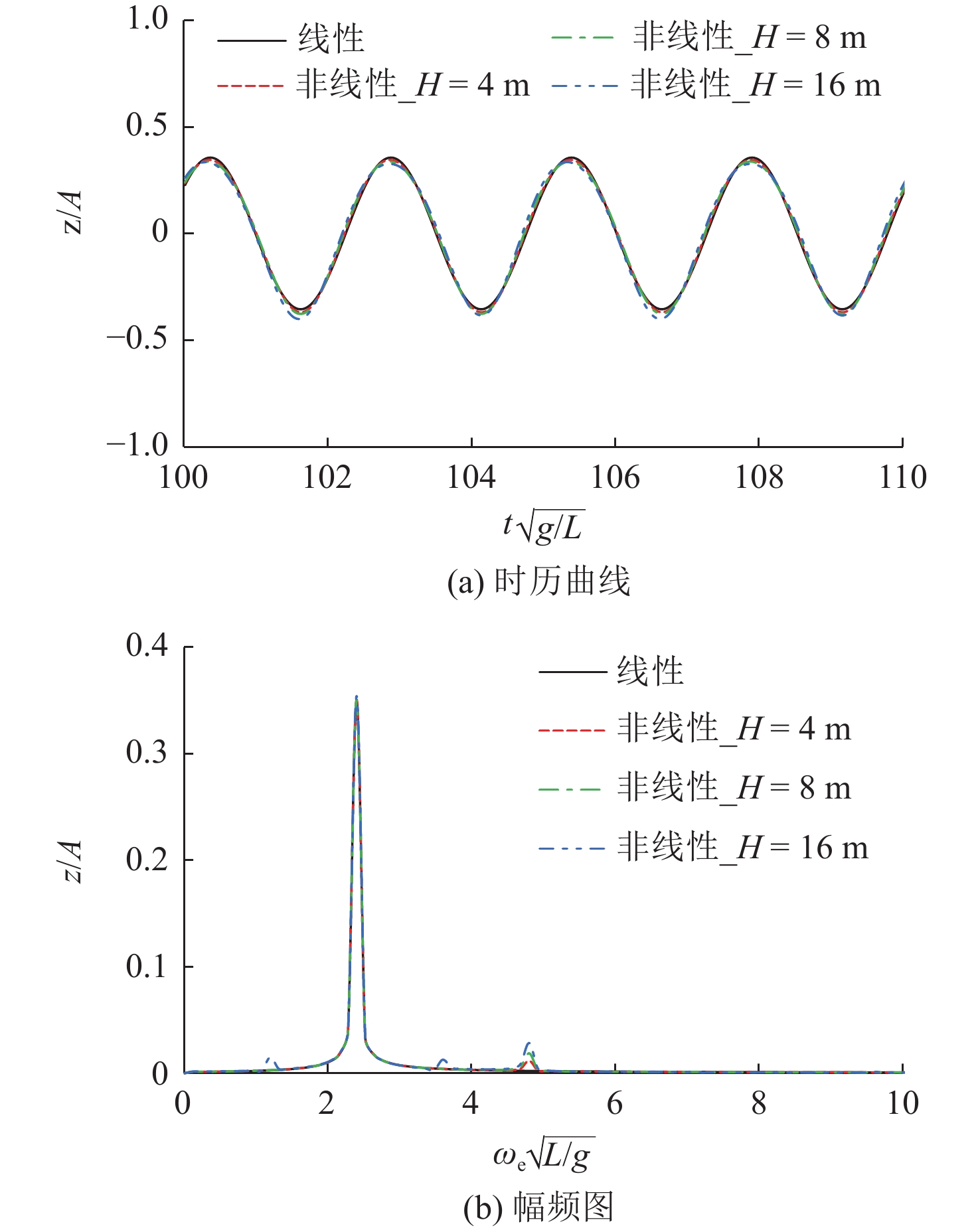
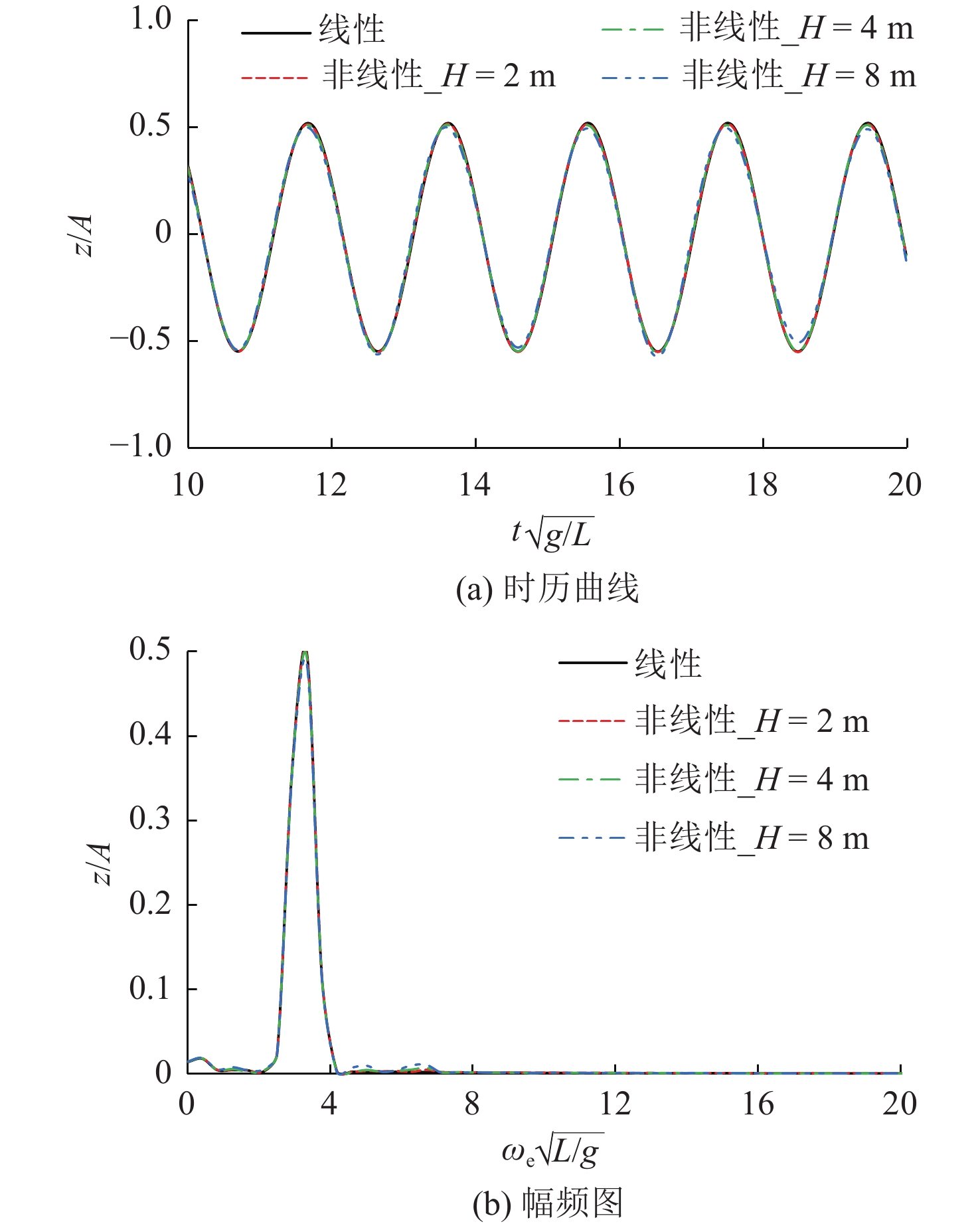
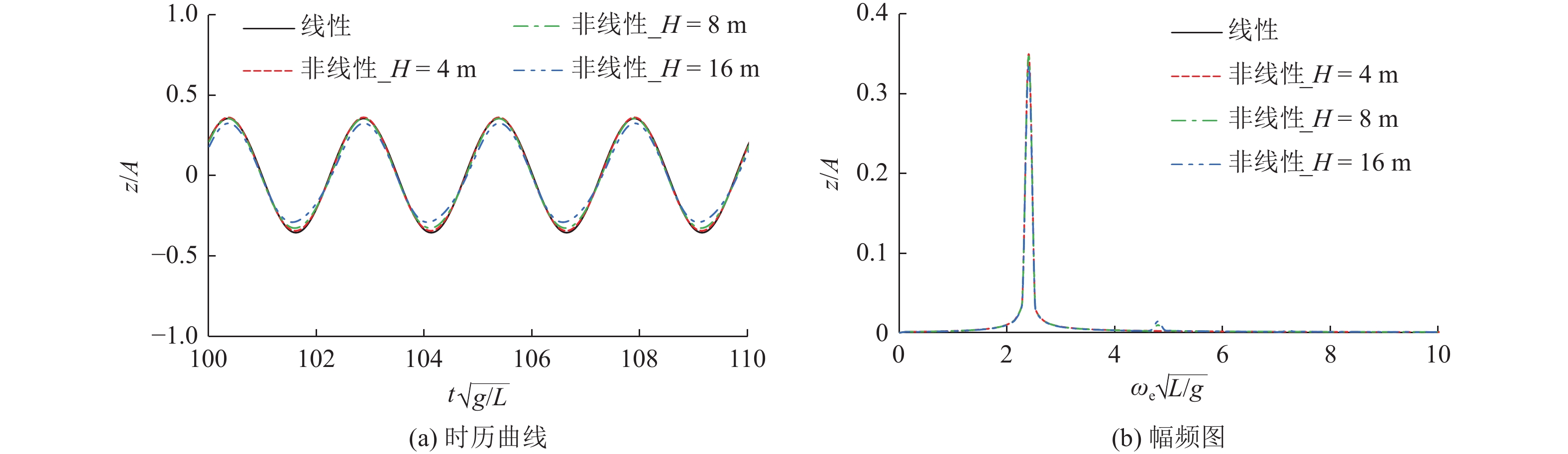
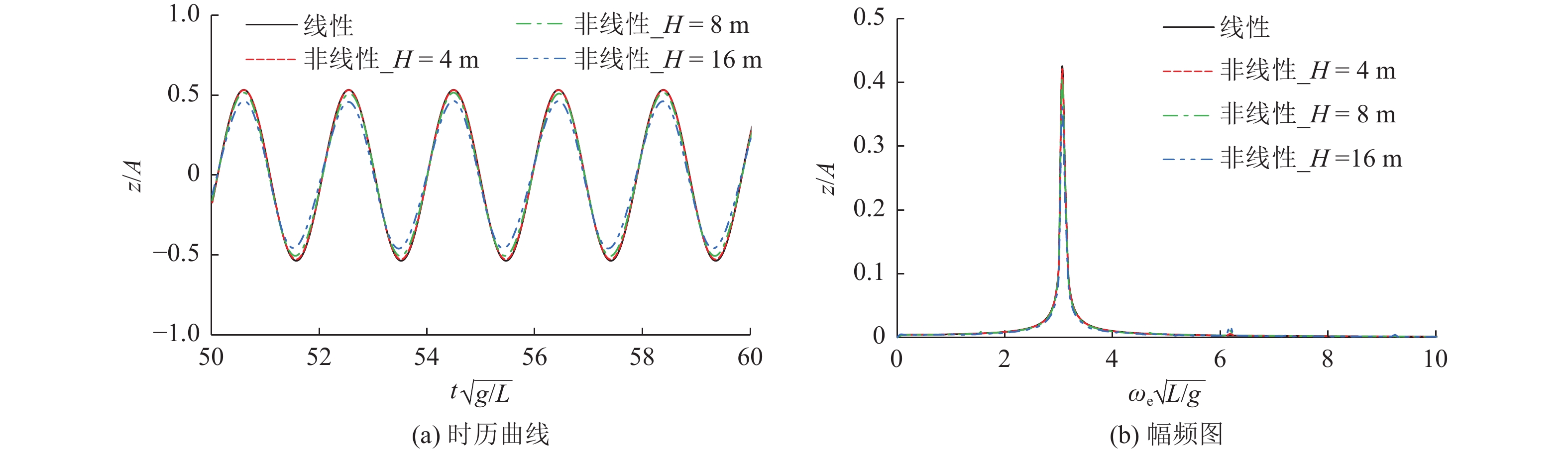
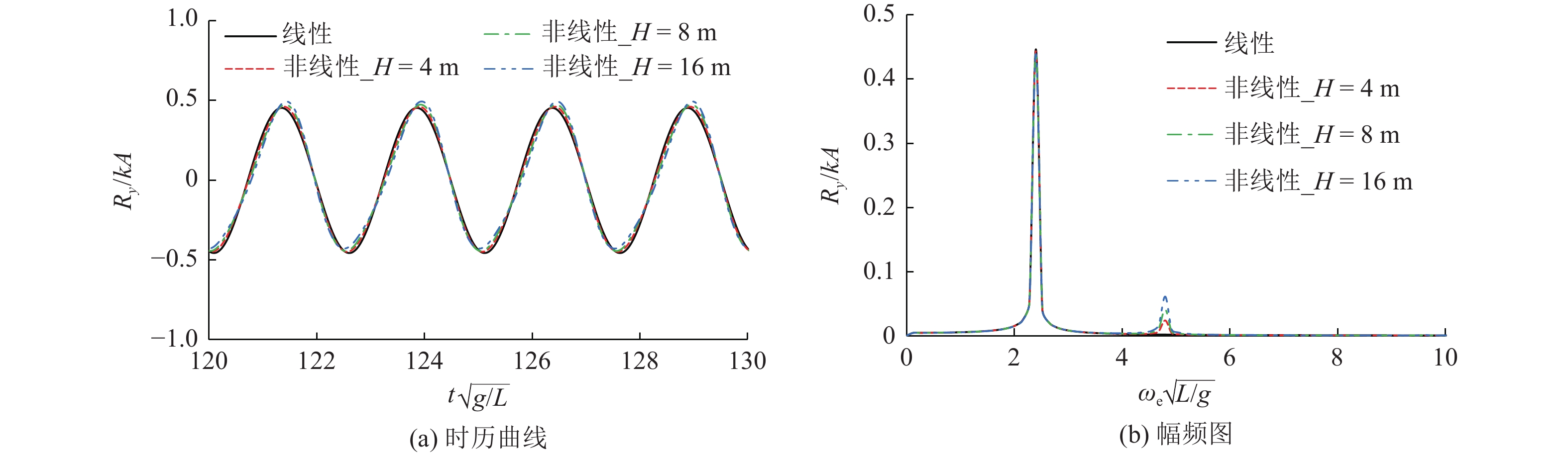
图13~图15所示为不同波高下船舶垂荡运动和纵摇运动响应时历曲线与幅频图。由图可看出,非线性波浪激励力对运动的影响较小。虽然船舶的运动存在轻微的倍频现象(即水动力和载荷响应是遭遇频率的整数倍),且倍频响应幅值随波高的增加而增加,但倍频响应幅值均较小,船舶运动仍呈现为简谐振动,非线性不明显。
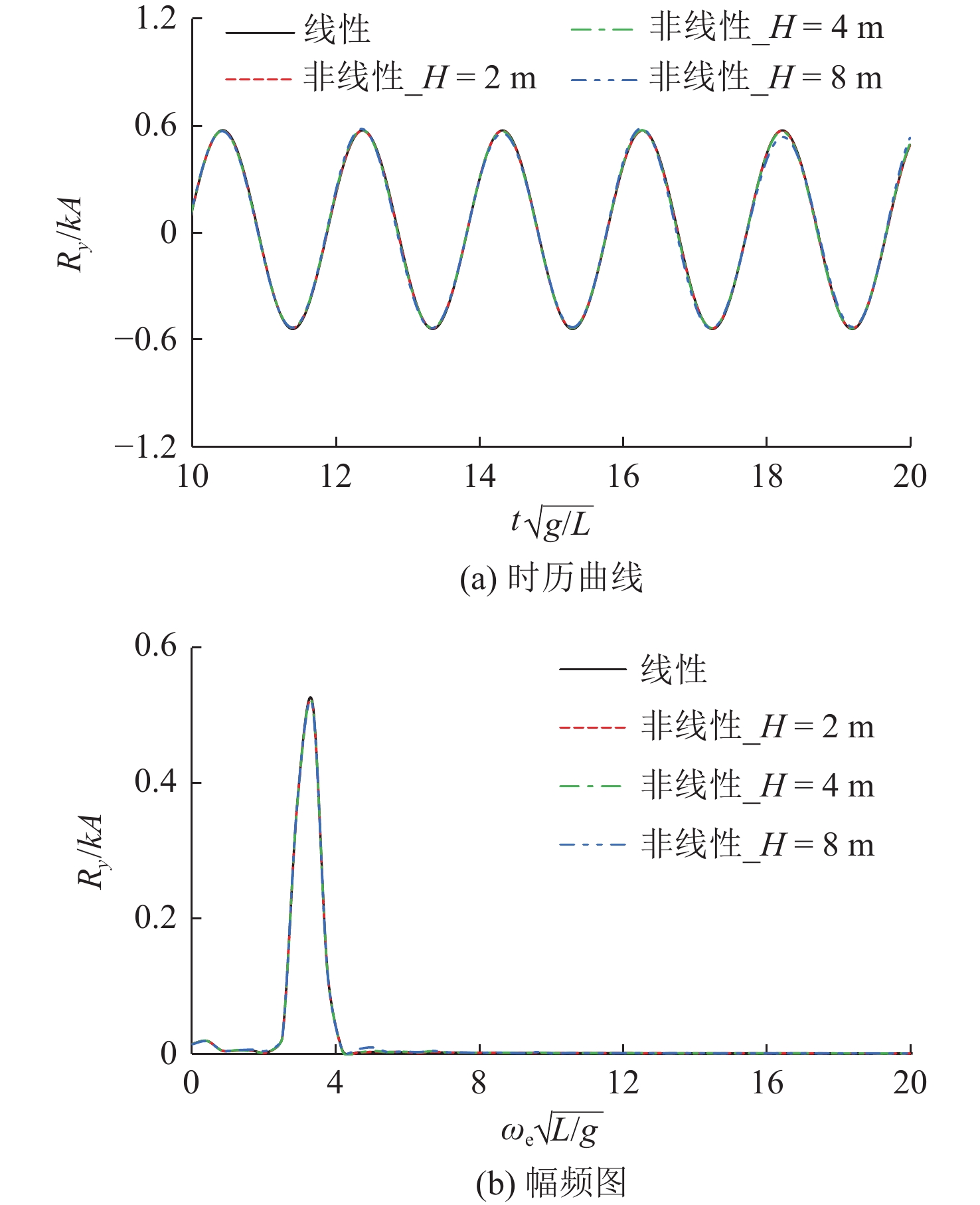
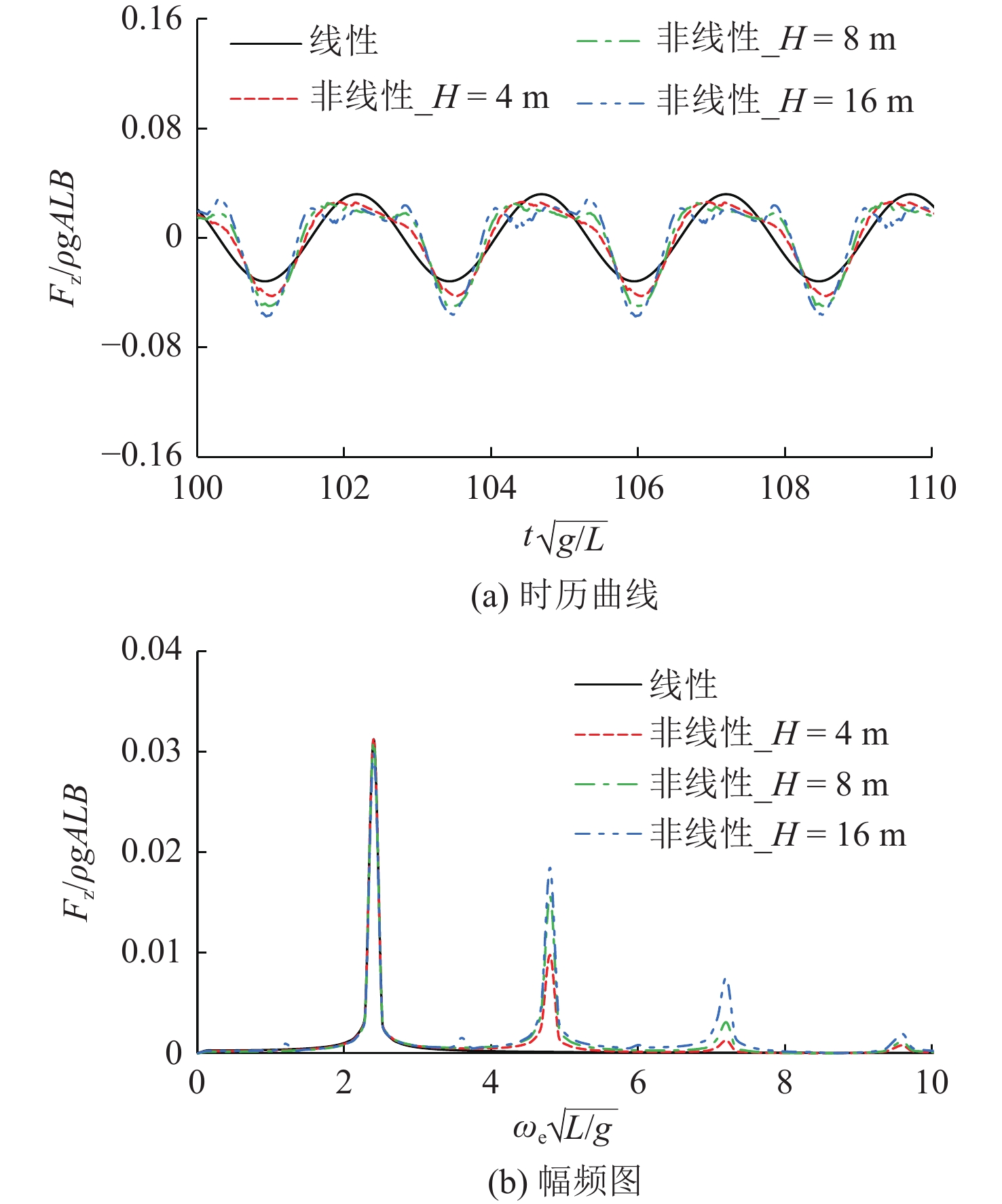
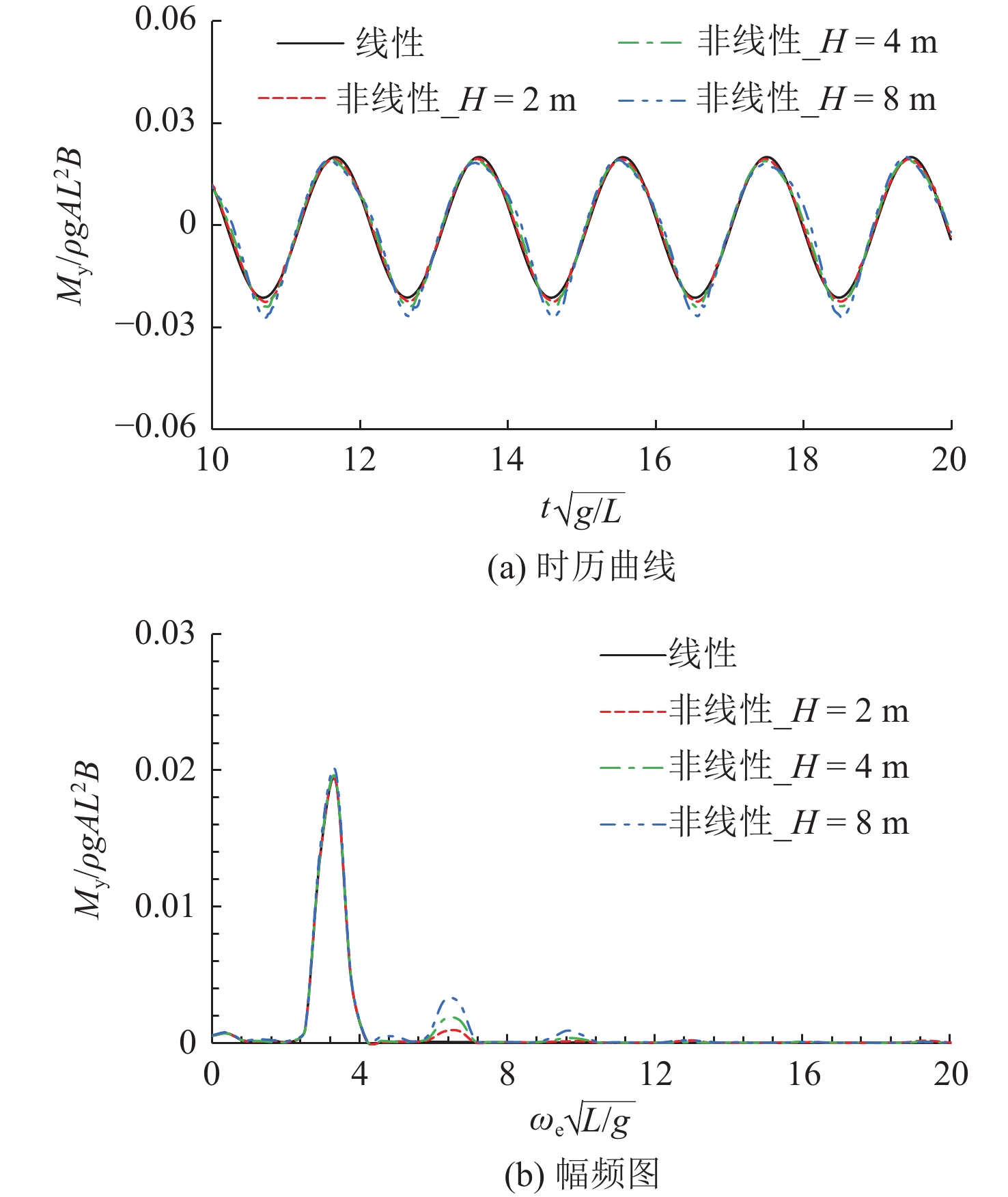
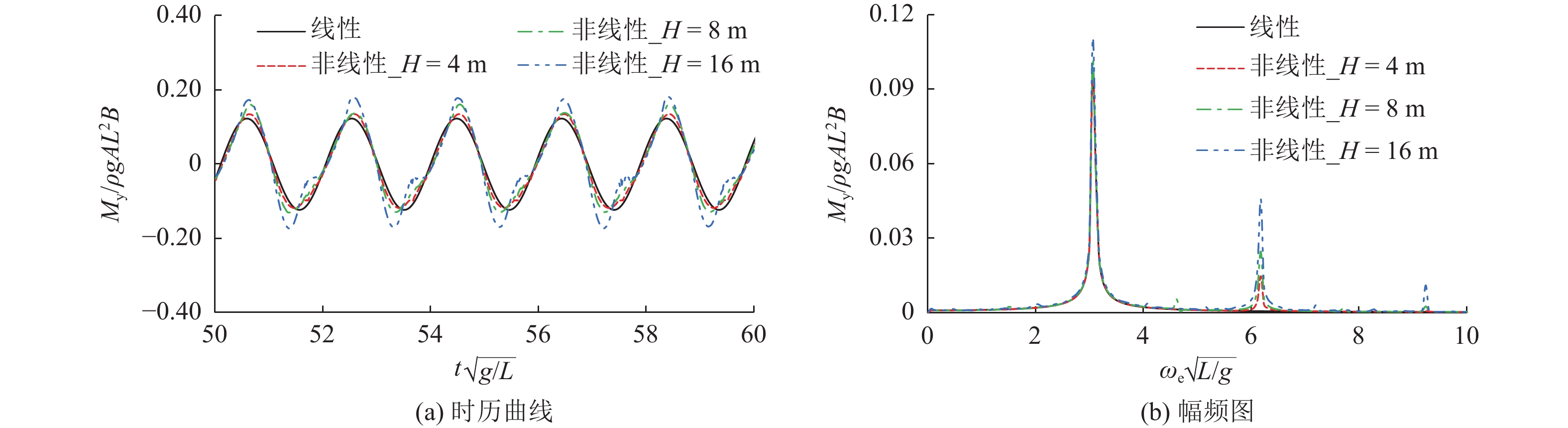
图16~图18所示为不同波高下船舶中横剖面垂向剪力和垂向弯矩的时历曲线与幅频图。由图可看出,无论有无航速,非线性入射波浪激励力对船体中横剖面波浪载荷的影响均较大;入射波浪激励力使得船舶中横剖面的垂向剪力和垂向弯矩出现了明显的多阶倍频响应现象;随着波高的增加,遭遇频率处的运动幅值响应减小,波浪载荷出现了较多倍频的响应成分,这些成分使得船舶载荷的中拱中垂不再对称,非线性响应更加显著。该非线性现象主要是由大幅运动的船体瞬时湿表面变化、斜浪中艏摇运动对遭遇频率和浪向的改变所引起。
综上所述,考虑非线性入射波浪激励力时,船舶运动和波浪载荷的非线性响应主要由倍频效应引起。随着波高的增加,船舶运动和载荷的倍频响应幅值增大,非线性效应愈发明显。在这些复杂响应成分的共同作用下,船舶运动和波浪载荷出现强烈的非线性。相比运动响应,船体剖面波浪载荷响应对非线性波浪激励力更加敏感,其非线性响应现象表现得更加显著。
4.2 非线性静水恢复力对波浪载荷的影响
本节只考虑非线性静水恢复力,计算分析不同波高时的船舶运动和剖面载荷,研究非线性静水恢复力对波浪载荷的影响。
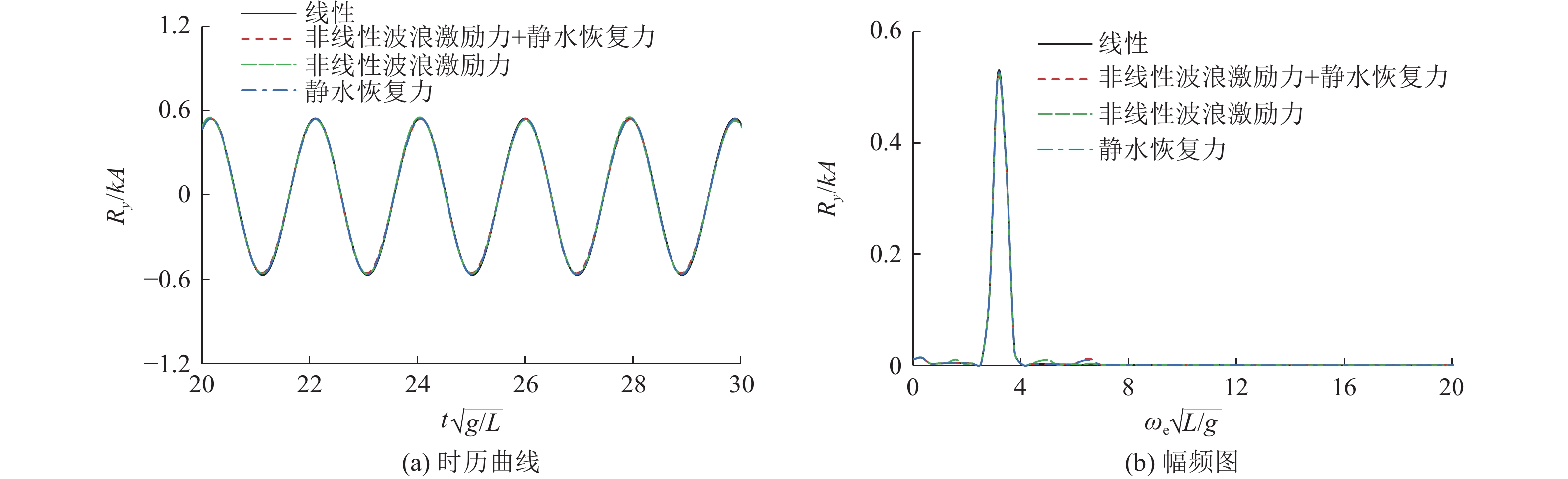
图19~图21所示为不同波高下船舶垂荡运动和纵摇运动的时历曲线与幅频图。由图可以看出,非线性静水恢复力主要影响船舶运动的幅值响应;随着波高的增加,船舶垂荡运动响应幅值减小,船舶运动无明显倍频现象。
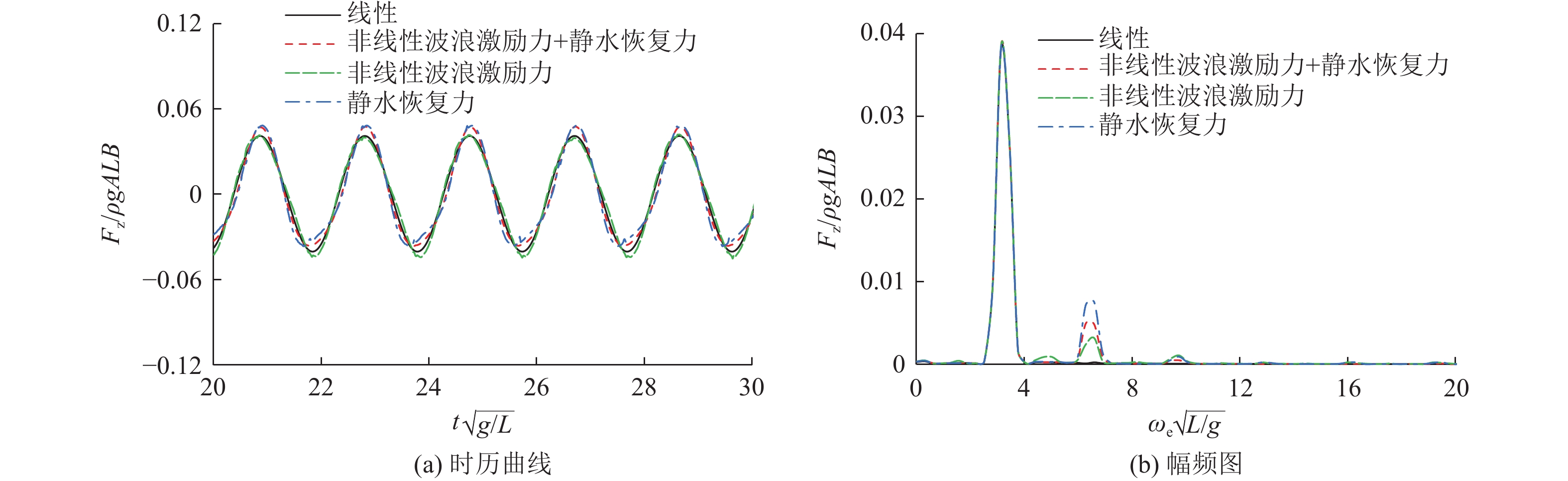
图22~图24所示为不同波高下船舶中横剖面垂向剪力和垂向弯矩的时历曲线与幅频图。由图可以看出,考虑非线性静水恢复力后,船舶载荷主要发生倍频现象;中横剖面的垂向剪力和垂向弯矩出现了明显的多阶倍频现象,多阶倍频使得船舶载荷时历曲线的中拱中垂不再对称;且随着波高的增加,多阶倍频响应幅值增大,波浪载荷表现出显著的非线性。
总体来说,非线性静水恢复力对船舶运动幅值响应的影响较大,对运动的非线性影响较小,对载荷的非线性响应影响较大。
4.3 两种非线性因素共同作用时对波浪载荷的影响
由于船舶与波浪之间的相对运动,船体瞬时湿表面不断发生变化,由湿表面引起的静水恢复力和波浪激励力是船体承受的重要非线性激励力。本节将主要研究这2种非线性因素共同作用时对船体波浪载荷的影响。
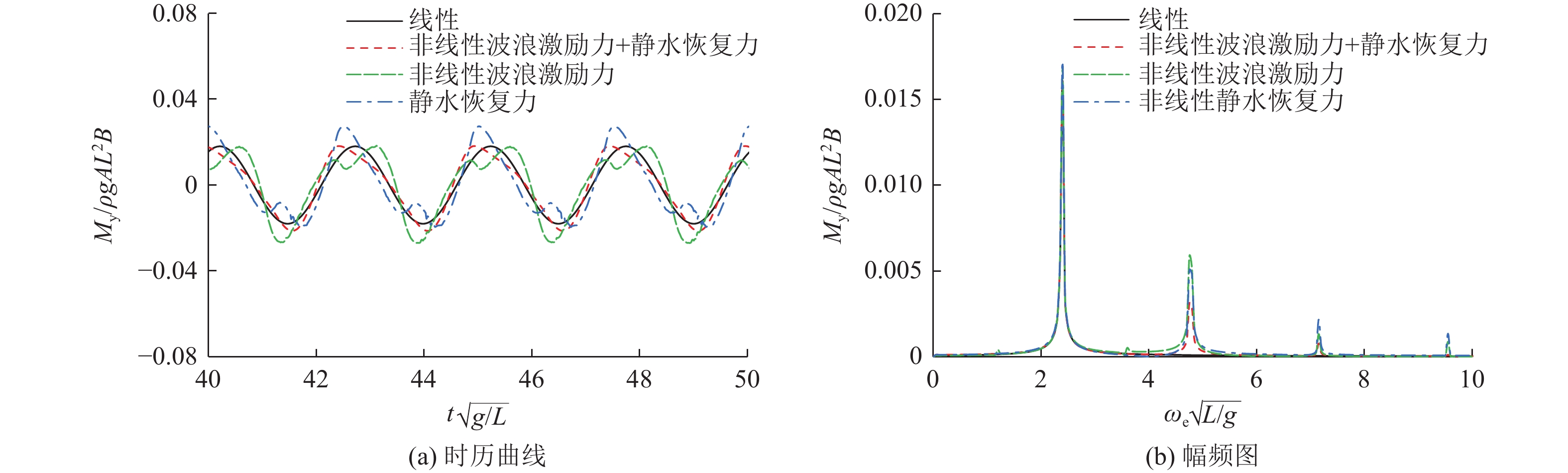
图25和图26所示分别为船舶垂荡和纵摇运动响应的非线性时历响应曲线与幅频图,图27和图28所示分别为船舶中横剖面垂向剪力和垂向弯矩的非线性时历响应曲线与幅频图。由图可看出,当不考虑非线性因素时,无论是运动还是载荷,船舶均未出现非线性倍频响应成分。当考虑2种非线性因素共同作用时,船舶运动仅呈现出轻微的非线性响应,船体剖面载荷非线性响应非常显著,两者均存在不同程度的倍频现象。由计算结果可知,船舶运动和剖面波浪载荷响应的倍频现象是由船体湿表面变化引起的非线性波浪激励力和静水恢复力共同引起。
5. 结 论
基于内外场匹配法(IORM),本文对一艘
20000 TEU集装箱船进行了非线性时域运动和波浪载荷计算,分析了自由面范围敏感性与网格收敛性。在考虑湿表面引起的波浪激励力和静水恢复力这2种非线性因素的基础上,研究了不同波高下非线性因素对船舶运动和剖面波浪载荷的影响,主要得到如下结论:1) 采用IORM计算时,自由面范围与船舶水动力计算结果间的相关性较小,敏感性较弱,适应性强;自由面网格选取中等尺寸时,数值计算结果便已收敛,可见本方法和程序具有较好的收敛性。通过与其他软件计算结果进行综合对比,验证了本文方法和自研程序的准确性与可靠性。
2) 无论有无航速,船舶波浪载荷响应中的非线性成分主要为倍频现象。该倍频现象由船体湿表面变化引起的非线性波浪激励力和静水恢复力共同作用所致。非线性现象主要由大幅运动的船体瞬时湿表面变化、斜浪中艏摇运动对遭遇频域和浪向的改变引起。
3) 船体波浪载荷对非线性因素的敏感性高于运动。随着波高的增加,船舶剖面波浪载荷的响应成分变得更加复杂,其非线性愈发显著,并且在遭遇频率处的波频响应幅值有所减小。
-
表 1 模型工况设计
Table 1 Working conditions design of the model
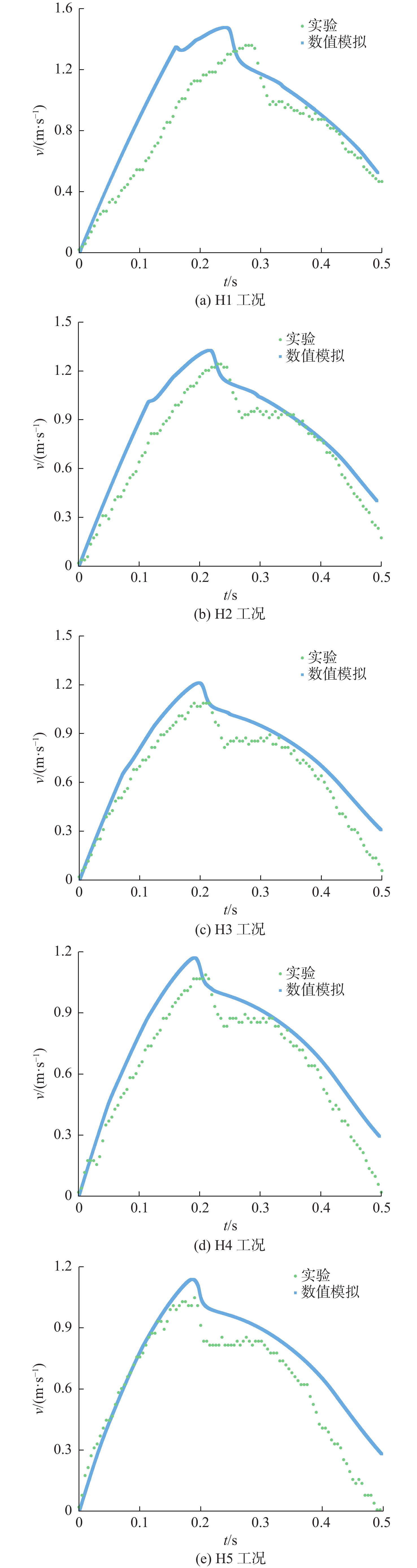
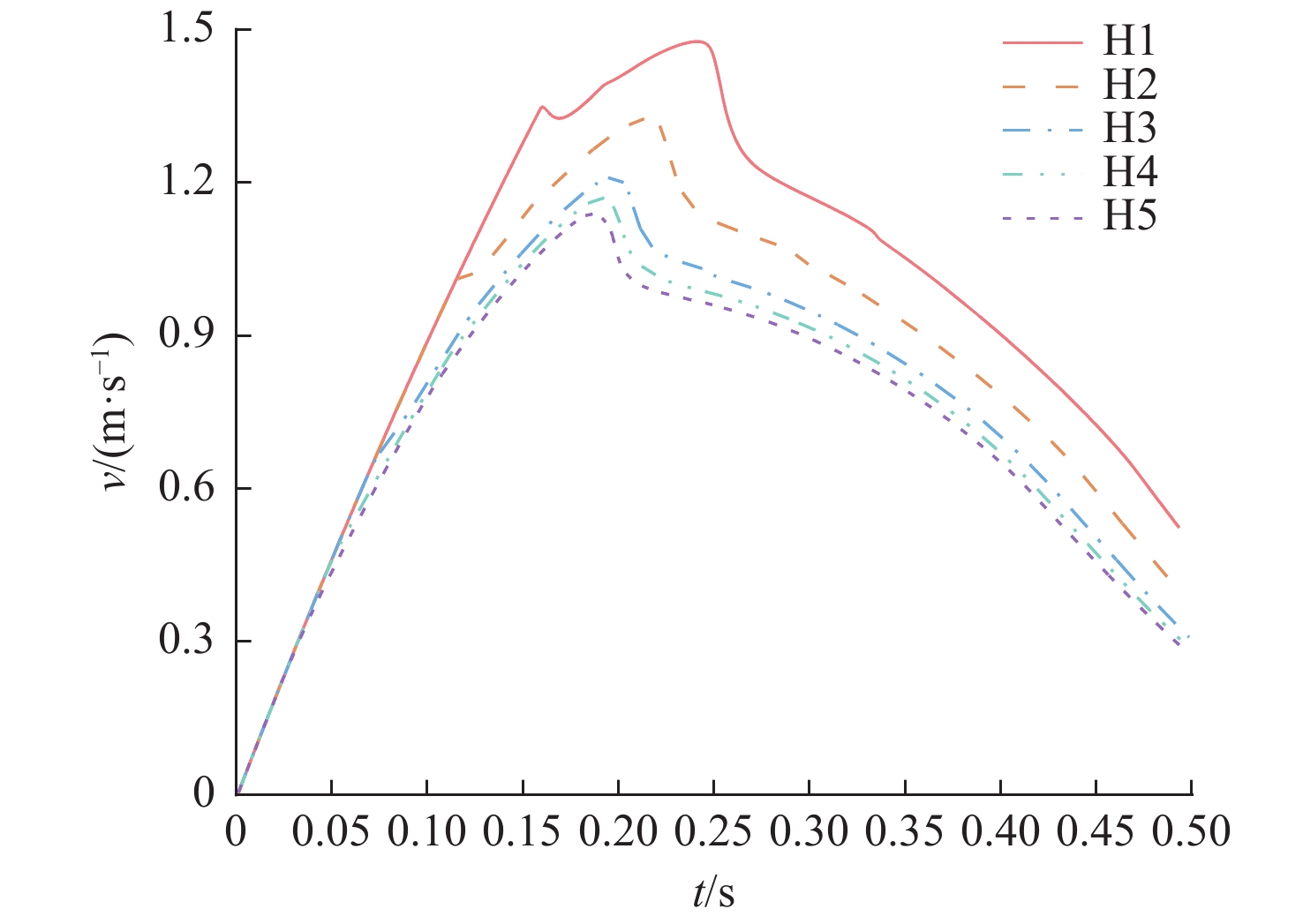
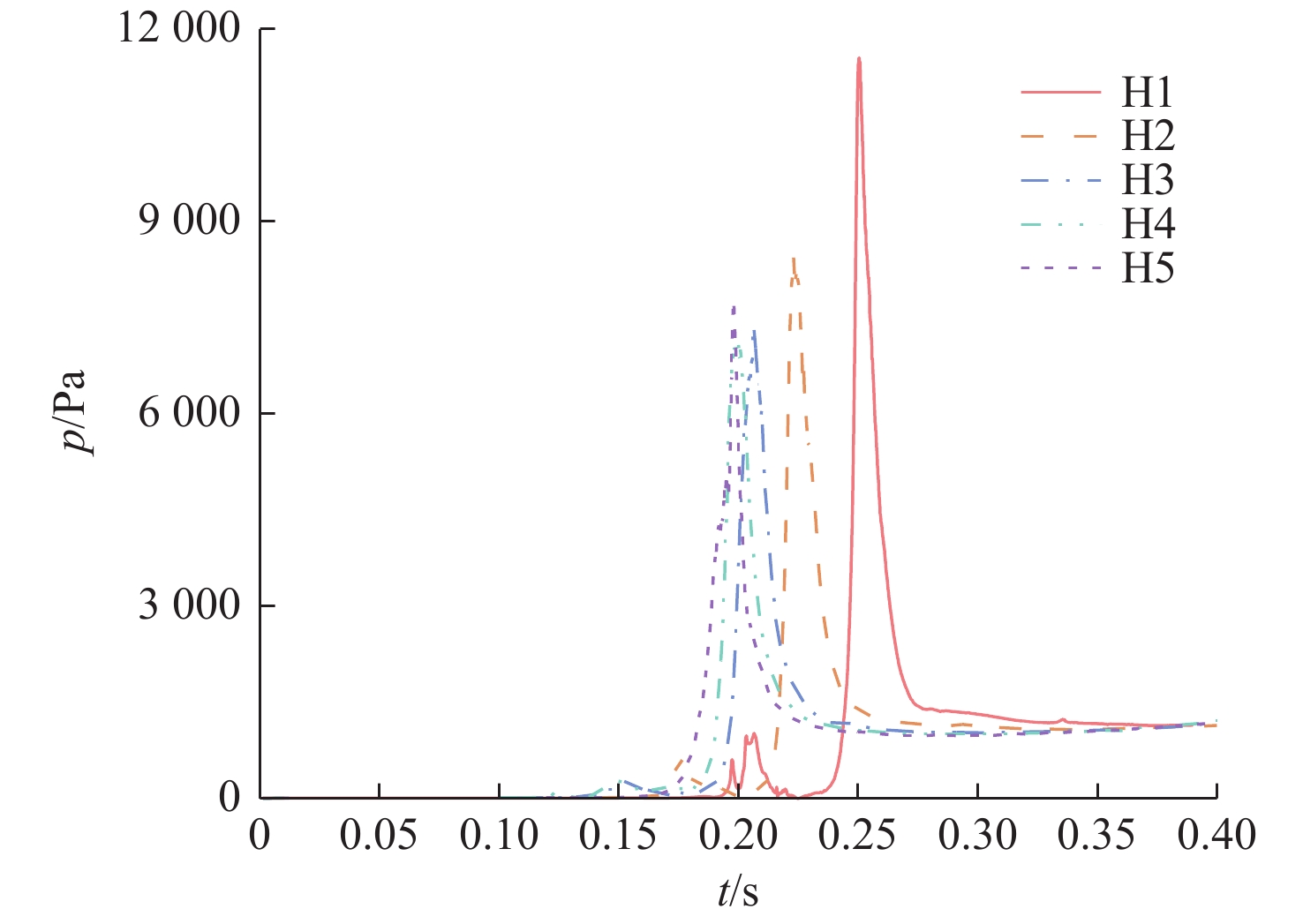
工况 实船入水速度/ (m·s−1) 模型入水速度/ (m·s−1) 落体高度/mm H1 15 1.5 114.8 H2 11 1.1 61.7 H3 7 0.7 25 H4 5 0.5 12.8 H5 3 0.3 4.6 表 2 模型的3种不同网格方案
Table 2 Three different mesh schemes of the model
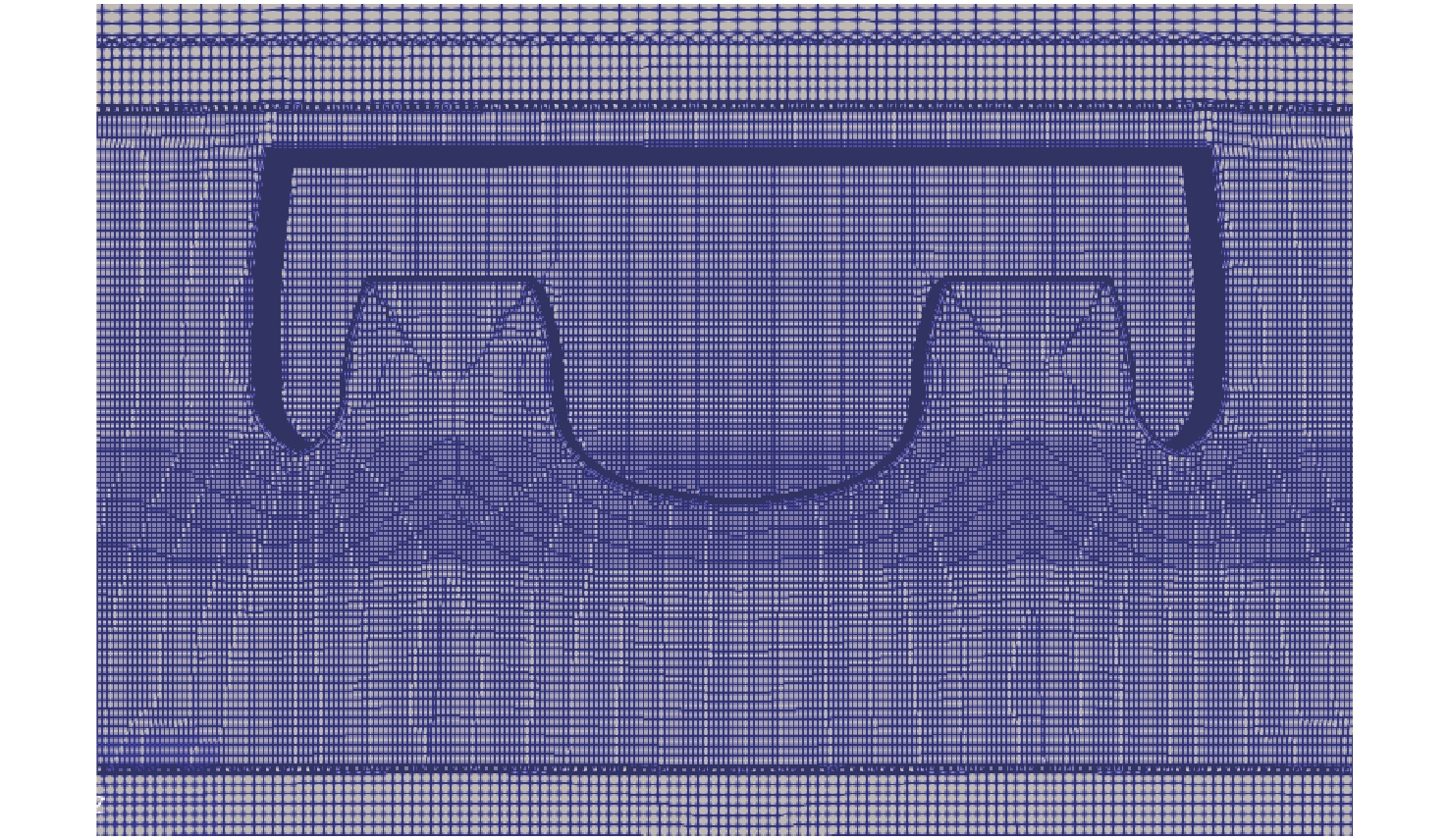
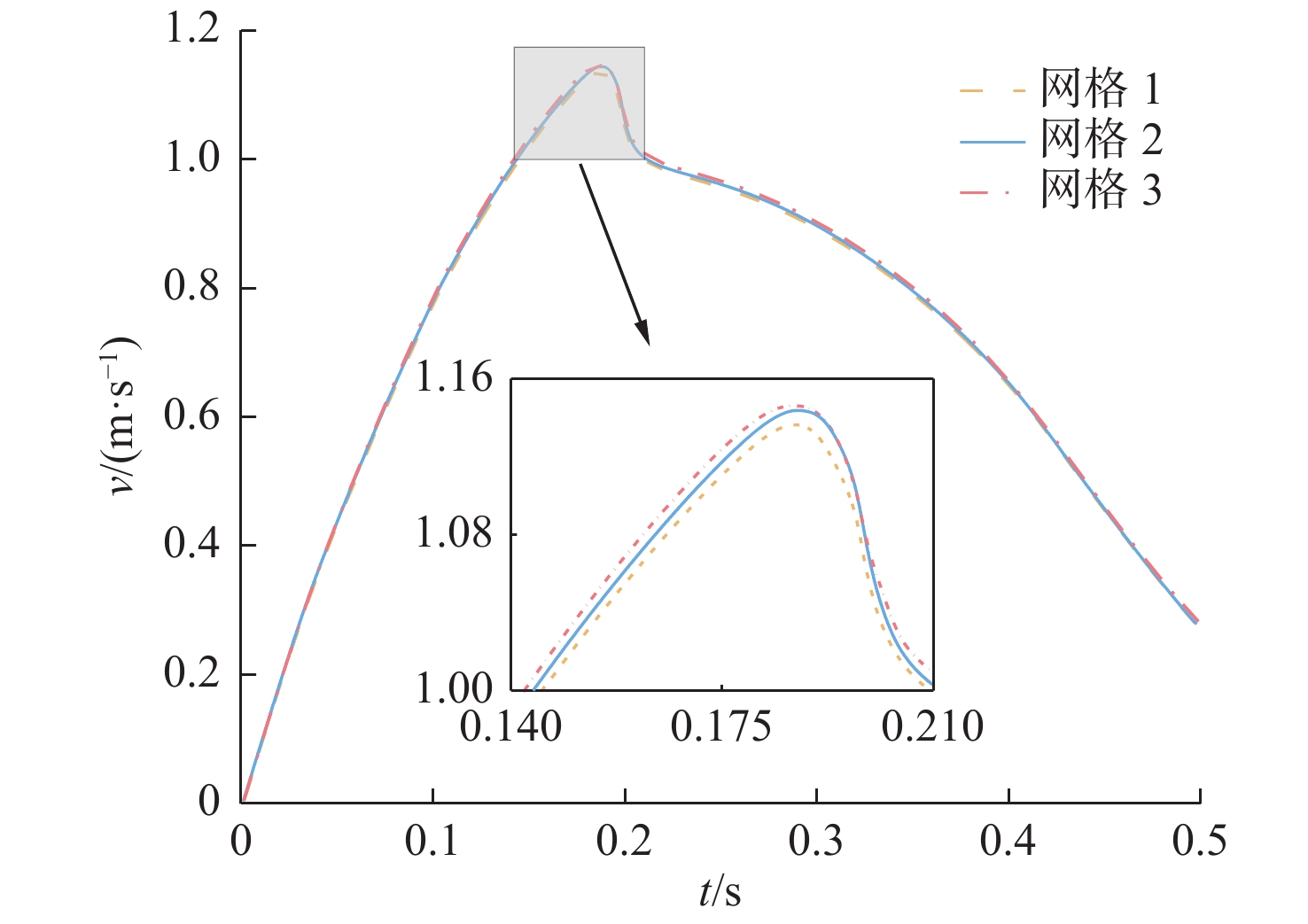
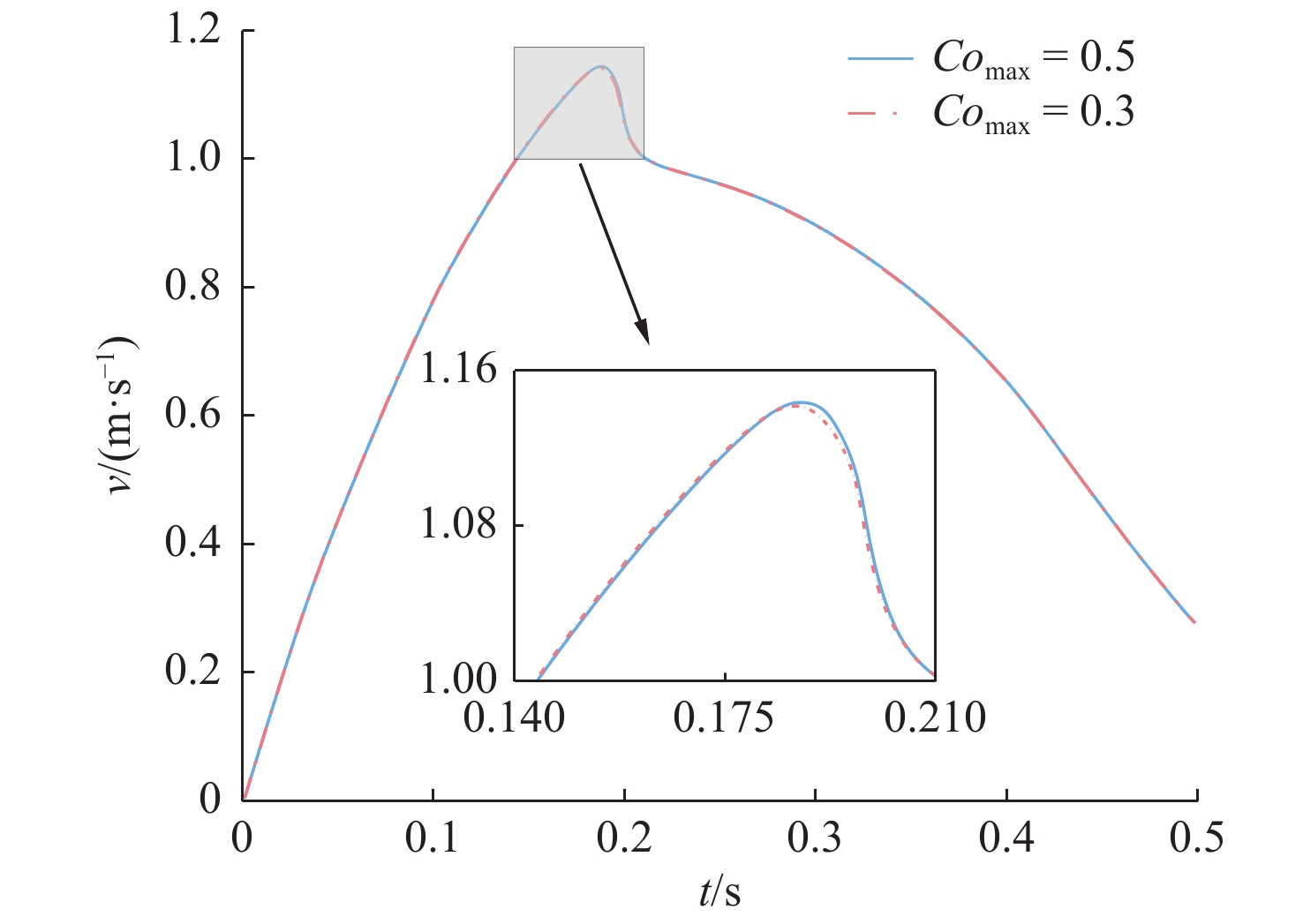
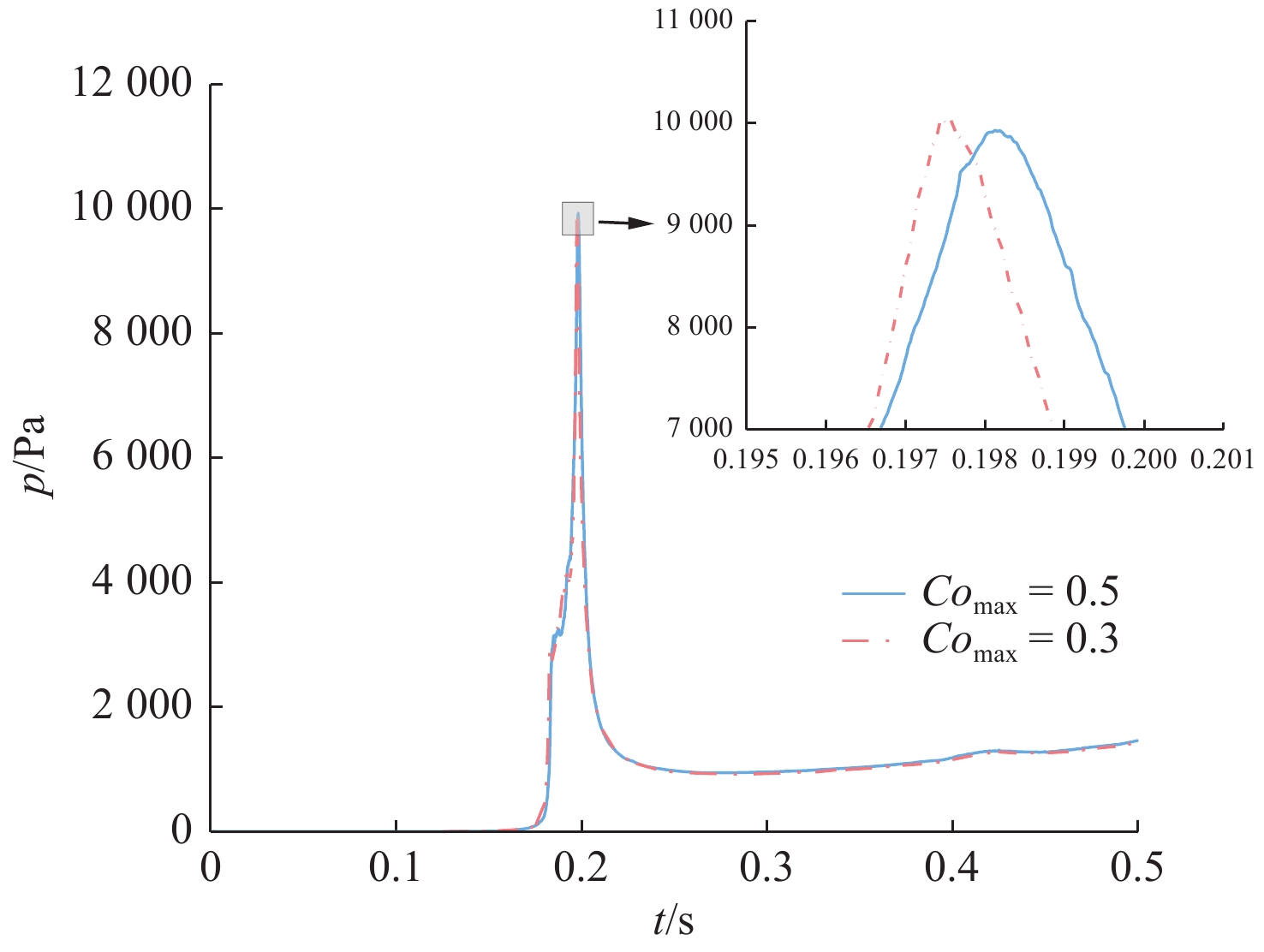
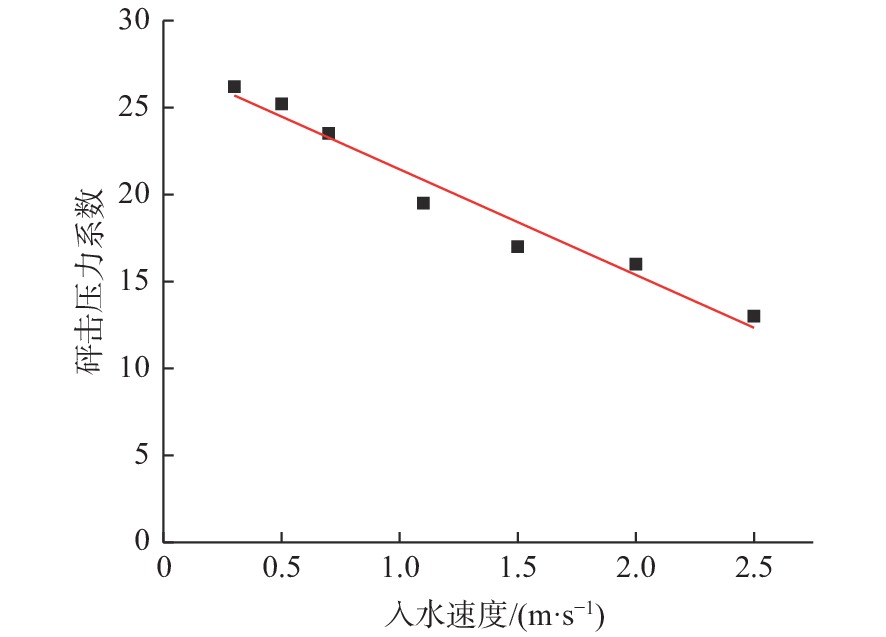
参数 网格1 网格2 网格3 网格数量 3 089 280 3 971 196 5 126177 模型切向最小网格长度/m 0.004 63 0.004 17 0.003 91 模型法向最小网格长度/m 0.004 17 0.004 17 0.004 17 最大库朗数Comax 0.5 0.5, 0.3 0.5 表 3 砰击压力系数与对应的入水速度
Table 3 Slamming pressure coefficient and corresponding water-entry velocities
砰击压力系数 入水速度(m/s) 26.2 0.3 25.2 0.5 23.5 0.7 19.5 1.1 17 1.5 16 2 13 2.5 表 4 角隅压力修正
Table 4 Corner pressure corrections
工况 角隅砰击压力系数 下表面砰击压力系数 比值 H1 17.52 14.76 1.19 H2 22.07 17 1.30 H3 32.34 25.38 1.27 H4 32.75 27.05 1.21 H5 30.93 28 1.10 -
[1] 董传瑞. 三体船连接桥砰击载荷预报方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2018. DONG C R. Research on slamming load forecasting method of trimaran cross-deck[D]. Harbin: Harbin Engineering University, 2018 (in Chinese).
[2] 骆寒冰, 杨宇, 谢芃, 等. 基于OpenFOAM的无转角和有转角楔形体舱段入水砰击载荷数值模拟研究[J]. 船舶力学, 2019, 23(11): 1320–1330. doi: 10.3969/j.issn.1007-7294.2019.11.006 LUO H B, YANG Y, XIE P, et al. Numerical investigation on water impact of one free-drop wedge section considering roll angles using Open FOAM[J]. Journal of Ship Mechanics, 2019, 23(11): 1320–1330 (in Chinese). doi: 10.3969/j.issn.1007-7294.2019.11.006
[3] 卢清亮, 吴梵, 滑林.基于LS-DYAN的穿浪双体船首部入水砰击过程流固耦合动力分析[C]//第十届武汉地区船舶与海洋工程研究生学术论坛论文集. 武汉: [s.n.] 2017: 66–69. LU Q L, WU F, HUA L. Slamming process of wave piercer catamaran based on LS-DYAN dynamic analysis of fluid-structure interaction[M]//Proceedings of the 10th Wuhan Postgraduate Academic Forum on Ship and Ocean Engineering. Wuhan:[s.n], 2017: 66–69 (in Chinese).
[4] 张于维, 王志东, 晋文菊, 等. 二维楔形体砰击载荷研究[J]. 中国舰船研究, 2010, 5(3): 34–37,46. doi: 10.3969/j.issn.1673-3185.2010.03.008 ZHANG Y W, WANG Z D, JIN W J, et al. Numerical simulation on slamming load of two dimensional wedge-shaped section[J]. Chinese Journal of Ship Research, 2010, 5(3): 34–37,46. doi: 10.3969/j.issn.1673-3185.2010.03.008
[5] CHEON J S, JANG B S, YIM K H, et al. A study on slamming pressure on a flat stiffened plate considering fluid–structure interaction[J]. Journal of Marine Science and Technology, 2016, 21(2): 309−324.
[6] HUANG S X, JIAO J L, CHEN C H. CFD prediction of ship seakeeping behavior in bi-directional cross wave compared with in uni-directional regular wave[J]. Applied Ocean Research, 2021, 107: 102426.
[7] ABRAHAMSEN B C, ALSOS H S, AUNE V, E et al. Hydroplastic response of a square plate due to impact on calm water[J]. Physics of Fluids, 2020, 32(8): 082103.
[8] 袁颖聪. 基于CFD的限制水域船体结构入水砰击载荷研究[D]. 广州: 华南理工大学, 2020. YUAN Y C. Numerical investigation of the impact between hull structure and restricted water based on CFD[D]. Guangzhou: South China University of Technology, 2020 (in Chinese).
[9] 方田, 范亚丽, 匡晓峰. 半潜平台波浪砰击数值计算方法研究[M]//吴有生, 王本龙, 俞万能, 等. 第三十一届全国水动力学研讨会论文集(下册). 北京: 海洋出版社, 2020: 974−979. FANG T, FAN Y L, KUANG X F. The numerical of the wave slamming load on semi submersible platform[C]//WU Y S, WANG B L, YU W N, et al. Proceedings of the 31st National Symposium on Hydrodynamics (Volume II). Beijing:China Ocean Press, 2020: 974–979 (in Chinese).
[10] 刘金纯, 马山, 段文洋, 等. 单体剖面垂向自由入水砰击问题模拟研究[M]//吴有生, 王本龙, 何春荣, 等. 第十六届全国水动力学学术会议暨第三十二届全国水动力学研讨会论文集(上册).北京: 海洋出版社, 2021: 125-132. LIU J C, MA S, DUAN W Y, et al. Simulation study on the vertical free water slamming of single section[M]//WU Y S, WANG B L, HE C R, et al. Proceedings of the 16th National Hydrodynamics Academic Conference and the 32nd National Hydrodynamics Symposium (Volume I). Beijing:China Ocean Press, 2021: 125-132(in Chinese).
[11] 李玉君. CFD计算软件OpenFOAM在Wigley船模水动力特性分析的应用[J]. 舰船科学技术, 2020, 42(16): 25–27. LI Y J. Application of CFD calculation software openfoam in hydrodynamic characteristics analysis of Wigley ship model[J]. Ship Science and Technology, 2020, 42(16): 25–27 (in Chinese).
[12] 李裕龙, 朱仁传, 缪国平, 等. 基于OpenFOAM的船舶与液舱流体晃荡在波浪中时域耦合运动的数值模拟[J]. 船舶力学, 2012, 16(7): 750–758. doi: 10.3969/j.issn.1007-7294.2012.07.004 LI Y L, ZHU R C, MIAO G P, et al. Simulation of ship motions coupled with tank sloshing in time domain based on Open FOAM[J]. Journal of Ship Mechanics, 2012, 16(7): 750–758 (in Chinese). doi: 10.3969/j.issn.1007-7294.2012.07.004
[13] 谢路毅, 张晓嵩, 万德成. 基于重叠网格方法模拟物体入水[M]//吴有生, 邵雪明, 王军, 等. 第三十届全国水动力学研讨会暨第十五届全国水动力学学术会议论文集(上册).北京: 海洋出版社, 2019: 702–710. XIE L Y, ZHANG X S, WAN D C. Numerical simulation of water entry of cylinder and box square column based on overset grid method[M]//WU Y S, SHAO X M, WANG J, et al.Proceedings of the 30th National Hydrodynamics Symposium and the 15th National Hydrodynamics Academic Conference (Volume I) .Beijing: China Ocean Press, 2019: 702–710 (in Chinese).
[14] 姜帆, 李云波, 闫凤超, 等. 基于OpenFOAM的非对称双体船操纵性预报及运动特性研究[J]. 中国造船, 2021, 62(2): 14–24. doi: 10.3969/j.issn.1000-4882.2021.02.002 JIANG F, LI Y B, YAN F C, et al. Prediction and characteristics of maneuvering performance for asymmetric catamaran based on OpenFOAM[J]. Shipbuilding of China, 2021, 62(2): 14–24 (in Chinese). doi: 10.3969/j.issn.1000-4882.2021.02.002
[15] WANG K, MA X, BAI W, et al. Numerical simulation of water entry of a symmetric/asymmetric wedge into waves using OpenFOAM[J]. Ocean Engineering, 2021, 227: 108923.
[16] XIANG G, WANG S,SOARES C G. Study on the motion of a freely falling horizontal cylinder into water using OpenFOAM[J]. Ocean Engineering, 2020, 196: 106811.
[17] MA Z H, QIAN L. Numerical simulation of wave slamming on wedges and ship sections during water entry[J]. Ocean Systems Engineering, 2018, 8(2):183−199
[18] KATSIDONIOTAKI E, GÖTEMAN M. Numerical modeling of extreme wave interaction with point-absorber using OpenFOAM[J]. Ocean Engineering, 2022, 245: 110268.
[19] TANG S Q, ZHANG Y, SUN S L, et al. Experimental investigation on the air-cushion effect during free fall of a trimaran section using an air escape control method[J]. Ocean Engineering, 2022, 254: 111417.




 下载:
下载: