短路冲击下的船用柴油机瞬态扭振特性分析

徐聪聪; 梁刚; 陶杰; 焦亚飞; 陈晋元; 王鹏程; 邓梦灿

doi:10.19693/j.issn.1673-3185.03409

短路冲击下的船用柴油机瞬态扭振特性分析

1.
上海船用柴油机研究所，上海 201108
2.
哈尔滨工程大学动力与能源工程学院，黑龙江哈尔滨 150001

详细信息

作者简介:
徐聪聪，女，1985年生，硕士，高级工程师

梁刚，男，1977年生，博士，研究员

陶杰，男，1997年生，博士生

通讯作者:
徐聪聪

中图分类号: U664.21；U664.121
计量
- 文章访问数: 227
- HTML全文浏览量: 32
- PDF下载量: 13
出版历程
- 收稿日期: 2023-06-12
- 修回日期: 2023-08-04
- 网络出版日期: 2023-08-07

Transient torsional vibration analysis of marine diesel engine under short-circuit impact

1.
Shanghai Marine Diesel Engine Research Institute, Shanghai 201108, China
2.
College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China

短路冲击下的船用柴油机瞬态扭振特性分析徐聪聪，采用知识共享署名4.0国际许可协议进行许可。

摘要

摘要:
目的为提出船用柴油发电机组的轴系扭振参数优化方案，需分析其在短路冲击下的瞬态扭转振动特性。
方法采用Newmark法，以某型20 V柴油发电机组的短路冲击工况为例，对比不同轴系参数对轴系瞬态扭振特性的影响规律，进而基于参数优化结果来确定新的机组减振器刚度与联轴器刚度选配方案。
结果研究结果表明：发生短路冲击时，轴系扭振特性将显著恶化；经优化之后（将扭振减振器刚度、联轴器刚度分别优选为原始值的90%和70%），短路冲击工况下的电机轴瞬时最大附加应力、联轴器瞬时最大扭矩、曲轴各轴段瞬时最大应力分别降低了13.43%，10.51%，5.29%。
结论该参数优化方案可以有效降低轴系的瞬态扭振水平，研究成果可为柴油发电机组的减振降噪设计提供参考。
- 船用柴油机 /
- 轴系扭振 /
- 短路冲击 /
- 参数优化
Abstract:
Objectives In order to formulate an optimization plan for the torsional vibration parameters of a marine diesel generator shaft system, it is necessary to analyze the transient torsional vibration characteristics of the diesel generator under short-circuit impact.
Methods The shafting transient torsional vibration character-istics of a 20-cylinder V-type diesel generator set under short-circuit impact are analyzed by the Newmark method, and the effects of different shafting parameters on its shafting transient torsional vibration characteristics under short-circuit conditions are discussed. A new selection scheme of shock absorber stiffness and coupling stiffness is then determined.
Results The calculation results show that the shafting torsional vibration characteristics deteriorate significantly when short-circuit impact occurs. After optimization (the stiffness of the torsional shock absorber and coupling are optimized to 90% and 70% of the original value respectively), the instantaneous maximum torque of the motor shaft, instantaneous maximum torque of the coupling and instantaneous maximum stress of each shaft section of the crankshaft under short-circuit impact conditions are reduced by 13.43%, 10.51% and 5.29% respectively.
Conclusions The proposed optimized design scheme can effectively reduce the transient torsional vibration level of shafting systems. The results of this study can provide useful references for the vibration and noise reduction design of diesel generator sets.
- marine diesel /
- shafting torsional vibration /
- short-circuit shock /
- parameter optimization

HTML全文

0. 引　言

柴油发电机组是重要的能源转换设备，常被作为驱动电源、备用电源和应急电源等长期性或过渡性供电设备而广泛应用于核电、船舶等领域。在船舶柴油发电机组的设计制造中，扭振考核作为其船检的必检项目之一，各大船级社均对柴油发电机组的扭振计算与评估提出了相应要求。在传统的扭振计算中，主要关注由柴油机激励引起的扭转振动，而忽视了发电机激励的激振作用，且主要聚焦于稳态响应，对动态过程中瞬态扭振特性的关注尚存不足。然而，当柴油发电机组出现短路故障时，发电机转矩将产生数倍于额定转矩的大幅振荡，故其对轴系扭振的激励作用不容忽视。因此，为避免短路产生的巨大激励力矩对机组造成破坏，有必要对船用柴油发电机组在短路冲击下的瞬态扭振特性分析方法进行研究，进而提出切实可行的柴油发电机组轴系扭振参数优化方案，以减小短路冲击对柴油发电机组安全性的不利影响。

目前，针对柴油机轴系扭振的研究已较为普遍，马怀腾等^[1]针对大功率柴油机长轴系的特性，采用加装惯量盘的方法使扭振固有频率的低谐次避开工作转速区，成功消除了机组的运行安全隐患。Liu等^[2]提出了一种基于柴油发电机组柔性联轴器的扭转振动，用以开展发动机失火诊断，并进行了仿真与试验结果对比。董焕彬等^[3]提出了通过优化轴系关键参数来解决匹配大刚度联轴器引起的轴系共振问题。胡云波^[4]通过建立一套含凸轮轴系、正时齿轮系的柴油发电机组多分支轴系扭振模型，对某柴油发电机组异常声响问题进行了研究。Kim等^[5]研究了涡轮增压器切断系统对柴油机扭振特性的影响。Mirošević等^[6]建立了由柴油机、同步发电机和电机驱动组成的整体电机传动数学模型，分析了发电机组和感应电动机在冲击载荷下的动态特性。

目前，在短路冲击下的轴系瞬态振动特性研究方面，国内外学者在汽轮发电机组、柴油发电机组、电力推进系统等领域都开展了大量研究工作。向玲等^[7]采用逐步积分法对汽轮发电机在短路工况和非同期并网工况下的轴系扭转振动进行了计算，结果表明，短路冲击将激起轴系的多阶扭振固有频率，从而加剧轴系扭振。何成兵等^[8]利用增量传递矩阵法对汽轮发电机组在出口端短路故障下的弯扭耦合振动特性进行了分析，发现短路冲击对机组轴系弯振与扭振均存在显著的影响。李晓茜等^[9]采用逐步积分法和系统矩阵法对柴油发电机组正常工况下和两相短路工况下的轴系扭转振动进行了计算，结果表明，发生短路故障时，考虑发电机激振力的计算结果更符合实际情况。李增光等^[10]对短路工况下电力推进轴系的扭转振动响应进行了优化，结果表明，在轴系中增加弹性联轴器可以降低轴系扭转振动的幅值。由此可见，短路激励对轴系扭振特性的影响不容忽视，通过优化轴系关键部件的参数，即可改善轴系振动响应水平。

需注意的是，设备短路故障的发生存在不定时性，短路冲击出现时刻也不尽相同，短路冲击激励与正常工况下轴系扭振激励之间的叠加相位也有所不同。如果忽略短路冲击激励与正常工况下扭振激励的相位匹配关系，则将导致轴系振动响应分析结果存在偏差，而上述研究成果中均未体现激励叠加相位对轴系扭振特性的影响。

为此，本文拟以某型20 V船用柴油发电机组轴系为研究对象，综合考虑柴油机激励、短路冲击激励对轴系扭振的激振作用并将重点关注两者之间的相位匹配关系，通过采用Newmark法对机组轴系在短路冲击下的瞬态扭振特性开展研究，并分析减振器、联轴器、电机转子等关键部件参数对瞬态扭振特性的影响规律，进而提出轴系参数优化方案。

1. 轴系当量模型与激励分析

1.1 柴油发电机组轴系当量模型

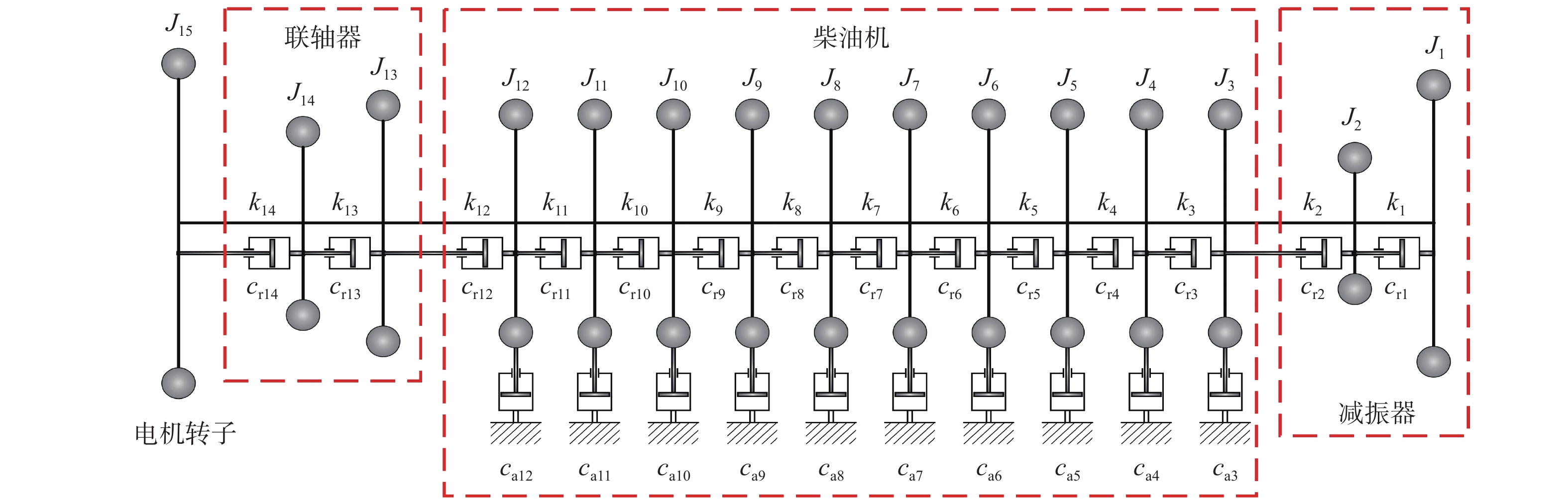
本文的研究对象为某型20 V船用柴油发电机组轴系系统，其由1台20缸V列柴油机、弹性联轴器和1台交流发电机组成。采用集总参数法建立相应的轴系扭振当量模型，机组扭振系统由15个惯性质量和相邻2个惯量之间的14个扭转刚度组成，其中：惯量1，2为减振器惯量；惯量3～12为曲轴惯量；13号和14号分别为联轴器的主动端和从动端；15号惯量为发电机转子惯量。轴系扭转振动微分方程如式（1）所示，具体模型如图1所示。

图 1 柴油机组轴系的当量模型

Figure 1. The equivalent system of diesel shafting

下载: 全尺寸图片幻灯片

$\left[ {\boldsymbol{J}} \right]\left\{ {\ddot \varphi } \right\} + \left[ {\boldsymbol{C}} \right]\left\{ {\dot \varphi } \right\} + \left[ {\boldsymbol{K}} \right]\left\{ \varphi \right\} = \left\{ {\boldsymbol{M}} \right\}$

(1)

式中： $\left[ {\boldsymbol{J}} \right]$ ， $\left[ {\boldsymbol{C}} \right]$ ， $\left[ {\boldsymbol{K}} \right]$ 分别为轴系惯量矩阵、阻尼矩阵和刚度矩阵； $\left\{ {\ddot \varphi } \right\}$ ， $\left\{ {\dot \varphi } \right\}$ ， $\left\{ \varphi \right\}$ 分别为轴系扭振角加速度、角速度、角位移； $\left\{ {\boldsymbol{M}} \right\}$ 为轴系扭振激振力矩向量。

惯量矩阵 $\left[ {\boldsymbol{J}} \right]$ 为对角矩阵，基于矩阵元素J₁～J₁₅，其表达式为

$\left[ {\boldsymbol{J}} \right] = \left[ {\begin{array}{*{20}{c}} {{J_1}}&{}&{}&{}&{} \\ {}&{{J_2}}&{}&{}&{} \\ {}&{} &\ddots &{}&{} \\ {}&{}&{}&{{J_{14}}}&{} \\ {}&{}&{}&{}&{{J_{15}}} \end{array} } \right]$

(2)

刚度矩阵 $\left[ {\boldsymbol{K}} \right]$ 为三对角矩阵，基于矩阵元素k₁～k₁₄，其表达式为

$\left[ {\boldsymbol{K}} \right] = \left[ {\begin{array}{*{20}{c}} {{k_1}}&{ - {k_1}}&{}&{}&{} \\ { - {k_1}}&{{k_1} + {k_2}}&{ - {k_2}}&{}&{} \\ {}&{ - {k_2}}& \ddots & \ddots &{} \\ {}&{}& \ddots &{{k_{13}} + {k_{14}}}&{ - {k_{14}}} \\ {}&{}&{}&{ - {k_{14}}}&{{k_{14}}} \end{array}} \right]$

(3)

阻尼矩阵 $\left[ {\boldsymbol{C}} \right] = \left[ {{{\boldsymbol{C}}_{\text{a}}}} \right] + \left[ {{{\boldsymbol{C}}_{\text{r}}}} \right]$ ，其中绝对阻尼矩阵 $\left[ {{{\boldsymbol{C}}_{\text{a}}}} \right]$ 和相对阻尼矩阵 $\left[ {{{\boldsymbol{C}}_{\text{r}}}} \right]$ 的形式分别与惯量矩阵 $\left[ {\boldsymbol{J}} \right]$ 和刚度矩阵 $\left[ {\boldsymbol{K}} \right]$ 相同，矩阵元素分别由相对阻尼c_r1～c_r14和绝对阻尼c_a1～c_a15组成，其中减振器与联轴器绝对阻尼为0，交流发电机组绝对阻尼较小予以忽略，故图1仅需考虑柴油机气缸的绝对阻尼c_a3～c_a12。

1.2 柴油机轴系扭振激励分析

1.2.1 柴油机气缸激励形成

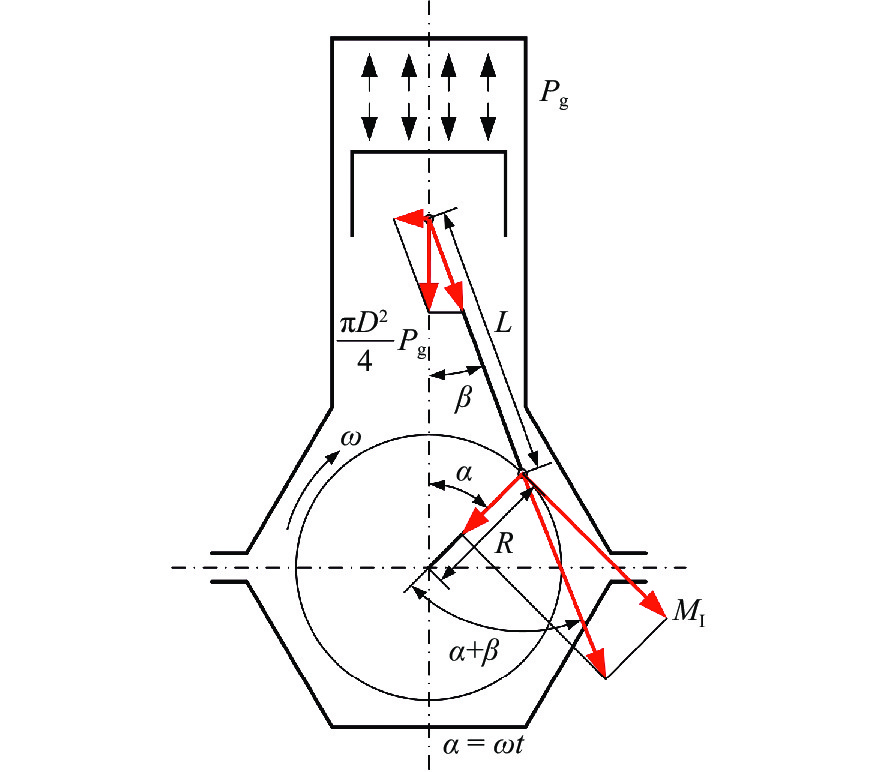
在柴油机扭振分析中，一般主要考虑气体压力变化产生的激励力矩与运动部件惯性力产生的激振力矩的激振作用，柴油机动力学原理如图2所示。

图 2 柴油机动力学示意图

Figure 2. Schematic diagram of the diesel engine-kinematic

下载: 全尺寸图片幻灯片

首先，估算气体压力变化产生的激励力矩。由可知，作用在曲柄上的切向力 ${P_{\text{τ }}}$ 为

${P_{\text{τ }}} = {P_{\text{g}}}{{\sin (\alpha + \beta )} \mathord{\left/ {\vphantom {{\sin (\alpha + \beta )} {\cos \beta }}} \right. } {\cos \beta }}$

(4)

式中： ${P_{\text{τ }}}$ 为切向力； ${P_{\text{g}}}$ 为活塞单位面积的气体压力； $\alpha$ 为曲轴转角； $\beta$ 为连杆摆角。

将式（4）均以 $\alpha$ 角形式简化，则可近似为

${P_{\text{τ }}} = \left[ {\sin \alpha + \left( {{R \mathord{\left/ {\vphantom {R {2L}}} \right. } {2L}}} \right)\sin 2\alpha } \right]{P_{\text{g}}}$

(5)

式中：R为曲柄半径；L为连杆长度。

因此，可以采用切向力 ${P_{\text{τ }}}$ 对曲轴产生的扭矩来表示气体压力变化产生的激励力矩M_g：

${M_{\text{g}}} = \left( {{{{\text{π}}{D^2}} \mathord{\left/ {\vphantom {{{\text{π}}{D^2}} 4}} \right. } 4}} \right)R{P_{\text{τ }}}$

(6)

式中，D为气缸直径。

由式（6）可知，柴油机气体压力激振力矩变化规律与切向力 ${P_{\text{τ }}}$ 的变化规律完全一致，因此，对气体压力激振力矩进行简谐分析即为对切向力进行简谐分析。

由数学分析可知，切向力 ${P_{\text{τ }}}$ 的傅里叶级数展开形式为

${P_{\text{τ }}} = {a_0} + \sum\limits_{v{\text{ = }}1}^\infty {({a_v}} \cos v\omega t + {b_v}\sin v\omega t)$

(7)

式中： ${a_0}$ 为平均切向力；v为简谐次数，其中v= 1, 2, …, ∞； ${a_v}$ ， ${b_v}$ 分别为v谐次简谐切向力的正弦分量和余弦分量； $\omega$ 为曲轴角速度，其中t为时间。

则柴油机气体压力激振力矩M_g的分谐次展开形式为

${M_{\text{g}}} = \left( {{{{\text{π}}{D^2}} \mathord{\left/ {\vphantom {{{\text{π}}{D^2}} 4}} \right. } 4}} \right)R\sum\limits_{v{\text{ = }}1}^\infty {({a_v}} \cos v\omega t + {b_v}\sin v\omega t)$

(8)

然后，估算运动部件的惯性力：

${P_{\text{I}}} = -m\ddot x$

(9)

式中： ${P_{\text{I}}}$ 为往复运动件产生的往复惯性力；m为往复质量； $\ddot x$ 为活塞加速度。

根据内燃机运动学，活塞加速度的近似公式为

$\ddot x = R{\omega ^2}(\cos \alpha + \lambda \cos 2\alpha ) \times {10^{ - 2}}$

(10)

式中， $\lambda$ 为曲柄连杆比。

则往复惯性力可表示为

${P_{\text{I}}} = - mR{\omega ^2}(\cos \alpha + \lambda \cos 2\alpha ) \times {10^{ - 2}}$

(11)

往复惯性力产生的激振力矩M_I为

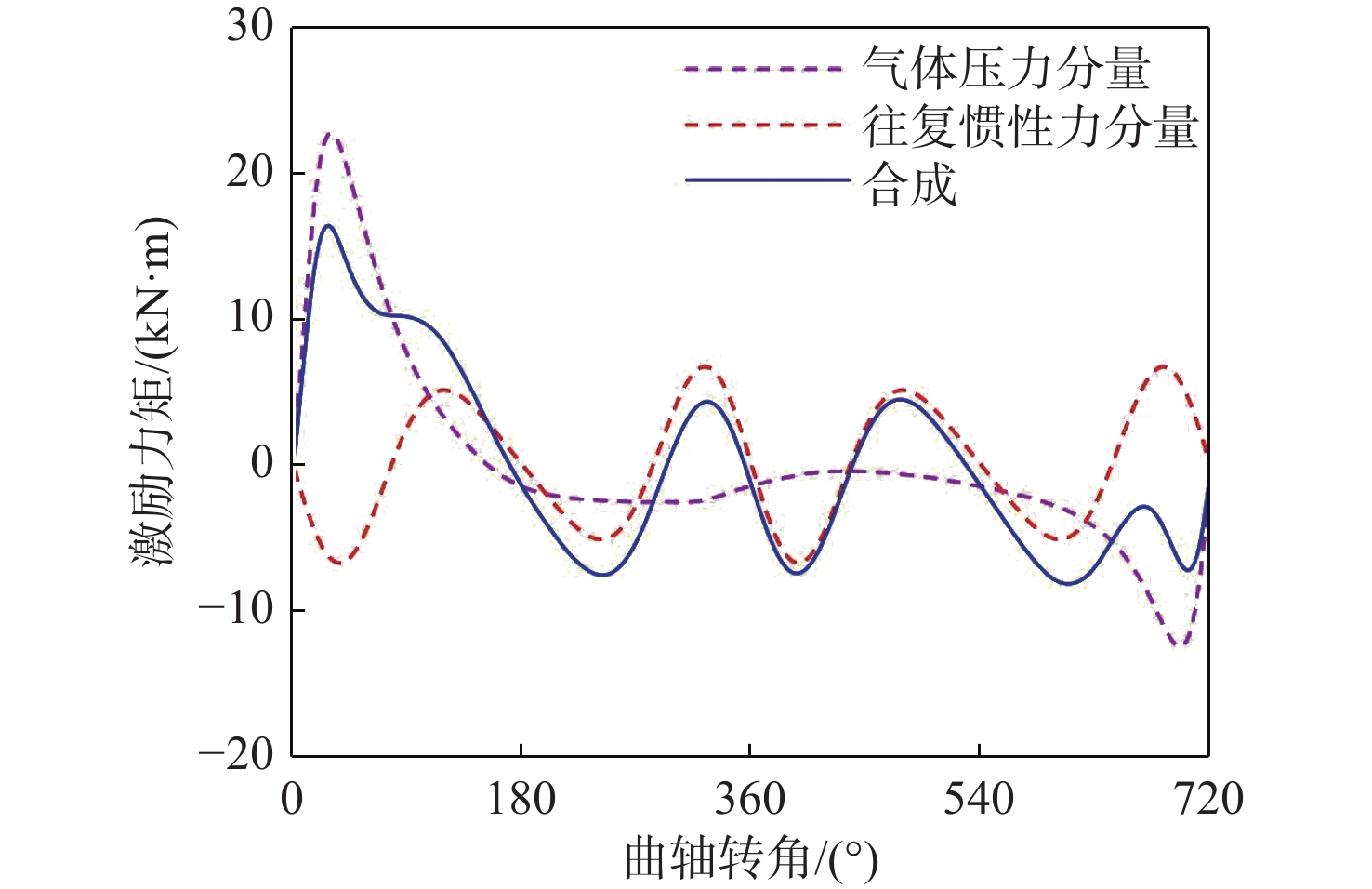
$\begin{gathered} {M_{\text{I}}} = {P_{\text{I}}}R\left( {{{\sin (\alpha + \beta )} / {\cos \beta }}} \right) \approx \\ - m{R^2}{\omega ^2}(\cos \alpha + \lambda \cos 2\alpha )(\sin \alpha + \,\,({\lambda /2})\sin 2\alpha ){\text{ = }} \\ - m{R^2}{\omega ^2}[ ({\lambda / 4})\sin \alpha - ({1 / 2})\sin 2\alpha - \\ ({{3\lambda } / 4})\sin 3\alpha - ({{{\lambda ^2}} / 4})\sin 4\alpha ] \end{gathered}$

(12)

最终，计算柴油机轴系扭振时，须同时考虑气体压力和往复惯性力影响下的计算分析需求，将两者按式（13）进行谐次合成，即可得到柴油机轴系扭振激励，其中气体压力激励一般考虑至12谐次。柴油机气缸激励的合成结果如图3所示。

图 3 柴油机的气缸激励合成

Figure 3. Cylinder excitation of diesel engine

下载: 全尺寸图片幻灯片

${M_{\text{k}}} = {M_{\text{g}}} + {M_{\text{I}}}$

(13)

式中， ${M_{\text{k}}}$ 为柴油机的扭振激励力矩。

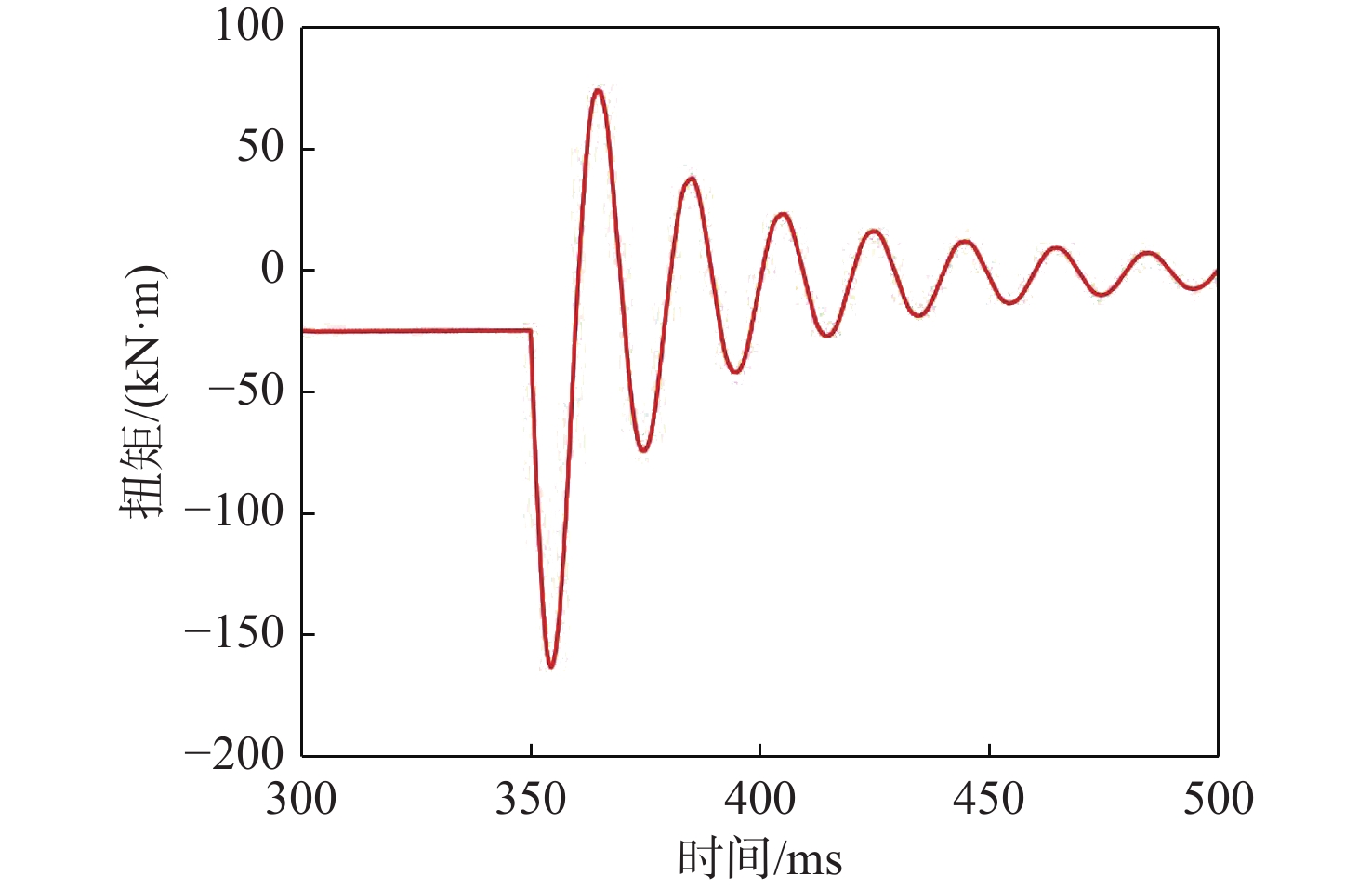
1.2.2 短路冲击激励

发电机发生三相短路冲击故障时产生的短路冲击扭矩（作用于发电机惯量）由发电机厂家提供，其时域结果如图4所示。

图 4 发电机的短路冲击力矩

Figure 4. Impact torque of generator under short-circuit faults

下载: 全尺寸图片幻灯片

2. 轴系扭振特性分析

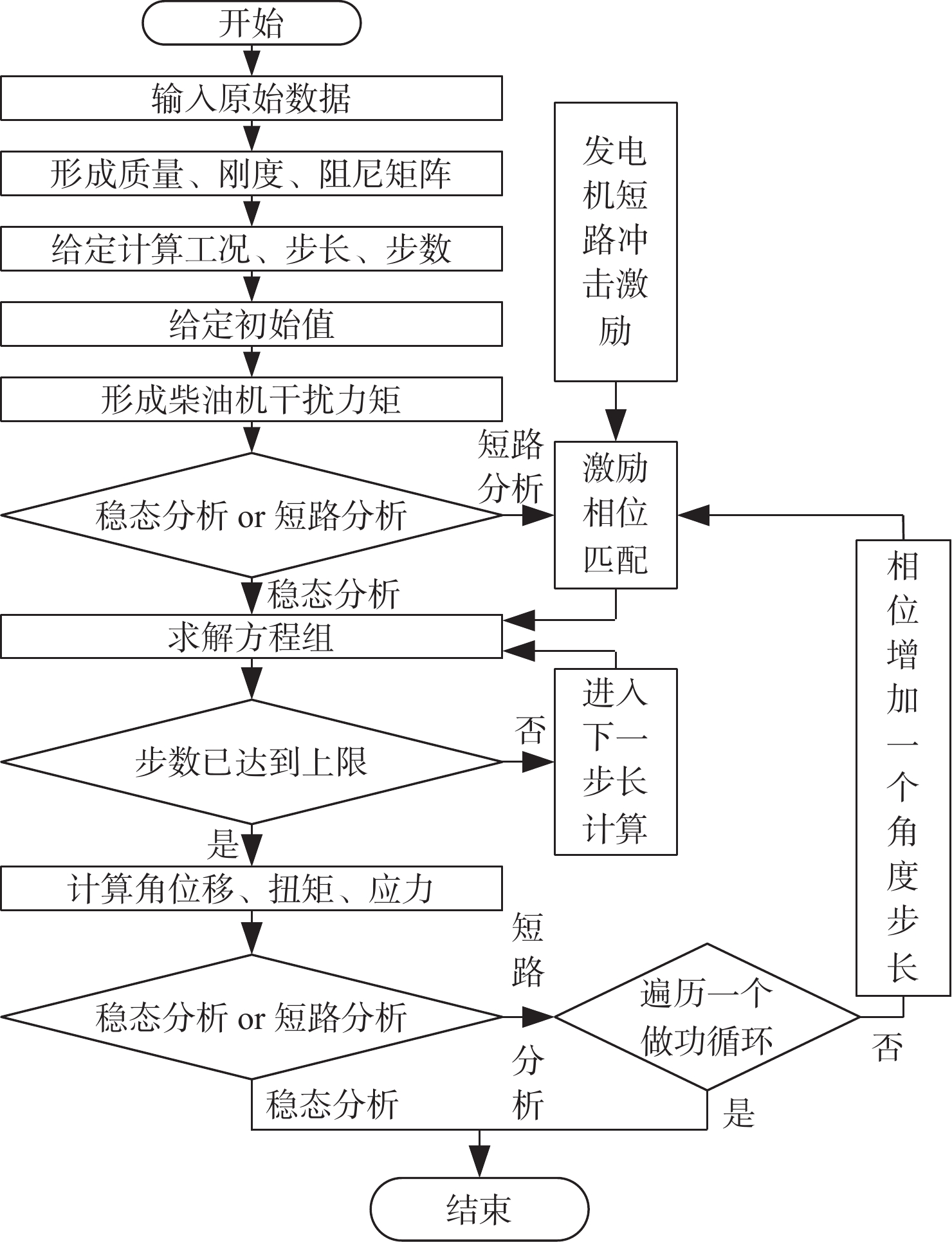
本文将采用时域法中的Newmark法^[11]计算柴油发电机组的稳态、瞬态振动响应，Newmark法作为线性加速度法的推广，属于逐步积分法，是时域响应求解的常用方法之一。研究表明，当 $\beta \geqslant {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}$ 且 $\alpha \geqslant {1 \mathord{\left/ {\vphantom {1 4}} \right. } 4}{\left( {\beta + {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}} \right)^2}$ ，Newmark法均可无条件稳定，但在使用时需注意 $\alpha$ ， $\beta$ 这2个参数的选取，计算流程如图5所示。

图 5 强迫振动响应的计算流程图

Figure 5. Calculation process of forced vibration response

下载: 全尺寸图片幻灯片

需注意的是，在短路冲击下的柴油发电机组瞬态扭振特性分析中，由于发电机组短路冲击发生的随机性，需对柴油机一个做功循环内（二冲程机为360°、四冲程机为720°）任意相位处发生短路冲击的工况进行分析，从而得到轴系扭振响应最为恶劣的短路冲击作用相位。

2.1 正常工况下轴系扭振计算

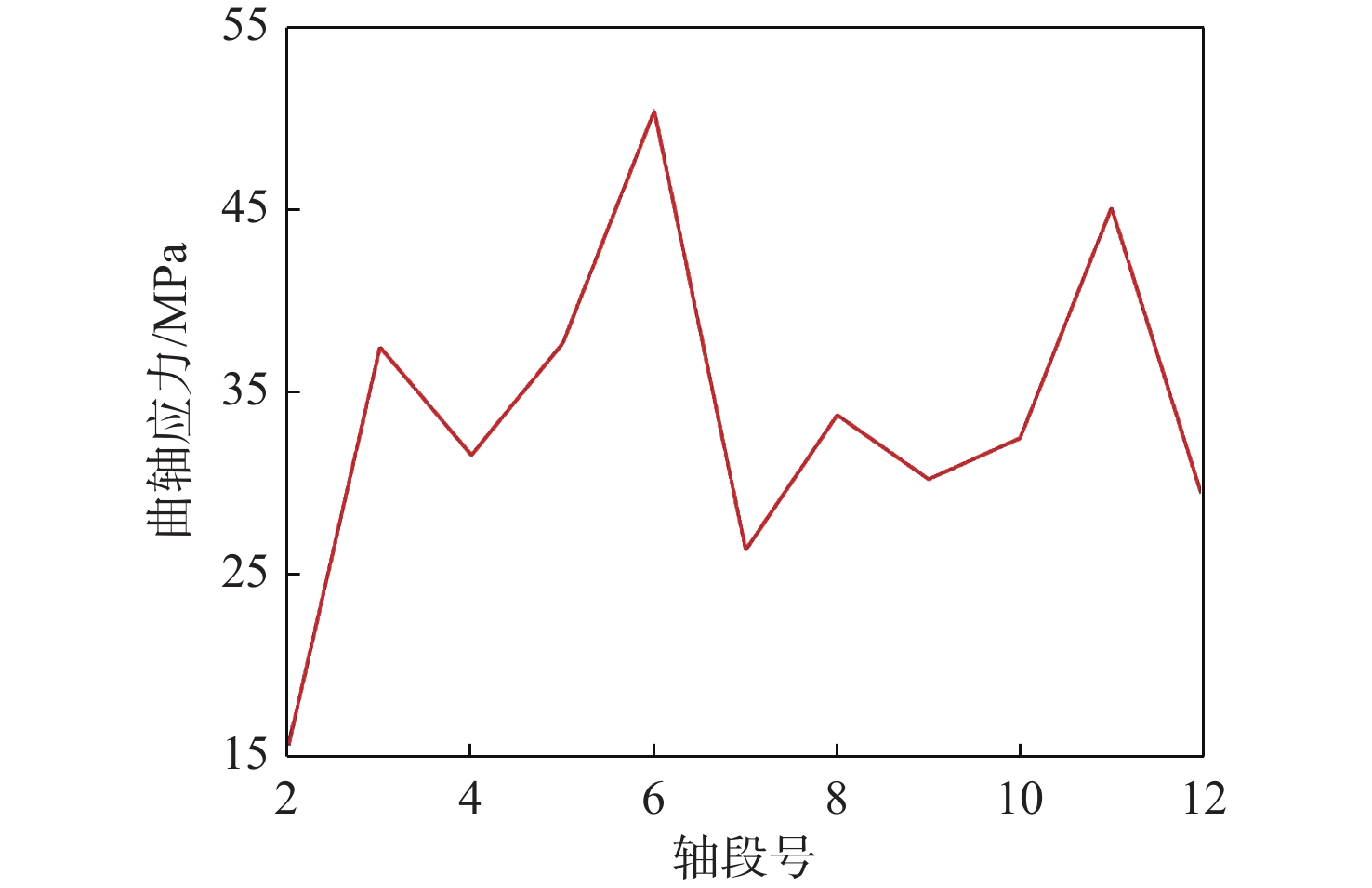
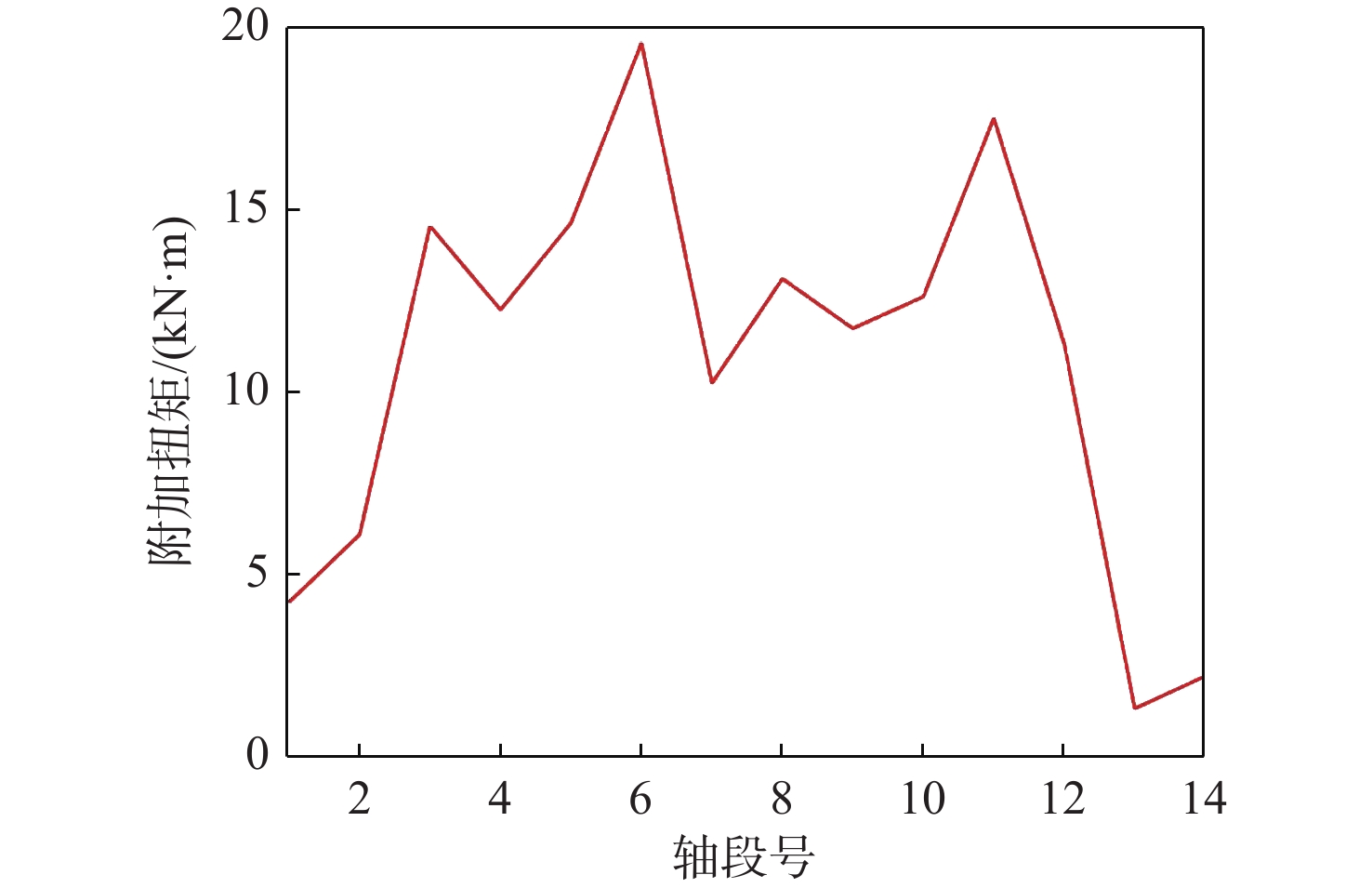
不考虑短路冲击对轴系扭振的影响，仅考虑上文形成的柴油机气缸激励，即可得到如图6和图7所示的柴油发电机组轴系扭振计算结果，分别为曲轴各轴段的最大稳态附加应力（最大值50.49 MPa）、轴系各轴段的稳态附加扭矩（最大值19.55 kN·m）。

图 6 曲轴各轴段的最大应力

Figure 6. Maximum torsional stress of crankshaft

下载: 全尺寸图片幻灯片

图 7 各轴段的附加扭矩

Figure 7. Additional torque of shafting

下载: 全尺寸图片幻灯片

2.2 短路工况下轴系扭振计算

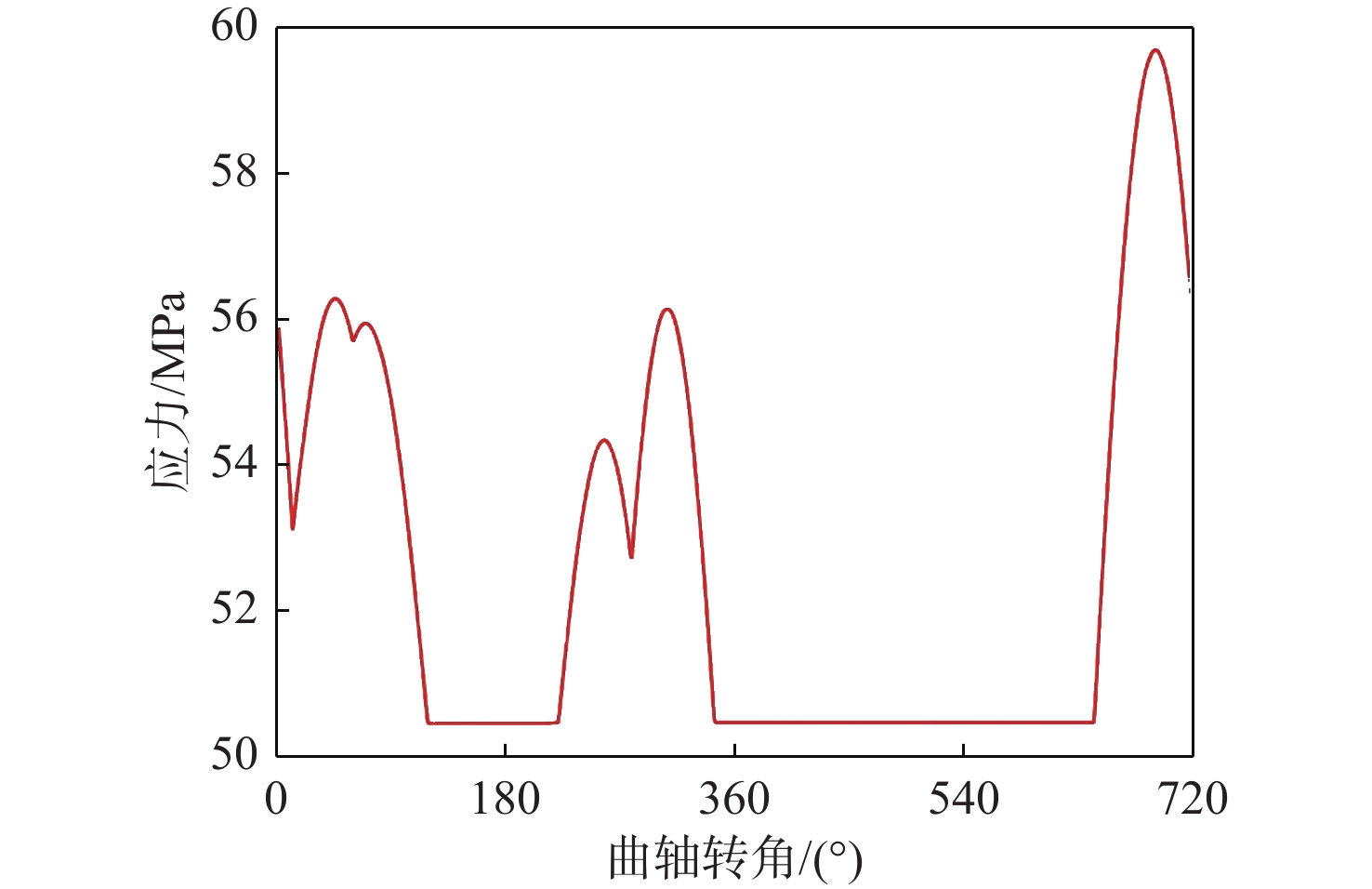
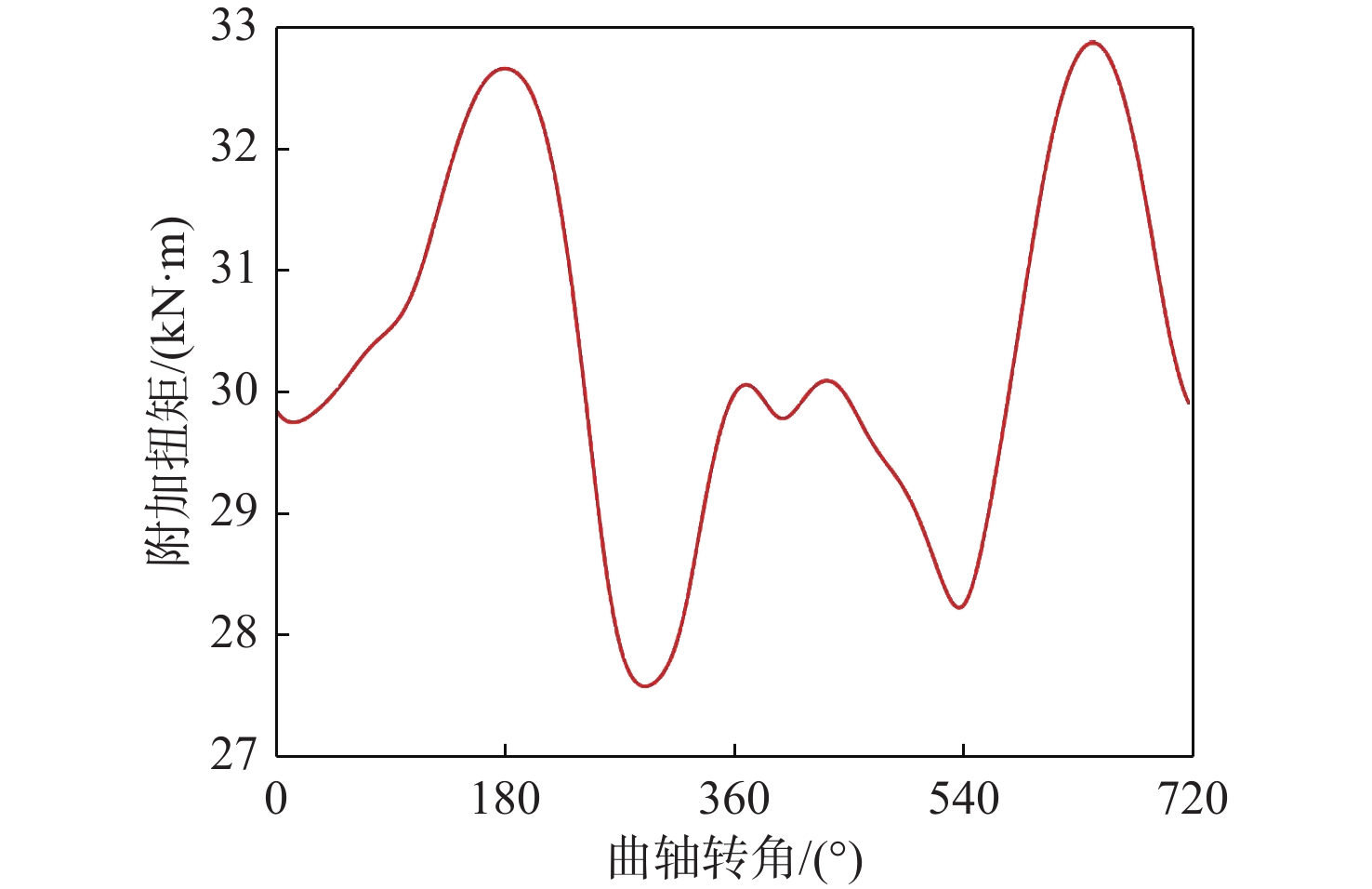
综合考虑柴油机激励和短路激励时，由于激励相位叠加的影响以及出现短路故障的不定时性，因此计算了在柴油机一个周期（720°）内不同时刻加入短路冲击的情况，结果如图8～图10所示，可以看出在不同的激励叠加相位下，柴油发电机组的轴系扭振响应存在显著差异。

图 8 不同冲击加入时刻下，曲轴轴段的瞬时最大应力

Figure 8. Instantaneous maximum torsional stress of crankshaft under different impact times

下载: 全尺寸图片幻灯片

图 9 不同冲击加入时刻下，联轴器的瞬时最大附加扭矩

Figure 9. Instantaneous maximum vibration torque of coupling under different impact times

下载: 全尺寸图片幻灯片

图 10 不同冲击加入时刻下，电机输入轴的瞬时附加应力

Figure 10. Instantaneous torsional stress of generator rotor under different impact times

下载: 全尺寸图片幻灯片

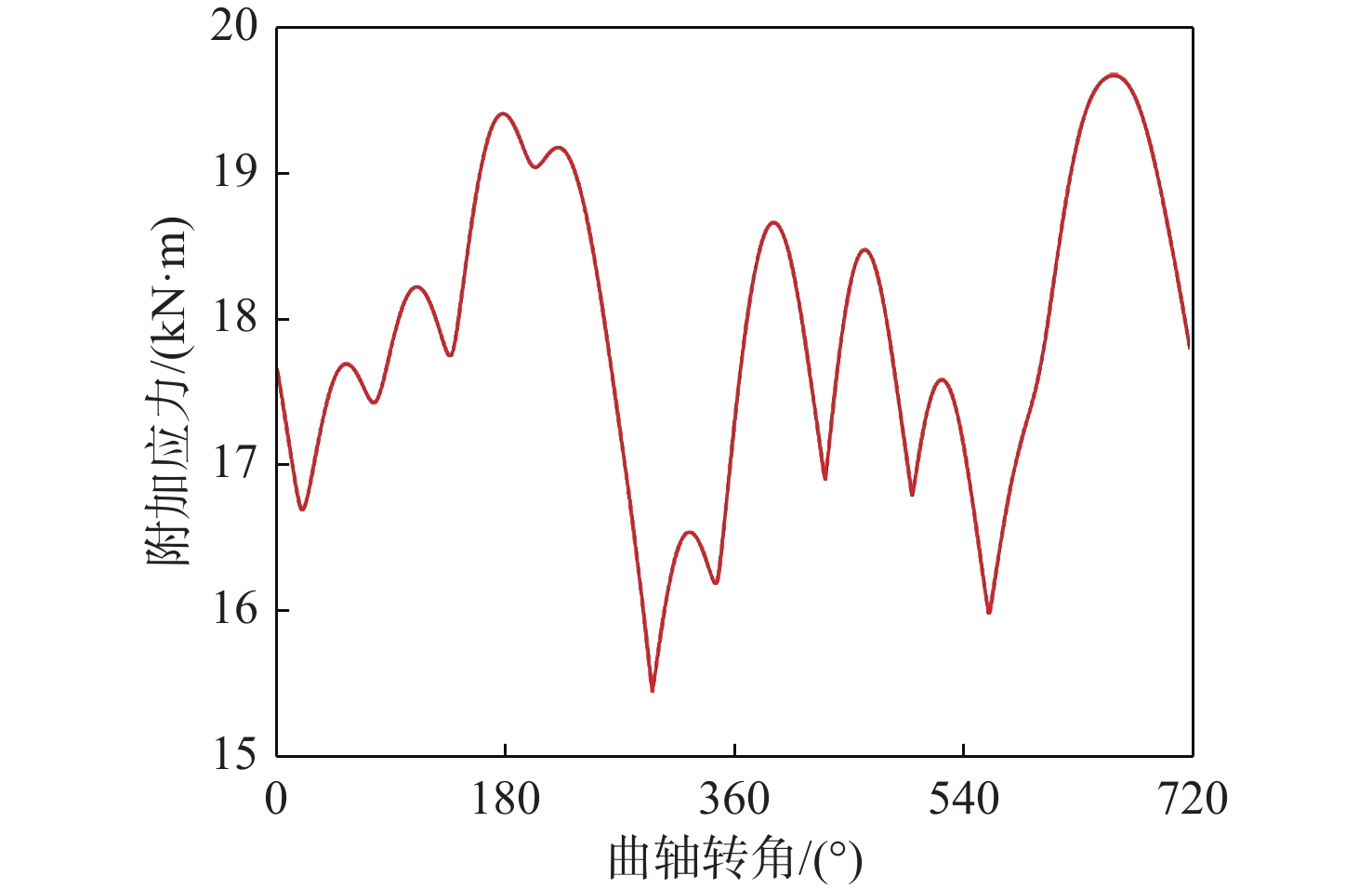
由图8可知，当冲击扭矩施加在曲轴转角119°～214°范围内时，曲轴轴段的最大瞬态扭振应力为50.49 MPa；当施加相位为345°～643°时，最大应力略有增加，可达50.50 MPa；当施加相位为691°时，最大应力则达到了59.72 MPa，即最大值与最小值相差9.23 MPa。由图9可知，当冲击扭矩施加在曲轴转角290°与642°时，弹性联轴器的最大瞬时附加扭矩分别达到最小值27.60 kN·m与最大值32.88 kN·m，两者相差5.28 kN·m。由图10则可以看出，当冲击扭矩施加在曲轴转角296°与658°时，电机输入轴的最大瞬时附加应力分别达到最小值15.46 MPa与最大值19.68 MPa，两者相差4.02 MPa。

3. 考虑短路冲击影响的轴系参数优化

本节将在冲击扭矩施加于曲轴转角691°时，即出现曲轴轴段最大瞬时附加应力的相位下，研究联轴器刚度、扭振减振器刚度和电机转子惯量对轴系瞬时扭振特性的影响规律，其中轴系原始参数如表1所示。

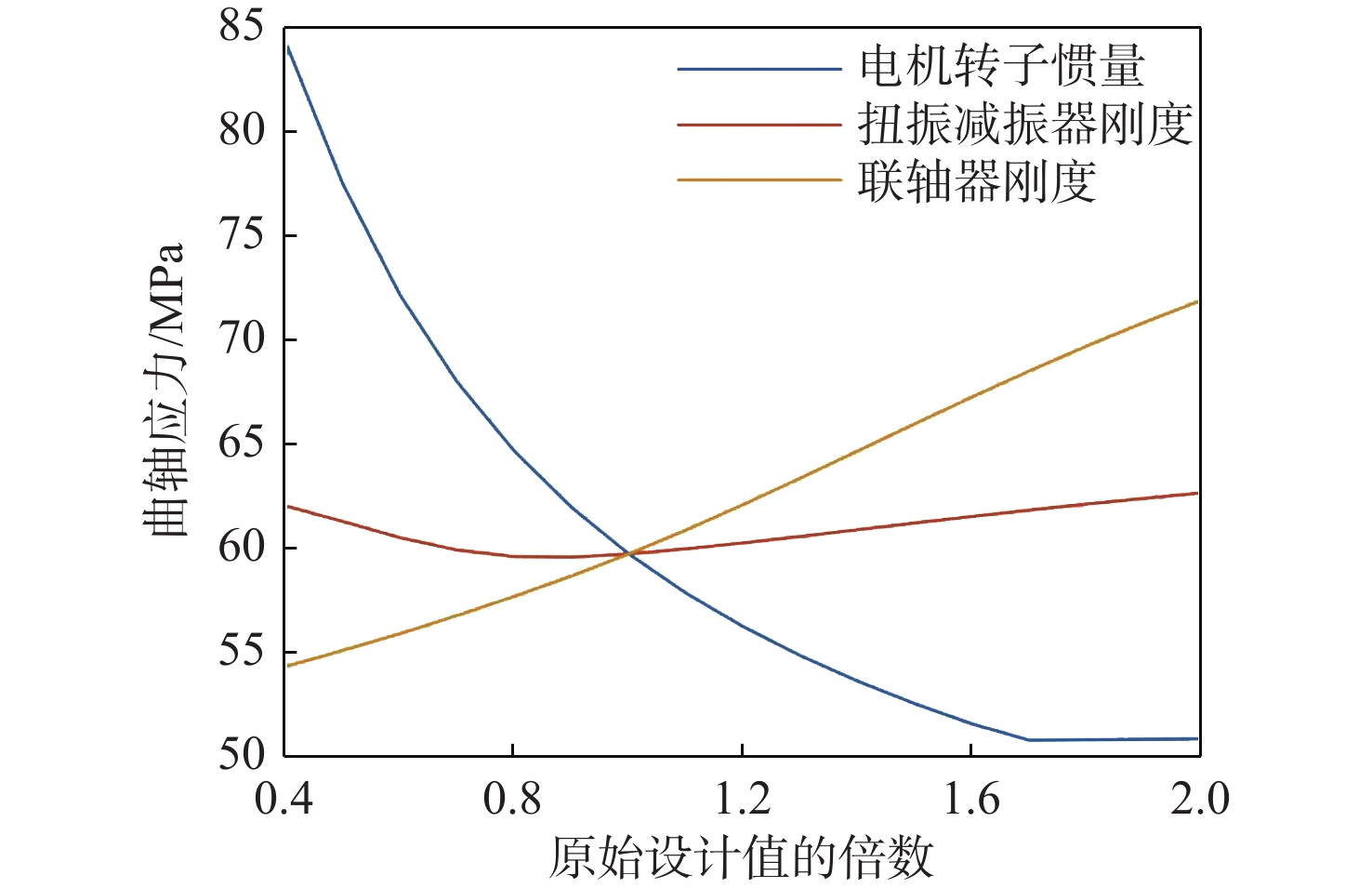
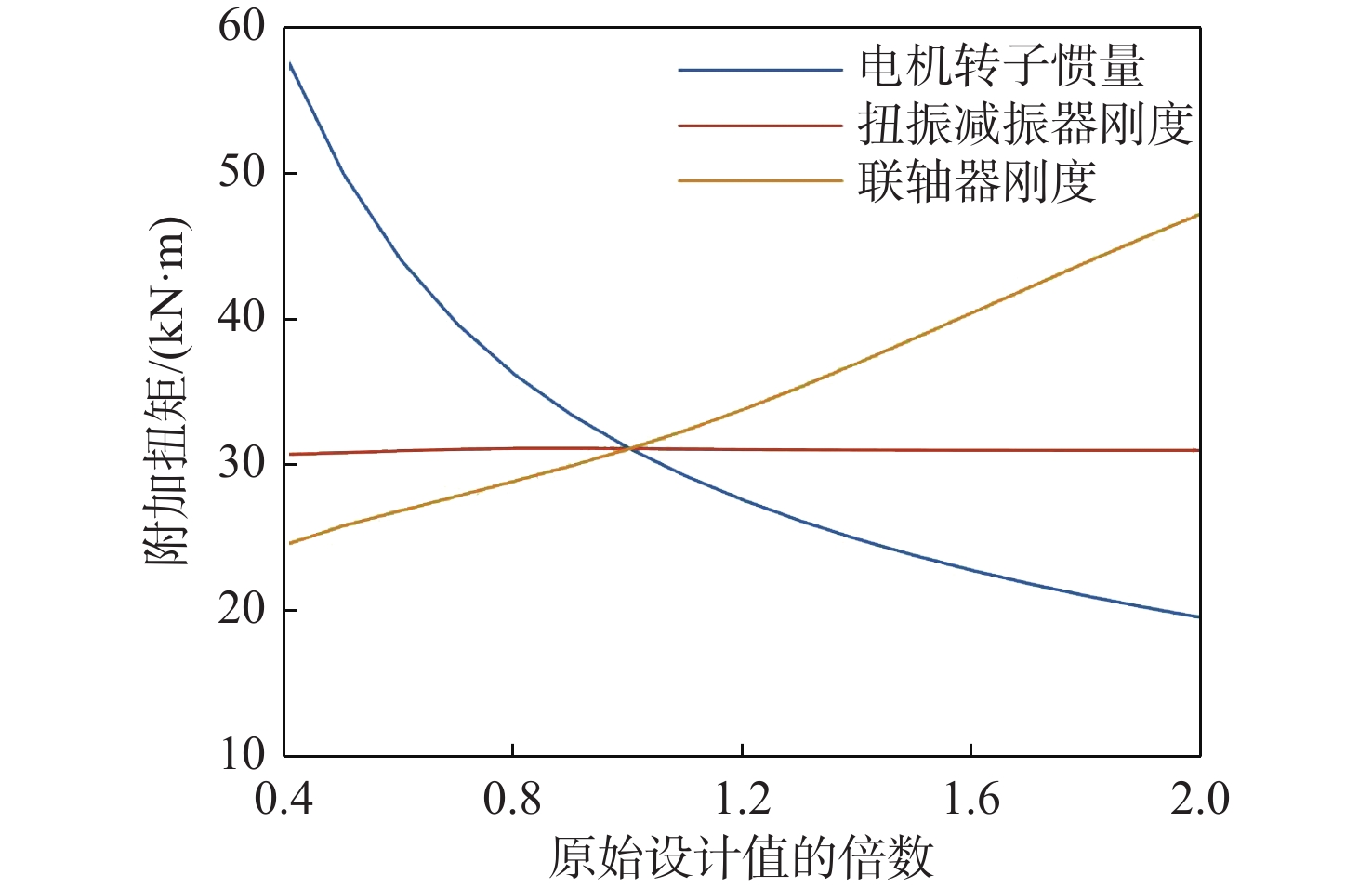
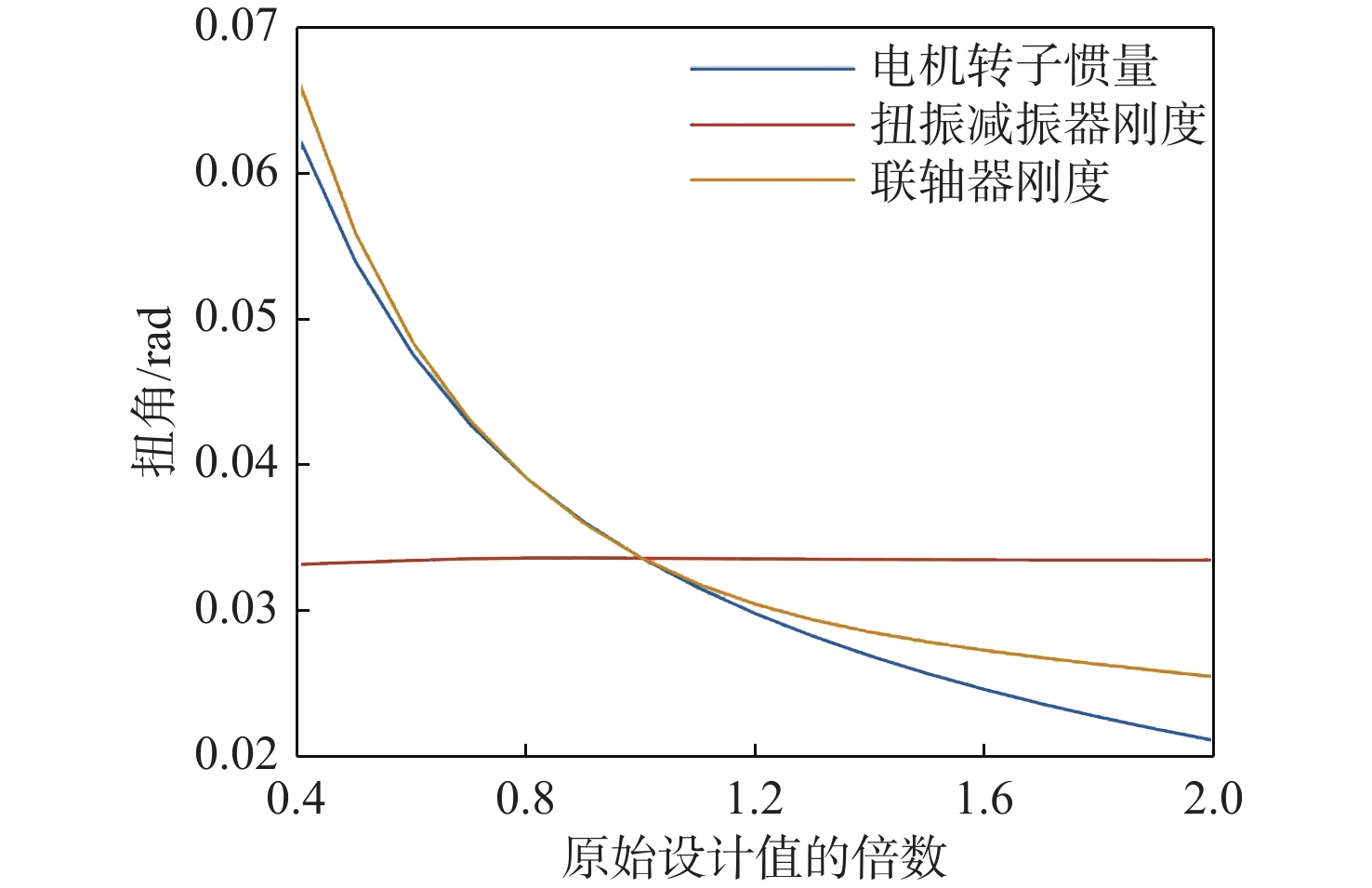
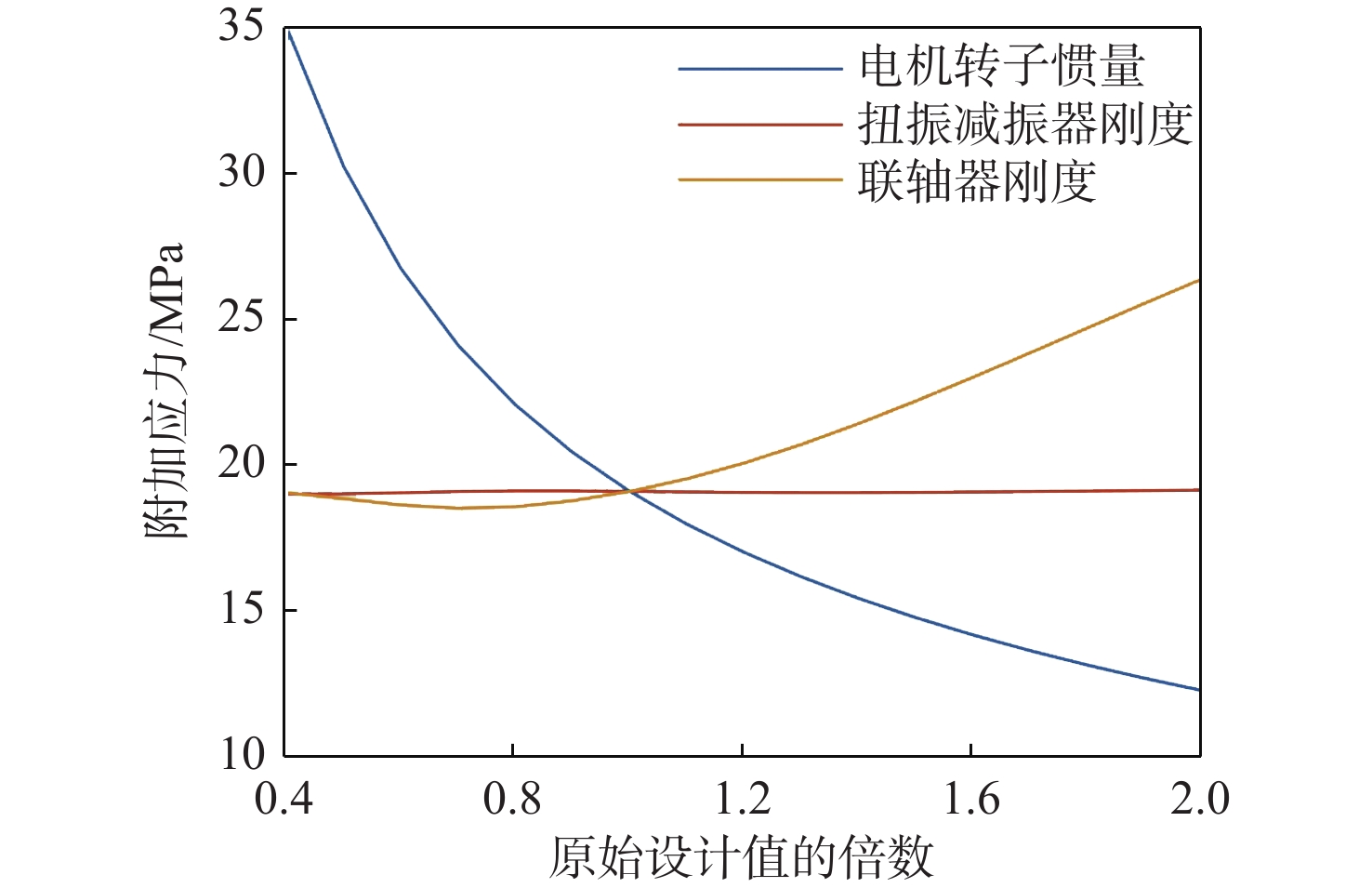
表 1 轴系原始参数值

Table 1. Original parameters of shafting

参数	数值
联轴器刚度/(N·m·rad⁻¹)	0.927 E+06
减振器刚度/(N·m·rad⁻¹)	1.37 E+06
发电机转子惯量/(kg·m²)	200

下载: 导出CSV

| 显示表格

将联轴器刚度、扭振减振器刚度和电机转子惯量的参数值分别设定为原始值的0.4～2倍，分析其对曲轴瞬时最大应力、联轴器瞬时最大附加扭矩、联轴器瞬时最大相对角位移、电机轴瞬时最大附加应力的影响，结果如图11～图14所示。根据分析结果，扭振减振器刚度对联轴器后端轴系的扭振特性影响较小，取0.9倍原始设计刚度值时，曲轴各轴段的瞬时最大应力最小；随着电机惯量的增加，轴系扭振水平将显著降低；随着联轴器刚度的增加，曲轴瞬时最大应力和联轴器扭矩也将随之增加，当联轴器刚度为原始值的0.7倍时，电机轴瞬时最大应力将出现最小值。

图 11 曲轴的瞬时最大应力

Figure 11. Instantaneous maximum stress of crankshaft

下载: 全尺寸图片幻灯片

图 12 联轴器的瞬时最大附加扭矩

Figure 12. Instantaneous maximum additional torque of coupling

下载: 全尺寸图片幻灯片

图 13 联轴器的瞬时最大相对角位移

Figure 13. Instantaneous maximum relative angular displacement of coupling

下载: 全尺寸图片幻灯片

图 14 电机轴的瞬时最大附加应力

Figure 14. Instantaneous torsional stress of generator rotor

下载: 全尺寸图片幻灯片

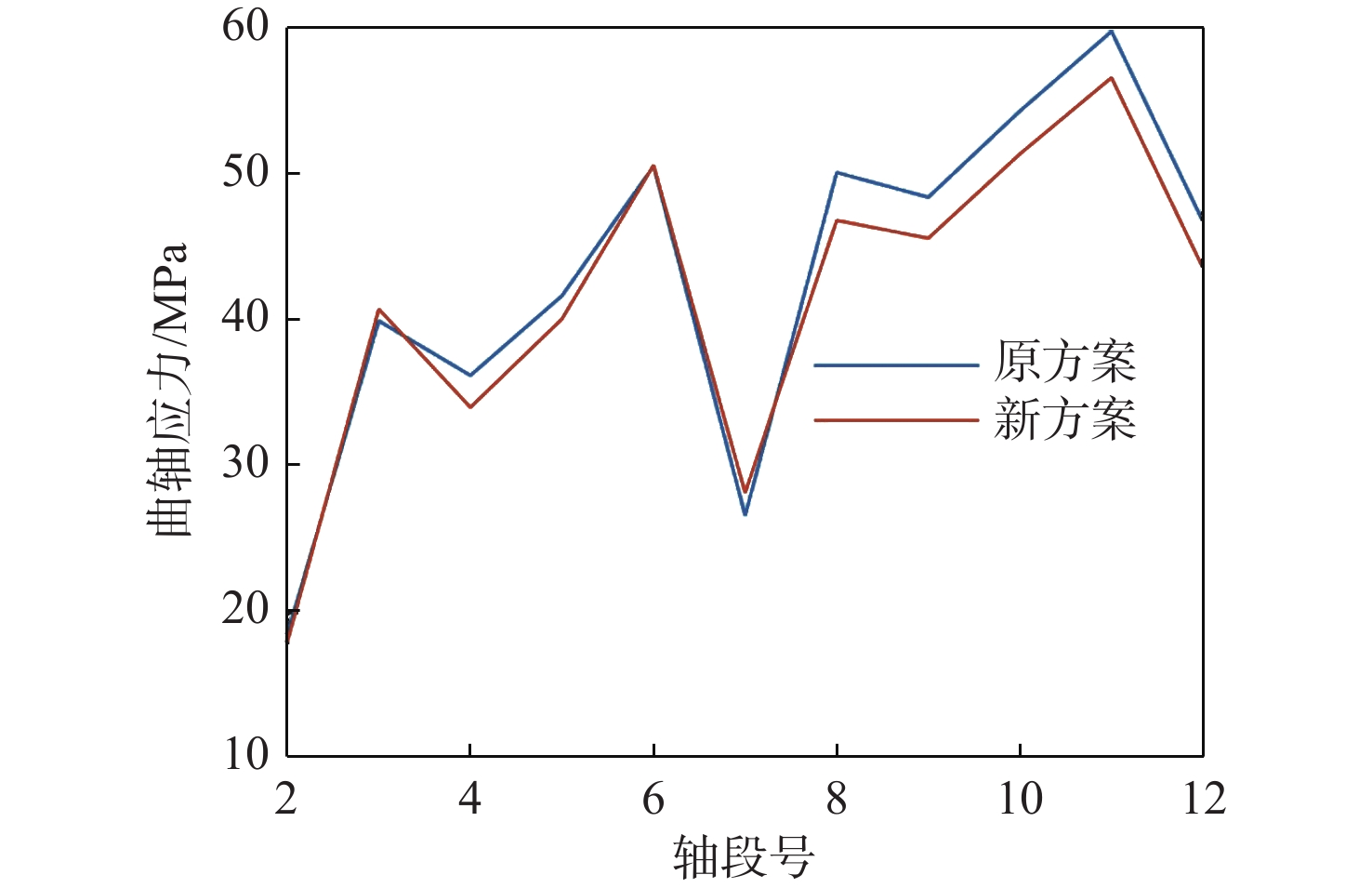
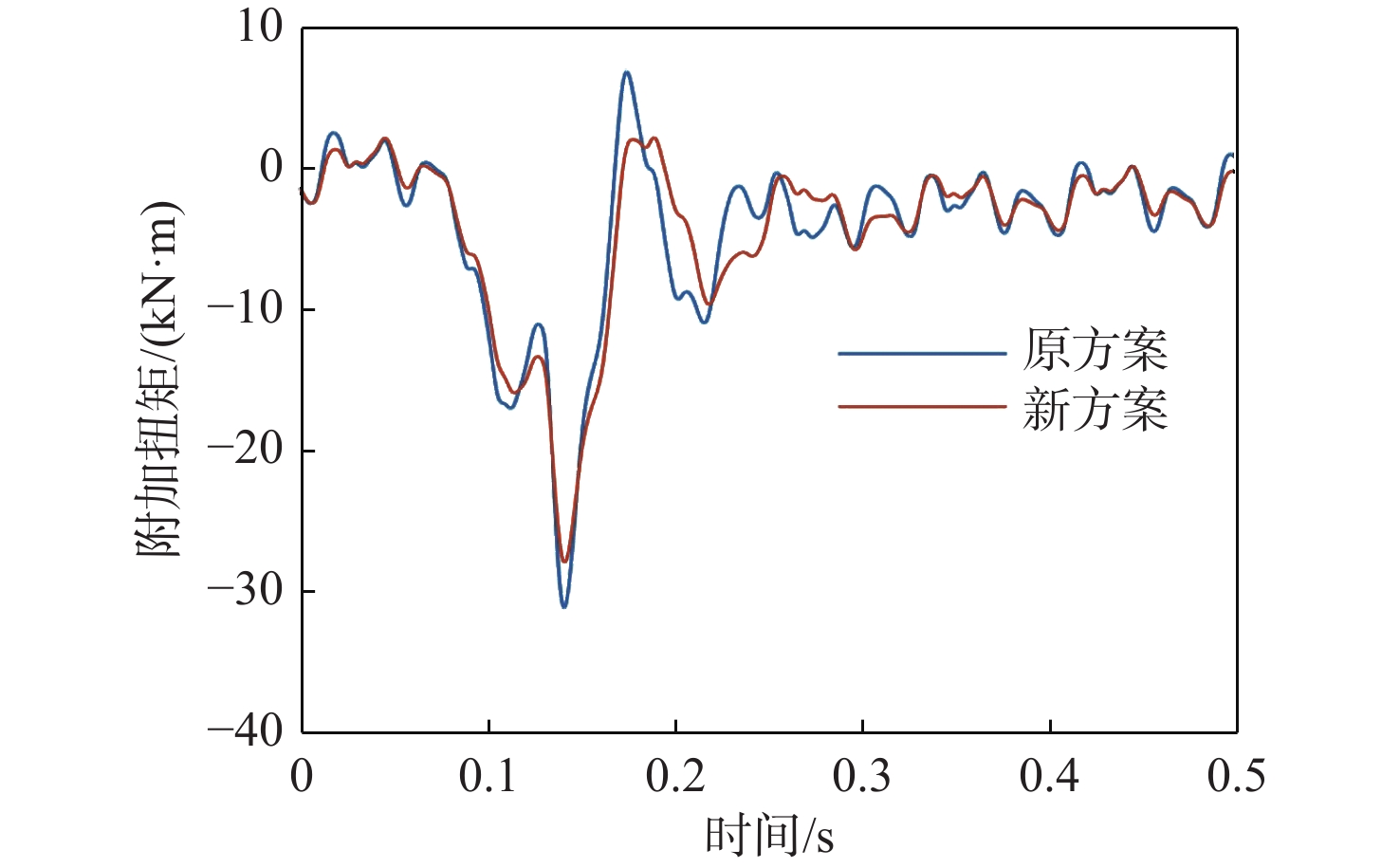
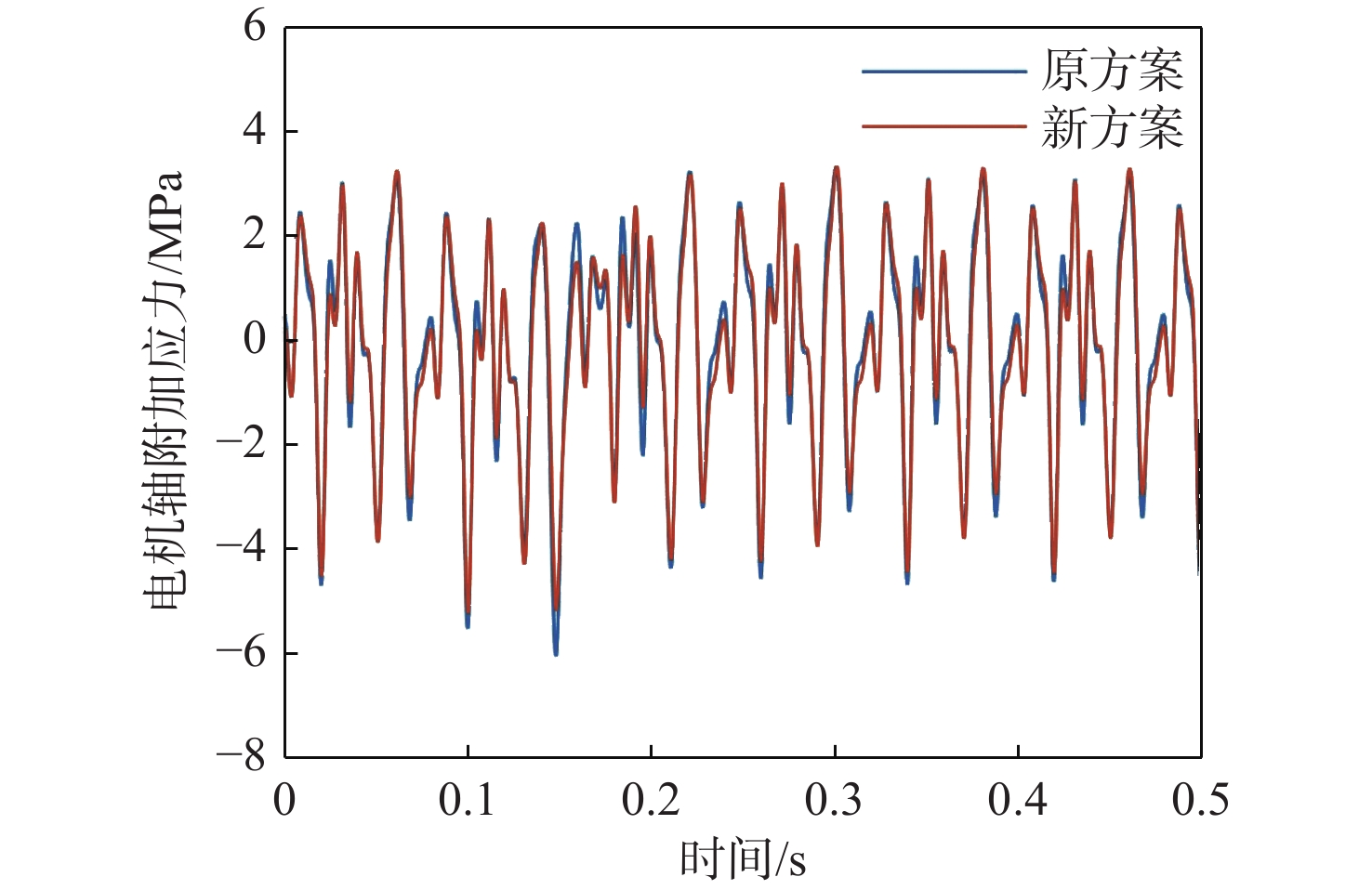
根据上文的参数影响分析结果，鉴于在完成柴油机与发电机匹配之后难以改变发电机的转动惯量，故通常采用配置弹性联轴器与减振器等措施来调整机组轴系扭振特性的工程实际情况，本文提出了新的轴系关键部件参数优化方案，即将扭振减振器刚度优选为原始值的90%（即1.233 E+06 N·m/rad），将联轴器刚度优选为原始值的70%（即0.649 E+06 N·m/rad），电机转子惯量则保持不变。基于优化后的轴系扭振参数，将计算得到的冲击扭矩施加于曲轴转角691°时的轴系扭振特性与原始参数计算结果进行对比，如图15～图17所示。

图 15 曲轴的瞬时最大应力

Figure 15. Instantaneous maximum torsional stress of crankshaft

下载: 全尺寸图片幻灯片

图 16 联轴器的瞬时最大附加扭矩

Figure 16. Instantaneous maximum additional torque of coupling

下载: 全尺寸图片幻灯片

图 17 电机轴的瞬时附加应力

Figure 17. Instantaneous torsional stress of generator rotor

下载: 全尺寸图片幻灯片

由此可见，在新的轴系参数优化方案下：短路冲击工况下的电机轴瞬时最大附加应力由6.03 MPa降至5.22 MPa，下降了13.43%；联轴器瞬时最大扭矩由31.12 kN·m降至27.85 kN·m，下降了10.51%；而曲轴各轴段的瞬时最大应力由59.72 MPa降至56.56 MPa，下降了5.29%。

4. 结　论

本文基于Newmark法，考虑发电机发生短路故障时产生的短路冲击激励对轴系瞬态扭振特性的影响，着重考虑柴油机激励和短路冲击激励相位角的影响，分析了轴系关键部件参数对短路冲击下的轴系瞬态扭振特性的影响规律，并基于此提出了新的轴系参数优化方案，得到如下结论：

1）发生短路冲击时，轴系扭振特性显著恶化，正常工况下曲轴轴段的最大应力为50.49 MPa，短路冲击作用下最大可增加至59.72 MPa。

2）柴油机激励和短路冲击激励相位角的影响不可忽略，在不同激励叠加相位下，柴油发电机组轴系曲轴轴段最大附加应力、联轴器附加扭矩、电机轴附加扭矩的最大值、最小值分别相差了9.23 MPa、5.28 kN·m和4.02 MPa。

3）基于轴系扭振参数对短路冲击下轴系瞬态扭振特性的影响规律，将扭振减振器刚度、联轴器刚度分别优选为原始值的90%和70%，短路冲击工况下的电机轴瞬时最大附加应力、联轴器瞬时最大扭矩、曲轴各轴段瞬时最大应力分别降低了13.43%，10.51%，5.29%，从而验证了新的轴系参数优化方案的有效性。

图 1 柴油机组轴系的当量模型

Figure 1. The equivalent system of diesel shafting

下载: 全尺寸图片幻灯片

图 2 柴油机动力学示意图

Figure 2. Schematic diagram of the diesel engine-kinematic

下载: 全尺寸图片幻灯片

图 3 柴油机的气缸激励合成

Figure 3. Cylinder excitation of diesel engine

下载: 全尺寸图片幻灯片

图 4 发电机的短路冲击力矩

Figure 4. Impact torque of generator under short-circuit faults

下载: 全尺寸图片幻灯片

图 5 强迫振动响应的计算流程图

Figure 5. Calculation process of forced vibration response

下载: 全尺寸图片幻灯片

图 6 曲轴各轴段的最大应力

Figure 6. Maximum torsional stress of crankshaft

下载: 全尺寸图片幻灯片

图 7 各轴段的附加扭矩

Figure 7. Additional torque of shafting

下载: 全尺寸图片幻灯片

图 8 不同冲击加入时刻下，曲轴轴段的瞬时最大应力

Figure 8. Instantaneous maximum torsional stress of crankshaft under different impact times

下载: 全尺寸图片幻灯片

图 9 不同冲击加入时刻下，联轴器的瞬时最大附加扭矩

Figure 9. Instantaneous maximum vibration torque of coupling under different impact times

下载: 全尺寸图片幻灯片

图 10 不同冲击加入时刻下，电机输入轴的瞬时附加应力

Figure 10. Instantaneous torsional stress of generator rotor under different impact times

下载: 全尺寸图片幻灯片

图 11 曲轴的瞬时最大应力

Figure 11. Instantaneous maximum stress of crankshaft

下载: 全尺寸图片幻灯片

图 12 联轴器的瞬时最大附加扭矩

Figure 12. Instantaneous maximum additional torque of coupling

下载: 全尺寸图片幻灯片

图 13 联轴器的瞬时最大相对角位移

Figure 13. Instantaneous maximum relative angular displacement of coupling

下载: 全尺寸图片幻灯片

图 14 电机轴的瞬时最大附加应力

Figure 14. Instantaneous torsional stress of generator rotor

下载: 全尺寸图片幻灯片

图 15 曲轴的瞬时最大应力

Figure 15. Instantaneous maximum torsional stress of crankshaft

下载: 全尺寸图片幻灯片

图 16 联轴器的瞬时最大附加扭矩

Figure 16. Instantaneous maximum additional torque of coupling

下载: 全尺寸图片幻灯片

图 17 电机轴的瞬时附加应力

Figure 17. Instantaneous torsional stress of generator rotor

下载: 全尺寸图片幻灯片

表 1 轴系原始参数值

Table 1 Original parameters of shafting

参数数值

联轴器刚度/(N·m·rad⁻¹) 0.927 E+06
减振器刚度/(N·m·rad⁻¹) 1.37 E+06
发电机转子惯量/(kg·m²) 200

下载: 导出CSV

参考文献(11)

[1]	马怀腾, 张权, 李东升. 某型船用大功率柴油发电机组轴系扭振分析及惯量盘设计[J]. 船舶工程, 2016, 38(Supp 2): 139-142. MA H T, ZHANG Q, LI D S. Torsional vibration analysis of a marine high power diesel generator set and design of inertia plate[J]. Ship Engineering, 2016, 38(Supp 2): 139-142 (in Chinese).
[2]	LIU Z W, WU K, DING Q, et al. Engine misfire diagnosis based on the torsional vibration of the flexible coupling in a diesel generator set: simulation and experiment[J]. Journal of Vibration Engineering & Technologies, 2020, 8(1): 163–178.
[3]	董焕彬, 王伟江, 郭耀华, 等. 联轴器特性对柴油发电机组轴系扭振性能影响研究[J]. 机械设计与制造, 2020(7): 33–38. doi: 10.3969/j.issn.1001-3997.2020.07.009 DONG H B, WANG W J, GUO Y H, et al. Study on the effect of coupling characteristics on torsional vibration performance of diesel generator shaft systems[J]. Machinery Design & Manufacture, 2020(7): 33–38 (in Chinese). doi: 10.3969/j.issn.1001-3997.2020.07.009
[4]	胡云波. 5L21/31型柴油机发电机组轴系扭振分析及齿轮异响故障诊断[D]. 哈尔滨: 哈尔滨工程大学, 2016. HU Y B. The analysis of shaft torsional vibration and gear noise fault diagnosis of 5L21/31 genset[D]. Harbin: Harbin Engineering University, 2016 (in Chinese).
[5]	KIM Y G, LEE M S, CHO K H, et al. Effects of a turbocharger cut out system on vibration characteristics of a propulsion shafting system and a large low speed marine diesel engine[J]. Journal of Mechanical Science and Technology, 2017, 31(8): 3737–3745. doi: 10.1007/s12206-017-0716-x
[6]	MIROŠEVIĆ M, MALJKOVIĆ Z, MILKOVIĆ M. The influence of impact load on torsional dynamics of generator units[C]//Proceedings of the 2011 14th European Conference on Power Electronics and Applications. Birmingham: IEEE, 2011: 1−6.
[7]	向玲, 陈秀娟, 唐贵基. 汽轮发电机组轴系扭振响应分析[J]. 动力工程学报, 2011, 31(1): 27–32. XIANG L, CHEN X J, TANG G J. Analysis on response of shaft torsional vibration in turbine-generator unit[J]. Journal of Chinese Society of Power Engineering, 2011, 31(1): 27–32 (in Chinese).
[8]	何成兵, 顾煜炯, 邢诚. 短路故障时汽轮发电机组轴系弯扭耦合振动分析[J]. 中国电机工程学报, 2010, 30(32): 84–90. HE C B, GU Y J, XING C. Coupled flexural and torsional vibrations analysis of turbine generator shaft systems caused by short circuit fault[J]. Proceedings of the CSEE, 2010, 30(32): 84–90 (in Chinese).
[9]	李晓茜, 王刚, 吕秉琳, 等. 短路工况下柴油发电机组轴系扭振计算方法及特性研究[J]. 内燃机工程, 2013, 34(2): 18–23. doi: 10.13949/j.cnki.nrjgc.2013.02.017 LI X Q, WANG G, LÜ B L, et al. Calculation method and characteristics analysis of torsional vibration of diesel generating set shaft system in short circuit condition[J]. Chinese Internal Combustion Engine Engineering, 2013, 34(2): 18–23 (in Chinese). doi: 10.13949/j.cnki.nrjgc.2013.02.017
[10]	李增光, 赵辉, 周宁. 短路冲击作用下电力推进装置扭振计算与分析[J]. 中国舰船研究, 2020, 15(6): 60–65. doi: 10.19693/j.issn.1673-3185.01902 LI Z G, ZHAO H, ZHOU N. Calculation and analysis of torsional vibration of electrical propulsion system under a short-circuit-induced impulse load[J]. Chinese Journal of Ship Research, 2020, 15(6): 60–65 (in Chinese). doi: 10.19693/j.issn.1673-3185.01902
[11]	张志华. 动力装置振动数值计算[M]. 哈尔滨: 哈尔滨工程大学出版社, 1994: 168-170. ZHANG Z H. Numerical calculation of power plant vibra-tion[M]. Harbin: Harbin Engineering University Press, 1994: 168-170 (in Chinese).

施引文献

资源附件(0)

图(17) / 表(1)

计量

文章访问数: 227
HTML全文浏览量: 32
PDF下载量: 13
被引次数: 0

0. 引　言
1. 轴系当量模型与激励分析
1.1 柴油发电机组轴系当量模型
1.2 柴油机轴系扭振激励分析
1.2.1 柴油机气缸激励形成
1.2.2 短路冲击激励
2. 轴系扭振特性分析
2.1 正常工况下轴系扭振计算
2.2 短路工况下轴系扭振计算
3. 考虑短路冲击影响的轴系参数优化
4. 结　论

0. 引　言
1. 轴系当量模型与激励分析
1.1 柴油发电机组轴系当量模型
1.2 柴油机轴系扭振激励分析
1.2.1 柴油机气缸激励形成
1.2.2 短路冲击激励
2. 轴系扭振特性分析
2.1 正常工况下轴系扭振计算
2.2 短路工况下轴系扭振计算
3. 考虑短路冲击影响的轴系参数优化
4. 结　论

参考文献(11)

施引文献

资源附件(0)

短路冲击下的船用柴油机瞬态扭振特性分析

作者简介: 徐聪聪，女，1985年生，硕士，高级工程师 梁刚，男，1977年生，博士，研究员 陶杰，男，1997年生，博士生

通讯作者: 徐聪聪

计量

出版历程

Transient torsional vibration analysis of marine diesel engine under short-circuit impact

0. 引 言

1. 轴系当量模型与激励分析

1.1 柴油发电机组轴系当量模型

1.2 柴油机轴系扭振激励分析

1.2.1 柴油机气缸激励形成

1.2.2 短路冲击激励

2. 轴系扭振特性分析

2.1 正常工况下轴系扭振计算

2.2 短路工况下轴系扭振计算

3. 考虑短路冲击影响的轴系参数优化

4. 结 论

计量

出版历程

目录

0. 引 言

1. 轴系当量模型与激励分析

1.1 柴油发电机组轴系当量模型

1.2 柴油机轴系扭振激励分析

1.2.1 柴油机气缸激励形成

1.2.2 短路冲击激励

2. 轴系扭振特性分析

2.1 正常工况下轴系扭振计算

2.2 短路工况下轴系扭振计算

3. 考虑短路冲击影响的轴系参数优化

4. 结 论

作者简介:
徐聪聪，女，1985年生，硕士，高级工程师

梁刚，男，1977年生，博士，研究员

陶杰，男，1997年生，博士生

通讯作者:
徐聪聪

0. 引　言

4. 结　论

0. 引　言

4. 结　论