0.   引　言

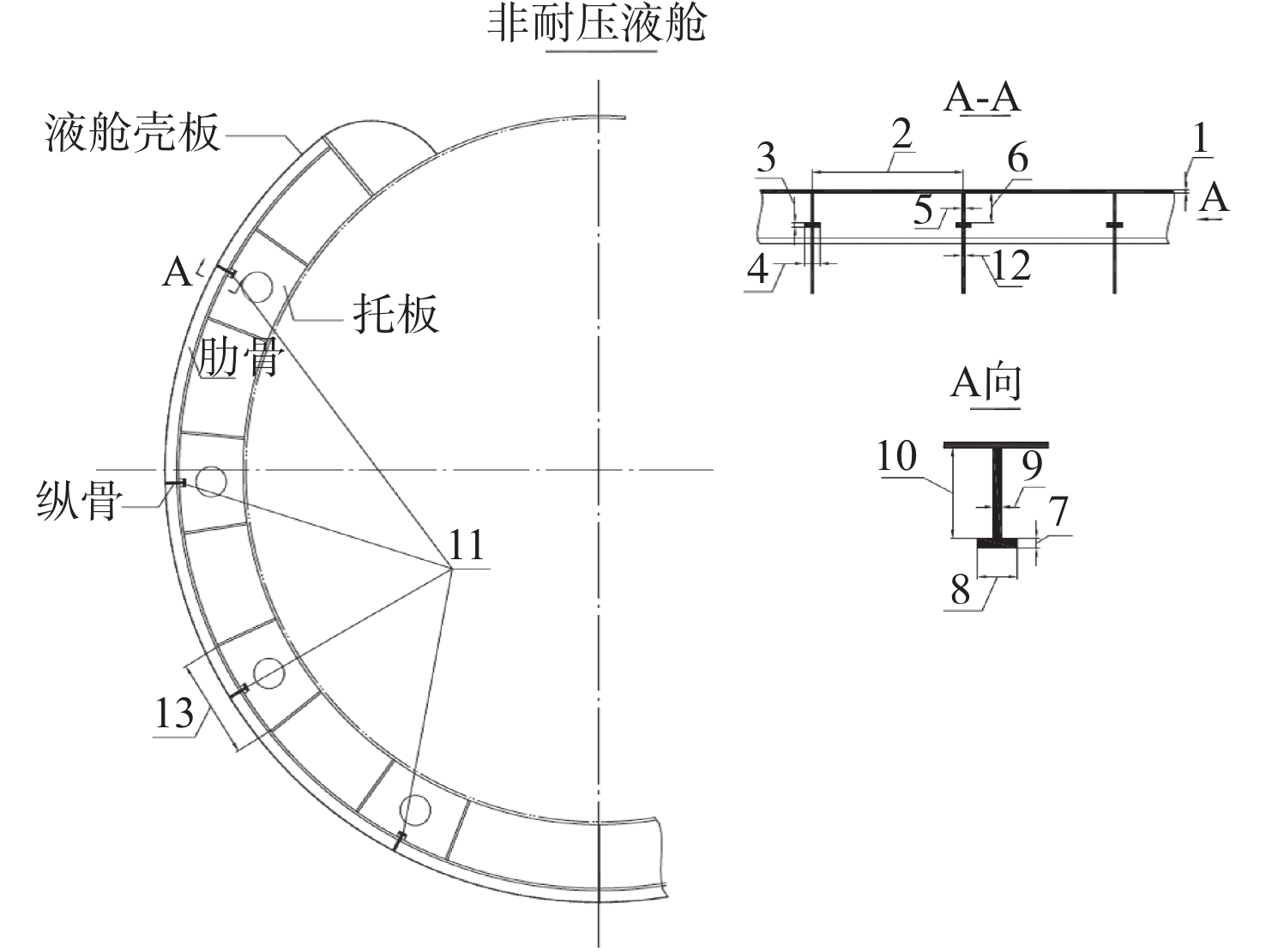
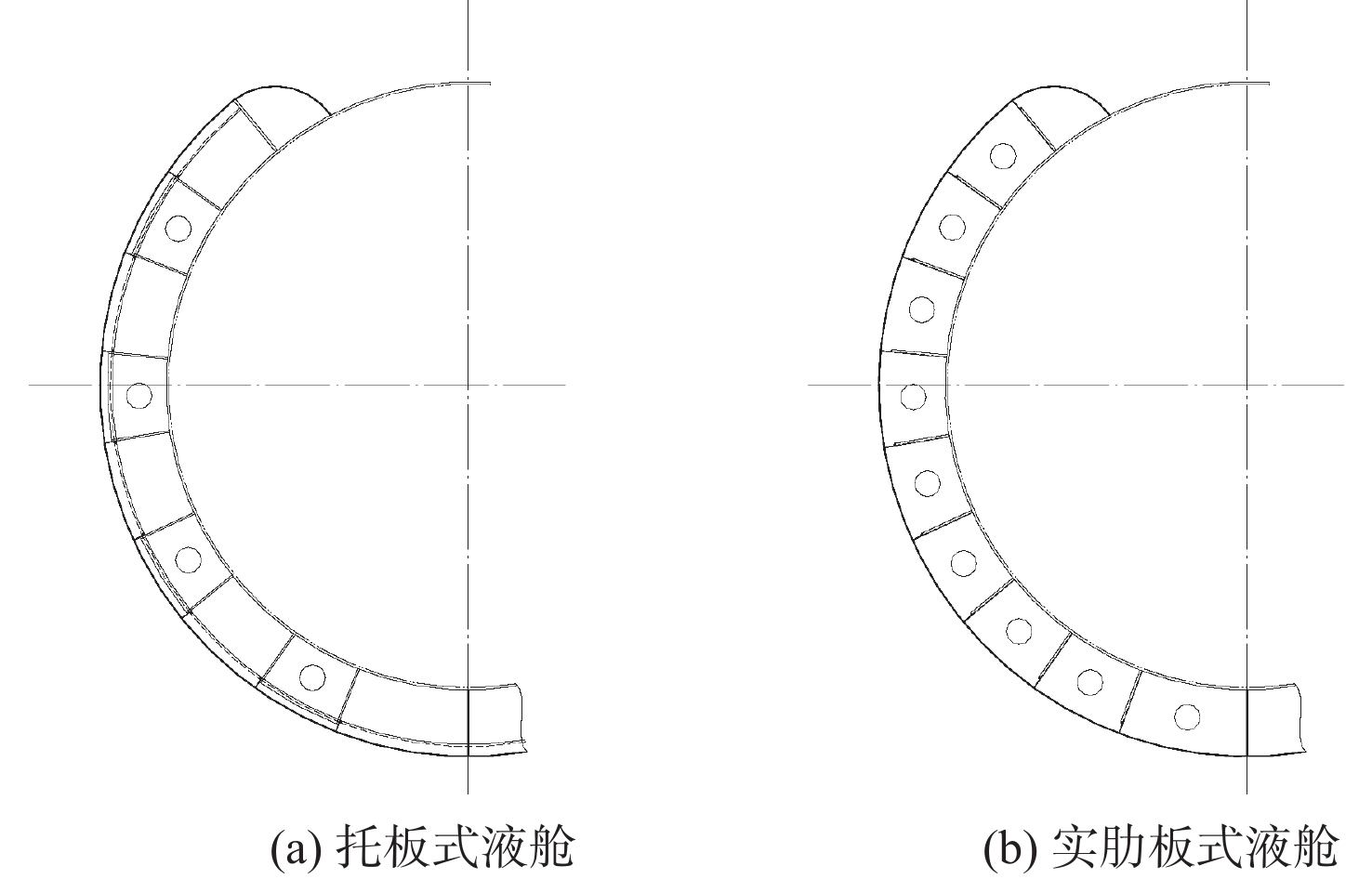
舷间液舱是双壳体潜艇重要的结构组成部分，主要包括压载水舱、燃油压载水舱、舷外燃油舱、调整水舱等。舷间液舱按照其所承受的不同工作压力分为耐压液舱和非耐压液舱两大类。耐压液舱要求能够承受与耐压船体相同的深水压力，其结构强度与耐压船体等强；而非耐压液舱不承受舷外静水压力，仅在上浮下潜时承受部分水压力，其大小由舱内外液面的高差决定，同时，在水面时，还要承受波浪冲击和其他局部载荷^[1]。耐压液舱通常采用实肋板结构，非耐压液舱通常采用托板式结构，如图1所示。

图  1  舷间液舱结构示意图

Figure  1.  Structure diagrams of tank

下载: 全尺寸图片 幻灯片

随着潜艇的下潜深度越来越大，如何在保证结构安全性和功能的前提下减轻结构重量、提高有效载荷成为了潜艇舷间液舱结构设计的一项重要课题。

耐压液舱承受着与耐压壳体相同的工作压力，一般视为耐压船体的一部分。因此，学术界对耐压液舱结构的优化研究较为深入^[2]。孙倩和谢祚水^[3]对同心圆和准同心圆式耐压液舱结构进行了优化设计；黄镇熙和王祖华^[4]利用Sysware软件对实肋板纵骨式耐压液舱进行了优化设计；戴睿婕等^[5]对外置式耐压液舱的实肋板结构进行了拓扑和尺寸优化分析；郭雨等^[6]采用自适应模拟退火算法对水面船舶方形耐压舱进行了优化设计。然而，学术界针对非耐压液舱结构优化的工作则相对较少，这主要是因为非耐压液舱的工作压力相对较低，结构重要性不及耐压液舱。但是，非耐压液舱承担着潜艇上浮和下潜的重要功能，其容积远大于耐压液舱，在整个船体结构重量中其占比也并不是可以忽略的。随着潜艇设计技术的进步，能够下潜更大深度是未来潜艇结构设计发展的重要方向，随着下潜深度的增加，对潜艇结构重量的设计要求将越来越苛刻。因此，潜艇非耐压液舱结构优化设计是十分必要的。

本文拟以某非耐压横骨架式舷间液舱结构作为算例，针对非耐压液舱壳板、肋骨、纵骨以及托板等结构尺寸的优化问题进行研究。基于模拟退火算法，利用Matlab软件编程以及其自带的Optimization Tool来实现双壳体潜艇非耐压舷间液舱的优化设计程序。在满足结构强度、稳定性及工艺性的条件下，得出最为合理的优化方案，从而达到结构减重的目的。

1.   非耐压舷间液舱结构模拟退火优化设计方法

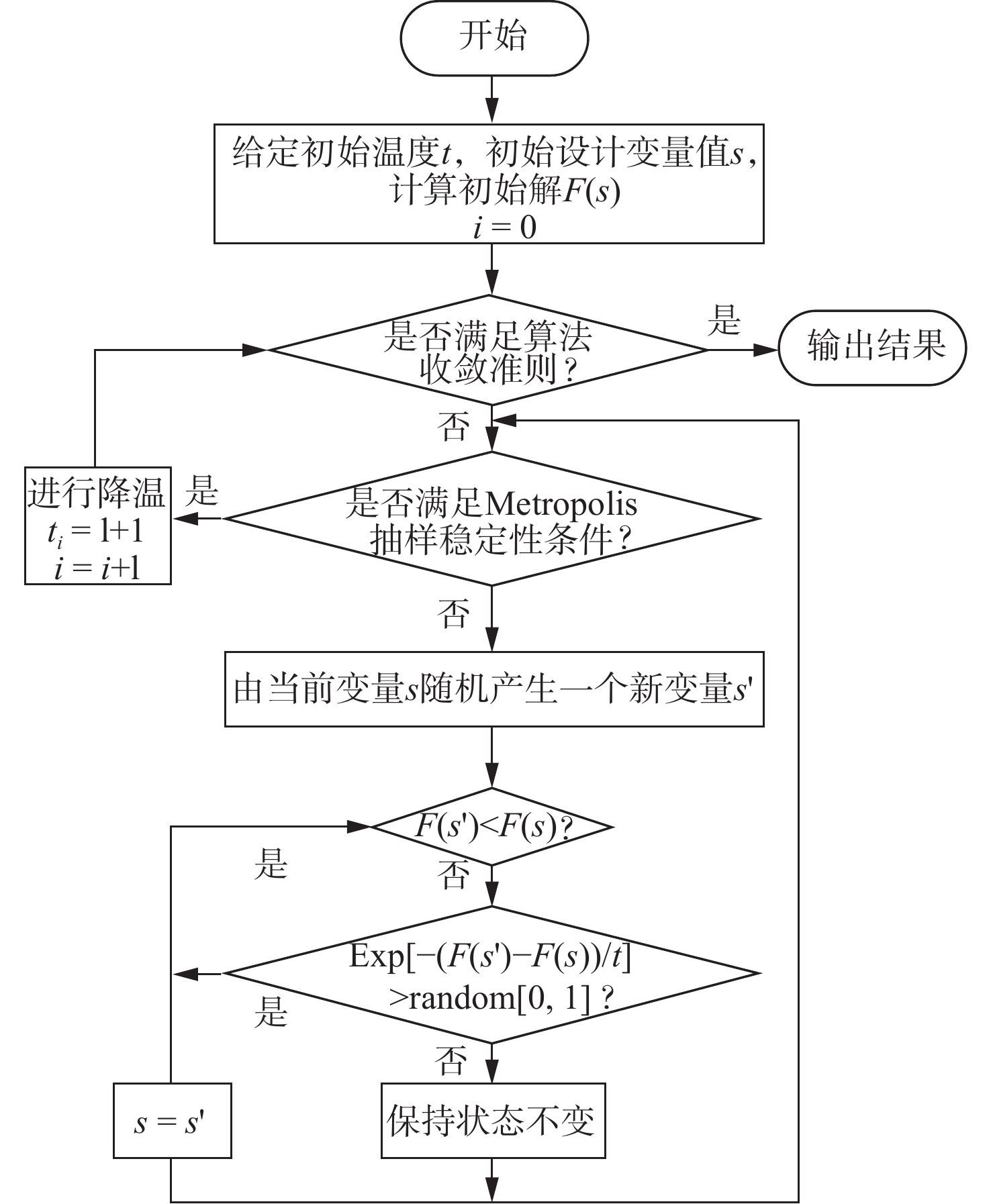
本文采用模拟退火算法对非耐压舷间液舱结构进行优化设计。模拟退火算法是以固体退火过程的物理现象和统计物理学原理为背景，基于蒙特卡罗迭代求解策略的一种随机优化算法。该算法的特点是，在一个初始温度下，随着温度的不断下降，结合概率突跳特性，求解目标函数的全局最优解。固体退火包括加温、等温和冷却3个过程，其中等温过程是为了使物理系统在每个温度下都能够达到平衡态，随着物理系统的缓慢冷却，系统能量的降低趋于最小值。表1列出了物理退火过程与优化问题的相似性，图2所示为模拟退火算法的流程。

表  1  物理退火与优化问题的相似性

Table  1.  Similarity of annealing and optimization

物理退火	优化问题
粒子状态	解
能量最低状态	最优解
熔解过程	设定初始温度
等温过程	Metropolis抽样
冷却过程	控制参数下降
能量	目标函数

下载: 导出CSV 

| 显示表格

图  2  模拟退火算法流程图

Figure  2.  Flow chart for simulated annealing algorithm

下载: 全尺寸图片 幻灯片

模拟退火算法主要利用的几个参量体现在图2中的第2个处理框中。其中，t表示的参量为温度，实际是模拟退火算法的一个控制参数；s表示的参量为设计变量，是一个复杂的包含13个变量的集合，并将在1.1.1节中详述；F(s)表示的参量为目标函数，并将在1.1.2节中阐述。

由图2可见，模拟退火算法由内循环和外循环构成，内循环称之为Metropolis算法，外循环为降温过程。模拟退火算法的内循环参数设计主要包括状态产生函数和状态接受函数，状态产生函数主要用于随机产生设计变量s，而状态接受函数的要点在于如何以一定的概率接受劣化解，从而使整个算法趋向全局最优，其具体实现方式将在1.2节中详述。而外循环设计主要包括温度更新函数和外循环终止准则等，其具体实现方法将在1.3节中详述。

本文将结合非耐压液舱的特点，建立结构优化数学模型，进行目标函数和约束条件的处理，并分别对模拟退火算法的内外循环进行设计。为了寻找全局最优解，模拟退火算法通常需要较高的初始温度、较慢的降温速率和较低的终止温度以及各温度下足够多的抽样次数^[7]，而这导致了算法的优化时间过长。因此，需要大量的试验来确定较优的算法参数。

本文采用Matlab编程以及其自带的Optimization Tool相结合的方法对非耐压舷间液舱进行优化设计。Matlab编程主要解决设计变量、目标函数以及约束条件的处理，利用Optimization Tool内置的模拟退火算法进行计算。

1.1   非耐压舷间液舱优化数学模型

1.1.1   设计变量

非耐压舷间液舱存在横骨架和纵骨架2种结构形式。本文主要讨论横骨架托板式舷间液舱，如图3所示。本文舷间液舱肋骨和纵骨均采用T型肋骨结构，设计变量共有13个，包括：1−非耐压舷间液舱壳板厚度t_s，2−液舱肋骨间距l，3−肋骨面板厚度t_f，4−肋骨面板宽度b_f，5−肋骨腹板厚度d_f，6−肋骨腹板高度h_f，7−纵骨面板厚度t_z，8−纵骨面板宽度b_z，9−纵骨腹板厚度d_z，10−纵骨腹板高度h_z，11−纵骨个数n，12−托板厚度t_t，13−托板长度b_t。由于结构材料的板厚是根据钢材订购厂家的尺寸规格确定的，且型材结构尺寸应满足相应的工艺性要求，因此所有设计变量均为离散设计变量。

图  3  非耐压液舱优化设计变量示意图

Figure  3.  Schematic of design variables for non-pressure tank

下载: 全尺寸图片 幻灯片

1.1.2   目标函数

本文优化方案的设计目标是在满足结构强度和几何尺寸约束的前提下，使非耐压舷间液舱结构重量最小。由于非耐压舷间液舱结构的壳板和型材选用的钢材密度是一致的，因此目标函数可以由结构的总体积代替，即

式中：Int[ ]表示取整函数; R为非耐压舷间液舱壳板半径；L为液舱总长度；α为液舱壳板所在范围的弧度；d_y为液舱高度。

1.1.3   约束条件

1） 结构强度约束。

非耐压舷间液舱主要按照GJB/Z 226—2006《潜艇非耐压船体结构设计计算方法》^[8]进行设计。需要校核的应力包括：液舱壳板跨中中面周向应力$\sigma _2^0$和外压下的失稳临界压力P_E、肋骨弯曲应力$\sigma _{\rm{B}}^{\rm{f}}$和剪应力$\tau _{\rm{f}}^{}$、纵骨弯曲应力$\sigma _{\rm{B}}^{{\mathrm{{z}}}}$和剪应力$\tau _{{\mathrm{{z}}}}^{}$以及托板正应力$\sigma _{\rm{te}}^{}$以及失稳临界应力$\sigma _{\rm{cr}}^{}$。以下所述为这些力需满足的结构强度约束条件。

（1） 非耐压舷间液舱壳板跨中中面周向应力$\sigma _2^0$为

式中：$K_2^0$是计算参数，可依据文献[8]中相关规定取值；P_ci为非耐压舷间舷间液舱的计算内压力，σ_s为非耐压舷间液舱结构材料的屈服强度。

（2） 非耐压舷间液舱壳板外压下的失稳临界压力P_E为

式中：K是计算参数，可依据文献[8]中相关规定取值；E为非耐压舷间液舱结构材料的弹性模量；μ为泊松比；c为纵骨之间的壳板拱高；b为纵骨之间壳板的投影长度；P_co为非耐压舷间舷间液舱的计算外压力。

（3） 肋骨弯曲应力$\sigma _{\rm{B}}^{\rm{f}}$和剪应力$\tau _{\rm{f}}^{}$分别为：

式中：a为肋骨最大长度；$W_{\rm{ep}}^{\rm{f}}$为肋骨的弹塑性剖面模数；$A_{\rm{f}}^{}$为肋骨截面面积。

（4） 纵骨弯曲应力$\sigma _{\rm{B}}^{{\mathrm{{z}}}}$和剪应力$\tau _{{\mathrm{{z}}}}^{}$为

式中：b为纵骨间距；$W_{\rm{ep}}^{{\mathrm{{z}}}}$为纵骨的弹塑性剖面模数；$A_{{\mathrm{{z}}}}^{}$为纵骨截面面积。

（5） 托板正应力$\sigma _{\rm{te}}^{}$：

式中：S为托板周向间距；$A_{\rm{t}}^{}$为托板最小处截面面积。

（6） 托板失稳临界应力$\sigma _{\rm{cr}}^{}$：

式中：η为计算参数，可依据文献[8]中相关规定取值；σ为外压下托板正应力；I为托板最小处惯性矩。

2） 结构型材几何约束。

根据GJB 4000—2000《舰船通用规范总册——船体结构》^[9]中的相关规定以及设计实践经验，非耐压舷间液舱肋骨和纵骨还需满足以下几何约束

式中：$A_{\rm{mb}}^{}$为型材（包括肋骨和纵骨）的面板剖面积；$A_{\rm{fb}}^{}$为型材的腹板剖面积。

综上可知，本文非耐压舷间液舱结构优化模型中有结构强度约束8个，几何尺寸约束10个，一共18个约束条件，如表2所示。

表  2  非耐压舷间液舱优化约束条件

Table  2.  Constraint conditions for non-pressure tank optimization

约束类型	约束条件		约束类型	约束条件
几何约束	${{{b_{\rm{f}}}} / {{t_{\rm{f}}}}} - 10 \leqslant 0$		几何约束	$0.3{{ - {A_{\rm{zmb}}}} / {{A_{\rm{zfb}}}}} \leqslant 0$
几何约束	${{{h_{\rm{f}}}} /{{d_{\rm{f}}}}} - 40 \leqslant 0$		强度约束	$\sigma _{\text{2}}^{\text{0}} - 0.85{\sigma _{\rm{s}}} \leqslant 0$
几何约束	${{{b_{\mathrm{z}}}}/ {{t_{{\mathrm{{z}}}}}}} - 10 \leqslant 0$		强度约束	${P_{\rm{co}}} - {P_{\rm{E}}} \leqslant 0$
几何约束	${{{h_{{\mathrm{{z}}}}}} / {{d_{{\mathrm{{z}}}}}}} - 40 \leqslant 0$		强度约束	$\sigma _{\rm{B}}^{\rm{f}} - {\sigma _{\rm{s}}} \leqslant 0$
几何约束	${{{d_{\rm{f}}}}/ {{t_{\rm{f}}}}} - 1 \leqslant 0$		强度约束	${\tau _{\rm{f}}} - 0.57{\sigma _{\rm{s}}} \leqslant 0$
几何约束	${{{d_{{\mathrm{{z}}}}}} / {{t_{{\mathrm{{z}}}}}}} - 1 \leqslant 0$		强度约束	$\sigma _{\rm{B}}^{\textit{z}} - {\sigma _{\rm{s}}} \leqslant 0$
几何约束	${{{A_{\rm{fmb}}}} / {{A_{\rm{ffb}}}}} - 0.7 \leqslant 0$		强度约束	${\tau _{\mathrm{z}}} - 0.57{\sigma _{\rm{s}}} \leqslant 0$
几何约束	$0.3{{ - {A_{\rm{fmb}}}} / {{A_{\rm{ffb}}}}} \leqslant 0$		强度约束	$\sigma _{\rm{te}}^{} - {\sigma _{\rm{s}}} \leqslant 0$
几何约束	${{{A_{\rm{zmb}}}} / {{A_{\rm{zfb}}}}} - 0.7 \leqslant 0$		强度约束	$\sigma - {\sigma _{\rm{cr}}} \leqslant 0$
注：${A_{\rm{fmb}}}$和${A_{\rm{ffb}}}$表示肋骨面板和腹板的面积，${A_{\rm{zmb}}}$和${A_{\rm{zfb}}}$表示纵骨面板和腹板的面积

下载: 导出CSV 

| 显示表格

1.1.4   约束条件的处理

约束条件有2种处理方法^[10]：一种是检验法，即对所有约束逐个检验，只有全部满足要求的解才会进行目标值的比较；二是罚函数法，即采用该函数将约束函数转移到增广目标函数上，使有约束的问题转化为无约束的问题。因罚函数的设置非常依赖于经验，故本文采用了检验法对约束予以处理。

1.2   内循环设计

1.2.1   离散变量的状态产生函数

利用随机数设置状态函数时，将针对每个设计变量产生一个随机数。对于离散变量，需要随机数与其之间建立完全映射，但离散变量之间基本没有规律可循，建立映射并不容易。鉴于Matlab中变量的矩阵化，矩阵中各元素的下标与随机数建立映射则相对容易。因此，本文采用文献[11]中提出的方法建立离散变量的状态产生函数。例如，由2～10 mm不等的壳板厚度t_s构成液舱壳板厚度数组（t_s={t_s1,t_s2,...,t_sm}），共有m个变量。随机变量与壳板厚度之间组成的映射使用Matlab伪代码可表示为

式中：rand( )为随机数生成函数，随机生成[0，1]之间的随机数。

1.2.2   状态接受函数

状态接受函数又被称为Metropolis准则，其主要特点是参考了固体物理中的退火过程，以概率性的方法接受新状态，避免了优化函数限于局部最优解。

对于优化问题，其中的设计变量s以及对应的目标函数F(s)可以类比为固体的一个微观状态i和对应的能量E_i，当固体发生微小变化时，到达另一个状态j，其对应的能量为E_j。当E_j<E_i时，新状态可直接取代前一状态；当E_i<E_j时，新状态是否取代前一状态要考虑热运动的影响，即依据概率方法进行判别。其表达式为

式中：P_T为状态接受概率；T为当前温度。

1.3   外循环设计

1.3.1   温度更新函数

由于基于物理准平衡态理论分析的温度更新函数计算繁琐且不成熟。在Matlab的Optimization Tool组件中，提供了3种温度更新函数：指数衰减、对数衰减和线性衰减。

指数衰减函数的表达式如下：

式中，α取值范围为0 < α < 1；k表示循环次数。

对数衰减函数的表达式如下：

线性衰减函数的表达式如下：

式中：K_n为算法温度下降的总次数；t₀为初始温度。

经过计算，发现对数衰减函数的计算效率较低，指数衰减函数与线性衰减函数计算效率相当。因此，本文采用指数衰减函数进行计算。

另外，在外循环中还需确定初始温度。Optimization Tool组件中默认的初始温度是100 ℃，经实际计算发现，将初始温度提升至更高时（500 ℃，1000 ℃，5000 ℃，10000 ℃），优化的效率和精度并没有得到显著的提升，因此本文采用默认的初始温度进行计算。

1.3.2   外循环终止准则

外循环终止准则用于决定算法何时结束。一般包括如下几种方法：

1） 设置终止温度。给定一个很小的正数ε，当温度小于ε时，输出最优解。

2） 设置迭代次数。设置一个较大的数K_n，当温度迭代次数超过K_n时，算法终止，输出最优解。

3） 目标函数容差。在某一个温度下，给定的迭代次数内没有改进当前最优解或者最优解的值在某个很小的容差范围内，算法终止，输出最优解。

根据实际计算，发现终止温度值很难达到。一般是到达最大迭代次数或者达到目标函数容差时计算终止，Optimization Tool组件中默认的最大迭代次数为3000乘以变量个数，对于本文即为39000次，目标函数容差默认值为1×10⁻⁶。

2.   液舱结构优化实际算例

2.1   非耐压液舱初始结构

选取横骨架托板式非耐压液舱作为研究对象，采用相关规范^[8-9]进行初步结构设计。非耐压舷间液舱的初始结构参数如下：

1） 液舱壳板初始板厚为8 mm，液舱初始肋骨间距为500 mm。

2） 肋骨及纵骨均采用T型材设计。肋骨参数为：腹板10 mm×100 mm，面板15 mm×54 mm；纵骨参数为：腹板11 mm×100 mm，面板14 mm×52 mm。

3） 沿非耐压壳板圆周方向每20°设置1个托板，托板厚度为6 mm。

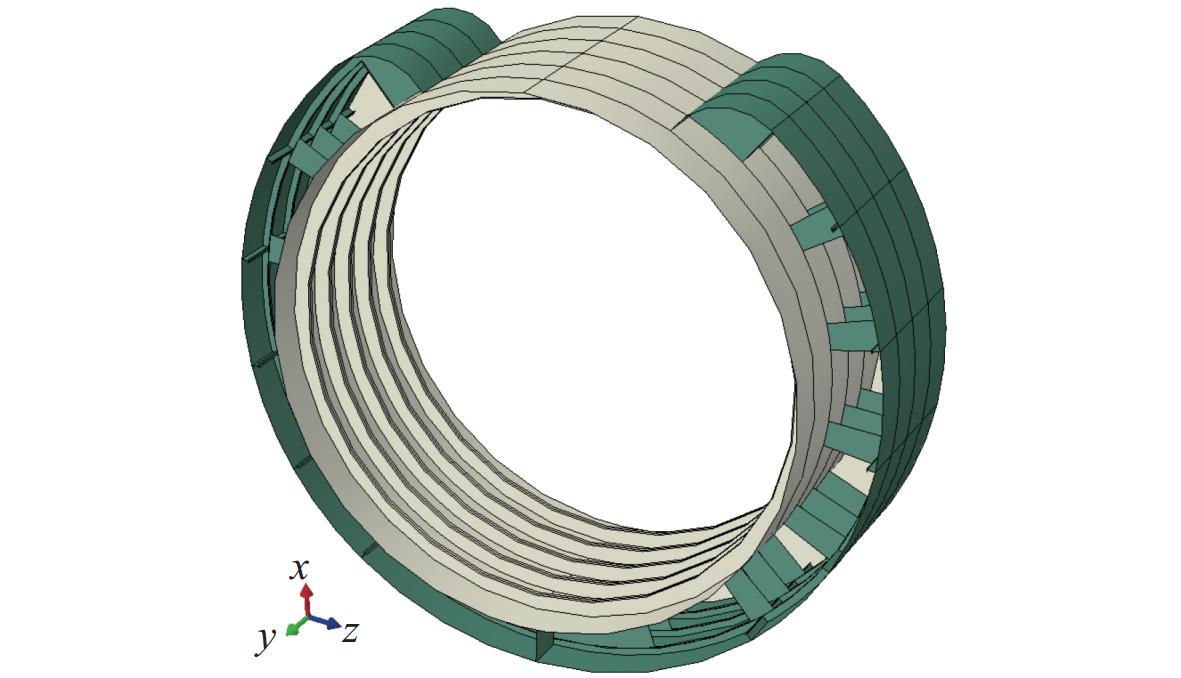
非耐压液舱几何模型如图4所示。图中，绿色部分为非耐压液舱，是本文主要研究的结构；浅黄色部分为耐压结构，主要起到支撑非耐压液舱的作用，不参与优化设计。

图  4  非耐压液舱几何模型

Figure  4.  Geometrical model of non-pressure tank

下载: 全尺寸图片 幻灯片

2.2   非耐压液舱结构优化设计

设计变量的取值范围如表3所示，优化计算结果如表4所示（两表中，除纵骨个数外，其他变量单位均为mm）。优化后的主要参数如下：

表  3  设计变量取值范围

Table  3.  Data range of design variables

设计变量	取值范围
液舱壳板厚度ts	6～10
肋骨间距l	450～500
肋骨面板厚度${t_{\rm{f}}}$	3～32
肋骨面板宽度${b_{\rm{f}}}$	30～120
肋骨腹板厚度${d_{\rm{f}}}$	3～32
肋骨腹板高度${h_{\rm{f}}}$	40～300
纵骨面板厚度${t_{\mathrm{z}}}$	3～32
纵骨面板宽度${b_{\mathrm{z}}}$	30～120
纵骨腹板厚度${d_{\mathrm{z}}}$	3～32
纵骨腹板高度${h_{\mathrm{z}}}$	40～300
纵骨个数n	3～11
托板厚度${t_{\rm{t}}}$	3～6
托板长度${b_{\rm{t}}}$	50～600

下载: 导出CSV 

| 显示表格

表  4  非耐压舷间液舱优化结果对比

Table  4.  Comparison of optimized and initial values for non-pressure tank

设计变量	初始值	优化值	相对变化量
液舱壳板厚度ts	8	6	−25%
肋骨间距l	500	480	−4%
肋骨面板厚度${t_{\rm{f}}}$	15	12	−20%
肋骨面板宽度${b_{\rm{f}}}$	54	46	−14%
肋骨腹板厚度${d_{\rm{f}}}$	10	8	−20%
肋骨腹板高度${h_{\rm{f}}}$	100	100	0
纵骨面板厚度${t_{\mathrm{z}}}$	14	11	−21%
纵骨面板宽度${b_{\mathrm{z}}}$	52	48	−8%
纵骨腹板厚度${d_{\mathrm{z}}}$	11	9	−18%
纵骨腹板高度${h_{{\mathrm{{z}}}}}$	100	103	+3%
纵骨个数n	5	5	0
托板厚度${t_{\rm{t}}}$	6	3	−50%
托板长度${b_{\rm{t}}}$	400	400	0

下载: 导出CSV 

| 显示表格

1） 液舱壳板初始板厚为6 mm，液舱初始肋骨间距为480 mm。

2） 肋骨及纵骨均采用T型材设计。肋骨参数为：腹板8 mm×100 mm，面板12 mm×46 mm；纵骨参数为：腹板9 mm×103 mm，面板11 mm×48 mm。

3） 沿非耐压壳板圆周方向每20°设置1个托板，托板厚度为1.2 mm。

根据GJB 8741—2015《舰艇用10CrNiCu钢板规范》^[12]，板材的最小厚度值为3 mm，因此对托板优化结果进行了工艺性改进优化。由表可见，除纵骨腹板高度相比初始值略有增加外，其他参数相比初始值有所减小或者保持不变。优化结果体积由表5可见，相比于初始方案，在满足所有约束条件的前提下，优化后的结构体积降低了约27.2%。

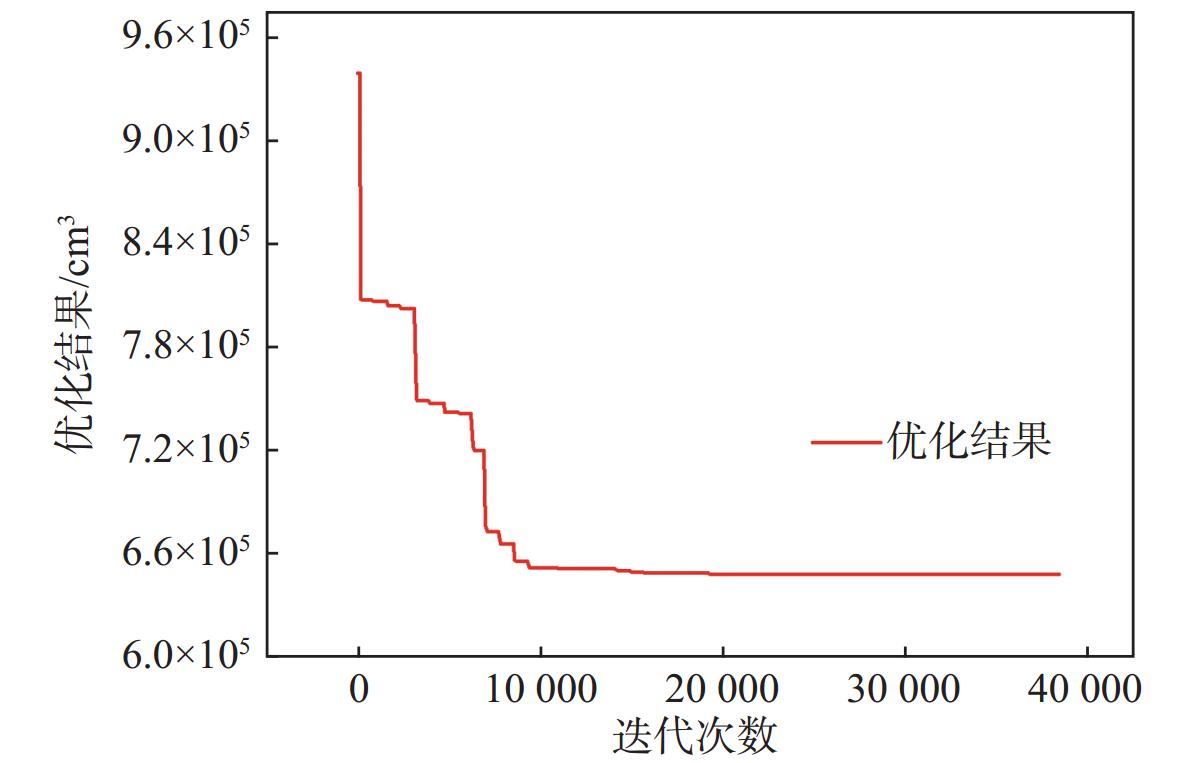
表  5  非耐压舷间液舱优化结果体积对比

Table  5.  Comparison of optimal volumes for non-pressure tank

结构位置	结构体积变化率
壳板	−15.98%
肋骨	−7.04%
纵骨	−1.59%
托板	−2.59%

下载: 导出CSV 

| 显示表格

由图5所示的目标函数优化过程收敛曲线可见，优化结果在初始迭代区域就迅速收敛，说明本文所用算法具有良好的优化效率。

图  5  非耐压舷间液舱优化收敛曲线

Figure  5.  Convergence curve of non-pressure tank optimization

下载: 全尺寸图片 幻灯片

2.3   结构方案对比

通过模拟退火算法得到了优化后的结构参数，将其与初始设计结果进行对比，如表6所示。

表  6  非耐压舷间液舱结构强度计算结果

Table  6.  Result of strength calculation for non-pressure tank

计算部位的应力	规范计算值/MPa		许用值/MPa
	优化前	优化后
板格跨中中面应力	127.4	173.8	≤331.5
肋骨弯曲应力	284.1	385.7	≤390
肋骨剪应力	112.2	194.9	≤222.3
纵骨弯曲应力	94.3	103.9	≤390
纵骨剪应力	104.8	120.6	≤222.3
托板正应力	61.2	239.3	≤390
板格稳定性	5.77	3.06	≥0.196
托板稳定性	15.4 ≤ 180.4	60.3 ≤ 287.3	−

下载: 导出CSV 

| 显示表格

由表6所示结构优化前后的规范计算值可见，结构优化后，各应力分量相比初始方案均有不同程度的增加，但均小于许用应力，其中肋骨弯曲应力已经接近许用值。

3.   结　语

本文提出了一种基于模拟退火算法的非耐压舷间液舱结构的优化计算方法，较好地解决了双壳体潜艇非耐压舷间液舱离散变量的复杂优化问题，并提升了计算效率。优化算例显示，优化的方案相比初始方案的结构体积减小了27.2%，各项指标均在约束范围内，优化效果良好。由表5中优化前后结果的对比可以看出，壳板体积优化占整个结构优化体积的比例最大，其次是肋骨和托板，最后是纵骨。由表4中的各优化参数值和表6中的规范计算值可知，肋骨已经接近许用应力，此时再减小板厚，肋骨将具有超过许用应力的风险，说明优化已经接近最优。在满足规范应力约束、几何约束和施工工艺要求的前提下，本文所提方案中的壳板和托板初始设计较为保守。因此，出于减轻结构重量的考虑，非耐压舷间液舱的壳板和托板的厚度可适当减薄。

本文优化算法具有一定的普适性，可为其他船体结构优化问题提供借鉴和参考。