0.   引　言

传统的混合动力船舶一般是指电动机和柴油发动机相结合的动力系统，随着新能源技术的迅猛发展，光伏、液化天然气（liquefied natural gas，LNG）、燃料电池等新能源技术也开始应用于混合动力船舶，而超级电容–电池复合储能^[1]、燃料电池^[2]以及直流电网^[3]等新兴技术也逐渐进入了大众视野。对于多类能源耦合的船舶，如何在不同工况下进行功率合理分配是影响船舶动力系统性能的重要因素，所以有必要开展混合能源船舶能量管理方面的研究。

混合动力船舶的能量管理是一个多目标优化的问题，涵盖了机械能、化学能及电能等能量的转换与控制技术，同时需考虑船舶的安全稳定运行要求，并可在此基础上进一步优化船舶运行的经济性和环保性。基于单一的管理目标而言，现有的能量管理策略主要分为：以考虑电能质量为主、以考虑故障恢复为主、以考虑能耗排放为主、以考虑系统经济性为主的能量管理目标。

兰熙等^[4]借助构建电池荷电状态的补偿函数来研究电池的荷电状态，通过将补偿函数列为优化目标，并引入评价函数的权重系数中，从而使电池的电荷状态保持在设定值附近，以提升电池健康状态。Srivastava等^[5]选用基于决策支持系统的自动重构方法研究了船舶供配电系统故障后的恢复问题，并参照供配电系统的动态数据和网络拓扑结构对故障后的供配电系统进行了恰当的能量管理和规划，从而确保了重要系统的正常运行。Stone等^[6]针对以电池–超级电容作为复合储能系统的燃料电池船舶开展了能量管理研究，保证了船舶供配电系统在复杂工况和功率需求波动剧烈工况下的正常运行，提高了混合动力船舶电网的电能质量。

混合动力船舶的能量管理主要分为2类：基于实际工程的规则型和基于不同优化目标的优化型，规则型即根据人为经验和试验来制定混合动力系统的运行模式，该策略已广泛应用于工程实践中，但其缺点是无法在复杂工况下保持最优的控制策略；优化型即通过分析对象的特征来确定优化目标和约束条件，并在此基础上构建整体优化模型，进而采用优化算法对目标函数进行求解。

目前，已有大量学者针对混合动力船舶的能量管理开展了相关研究工作：Bassam等^[7]提出了基于经典比例积分控制器的能量管理策略，从而改进了燃料电池的工作效率；Yuan等^[8]针对柴电混合动力船舶提出了一种基于DP-MPC的能量管理策略，但其并未考虑设备的使用寿命影响；Kalikatzarakis等^[9]将等效消耗最小化策略（ECMS）应用于混合动力船舶，从而实现了不同设备之间的实时功率分配。

然而，上述研究的优化对象均仅为能量管理策略，并没有同时对动力系统的设备参数选取进行匹配优化，故本文拟以Alsterwasser号燃料电池船作为研究对象，采用灰狼算法对动力系统的设备参数与能量管理策略进行匹配优化，并通过搭建船舶动力系统的Matlab/Simulink仿真模型，以验证该能量管理算法的有效性。

1.   研究对象

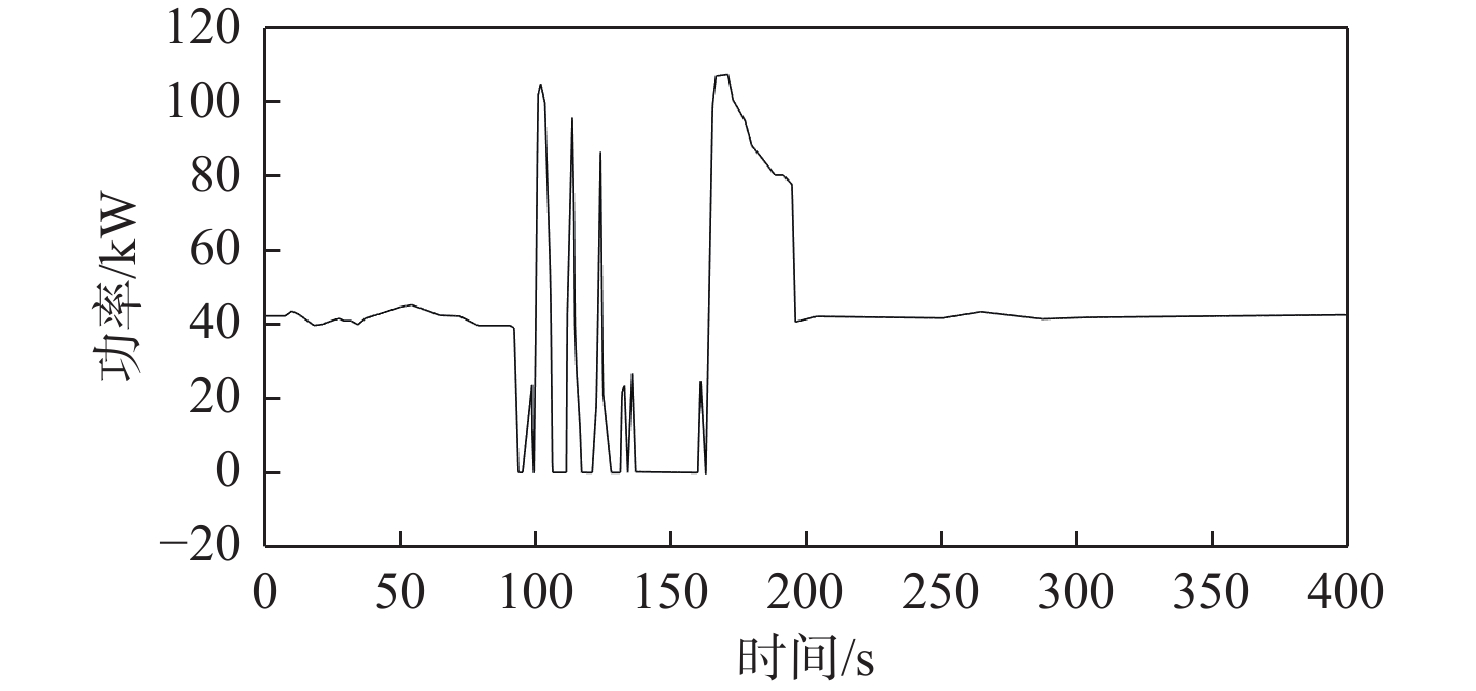
Alsterwasser号燃料电池船由欧盟零排放船舶（zero emission ship）项目资助开发^[10]，该项目始于2006年底，结束于2010年4月，旨在提供适用于水面舰艇的技术解决方案，该船的相关参数如表1所示。图1为该燃料电池船的典型功率负载。船舶包含两种不同运行状态，其中，在90～200 s船舶处于机动航行状态，负载波动剧烈，船舶功率需求在0～115 kw剧烈波动。而在其余时刻，船舶处于定速航行状态，负载功率平稳在42 kw左右；该负载工况曲线包含复杂工况，在小型船舶研究中有着重要影响。本文采用该典型工况进行设计仿真分析。

表  1  Alsterwasser号燃料电池船的参数

Table  1.  Parameters of Alsterwasser fuel cell ship

参数	数值
电池（铅凝胶）电压/ V	560
电池（铅凝胶）容量/ （A·h）	360
排水量/t	72
船长/m	25.56
船宽/m	5.20
载客量/人	100
最大速度/（km·h−1）	15

下载: 导出CSV 

| 显示表格

图  1  Alsterwasser号燃料电池船的功率负载

Figure  1.  Power load of the Alsterwasser fuel cell ship

下载: 全尺寸图片 幻灯片

2.   混合动力系统结构

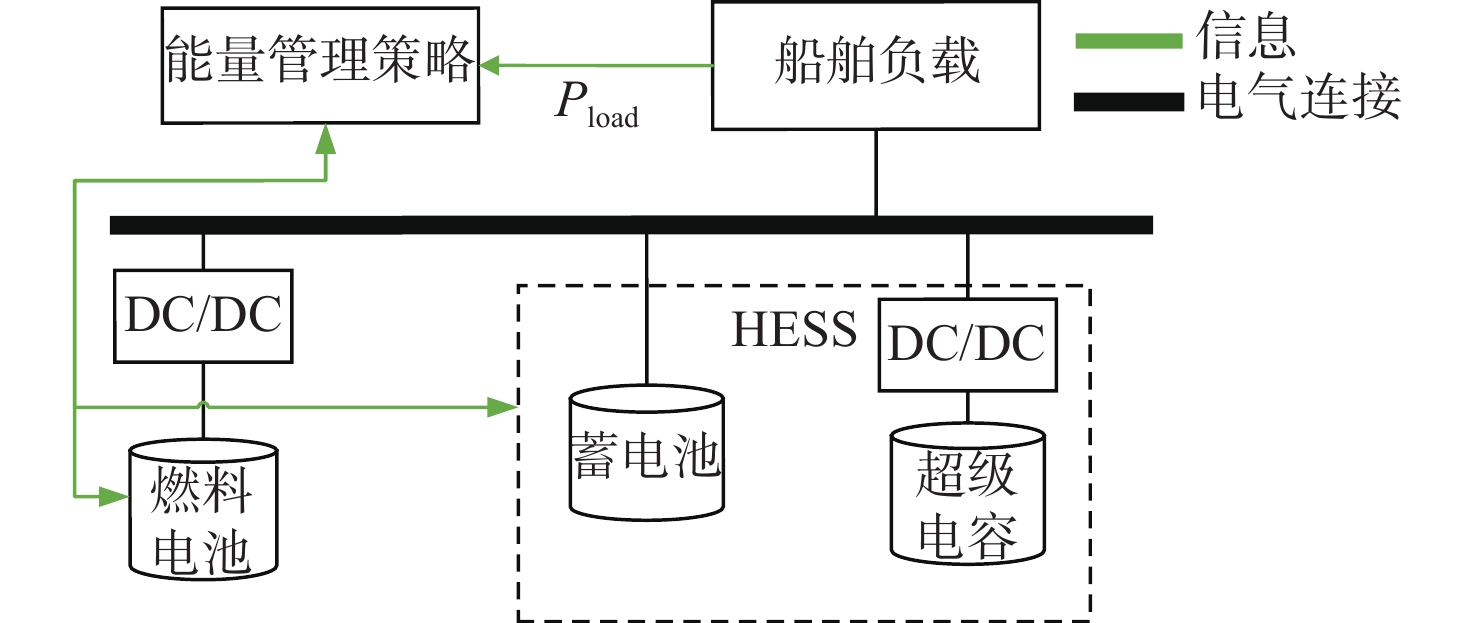
锂电池的能量密度高，但响应速度慢；而超级电容器具有响应速度快、循环寿命长等优点，本文将采用由超级电容和锂电池组成的复合储能系统（hybrid energy storage system，HESS）来替代原船动力系统的电池，其拓扑结构如图2所示，其中P_load为船舶负载功率。

图  2  燃料电池混合动力系统的拓扑结构

Figure  2.  Topological structure of fuel cell hybrid power system

下载: 全尺寸图片 幻灯片

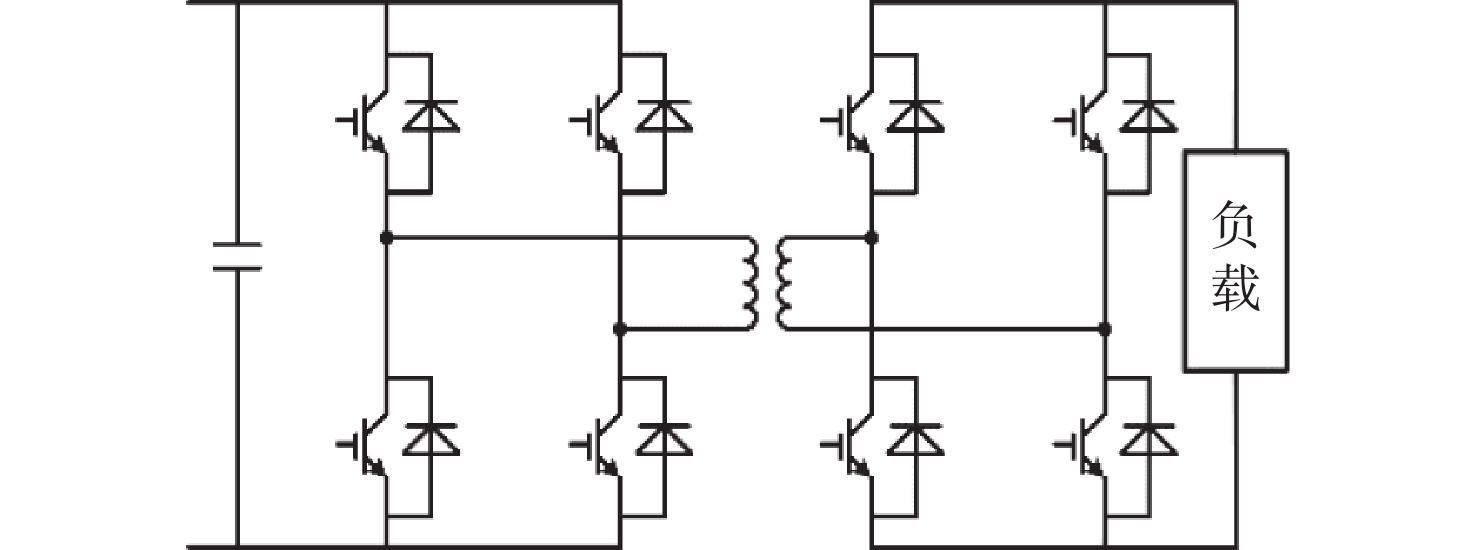
图2中，原船动力系统的燃料电池通过单向DC/DC变换器连接至直流母线，而本文的复合电源则采用了半主动式拓扑结构，超级电容通过双向DC/DC变换器与锂电池并联，其中燃料电池为主电源，复合电源为辅助电源。由文献^[10]可知，燃料电池模块一般采用Boost型单向DC/DC变换器，而超级电容模块一般采用双向全桥DC/DC变换器（图3），并采用移相控制策略对超级电容的输出功率进行调节^[11]。

图  3  双向全桥DC/DC拓扑示意图

Figure  3.  Schematic diagram of bidirectional full bridge DC/DC topology

下载: 全尺寸图片 幻灯片

3.   能量管理策略

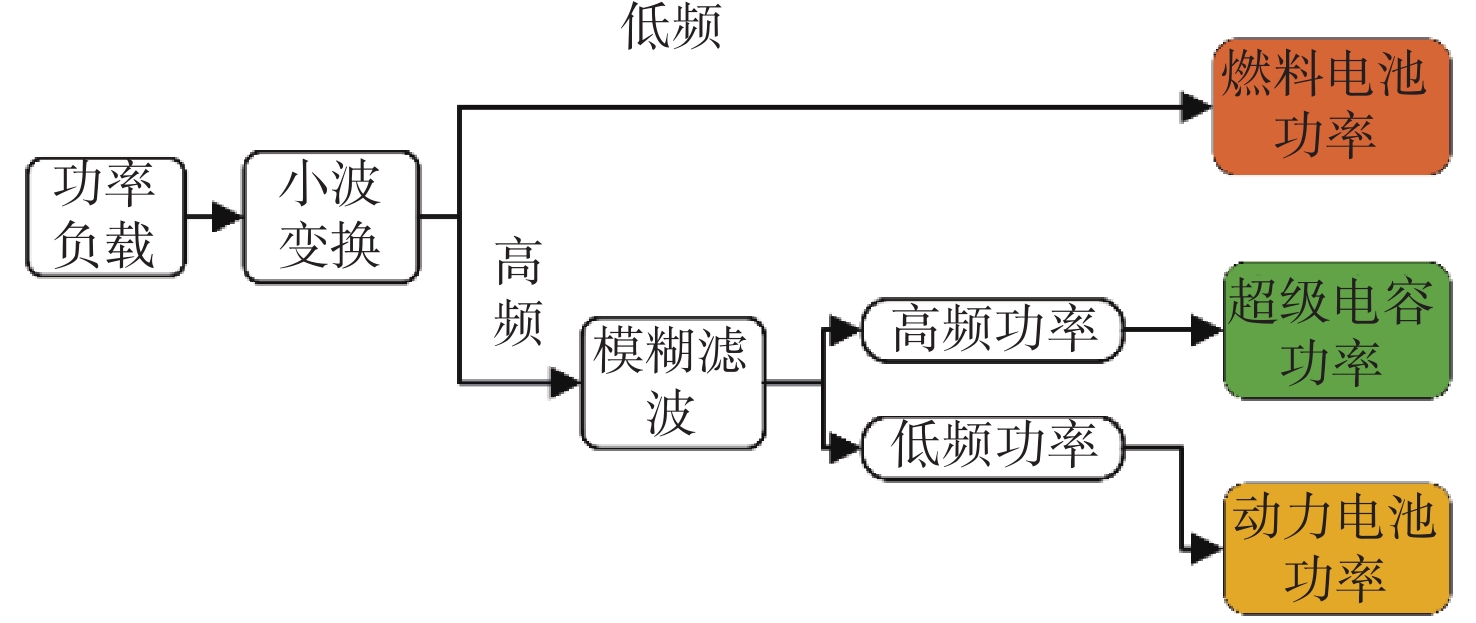
本文的能量管理策略（图4）以考虑电能质量为主，由小波变换算法和复合储能系统控制两部分组成。首先，对船舶功率需求数据进行采集；然后，采用小波变换对功率需求进行处理，其中功率需求的低频部分由燃料电池模块承担，而剩余的功率需求部分则由复合储能系统模块承担。

图  4  能量管理策略

Figure  4.  Energy management strategy

下载: 全尺寸图片 幻灯片

本文的复合储能系统将采用模糊逻辑控制策略，提供综合考虑锂电池荷电状态（state of charge，SOC），超级电容SOC和复合储能系统功率需求，对复合储能系统所承担的功率进行分解处理，其中低频部分由锂电池模块承担，而剩余部分则通过控制DC/DC变换器由超级电容模块承担。

3.1   小波变换

小波变换是一种信号的时频分析方法，与傅立叶变换相比，其可提供一个随频率变化的“时频”窗口，从而实现对信号的局部分析，故在能量管理领域的应用较为广泛。船舶的功率需求是实时信号，可以利用离散小波变换将船舶的功率需求分解为高频信号和低频信号，然后将低频信号依次通过高通滤波器和低通滤波器进行分解^[12]。

连续小波变换的表达式$W(\lambda ,\mu )$为

式中：$\lambda$为尺度因子；$x(t)$为功率信号；$\psi$为母波函数；t为时间；$\mu$为平移因子。

令$\lambda = {2^j}$，$\mu ={2}^{j}·k$，其中$j,k \in {\bf{Z}}$，Z为整数集，将式（1）的连续小波变换$W(\lambda ,\mu )$转为离散小波变换$W(j,k)$，即

逆变公式为

由于Haar小波具有最优的时域分辨率，并且Haar小波的公式与其逆变换公式相同，所以在实际控制系统中更容易实现，其表达式${\psi _{\text{H}}}(t)$如下：

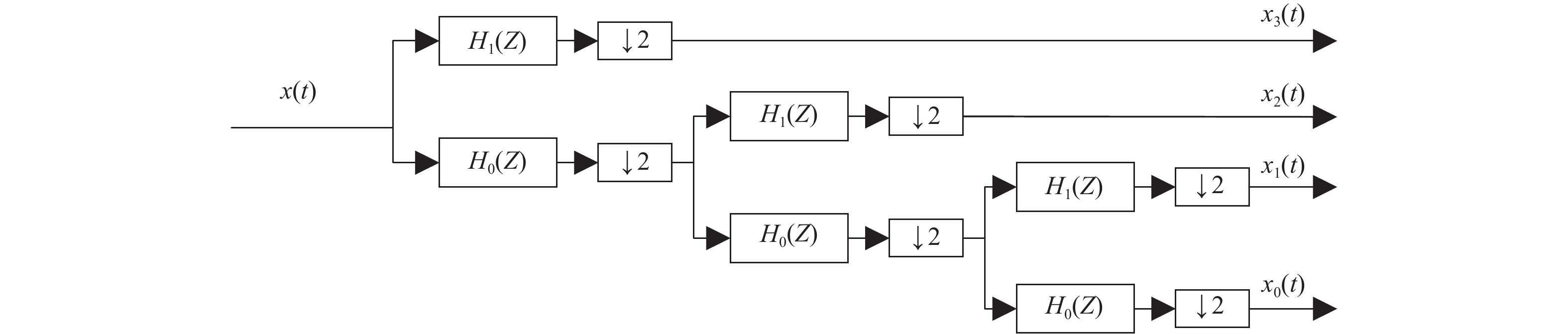
小波分解的具体过程如图5所示：首先，基于高通滤波器${H_1}(Z)$和低通滤波器${H_0}(Z)$进行Haar小波变换，使原始的功率信号$x(t)$经滤波后分解为高频信号${x}_{1}(t)，{x}_{2}(t)，{x}_{3}(t)$和低频信号${x_0}(t)$；然后，通过重构高通、低通滤波器，得到重构信号。

图  5  小波分解过程

Figure  5.  Wavelet decomposition process

下载: 全尺寸图片 幻灯片

随着小波分解层数的增加，分配给复合电源的功率也越多。复合电源作为辅助电源，其主要功能是削峰补谷，而燃料电池才是主要电源，故小波分解的层数不宜过高。本文拟采用3阶Haar小波变换，根据混合动力系统的特点，将功率需求的低频信号${x_0}(t)$分配给燃料电池承担，而高频信号${x_1}(t),{x_2}(t),{x_3}(t)$则由复合储能系统承担。

3.2   复合储能系统能量管理

模糊逻辑控制（fuzzy logic control，FLC）作为一种有效的控制方法，因其固有的鲁棒性和对非线性问题的处理能力等优点而得以广泛应用。对于复杂多变的船舶工况而言，采用模糊控制进行实时功率分配的效果非常好^[13]。

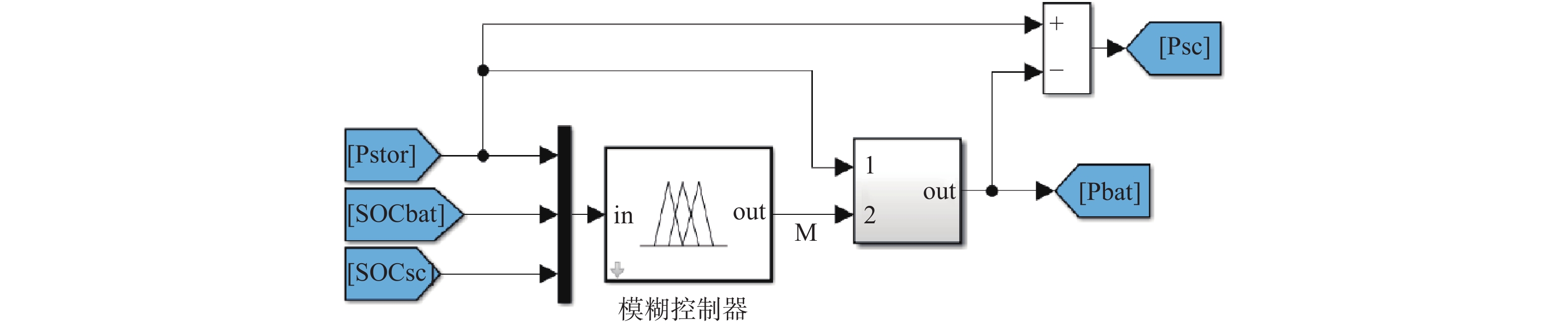
由上文可知，复合储能系统主要承担负载功率需求的高频部分。针对复合储能模块，本文设计了基于模糊控制器的复合储能系统能量管理策略，如图6所示，该策略通过对复合储能系统所承担的功率需求进行分配，从而协调各设备的能量。

图  6  复合储能系统的能量管理仿真图

Figure  6.  Energy management simulation diagram of composite energy storage system

下载: 全尺寸图片 幻灯片

基于图6的模糊控制器，根据锂电池SOC，超级电容SOC和复合储能系统功率，即可确定功率分配模块输入——功率分配系数M，以调节锂电池所需承担的功率，而复合储能系统功率的剩余部分则由超级电容承担。

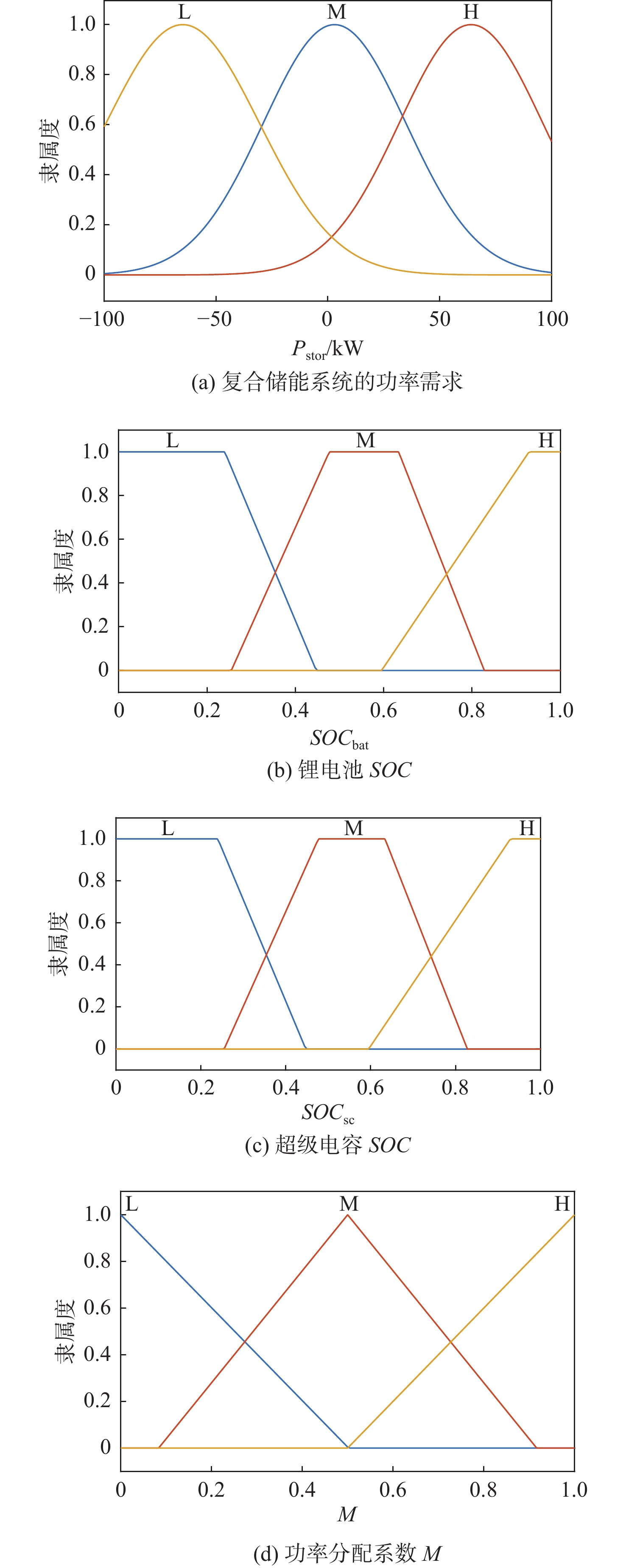
模糊控制器的隶属度函数如图7所示，相应的模糊规则如表2所示，其中：$S O{C_{{\text{bat}}}}$，$S O{C_{{\text{sc}}}}$分别为锂电池、超级电容的荷电状态值；${P_{{\text{stor}}}}$为复合电源的功率需求； L，M，H分别表示低、中、高3种状态。当复合电源的功率需求较高时，模糊控制将令超级电容器承担更多的功率需求；反之，则令锂电池承担更多的功率需求。同时，当电池或超级电容的电量过低时，将优先考虑使其承担功率信号的负功率部分；而当其电量过高时，则将优先考虑使其承担功率信号的正功率部分。

图  7  输入/输出的隶属度函数

Figure  7.  Input/output membership function

下载: 全尺寸图片 幻灯片

表  2  模糊规则

Table  2.  Fuzzy rule

超级电容SOC	锂电池SOC	功率分配系数M
		${P_{{\text{stor}}}}$=L	${P_{{\text{stor}}}}$=M	${P_{{\text{stor}}}}$=H
$S O{C_{{\text{sc}}}}$=L	$S O{C_{{\text{bat}}}}$=L	L	H	L
	$S O{C_{{\text{bat}}}}$=M	L	H	M
	$S O{C_{{\text{bat}}}}$=H	L	H	M
$S O{C_{{\text{sc}}}}$=M	$S O{C_{{\text{bat}}}}$=L	M	H	L
	$S O{C_{{\text{bat}}}}$=M	L	H	L
	$S O{C_{{\text{bat}}}}$=H	L	H	L
$S O{C_{{\text{sc}}}}$=H	$S O{C_{{\text{bat}}}}$=L	M	H	L
	$S O{C_{{\text{bat}}}}$=M	M	H	L
	$S O{C_{{\text{bat}}}}$=H	L	H	L

下载: 导出CSV 

| 显示表格

在图6的功率分配模块中，本文采用了典型一阶低通滤波器$L(s)$作为控制策略中的滤波设备，其表达式如下：

式中：s为拉普拉斯变换中的复变量；T为滤波器的时间常数，时间常数越大，则通过滤波器的高频功率部分越小，锂电池承担的功率需求也越平稳。

如果复合电源在低电量工况下继续放电，将会严重损害其使用寿命；反之，如果在高电量时继续充电，则可能导致电源损坏甚至自燃。一般来说，安全工作区间的SOC=[0.2，0.8]，因此，当复合电源SOC超过安全区限值时，应采用充放电保护措施。

当复合电源SOC处于正常充/放电区时，即可按照上述表2功率分配结果（表2）进行充放电；当复合电源处于过放区时，则不允许放电，仅能充电；当复合电源处于过充区时，则不允许充电，仅能放电。

3.3   约束条件

为保护燃料电池和复合储能系统的正常运行，在满足功率负载需求的同时，还需建立相应的系统约束^[14]：

式中：${P_{{\text{bat}}}}$，${P_{{\text{fc}}}}$，${P_{{\text{sc}}}}$分别为锂电池、燃料电池、超级电容的输出功率；${P_{\text{N}}}$为典型工况的功率需求；${V_{{\text{sc}}}}$为超级电容电压，其工作电压不能低于0.5倍的最大电压${V_{\max }}$；${I_{{\text{fc}}}}$，${I_{{\text{sc}}}}$，${I_{bat}}$分别为燃料电池、超级电容和锂电池的输出电流，均不能超过其相应的最大输出电流（${I_{{\text{fc,max}}}}$，${I_{{\text{sc,max}}}}$，${I_{{\text{bat,max}}}}$）。

4.   参数优化

灰狼算法具有结构简单、控制参数少、易于实现等优点，故被广泛应用于参数最优选择和模式识别分类等问题。本节将采用灰狼算法与燃料电池混合动力系统仿真相结合的优化方法，以混合动力系统能量损失、直流母线电压为指标建立评价船舶动力系统的目标函数，并将根据系统约束来确定复合储能系统相关参数的取值范围，进而采用灰狼算法对目标函数进行优化计算，最终得到复合储能系统相关设备参数的配置方案。

4.1   优化目标

为评价复合储能系统参数设计和动力系统设计的优劣，在考虑设备成本的基础上，本文将从直流母线电压和动力系统能量损失这2个方面进行评价。

1）直流母线电压波动的评价公式${C_1}$为

式中：i=1，2，…，N，表示采样时刻，其中N 为总的采样数量；${V_{{\text{dcbus}}}}(i)$，${V_{{\text{dcbus}}}}(i - 1)$分别为i时刻和i-1时刻的直流母线电压，单位为V。

2）系统能量损失的评价公式${C_2}$为

式中：${R_{{\text{sc}}}}$，${R_{{\text{bat}}}}$分别为超级电容、锂电池的内阻，单位为Ω；$I_{{\text{sc}}}^{}(i)$，$I_{{\text{bat}}}^{}(i)$分别为第i时刻超级电容、锂电池的电流，单位为A；${\mu _{{\text{dc}}}}$为DC/DC变换器的效率，取值0.8；${P_{{\text{dc}}}}(i)$为第i时刻DC/DC变换器的功率，单位为kW。

3）系统设备成本J为

式中：${C_{{\text{bat}}}}$为锂电池总成本；${N_{{\text{ref}}}}$为超级电容的数量；${M_{{\text{sc}}}}$为超级电容的单价。

本文以燃料电池混合动力船舶作为研究对象，故其优化目标更注重于船舶电网质量的改善^[15]。从能量管理的目标而言，即更注重提高系统能量的利用率，因此，本文将引入权重系数来设定优化目标函数：

式中：C为系统目标函数值，其值越小，则表示系统参数越接近算法的寻优目标；$\alpha$，$\beta$分别为母线电压波动、系统能量损失的权重系数，由于本文的研究对象为小型燃料电池船，故选择将母线电压作为评价函数的主要目标，最终的权重系数取值为：$\alpha$=0.65，$\beta$=0.35。

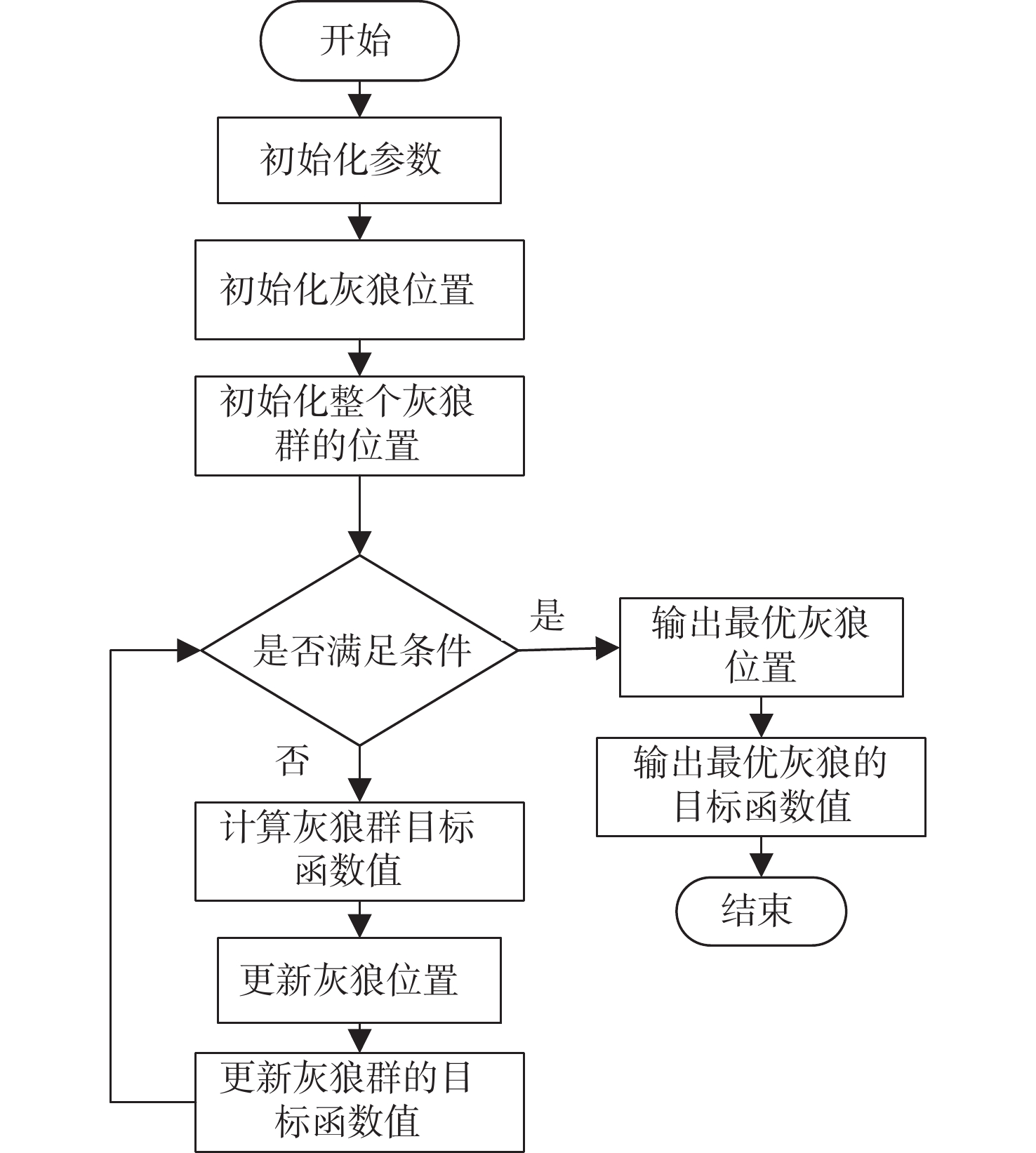
4.2   灰狼算法计算

对于上文建立的目标函数，本节将采用灰狼算法进行优化计算（图8），以得到超级电容的电压配置方案及滤波器的时间常数值。根据目标船型的电力系统参数，采用了40${\text{A}} \cdot {\text{h}}$容量的锂电池，电压设定为570 V；采用了额定电压48 V超级电容，根据文献[16]可知，根据约束条件，串联超级电容组的电压参考范围为${V_{{\text{sc}}}}$=288～576 V；一阶低通滤波器的时间常数设定为T=10～20 s。

图  8  灰狼优化算法流程

Figure  8.  Grey wolf optimization algorithm flow

下载: 全尺寸图片 幻灯片

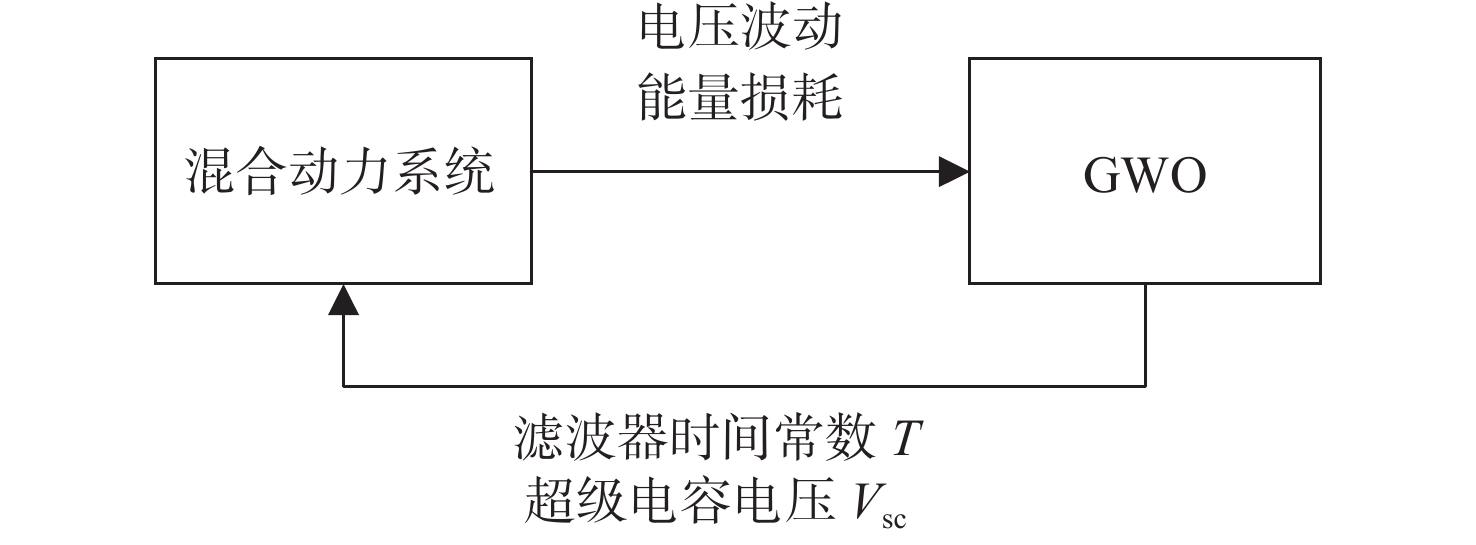
基于灰狼优化算法，本节将在Matlab/Simulink环境下对混合动力系统进行建模仿真（图9），进而优化复合储能系统中的滤波器时间常数和超级电容电压的设定参数。首先，在灰狼（GWO）算法中设定超级电容电压、滤波器时间常数的优化范围，其中${V_{{\text{sc}}}}$=288～576 V，T=10～20 s，将这2个优化变量代入动力系统仿真模型中进行仿真；然后，对模型仿真所得的电压波动、能量损失进行评估，并利用评价函数来判定优化结果的优劣。在灰狼算法优化过程中，所设定得最大迭代次数为100次，种群数量为50，相应得参数优化结果如表3所示，因此，最终选择超级电容电压为384 V。

图  9  系统优化流程图

Figure  9.  System optimization flow chart

下载: 全尺寸图片 幻灯片

表  3  参数优化结果

Table  3.  Parameter optimization result

优化参数	优化结果
超级电容电压${V_{{\text{sc}}}}$/V	392.42
滤波器时间常数T/s	14.32

下载: 导出CSV 

| 显示表格

5.   仿真分析

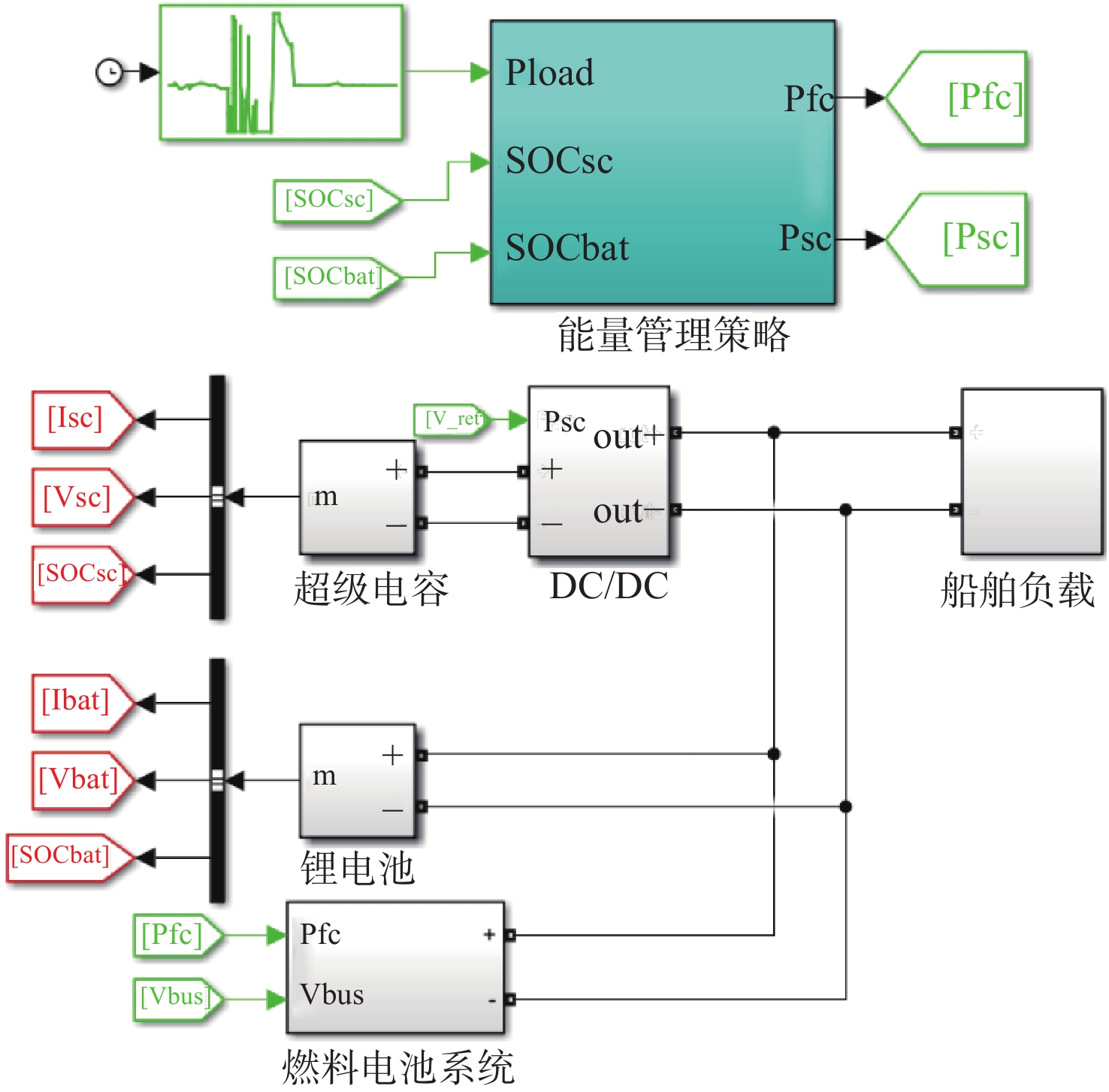
船舶动力系统的Simulink仿真模型整体框架如图10所示，包括燃料电池系统、由锂电池和超级电容组成的复合储能系统、船舶典型工况负载以及能量管理策略等仿真模块。将目标船的功率需求、电池SOC和超级电容SOC作为输入信号，经动力系统评价模型和灰狼算法处理，将最终的参数优化结果重新导入至仿真模型中进行计算分析。

图  10  混合动力系统及控制策略的简化模型

Figure  10.  Simplified model of hybrid power system and control strategy

下载: 全尺寸图片 幻灯片

5.1   仿真实验一

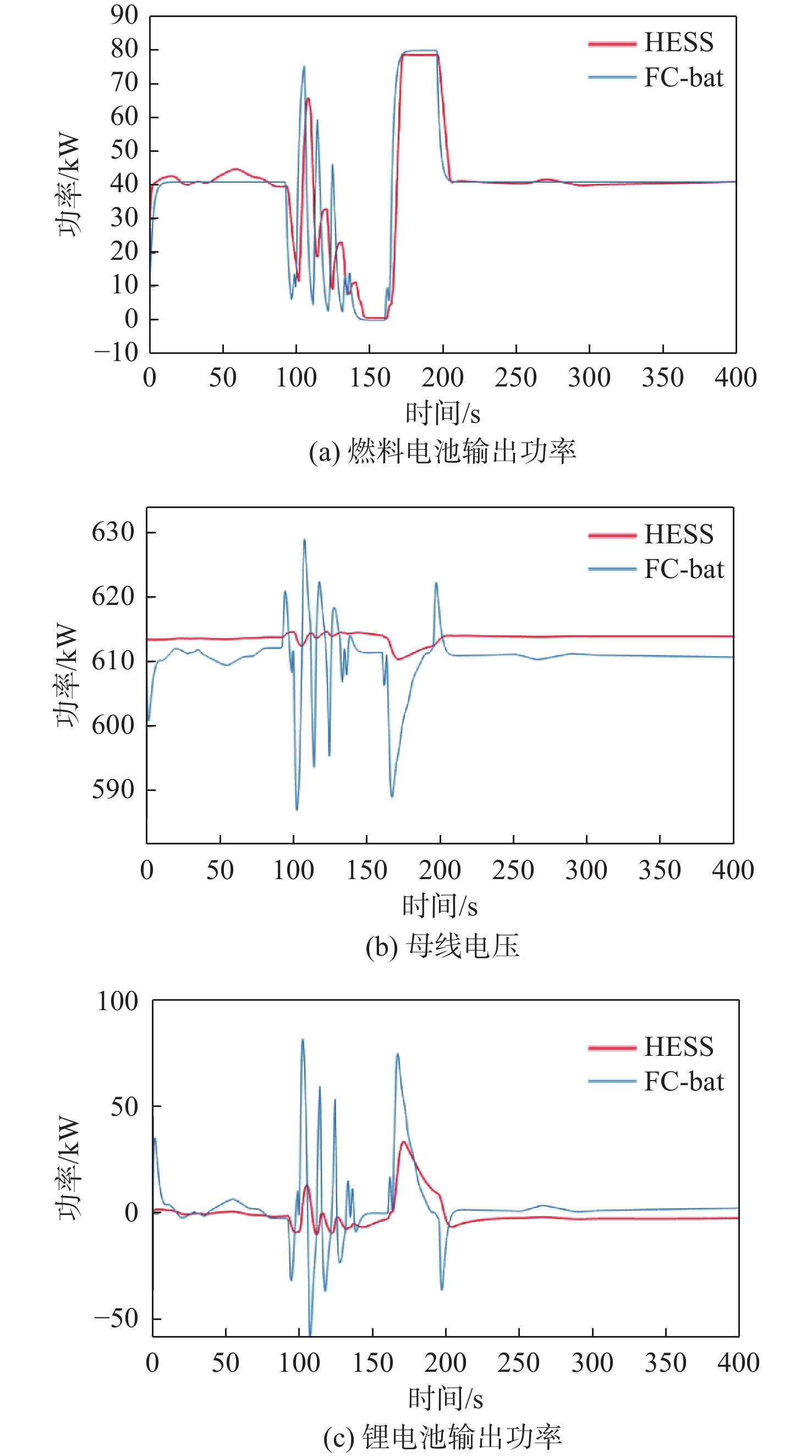
本节将在典型功率负载下，将本文提出的含复合储能的动力系统（HESS）与仅使用动力电池的原燃料电池船动力系统（FC-bat）进行对比。图11(a)为燃料电池的输出功率对比结果，在80～140 s区间，在本文控制策略的作用下，船舶机动状态下的燃料电池功率波动得以明显抑制。从图11 (b)可以看出，在船舶机动航行状态下，原船的母线电压波动和电压跌落更加显著，其中母线电压的最大波动差值高达41.3 V，而在本文策略下的母线电压波动则较为平缓，仅为5.3 V，因为超级电容及时承担了负荷扰动导致的高频分量，从而改善了船舶电能质量。图11 (c)为电池功率的对比结果，与原船铅酸蓄电池相比，采用超级电容后的锂电池输出功率更为平缓，其充放电功率的波动幅值降低了56%，有效改善了电池的充放电状态。

图  11  复合储能动力系统与仅使用动力电池的原燃料电池船动力系统的仿真结果对比

Figure  11.  Comparison of simulation results between composite energy storage power system with the original ship using only power batteries

下载: 全尺寸图片 幻灯片

5.2   仿真实验二

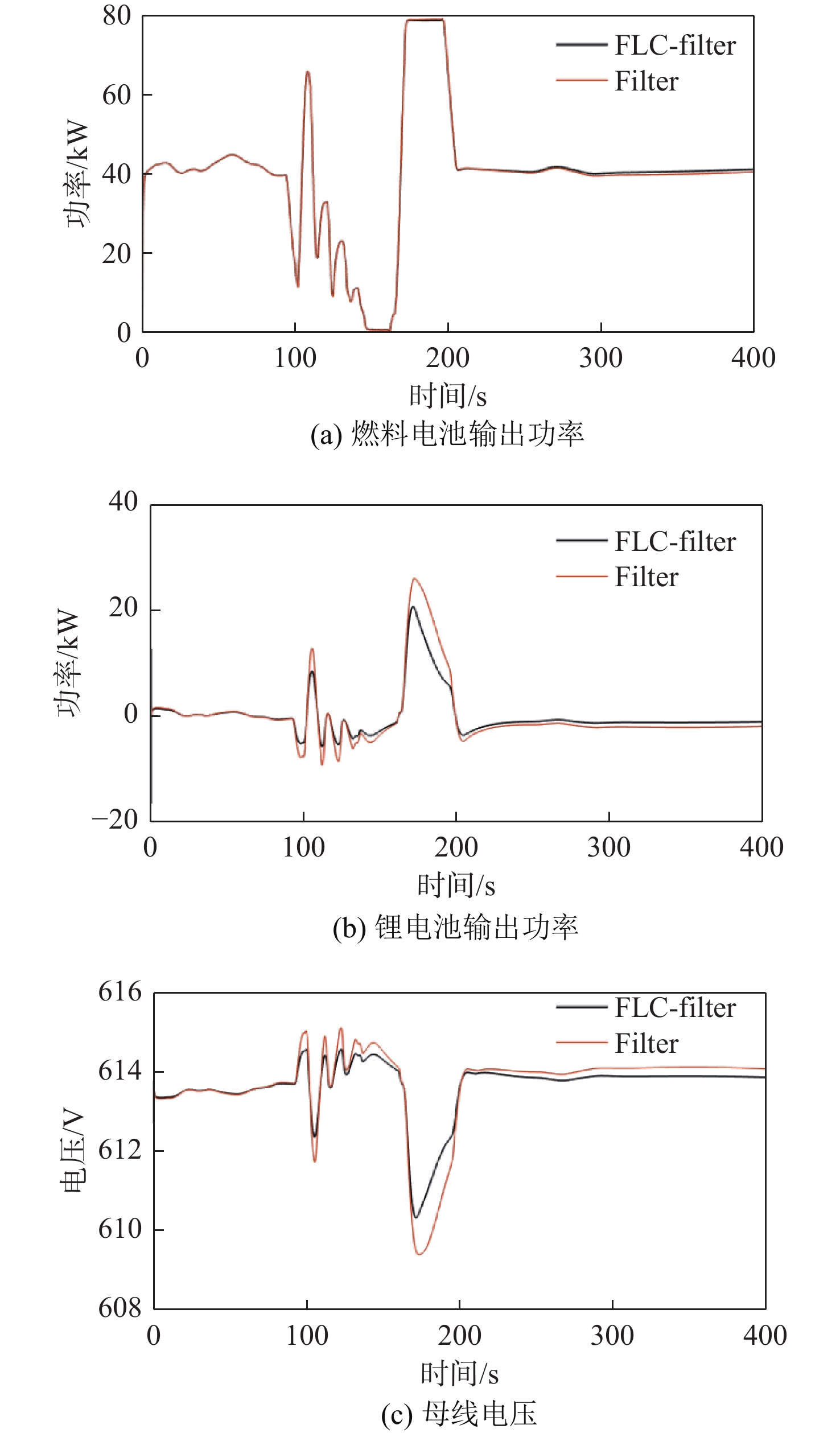
本节将在动力系统各参数相同的情况下，将复合储能系统能量管理策略FLC-Filter与不同的复合储能系统控制策略Filter进行对比，结果如图12所示，其中Filter控制策略即直接选用固定滤波器对复合储能系统的功率需求进行滤波处理。由图12 (a)可知，2种策略对燃料电池输出功率的影响差别较小；图12 (b)和图12 (c)的仿真结果表明，当船舶负载波动剧烈时，本文策略对于抑制锂电池输出功率波动、稳定母线电压方面的效果更好，经优化后的母线电压波动降低了23.19%，其在很大程度上发挥了超级电容短时输出功率高的优点。

图  12  不同控制策略下的仿真结果对比

Figure  12.  Comparison of simulation results under different control strategies

下载: 全尺寸图片 幻灯片

5.3   仿真实验三

鉴于复合电源系统在复杂工况中承担了较高频率的功率波动，本节将考虑电池或超级电容电量的极端情况，分别对复合电源SOC过高或过低的情况进行仿真实验，以验证能量管理策略对复合电源设备的保护能力。

5.3.1   工况一

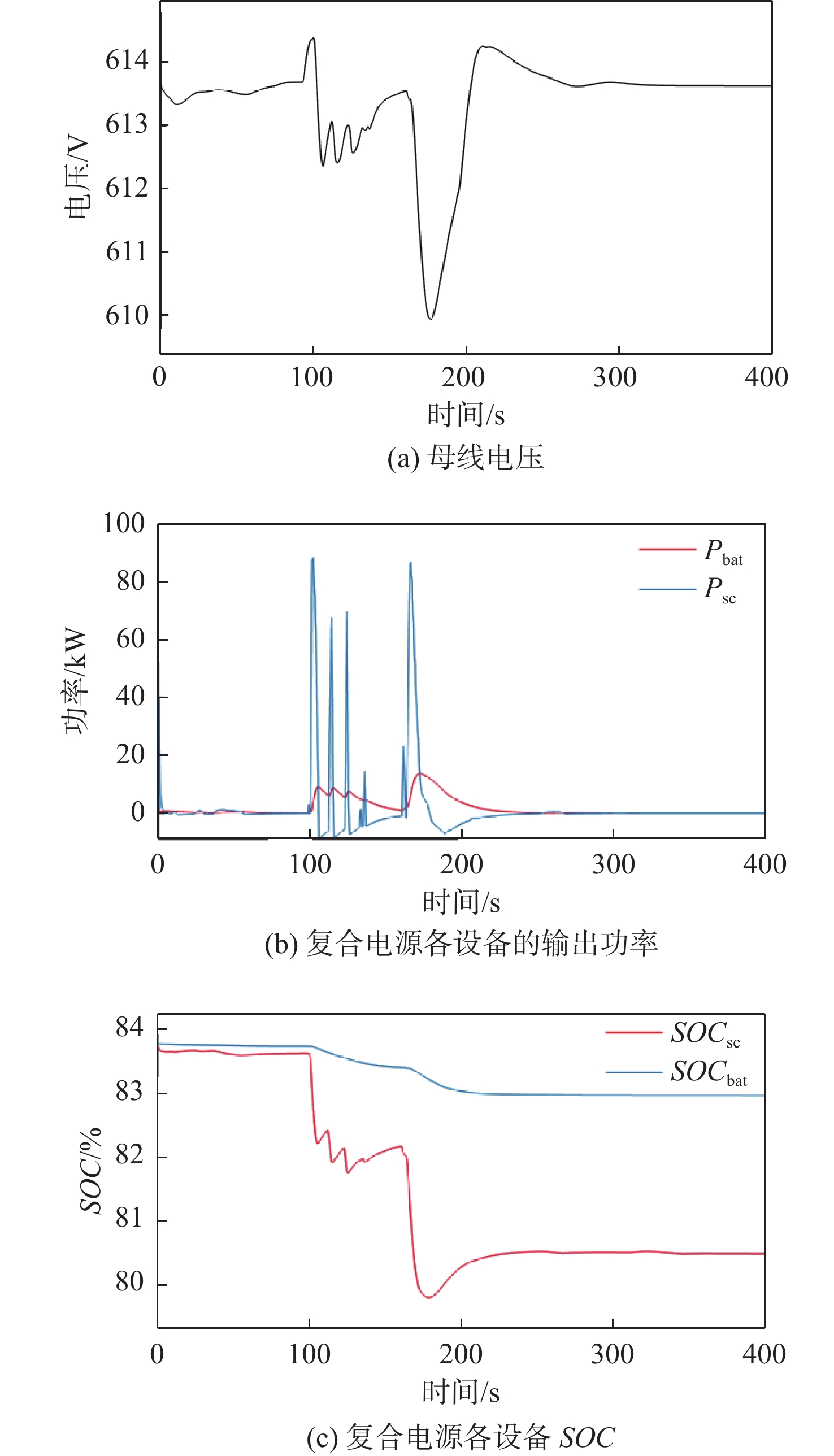
假定电池和超级电容的初始SOC均过高，分别设置为83.8%和83.6%。如图13所示，当复合电源SOC过高时，各设备均进行放电操作，以避免复合电源设备的过度充电，从而有效保护电源的健康状态，其中超级电容可通过自身进行快速放电。由图13(a)可知，母线电压的最大波动基本保持在5 V左右，因此，在本文控制策略下，复合电源并未因SOC过高而出现母线电压失稳的问题。

图  13  复合电源电量过高时的仿真结果

Figure  13.  Simulation results when the battery level of the composite power supply is too high

下载: 全尺寸图片 幻灯片

5.3.2   工况二

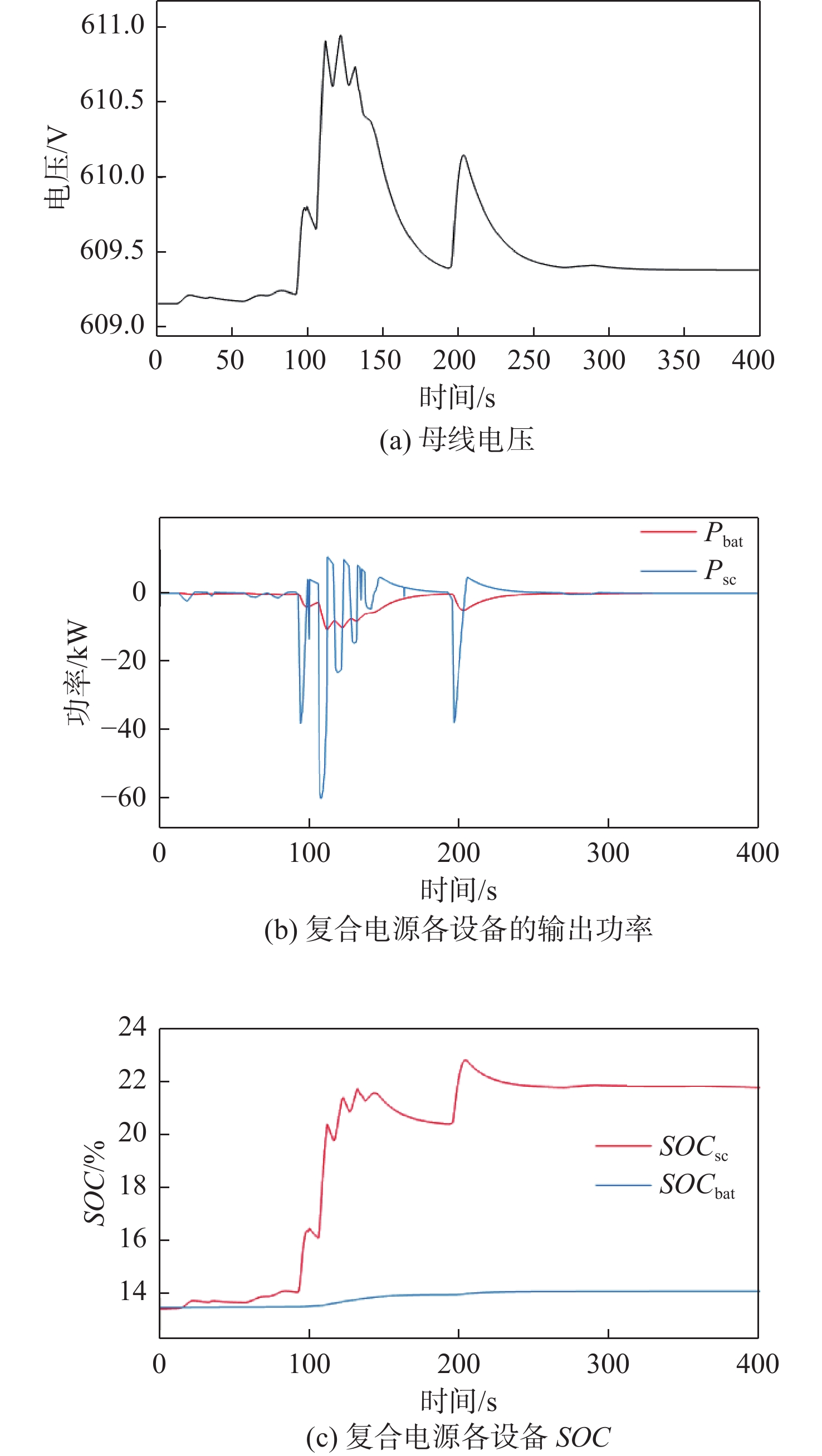
假定电池和超级电容的初始SOC均过低，均设置为13.4%。从图14可以看出，电池和超级电容的电量均不足时，整个复合电源系统将实施降功率工作，以避免设备过度放电；同时，各设备将进行充电操作，从而有效保护复合电源。

图  14  复合电源电量过低时的仿真结果

Figure  14.  Simulation results when the battery level of the composite power supply is too low

下载: 全尺寸图片 幻灯片

6.   结　语

针对复杂工况下船舶需求功率波动对直流电力系统的不良影响，本文基于电池—超级电容作为燃料电池船的复合储能系统，提出了一种考虑船舶运行工况的能量管理策略。该策略采用小波分解和模糊逻辑控制对船舶功率信号进行能量管理，基于能量平衡建立复合储能控制策略模型并建立优化目标函数，进而采用灰狼算法对燃料电池混合动力系统的能量管理策略参数和容量参数进行优化；在此基础上，在Matlab/Simulink环境下对混合动力系统进行建模，针对典型船舶工况进行仿真模拟实验，结果表明：对于由超级电容和锂电池组成的复合电源，超级电容承担了更高频的功率负载，并可维持锂电池更长时间的稳定输出；本文的能量管理策略可以有效抑制燃料电池的输出功率波动，可以在船舶复杂工况下稳定母线电压，从而提高电能质量，相较于Filter控制策略，优化后的母线电压波动降低了23.19%；同时，复合储能系统在机动工况下的充放电过程得以优化，有利于延长设备的使用寿命。需注意的是，本文主要研究了复合储能系统的控制策略，故对燃料电池的分析过于简单，后续将进一步优化能量管理策略。