Numerical analysis of bubble coalescence characteristics on wetting surface
-
摘要:目的
旨在促进超疏水表面与气泡复合减阻技术的发展，研究润湿性表面气泡的融合特性，揭示表面润湿性、气泡间距和气泡尺寸对气泡融合特性的影响规律。
方法基于流体体积（VOF）方法，建立水下润湿性表面气泡融合的数值模型，分析不同润湿性表面上气泡的融合与铺展特性。通过改变表面接触角、气泡间距和气泡尺寸，研究其对气泡融合特性的影响。最后，将模拟结果与实验数据进行对比，验证模型的准确性。
结果研究结果表明，表面接触角的增大和气泡间距的减小有助于气泡的融合，而气泡尺寸的增大则会减缓气泡在表面的铺展速度，不利于气泡融合。具体而言，当表面接触角从130°增大到170°时，气泡开始融合的时间从5.6 ms缩短至3.2 ms，减少了42.9%；而气泡的最大铺展距离从6.53 mm增加至9.4 mm，提升了138%。
结论研究结果可为超疏水表面与气泡减阻技术的耦合设计提供理论依据。研究还表明，优化表面润湿性和气泡间距可以显著提升气泡融合效果，进而提高气泡减阻的稳定性和效率。
Abstract:ObjectiveThis study aims to advance the development of composite drag reduction technology involving super-hydrophobic surfaces and bubbles by investigating the coalescence characteristics of bubbles on wetting surfaces and revealing the effects of surface wettability, bubble spacing, and bubble size on bubble coalescence.
MethodsA numerical model of bubble coalescence on an underwater wetting surface is established based on the volume of fluid (VOF) method. The coalescence and spreading characteristics of bubbles on different wetting surfaces are analyzed by varying the surface contact angle, bubble spacing, and bubble size. The accuracy of the simulation results is validated by comparing them with experimental data.
ResultsThe results show that increasing the contact angle of the wetting surface and decreasing bubble spacing facilitate bubble coalescence, while increasing bubble size slows down the spreading speed of bubbles on the surface and is not conducive to accelerating bubble coalescence. Specifically, when the contact angle increases from 130° to 170°, the initial coalescence time of bubbles decreases from 5.6 ms to 3.2 ms (a reduction of 42.9%), and the maximum spreading distance of bubbles increases from 6.53 mm to 9.4 mm (an increase of 138%).
ConclusionsThe findings provide a theoretical basis for the coupling design of super-hydrophobic surfaces and bubble drag reduction technology. Optimizing surface wettability and bubble spacing can significantly enhance bubble coalescence, thereby improving the stability and efficiency of bubble drag reduction.
-
0. 引 言
长期以来，气泡减阻一直是船舶减阻领域的研究热点[1-2]。对于船舶气泡减阻而言，气泡在船底表面快速融合形成气层并稳定附着是维持气泡减阻效果的重要保障[3-4]。然而，实船航行时水下环境复杂，对于气泡融合与铺展特性的研究尚不充分，气泡减阻的稳定性仍然面临很大挑战。因此，如何优化气泡的融合与铺展特性，成为提升气泡减阻稳定性的关键。
超疏水表面在水下具有“超亲气”性质[5]，有望改善气泡的融合特性，提升船舶减阻效果。有学者曾尝试利用超疏水表面提高气泡在船底的附着能力，在船底大面积使用疏水表面进行气泡减阻试验，试验取得了较好的结果。Fukuda等[6]利用超疏水表面对气泡的吸引特性，尝试减缓船底气泡的扩散，取得明显效果。Latorre等[7]对使用超疏水涂层双体船模表面进行了气泡减阻试验，结果表明，气泡减阻效果明显，其中，涂层产生了4%～6%的阻力减额，涂层上的气泡减少了4%～11%的总阻力。然而，上述试验仅从减阻效果角度印证了超疏水表面有利于气泡减阻效果的提升，且仅停留在宏观层面，未关注超疏水表面对气泡铺展和融合行为的作用机理，气泡减阻的稳定性仍未得到充分保障，无法为超疏水表面与气泡复合减阻技术提供坚实的理论基础。
为进一步明确表面润湿性影响气泡运动特性的规律，有许多学者针对单个气泡进行了研究。例如，Kitagawa[8]等采用跟踪测速法研究了润湿性对沿壁上升的微米级氢气泡黏附行为的影响，发现沿疏水壁面上升的气泡可以很快附着在壁面上，而沿着亲水以及超亲水壁面上升的气泡不能发生黏附，这再次印证了低润湿性的疏水表面能够提高水下气泡的附着能力。叶煜航等[9]采用高速阴影成像系统研究气泡在超疏水轨道上的运动特性，结果表明，壁面浸润性分布和惯性力的耦合效应可以改变气泡的移动速度和稳定性；Kim和Lee[10]采用流体体积（VOF）法的多相流模型研究了表面润湿性对气泡与固体表面相互作用规律的影响，发现运动的气泡与亲水表面作用后会发生弹跳，而与疏水表面作用后发生吸附，当接触角大于110°时气泡在表面铺展；其后，唐子建等[11]在上述基础上考虑固体壁面的曲度，采用实验方法得到了相同结论。此外，胡海豹等[12]将亲水表面和疏水表面进行组合排列，在表面形成润湿阶跃来提高厘米级气泡的稳定性。孙远志等[13]对微结构表面上的单气泡运动特性进行数值模拟，分析了气泡的脱离周期、体积膨胀率等指标，揭示了表面润湿性对气泡动力学特性的影响规律。综上所述，现有研究大多集中于不同润湿性表面上单气泡的运动规律，然而在气泡减阻技术中，多气泡融合现象普遍存在。因此，研究不同润湿性表面上的气泡融合和铺展特性更具价值。
为了推动超疏水表面与气泡复合减阻技术的发展，迫切需要开展润湿性表面与气泡减阻技术相结合的研究，深入探索气泡融合及铺展特性。由于船舶气泡减阻技术所涉及的气泡尺寸较小，且气泡融合过程发生时间极短，通过实验观察存在一定困难。鉴于此，本文将采用数值模拟方法，建立一个接近实际情况的有重力环境，综合考虑接触角、气泡间距和气泡尺寸等因素的影响，分析气泡在润湿性表面上的融合特性。
1. 模型及方法
1.1 流体体积模型
本文对于不同润湿性表面气泡融合的研究属于典型的多相流问题。流体体积（VOF）模型能够较好地追踪多种不相溶流体的交界面，从而准确地求解多相流问题。
不可压缩牛顿流体的质量守恒方程和动量守恒方程为
∇⋅u=0 (1) \frac{\partial\left(\rho u\right)}{\partial t}+\rho\left(u\nabla u\right)=\nabla\left[\mu\left(\nabla u+\nabla {{\boldsymbol{u}}}^{\mathrm{T}}\right)\right]+F_{\rm{s}}+\rho\boldsymbol{g}-\nabla p (2) 式中：g为重力加速度；p为压强；u为速度； F_{\rm{s}} 为表面张力； \rho 为平均密度； \mu 为平均动力黏度。
VOF模型是基于流体体积进行求解的，气液两相的体积分数输运方程如下：
\frac{{\delta {\alpha _{\rm{v}}}}}{{\delta t}} + \nabla \left( {{\alpha _{\rm{v}}}{u_{\rm{v}}}} \right) = 0 (3) \frac{{\delta {\alpha _{\text{l}}}}}{{\delta t}} + \nabla \left( {{\alpha _{\rm{l}}}{u_{\rm{l}}}} \right) = 0 (4) 式中： {\alpha _{\text{v}}} 为气相体积分数； {\alpha _{\text{l}}} 为液相体积分数； {\rho _{\text{v}}} 和 {\rho _{\text{l}}} 分别为气相和液相的密度； {u_{\text{v}}} 和 {u_{\text{l}}} 分别为气相和液相的速度；t为时间。
{\alpha _{\text{v}}} 和 {\alpha _{\text{l}}} 的取值均在[ 0, 1]区间内，表征网格内气相和液相的体积分数，并在每一个计算网格内始终存在以下关系：
{\alpha _{\text{v}}} + {\alpha _{\text{l}}} = 1 (5) 对于多相流计算网格中平均密度 \rho 和平均动力黏度 \mu ，通过下式求解。
\rho = {\alpha _{\text{v}}}{\rho _{\text{v}}} + {\alpha _{\text{l}}}{\rho _{\text{l}}} (6) \mu = {\alpha _{\text{v}}}{\mu _{\text{v}}} + {\alpha _{\text{l}}}{\mu _{\text{l}}} (7) 式中， {\mu _{\text{v}}} 和 {\mu _{\text{l}}} 分别为气相和液相的动力黏度。
表面张力在多相流问题中起着重要作用。本文所采用的VOF表面张力模型是CSF 模型（continuum surface force model），其最早由Brackbill等[14]提出。在气液两相流中，表面张力表达式为
{F_{\rm{s}}} = 2\gamma \rho k\nabla {\alpha _{\rm{l}}}/\left( {{\rho _{\rm{v}}} + {\rho _{\rm{l}}}} \right) (8) 式中： \gamma 为表面张力系数；k为界面的曲率。
通过式（9）求解厄特沃什数 Eo 。
Eo=\rho_{\text{l}}\boldsymbol{g}r^2/\gamma (9) 式中， r为气泡半径。
1.2 数值验证
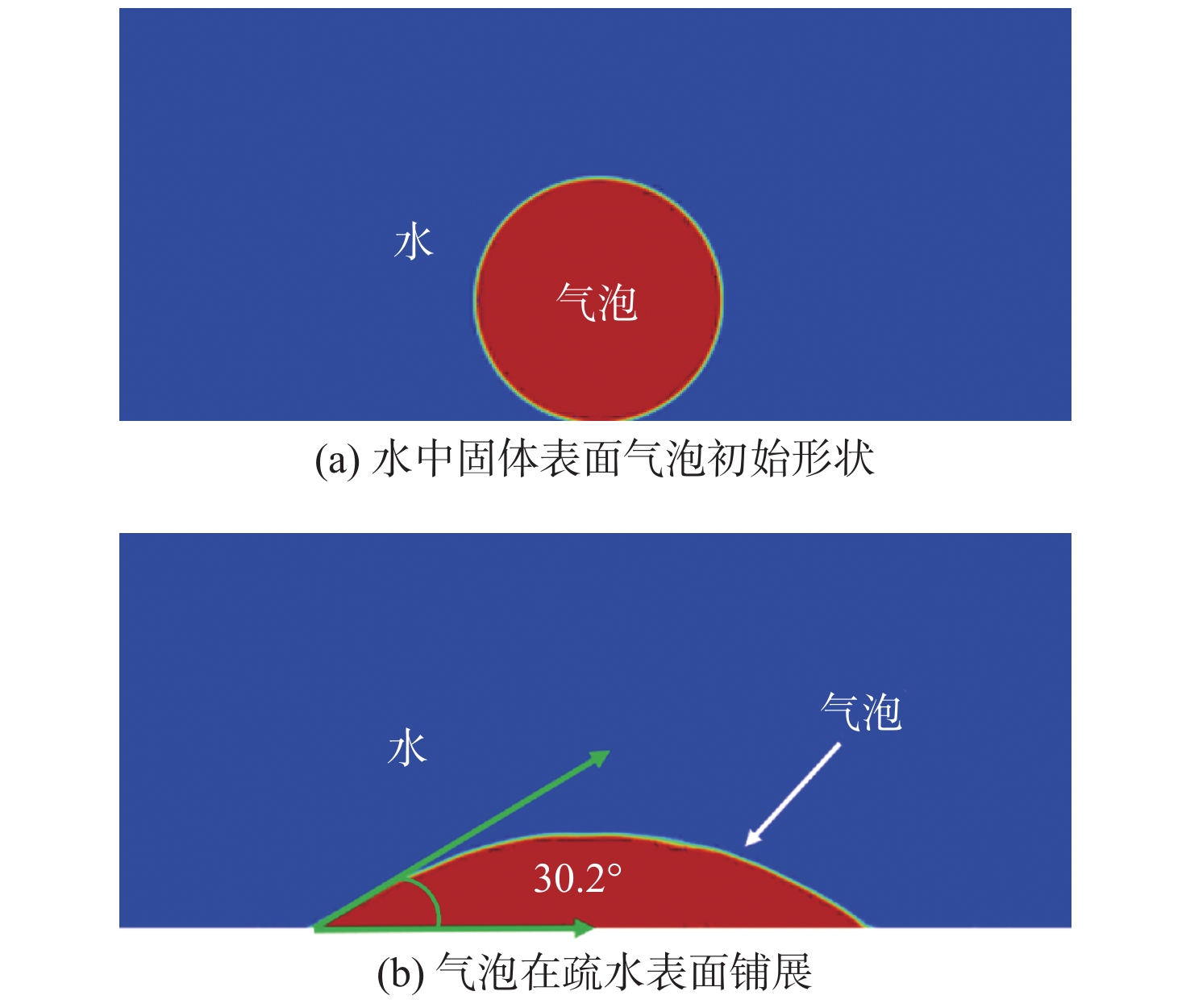
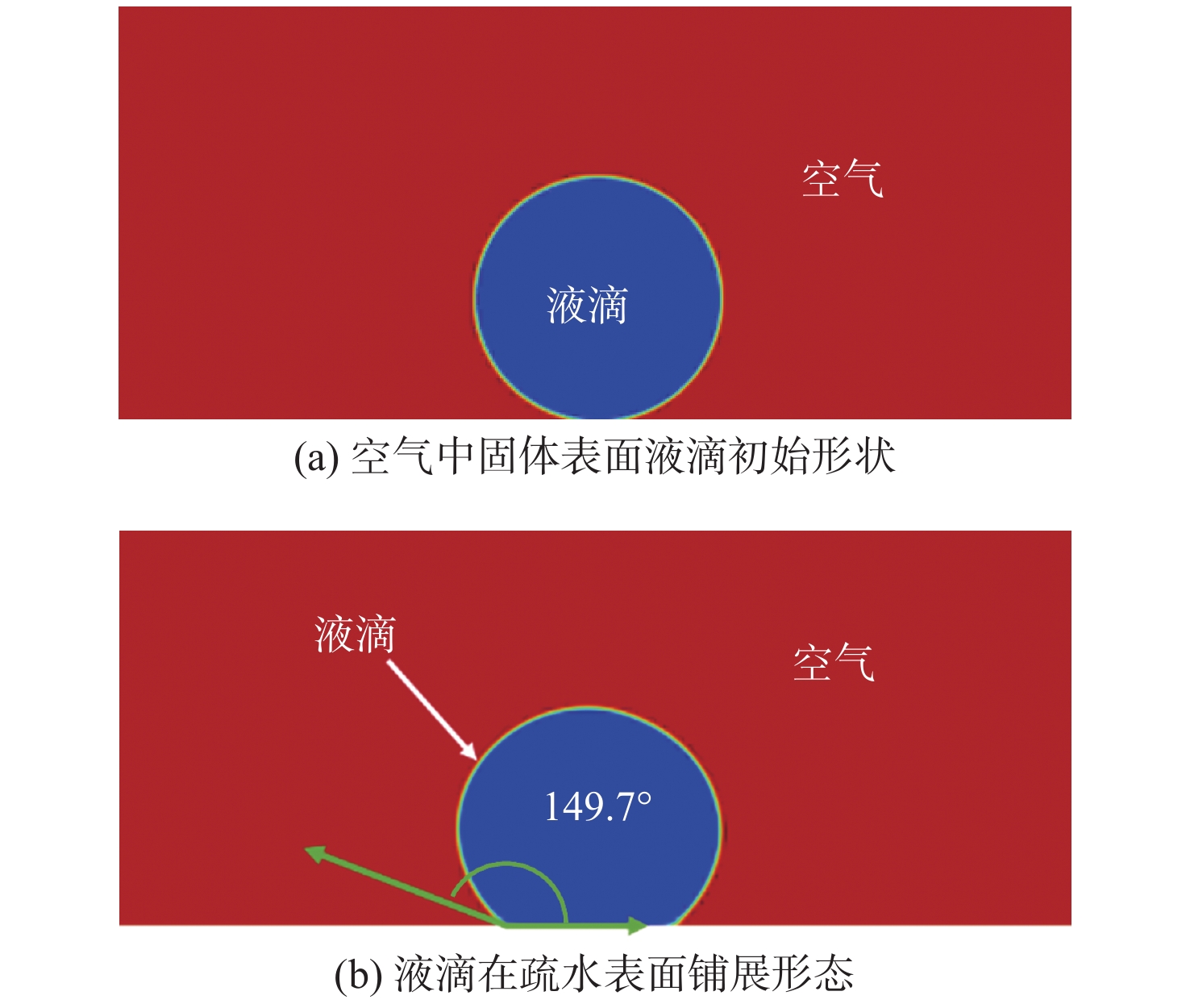
为了验证所选模型在研究中的适用性和可靠性，本文采用Ansys Fluent 2021软件进行数值仿真，分别针对空气环境中液滴在固体表面的浸润问题（图1）和水中气泡在固体表面的铺展问题（图2）进行模拟。在模拟过程中，设置初始条件如下：液滴和气泡半径r均为1 mm，且位于计算域底部正中心；底部为无滑移壁面，且表面接触角 {\theta _{\rm{CA}}} = 150°。通过开启壁面黏附作用Wall Adhesion模型调节表面接触角。气液表面张力系数 \gamma = 0.073 N/m。基于上述初始条件，模拟表面接触角 {\theta _{{\text{CA}}}} = 150°时超疏水壁面上的润湿现象。
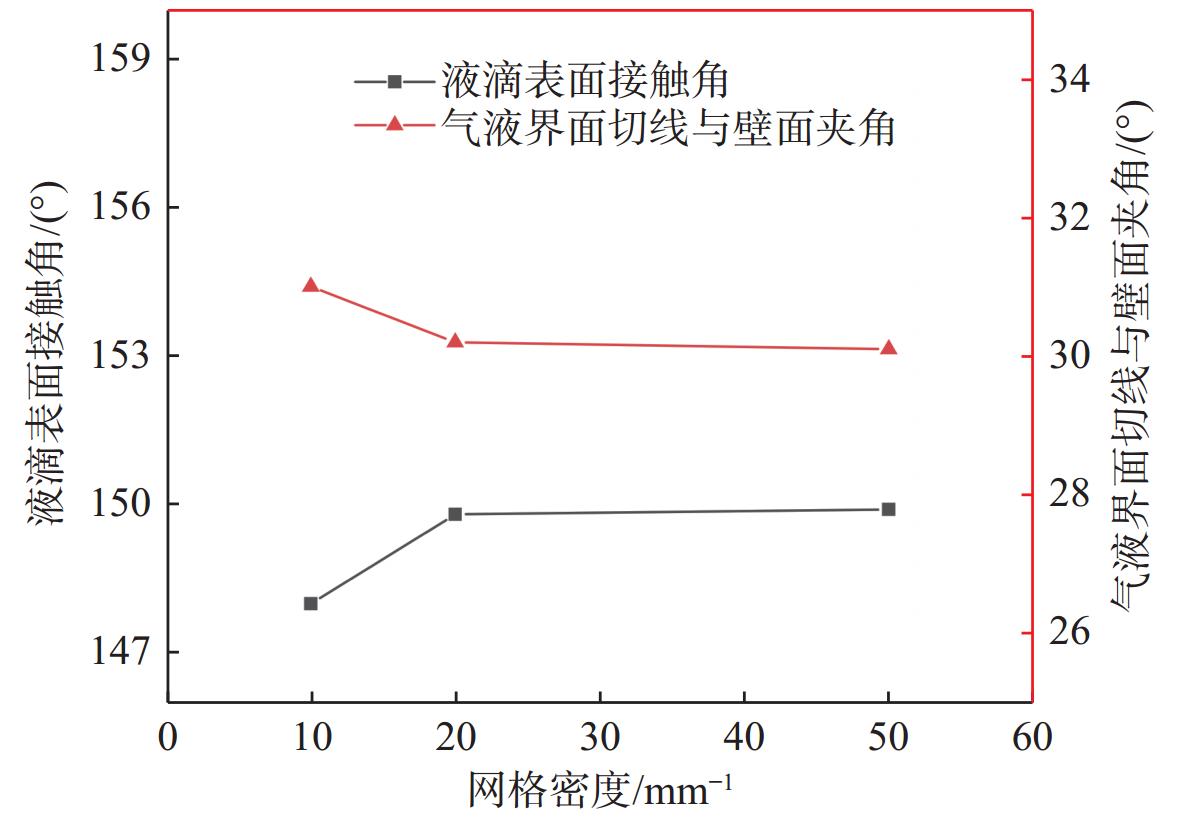
在网格无关性验证时， 设网格密度 N = 1/\Delta x （ \Delta x 为网格尺寸）。为排除网格因素对结果的影响，本文研究中共采用3种网格方案（ N = 10 ， N = 20 ， N = 50 ）计算空气环境中液滴在固体表面的浸润和水中气泡在固体表面的铺展这两个问题，结果如图3所示。
由图3可以看出，在 N = 20 时，计算结果收敛，对应的网格尺寸 \Delta x = 1/N = 0.05 ，故该验证算例采用0.05 mm尺寸的网格符合计算要求。此时，网格最大纵横比为2，全局网格的质量均超过0.9。
根据液滴的静态接触角模拟结果，如图1（b）所示，液滴形状稳定后测得其接触角为149.7°，其与预设值之间的误差仅0.2%。同样地，对水中气泡在固体表面的铺展情况也进行了模拟，最终结果如图2（b）所示。超疏水意味着超亲气，水下气液交界面的切线与固体壁面的夹角 {\theta _{}} 和表面接触角 {\theta _{\rm{CA}}} 彼此是互补的[15]，当 {\theta _{\rm{CA}}} = 150^\circ 时， \theta = 30^\circ 。在气液交界面基本稳定时，测得的气液交界面的切线与固体壁面的夹角 \theta = 30.2°，其与预设值间的误差仅为0.7%，且仍处于允许的范围内。
为进一步验证模型的准确性，本文选取液体中竖直方向的气泡融合过程进行模拟。其中，厄特沃什数 Eo = 4，液体密度为
1267 kg/m3，动力黏度为2.306 Pa/s，表面张力系数为0.0705 N/m。图4所示的黑白区域气泡形状为实验结果，红色气泡形状为仿真结果。通过对比可知，仿真结果与试验结果[16]基本一致。![]()
图 4 气泡靠近和融合过程与实验结果（黑白图片所示[16]）对比Figure 4. Comparison of bubble approach and coalescing process with experimental results indicated by grey images[16]上述算例的结果表明，本文使用的接触角模型能够准确地描述壁面润湿性，表面张力模型的作用也可精确地体现表面张力的作用，而VOF多相流模型能够较好地捕捉疏水表面气泡的铺展现象。鉴于此，本文采用了VOF多相流模型和壁面黏附作用Wall Adhesion模型来研究不同润湿性表面气泡融合和铺展问题。
1.3 几何模型和计算设置
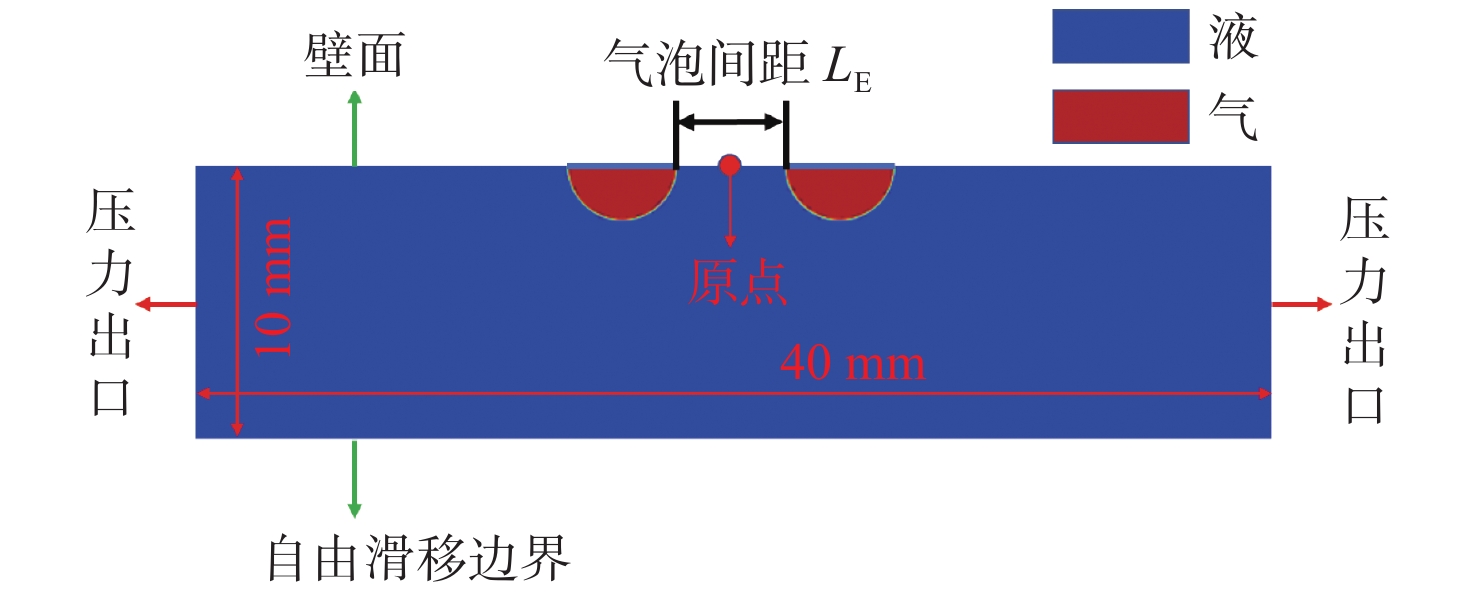
图5所示为本文数值计算采用的几何模型。其中，计算域长度为40 mm，高度为10 mm；流场下边界为自由滑移边界，表示流场下边界不对结果产生影响[17-18]；上壁面为疏水壁面，研究中通过改变上壁面的表面接触角 {\theta _{\rm{CA}}} 来调节气泡在壁面上的润湿行为；原点位于上壁面中心，气泡位于图中所示原点的两侧，且初始形状为半圆形。为了模拟接近气泡减阻的真实情况，研究中考虑了重力的影响，具体而言，重力在y轴方向的大小为−9.81 m/s2。由图可见，上壁面为船底表面，气泡附着在壁面上，气泡间距为 LE。为更好地进行定性与定量分析，除非特别说明，本文研究中所设置的气泡半径均为r = R = 1 mm，直径均为d = D = 2 mm，此处使用的R和D分别表示气泡半径和直径的这一特定取值。
如图6所示，流体域网格均采用结构化网格，气泡运动的上半区网格予以加密，经网格无关性验证后，网格尺寸取0.05 mm，以便更精准地捕捉气液交界面。气液表面张力系数取为0.073 N/m[19]，即约20 °C时水的表面张力系数，并开启壁面黏附作用Wall Adhesion模型来调节表面接触角。同时，计算采用了Laminar层流模型、PISO（pressure implicit with splitting of operators）压力和速度求解方法，时间步长取1×10−5 s。
2. 结果分析
首先，模拟相同气泡之间的融合过程，探究表面润湿性对气泡融合和铺展的影响；然后，在此基础上研究气泡间距的影响规律；最后，分析气泡尺寸对气泡之间的融合和铺展特性的影响。
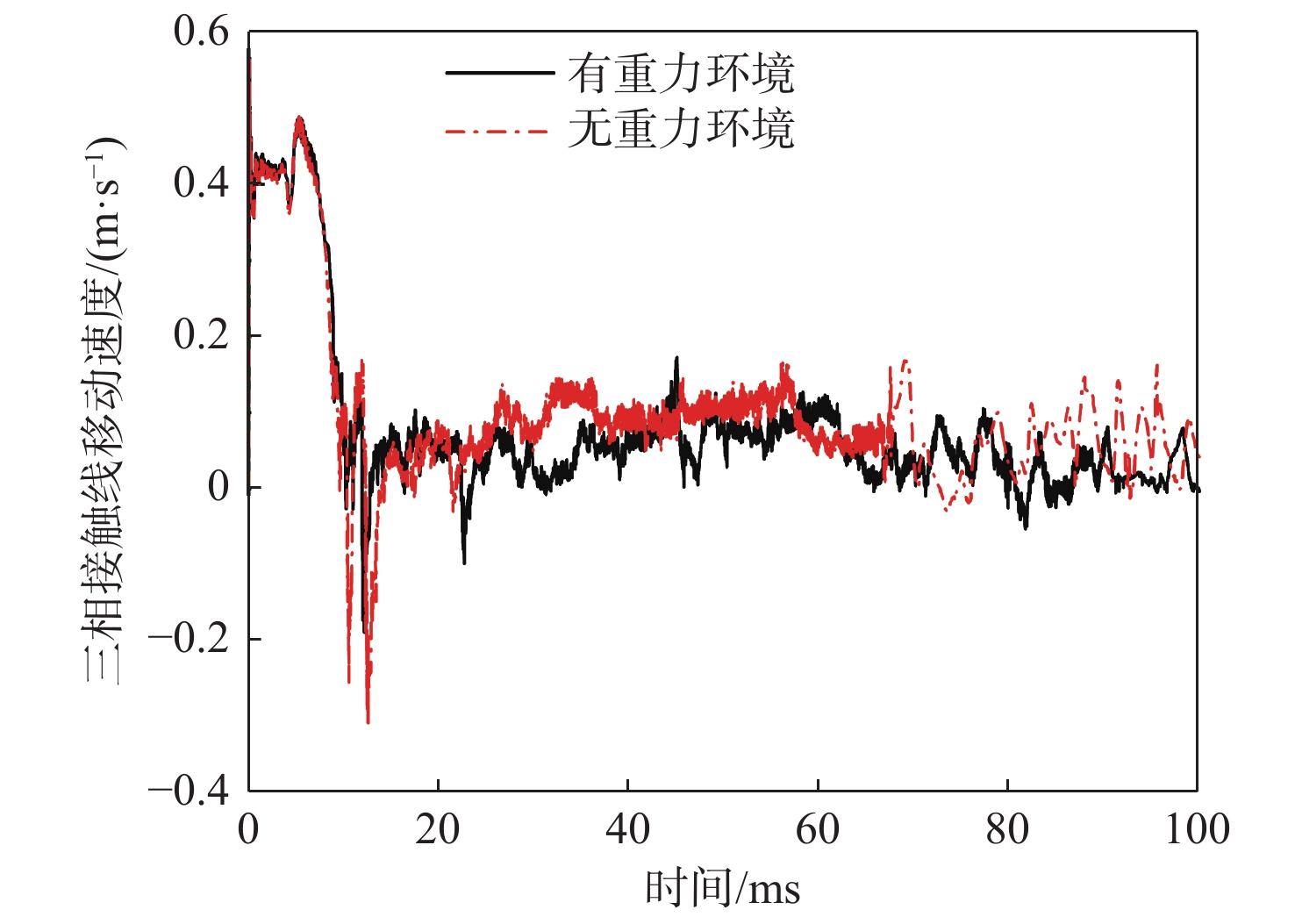
为量化地描述气泡的铺展特性，令气泡铺展速度 {v_{\text{s}}} = {L_{\rm{E}}}/{t_{\text{c}}} （ {t_{\text{c}}} 为气泡开始融合时间）。与之相应的，接触线移动速度是指接触线移动的距离与所需时间的比值。为验证重力对气泡融合的影响，首先对比分析有/无重力这两种条件下气泡在固体表面接触线的移动速度，结果如图7所示。
由图7可见，在0～10 ms范围内，重力对三相接触线速度的影响很小，此时该速度由壁面黏附力主导，但12 ms后，两者的速度差异逐渐凸显，说明重力的存在会影响气泡在壁面上的铺展速度，并一定程度上影响 了气泡融合特性，因此考虑重力的作用是有必要的。韩蕊[20]在自由流场气泡融合研究中分析了重力影响，得到了与本文相同的结论。
2.1 表面润湿性对气泡融合的影响
表面润湿性直接影响了气泡在固体表面上的铺展形态，是影响船底表面气泡之间融合的关键因素。表面润湿性由表面接触角 {\theta _{\rm{CA}}} 来表征[21]。本节中，2个相同尺寸的气泡间距取 {L_{\rm{E}}} = D ，表面接触角 {\theta _{\rm{CA}}} 取值范围为130°～170°。基于此研究气泡在不同润湿性表面的融合和铺展特性。
2.1.1 不同润湿表面气泡的融合过程
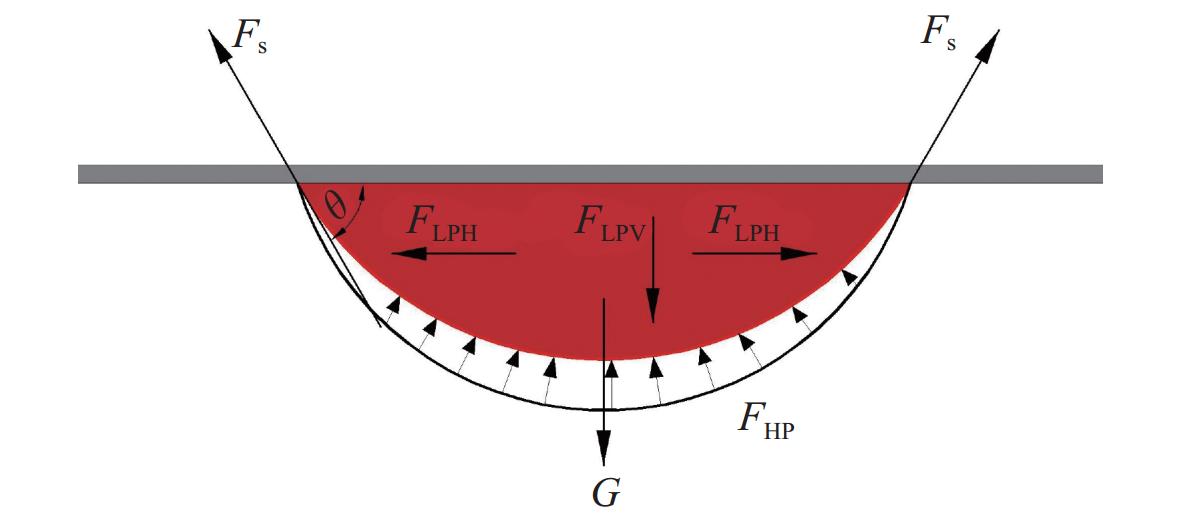
如图8所示，水下壁面上气泡受到多种力的作用。在气泡静止时受到的作用力包括重力G、静水压力 {F_{\rm{HP}}} 和壁面法向力等外力，以及气泡表面张力 {F_{\rm{s}}} 和Laplace应力 {F_{\rm{LP}}} 等内力。
拉普拉斯应力方程如下：
{F_{\rm{LP}}} = \Delta p = \gamma /{R_1} (10) 式中： \Delta p 为液体内外压强差； {R_1} 为气液交界面曲率半径。 {F_{\rm{LP}}} 在水平方向的分力表示为 {F_{\rm{LPH}}} ，在垂直方向的分力表示为 {F_{\rm{LPV}}} 。
结合Kibar等[22]和叶煜航等[23]的研究可知，当气泡铺展时，其还会额外地受到壁面的摩擦力、气泡自身的形状阻力、运动产生的黏性阻力和附加质量力等作用力的影响。下文将通过受力分析来研究水下气泡的运动及其铺展特性。当气泡半径 r = 1 mm时，本文选取壁面气液接触角 {\theta _{\rm{CA}}} = 170^\circ 和 {\theta _{\rm{CA}}} = 130^\circ 这两种典型工况对表面气泡之间的融合过程进行分析。
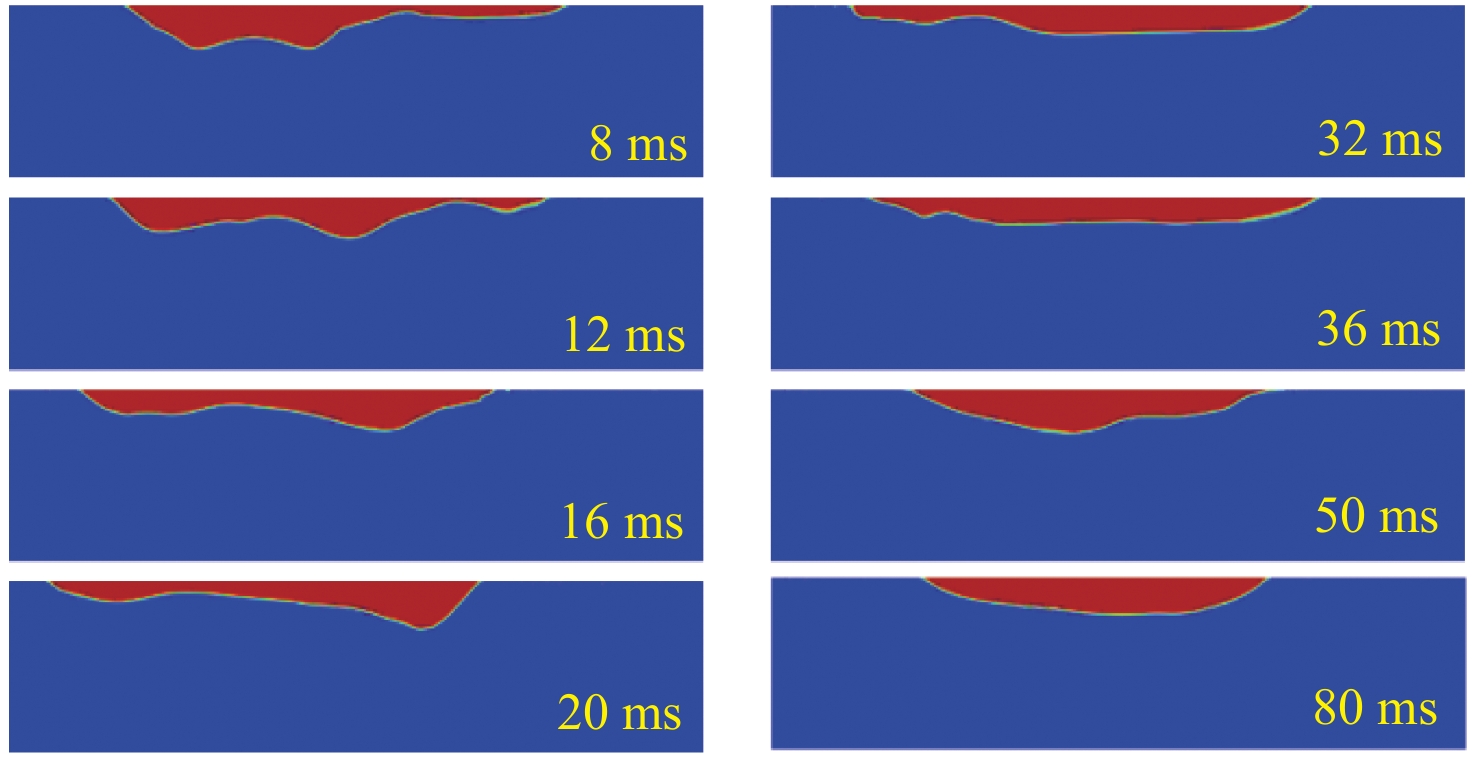
1） {\theta _{\rm{CA}}} = 170^\circ 时表面气泡之间的融合过程。
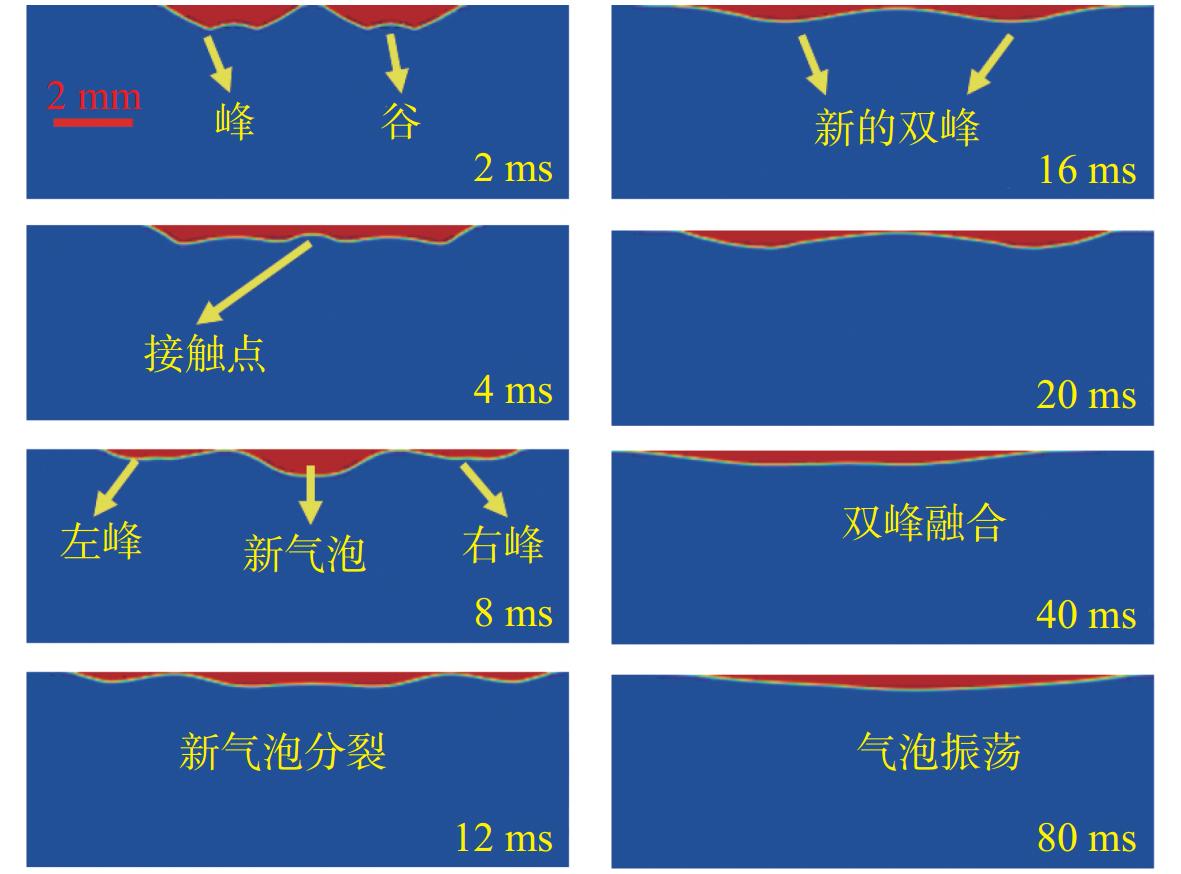
由图9所示壁面气泡之间的融合过程计算结果可见，气泡的融合过程大致分为5个阶段：
![]()
图 9 表面接触角为170°时的气泡融合过程Figure 9. Coalescing process of bubbles at a contact angle of 170°（1） 气泡铺展。在0～4 ms时间段，在壁面黏附力的作用下，移动接触线逐渐沿着壁面向外移动，这与Kim和Lee[10]观察到的现象一致，即气泡在疏水壁面上直接铺展。同时，在静水压力 {F_{\rm{HP}}} 的作用下，气泡顶端从自身对称中心处开始塌陷，这一现象在Kumar等[19]和朱智成[24]的研究中也有所体现，也即气泡底部中心位置在浮力作用下凹陷，此时气泡开始形成“双峰”形状，且“双峰”高度逐渐降低而“谷”逐渐变宽。气泡融合前的运动类似于单气泡在壁面上的铺展过程，此时“双峰”是关于该气泡中心对称的。然而，随着气泡开始靠近，气泡在表面张力 {F_{\rm{s}}} 作用下开始相互吸引。
（2） 气泡初步接触。在4～8 ms时间段，此时气泡之间的液膜破裂。在表面张力 {F_{\rm{s}}} 的作用下，附近的气体迅速向接触区域汇聚，并以接触区域为中心重新形成新的弧形气泡。在韩蕊[20]以及Shaw和Deike[25]的自由液面气泡融合实验中也显示出了类似的结果。此外，由于气泡的表面张力 {F_{\rm{s}}} 以及静水压力 {F_{\rm{HP}}} 的作用，左气泡的“左峰”和右气泡的“右峰”气液界面变得平缓。最终，整个气泡聚合形成“山”字形态，左右两侧为小的弧形气泡，中间为稍大的弧形气泡，气泡底部联通。
（3） 气泡逐步融合。约在8～20 ms时间段，气泡在形成“山”字分布后开始进一步融合。在静水压力 {F_{\rm{HP}}} 和壁面黏附力的作用下，中间大气泡从自身对称中心处开始塌陷，两侧小气泡直接与大气泡分裂的气体融合，并在铺展到极限后开始回缩，此时“山”字形态的气泡完全演化为新的“双峰”形状。
（4） 气泡完全融合。约在20～40 ms时间段，在气泡形成新的“双峰”状后，由于气泡的铺展程度较大，气泡厚度较小，呈扁平状，此时气泡的界面靠近壁面，其受到的静水压力 {F_{\rm{HP}}} 较小，且并未像在气泡铺展阶段从气泡对称中心处开始塌陷。此时，壁面黏附力小于表面张力的水平分量，气泡进入收缩阶段，“双峰”体积向气泡接触区域汇聚，最后形成一个整体，同时气泡移动接触线开始收缩。
（5） 气泡振荡。气泡融合后形成的大气泡在惯性力、表面张力 {F_{\rm{s}}} 、壁面支持力以及静水压力 {F_{\rm{HP}}} 的作用下开始振荡，此时气泡的厚度和铺展范围开始呈现规律性的变化，气液界面也产生一定的波动。与自由液面气泡融合[25]以及自由流场气泡融合[26]后仅发生横向振荡不同，本文研究中气泡在重力作用下重心在竖直方向发生了明显位移，导致气泡融合后产生的振荡以竖直方向为主。最后，在流体阻力、附加质量力、壁面剪切力等作用影响下，气泡形态完全稳定。
2） {\theta _{\rm{CA}}} = 130^\circ 时表面气泡之间的融合过程。
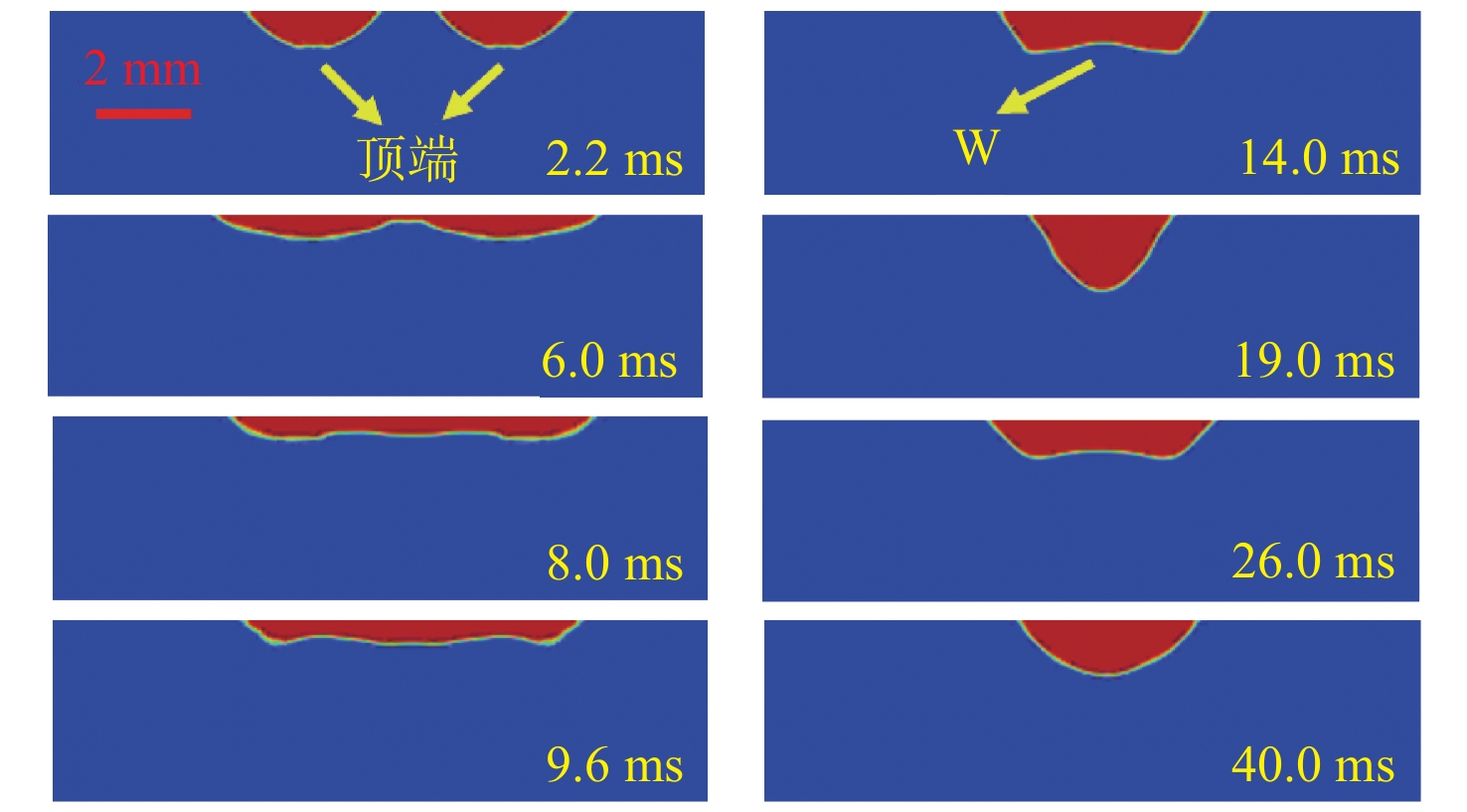
由图10所示壁面气泡之间融合过程的计算结果可见，与 {\theta _{\rm{CA}}} = 170^\circ 时的融合过程相比，二者略有差异，但大致趋势基本一致。具体而言：
![]()
图 10 表面接触角为130°时的气泡融合过程Figure 10. Coalescing process of bubbles at a contact angle of 130°（1） 气泡铺展。在0～6 ms时间段，气泡开始铺展，与 {\theta _{\rm{CA}}} = 170^\circ 时有所不同，气泡顶端并未出现明显的凹陷现象，整个气泡形状仍保持较好，类似圆台或弧形，直至气泡铺展后二者开始靠近并融合。与 {\theta _{\rm{CA}}} = 170^\circ 时的壁面黏附力相比， {\theta _{\rm{CA}}} = 130^\circ 时壁面黏附力较小，使得移动接触线变化速度较慢。此时，气泡的曲率半径较小，Laplace应力竖直方向分力 {F_{\rm{LPV}}} 较大，具备了抵抗静水压力 {F_{\rm{HP}}} 的能力。
（2） 气泡融合。在6～19 ms时间段，左边气泡的右半部和右边气泡的左半部向气泡接触区域汇聚。但 {\theta _{\rm{CA}}} = 130^\circ 时的气泡壁面黏附力比 {\theta _{\rm{CA}}} = 170^\circ 时的小得多，此时气泡移动接触线已开始回缩，且气泡开始聚拢形成“W”形状，最终形成弧形。气泡在融合过程中未形成明显的多峰形状。
（3） 气泡振荡。在19 ms后，气泡同样开始振荡，直至完全稳定。从表面接触角 {\theta _{\rm{CA}}} = 170^\circ 和 {\theta _{\rm{CA}}} = 130^\circ 时的气泡融合过程可知，该过程一般分为铺展、接触、融合和振荡等阶段，表面接触角对其壁面的气泡融合和铺展特性有着较为显著的影响，其中气泡的铺展和振荡过程受到的影响程度较大。 {\theta _{\rm{CA}}} = 170^\circ 时壁面气泡在融合前的铺展速度大于 {\theta _{\rm{CA}}} = 130^\circ 时的，且融合后的振荡时间及幅度也小于 {\theta _{\rm{CA}}} = 130^\circ 时的，这一现象与唐子建和杜伟[11]研究得到的结果类似，即接触角越大，表面气泡振荡过程越短。
2.1.2 接触角对气泡融合速度和铺展距离的作用规律
气泡开始融合所需时间越短，其在船底形成气层的速度越快。气泡最大铺展距离越大，意味着其能够与船底更大范围内的气泡发生融合。本文采用气泡开始融合的时间和气泡铺展距离来表征气泡融合情况。
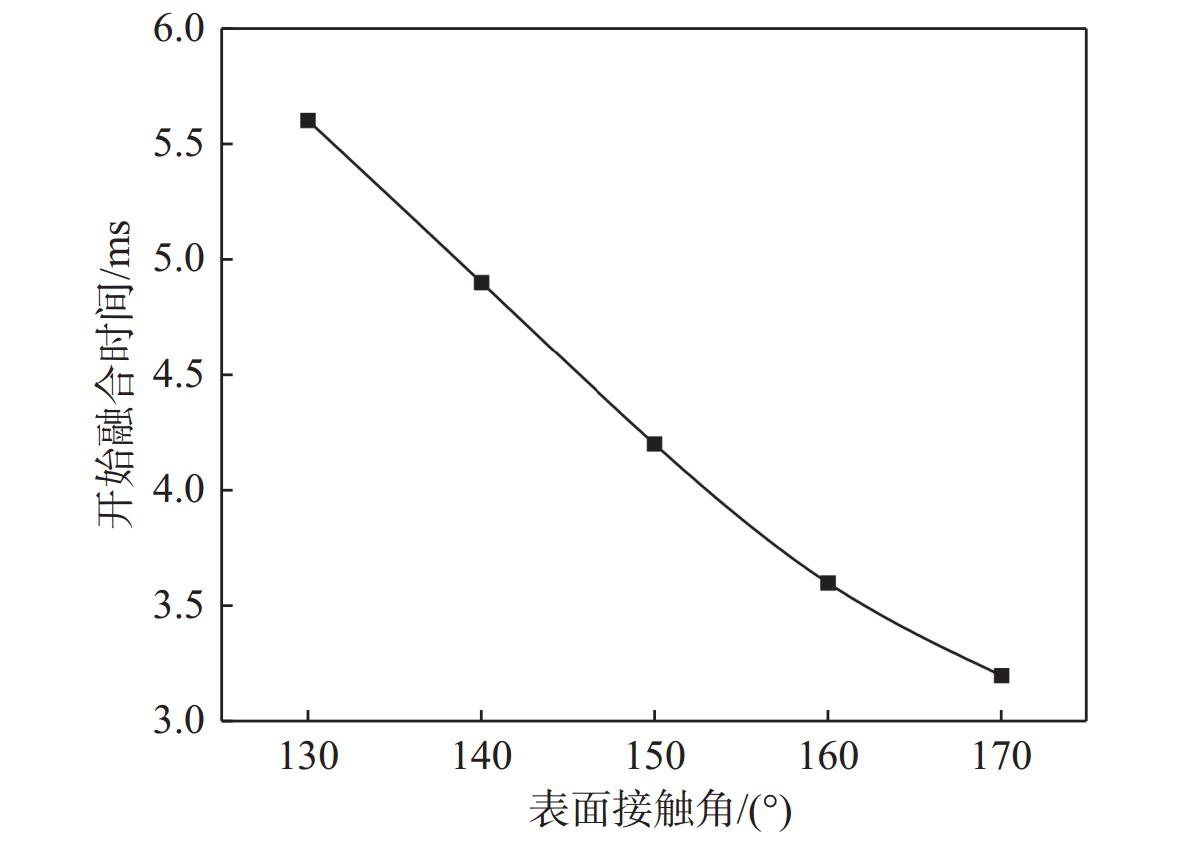
在气泡半径 r = 1 mm时，气泡开始融合的时间与壁面接触角的关系如图11所示。图中，气泡开始融合的时间为2个气泡初步接触的时间。在表面张力的作用下，2个气泡接触后开始迅速融合，随后形成一个大气泡。因此，采用本文研究中采用气泡初步接触的时间来表征气泡开始融合的时间。
![]()
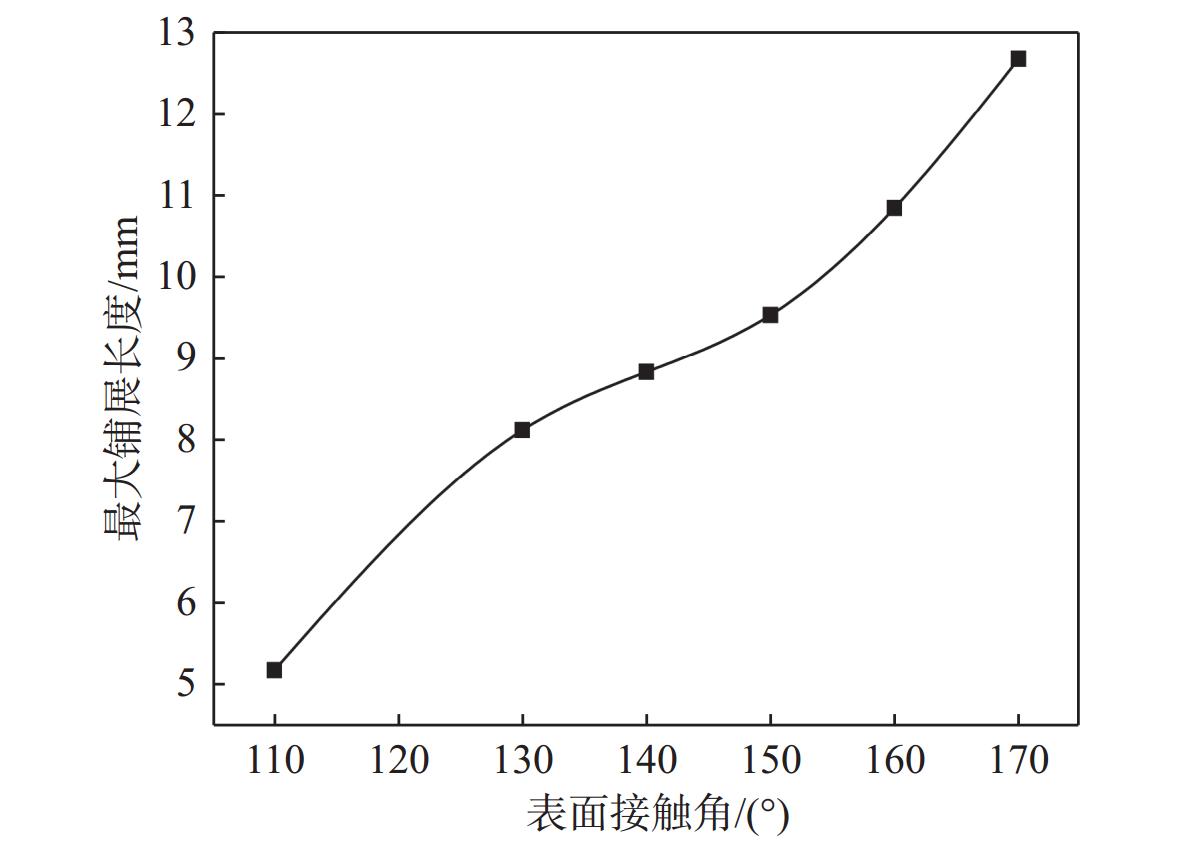
图 11 气泡开始融合时间随表面接触角的变化曲线Figure 11. Variation of bubble's initial coalescence time with surface contact angle由图11可看出，表面接触角在130°～170°时，当气泡间距 {L_{\rm{E}}} 不变时，气泡开始融合所需时间随壁面接触角 {\theta _{\rm{CA}}} 的变大逐渐减小；气泡开始发生融合的时间非常短，在6 ms内就迅速开始接触并初步融合。其中， {\theta _{\rm{CA}}} = 130^\circ 时开始融合的时间最长，为5.6 ms，而 {\theta _{\rm{CA}}} = 170^\circ 时仅3.2 ms，相比 {\theta _{\rm{CA}}} = 130^\circ 时时间减少了42.9%，显著缩短了开始融合所需的时间。接触角实质上反映的还是液体与固体表面的相互作用强度，随着接触角的增大，壁面疏水性会增强，而最为关键的是，超疏水意味着超亲气。亦即，接触角越大，亲气作用越强，壁面对气体的吸引力越大。此外，力的增大使得三相接触线的移动速度增快，导致气泡铺展的最大范围变大，这与Xiao等[5]研究得到的结论是一致的，即疏水性的增强伴随着亲气能力的增强。而随着气泡的铺展，气体和液体交界面变广，气液表面张力快速增长，直至气固表面张力与气液表面张力和液固表面张力达到平衡。
气泡最大铺展长度与表面接触角的关系如图12所示。随着接触角的增长，铺展长度显著增长，这与李国胜等[27]实验观察得到的结果一致，即表面疏水性的增强会提高气泡的最大铺展范围。两个初始半径r = 1 mm、气泡间距 {L_{\rm{E}}} = 2 mm的半圆形气泡，在超疏水表面上的铺展距离超过9.4 mm，在气泡初始铺展范围的基础上提升了138%，从而极大地改善了船底表面气泡的融合程度。以上结果表明，在气泡减阻过程中，超疏水表面的气泡能够迅速铺展并与附近更大范围的气泡迅速融合，使气层在船底分布得更均匀广泛，从而有助于减阻效果及其稳定性的提升。
![]()
图 12 气泡最大铺展长度随表面接触角的变化曲线Figure 12. Variation of bubble's maximum spreading length with surface contact angle2.2 气泡间距对气泡融合的影响
在气泡减阻过程中，船底表面的气泡间距复杂多变，其大小一定程度上决定了气泡能否发生融合以及气泡开始融合所需的时间，进而影响气泡发生融合时的不同铺展状态，并对气泡的总体融合过程产生巨大影响。因此，本节将探究气泡间距 {L_{\rm{E}}} 对融合过程的影响。
根据计算结果可知，当表面接触角 {\theta _{\rm{CA}}} = 90^\circ 时，两个气泡能够融合的临界距离为0.2D，这与吕雅琪[26]得到结论也是一致的。当表面张力系数一定时，在临界距离内气泡会在表面张力的作用下相互吸引。随着表面接触角的增大，2个气泡能够融合的最大间距迅速增大，其中 {\theta _{\rm{CA}}} = 150^\circ 时2个气泡能够融合的临界距离为2.1D。下文主要关注 {\theta _{\rm{CA}}} = 150^\circ 时气泡间距对气泡融合的影响。
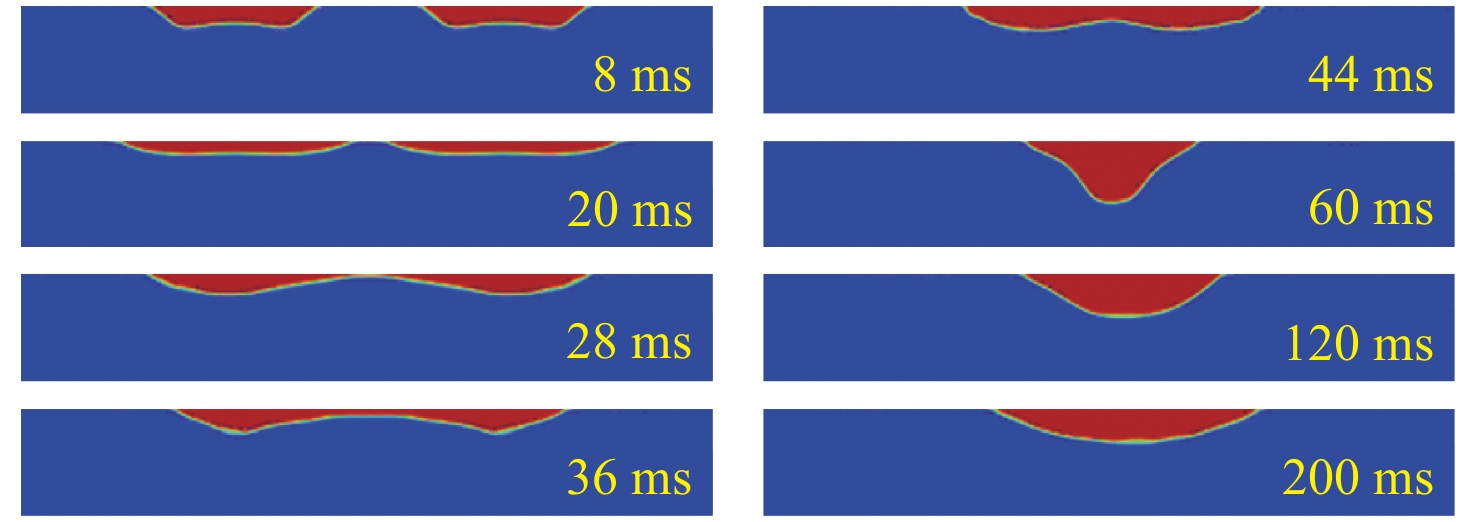
当 {L_{\rm{E}}} = 0 mm时，两个气泡靠近原点的边界是重合的，气泡在计算开始时发生了融合。如图13所示，当 {L_{\rm{E}}} = 2.1D 时，气泡在铺展到极限时，靠近彼此的两端才开始贯通，形成了薄薄的一条气液混合区域。在2个气泡开始收缩时，该区域逐渐变大，通过表面张力牵引着两侧气泡融合，形成一个较大的气泡，最后气泡开始振荡直至稳定。
![]()
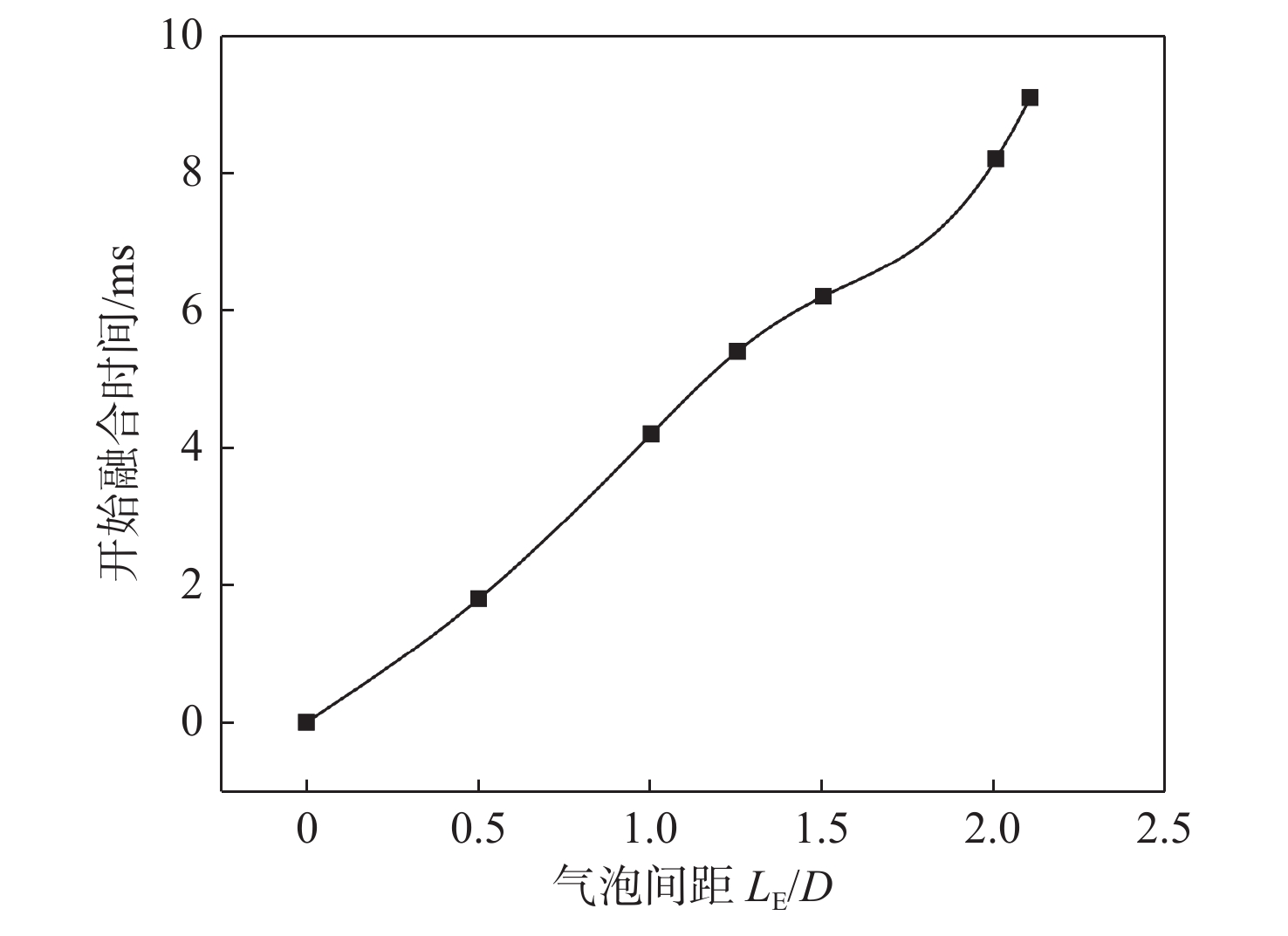
图 13 气泡间距 {L_{\rm{E}}} = 2.1D时的气泡融合过程Figure 13. Bubble coalescing process when {L_{\text{E}}} = 2.1D气泡开始融合的时间与气泡间距的关系如图14所示。在气泡能够发生融合的情况下，即气泡间距 {L_{\rm{E}}} 从0到临界距离2.1D区间，随着气泡间距的增加，气泡开始融合所需的时间逐步增加。气泡间距的增加导致三相接触线需要移动的距离增加，而表面接触角保持不变，壁面对气泡的吸引力并没有增大，三相接触线的移动速度并未增快，这必然导致气泡开始融合所需的时间增加。
![]()
图 14 气泡开始融合时间随气泡间距的变化关系曲线Figure 14. Variation of bubble's initial coalescence time with bubble spacing当 {L_{\rm{E}}} 接近气泡融合的临界距离 2.1D 时，气泡开始融合的时间增长速率变大。当 {L_{\rm{E}}} = 2.1D 时，上述时间为9.1 s，较 {L_{\rm{E}}} = 2D 时增加了0.9 s，因为此时气泡铺展接近极限，接触线移动速度缓慢。
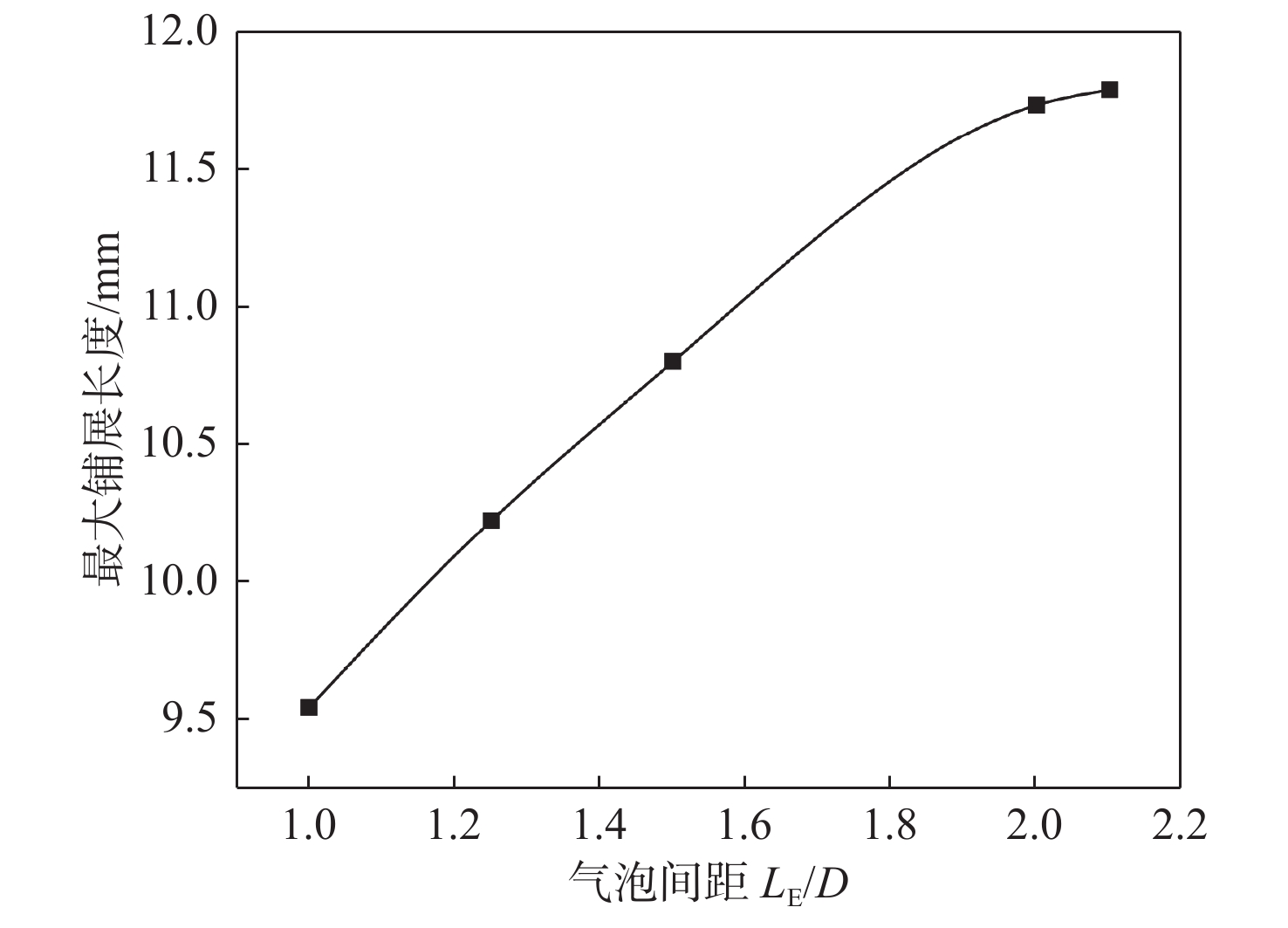
图15展示了气泡最大铺展距离与气泡间距的关系。在壁面上气泡初始覆盖范围为4 mm。当 {L_{\rm{E}}} = 0D 时，最大铺展距离为6.53 mm，这意味着其向外铺展了2.53 mm，且与附近距离2.53 mm的气泡能够再次发生融合。在气泡能够发生融合的情况下，最大铺展距离随着气泡间距的增大而增大，但变化速率略微减小。改变气泡间距，使得相同条件下气泡开始融合的时间有所不同。按照上节内容，在发生融合前气泡形态会一直发生变化，气泡间距的改变导致气泡发生融合时自身的形状和运动特性发生变化，这将极大地影响气泡融合后的运动特性。吕雅琪[26]的研究也印证了这一点，即气泡间距会影响气泡融合的速度。气泡间距较小时，气泡开始融合的时间较早，两个内侧接触线牵引着气泡向外铺展的力会在气泡接触时抵消，导致此方向的铺展停滞。此时，在表面张力的作用下，气泡产生向融合后气泡中心的牵引力，使左右气泡另一端的铺展放缓，气泡铺展长度变小。因此，气泡间距越小，气泡融合时的最大铺展距离越小。
![]()
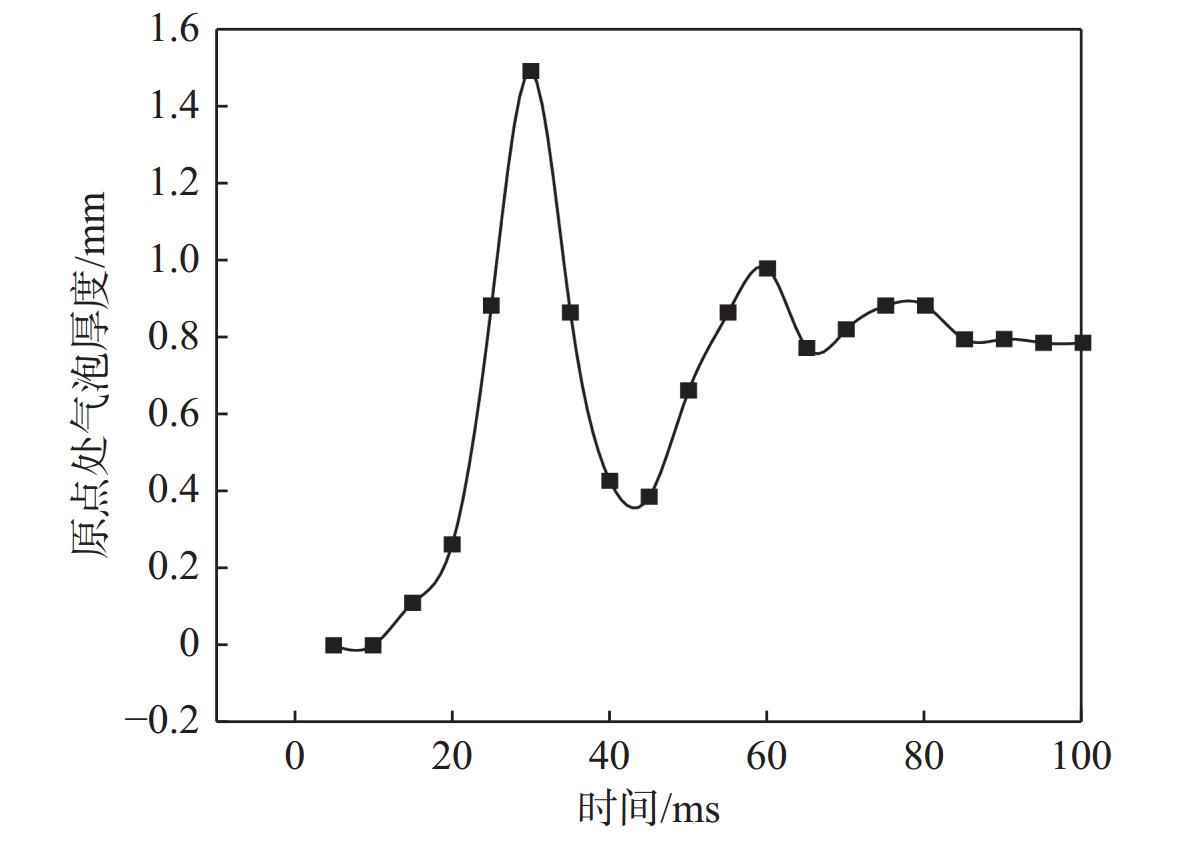
图 15 气泡最大铺展长度随气泡间距的变化曲线Figure 15. Variation of bubble's maximum spreading length with bubble spacing临界距离直接影响壁面上气泡的厚度变化。图16所示为 {L_{\rm{E}}} = 2.1D 时原点处对应的气泡厚度（气泡中心气体厚度）随时间的变化曲线。由图可见，随着时间的增加，气泡中心气体厚度逐渐增大，最高达1.5 mm，接着气体在表面张力的主要作用下开始向壁面运动，然后远离壁面，如此周期性循环。然而，此时气泡的振荡幅值逐渐减小，其动能耗散完后，将保持相对稳定的形态，厚度不再变化。与此类似，李国胜等[27]对气泡与疏水表面发生碰撞过程中接触面积的研究也表明，随着气泡发生振荡，接触面积的振荡幅值逐渐减小，当动能耗散完后，接触面积保持在一个稳定值。
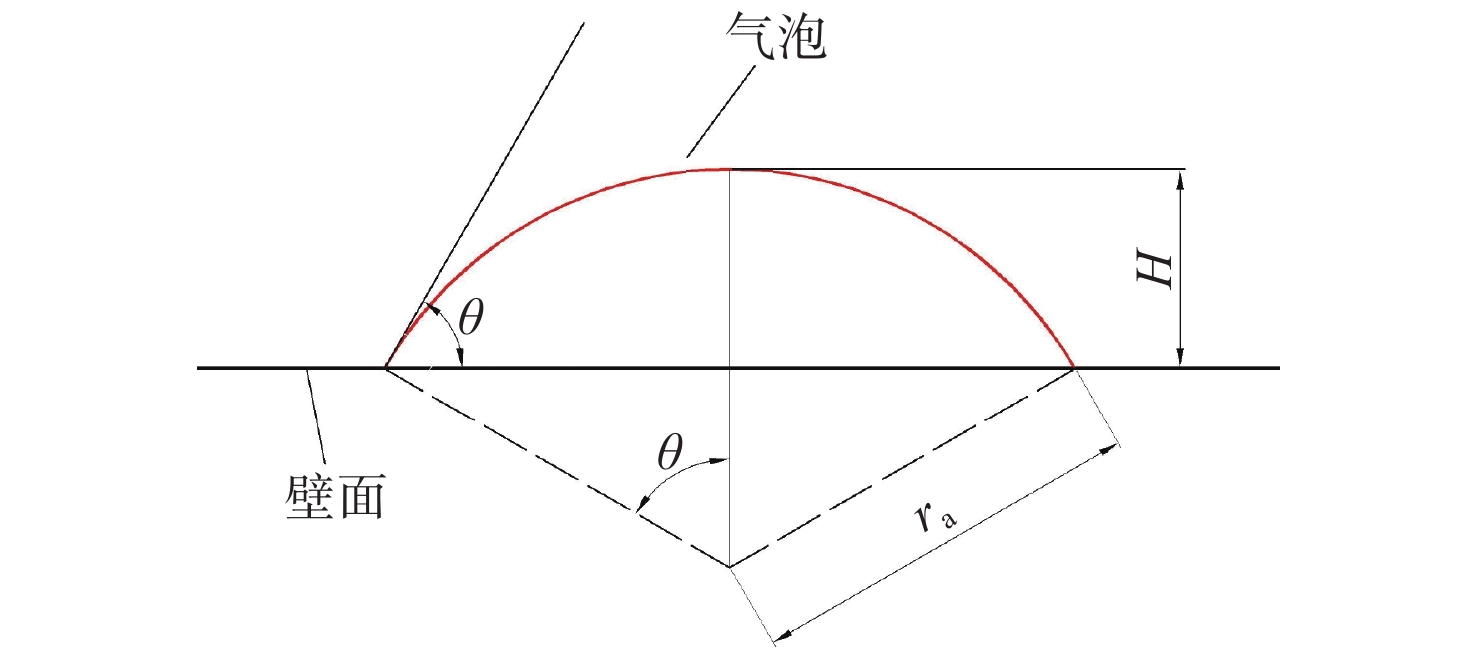
由于表面接触角 {\theta _{\rm{CA}}} 是超疏水表面的固有性质，其值是一定的。此外，考虑到质量守恒原则，在融合气泡的形状稳定后，气泡中心的气体厚度H是可通过理论求解获得的。朱智成[24]在气泡与复杂壁面作用研究中也使用了类似方法预测三维气泡中心的气体厚度。结合图17可得，融合完成后气泡半径 {r_{\rm{a}}} 与初始气泡半径r的关系如下：
\theta \text{π}r_{\rm{a}}^2/180\text{°}-r_{\rm{a}}^2\mathrm{sin}\theta\cdot\mathrm{cos}\theta={{\text{π}} }r^2 (11) 式中， \theta 为气液接触面在三相接触点处的切线与壁面的夹角， \theta = 180^\circ - {\theta _{\rm{CA}}} 。
气泡中心的气体厚度H由下式求得：
H={r}_{\text{a}}\cdot (1-\mathrm{cos}\theta ) (12) 由于表面接触角 {\theta _{\rm{CA}}} = 150^\circ ，此时 \theta = 30^\circ ，根据以上公式求得气泡中心气体厚度H = 0.79 mm。如图16所示，本文数值计算所得气体厚度约为0.786 mm，与理论值仅存在0.5%的误差。
2.3 气泡尺寸对气泡融合的影响
在气泡减阻过程中，不同尺寸的气泡发生融合的现象普遍存在。气体与水的密度差异较大，气泡尺寸会影响气泡的稳定性和运动融合特性。
首先，考虑不同尺寸气泡的融合情况。流场左右边界条件相同，保持右侧半圆形气泡半径r = R不变，改变左边气泡的半径。同时，保持表面接触角为 {\theta _{\rm{CA}}} = 150^\circ ，气泡间距 {L_{\rm{E}}} = 1.5D 。
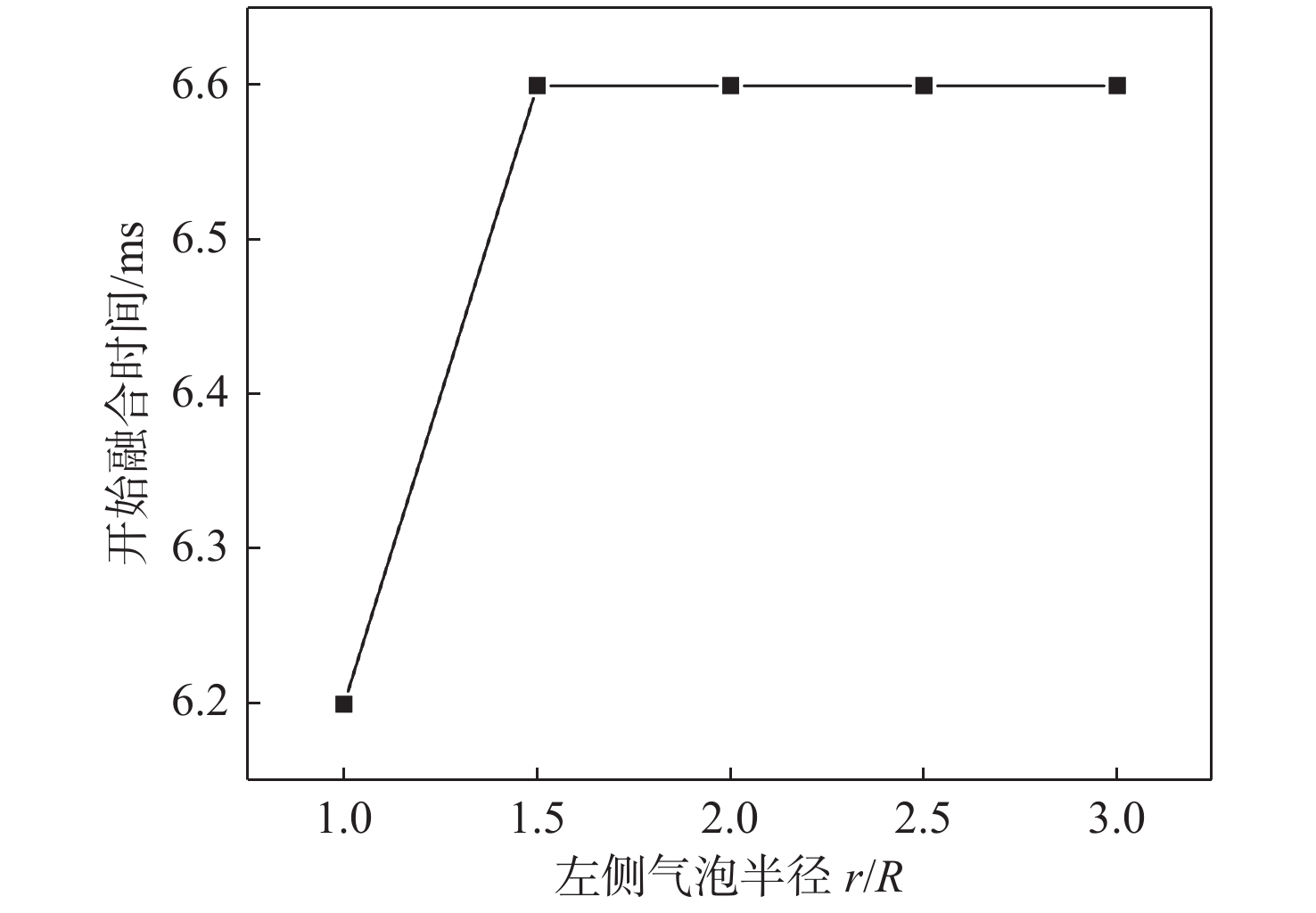
气泡开始融合时间随气泡大小变化的关系如图18所示。当左右气泡半径r均为R时，气泡开始融合的时间为6.2 ms，而左侧气泡半径在（ 1.5R , 3R ）区间内时，气泡开始融合的时间基本保持在6.6 ms左右。值得注意的是，气泡间距 {L_{\rm{E}}} 保持不变，右侧气泡半径也保持不变，这表明，在此区间内，左侧气泡的接触线在壁面上的移动速度基本相同，几乎不受气泡半径的影响。
![]()
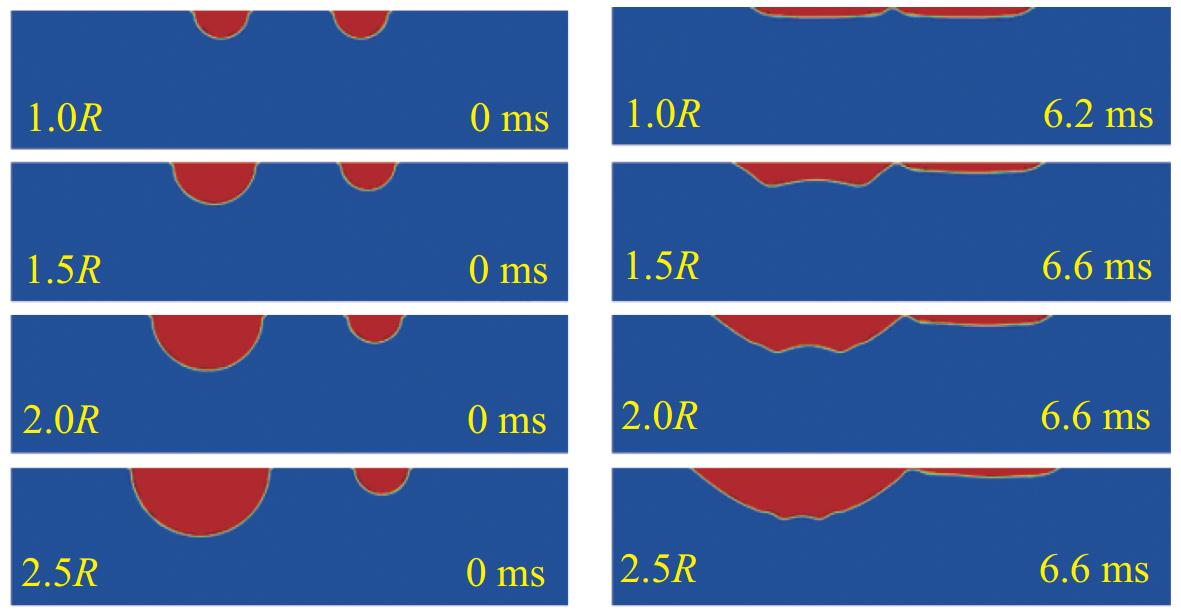
图 18 气泡开始融合时间随左侧气泡半径的变化曲线Figure 18. Variation of bubble's initial coalescence time with leftside bubble radius不同半径的气泡在开始融合时，初始形态和开始融合的形态如图19所示。当左侧气泡半径r = R时，在开始融合时刻，其已在壁面上达到较好的铺展状态，进而再开始融合。在（ 1.5R , 2.5R ）区间，左侧气泡还未完全铺展达到扁平状时，气泡已开始融合。这说明，在一定半径区间内和气泡初步铺展过程中，气泡在超疏水壁面上铺展的速度相同，不随气泡半径r变化。其原因在于，当气泡半径超过某值后，气泡都处在同一铺展阶段，此时气泡受到的表面张力相比重力非常小，这一点也可以由朱智成[24]的研究所证明，即气泡的铺展开始由重力主导。当重力加速度g恒定时，气泡三相接触线的移动速度受气泡半径的影响微乎其微，气泡开始融合的时间基本不变。
![]()
图 19 气泡初始形状（左）以及开始融合时形状（右）Figure 19. Initial shapes of the bubbles (left) and the shapes as the coalescence begins (right)当左侧气泡半径r = 2R时，气泡融合过程如图20所示。可见，不同尺寸的气泡融合时，大气泡右侧与小气泡快速聚并，气泡的主要体积先向右侧移动。此外，还可以观察到气泡垂向和横向都存在振荡，最后，融合的气泡仍将向壁面中心运动。左侧气泡半径在（ 1.5R ， 3R ）区间时，不同尺寸的气泡融合均出现相同现象。这说明，在一定条件下，超疏水表面融合生成的大气泡仍位于壁面中心位置，并未发生气泡朝某一侧聚集的现象。
![]()
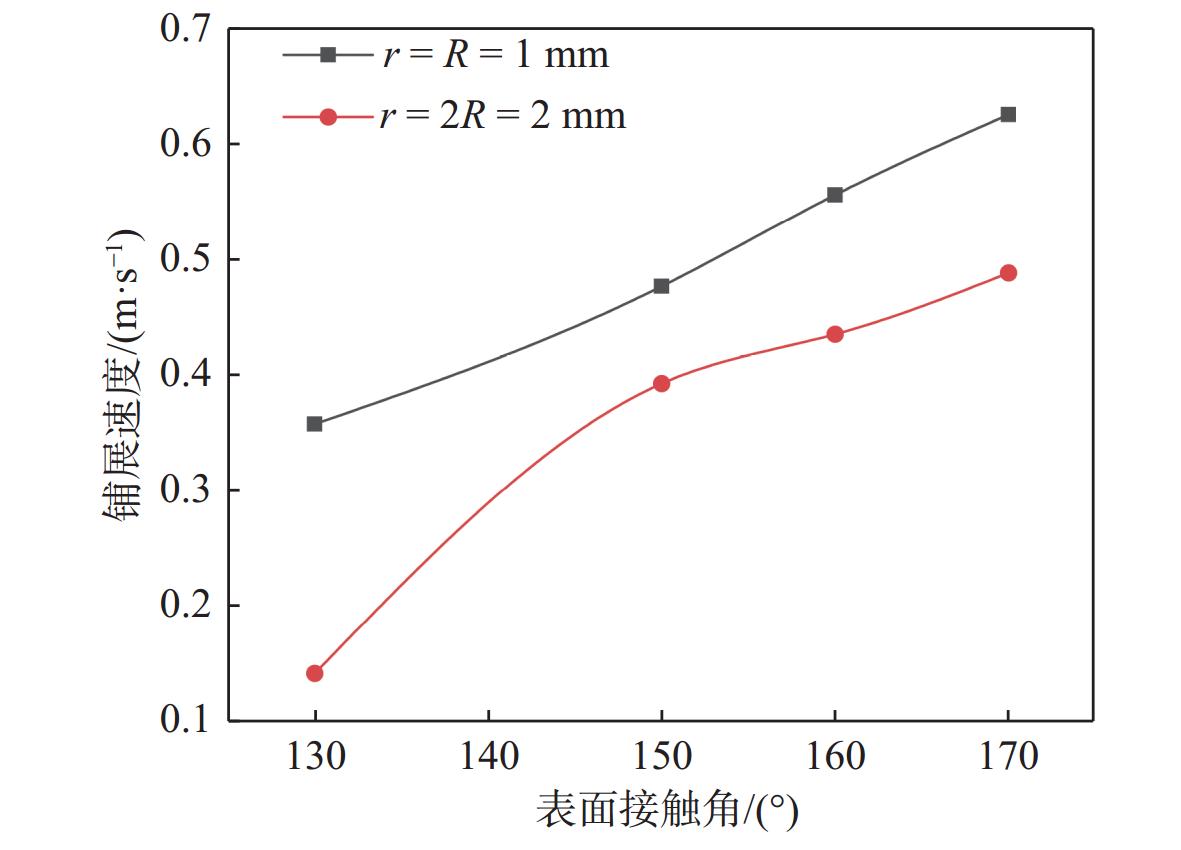
图 20 当左侧气泡半径为2R时的气泡融合过程Figure 20. Bubble coalescence process as the left bubble radius is 2R为进一步研究气泡尺寸对气泡融合和铺展的影响，本文将气泡半径增大为2R，保持气泡间距 {L_{\rm{E}}} = 4 mm不变，对两个相同尺寸气泡的融合和铺展进行模拟。在r = 2 mm和r = 1 mm时，气泡铺展速度 {v_{\text{s}}} 随表面接触角 {\theta _{\rm{CA}}} 的变化曲线如图21所示。相比两个半径r均为1 mm时，r = 2 mm的气泡铺展速度 {v_{\text{s}}} 较小。当表面接触角 {\theta _{\rm{CA}}} < 150^\circ 时，气泡铺展速度差异较大，小尺寸气泡铺展速度是大尺寸气泡的2.5倍；当壁面为超疏水表面（即 {\theta _{\rm{CA}}} \geqslant 150^\circ ）时，气泡铺展速度相差较小，小尺寸气泡最多只比大尺寸气泡快28.1%。
![]()
图 21 气泡开始融合时间随表面接触角的变化曲线Figure 21. Variation of bubble's initial coalescence time with surface contact angle从Laplace方程可知，在表面张力一定的情况下，小尺寸气泡内外压强差大于大尺寸气泡，前者水平方向的Laplace应力 {F_{\rm{LPH}}} 较大，移动接触线运动速度较快，所以铺展速度大于后者。以上结果表明，适当地减小气泡半径，能够促进气泡铺展速度的增加。对于毫米级气泡而言，超疏水表面可以显著加速气泡之间的融合过程。
3. 结 论
本文使用VOF模型，采用数值模拟方法，研究了润湿性表面气泡的融合和铺展过程，总结了表面润湿性、气泡间距、气泡尺寸对气泡融合特性的影响规律。得到的结论如下：
1） 气泡融合特性与表面润湿性高度相关。提高表面疏水性可以增强壁面对气泡的亲和作用及稳定作用，且能够加快气泡融合速度，扩展气泡融合范围。
2） 气泡间距对气泡的融合特性有着显著影响。在气泡能够发生融合的情况下，气泡间距的增加导致气泡初始融合时间延长，但使得气泡融合范围变得更广。
3） 气泡尺寸对气泡融合特性也存在显著影响。增大气泡尺寸将减缓气泡在表面的铺展速度，也不利于加快气泡融合。
综上所述，研究润湿性表面气泡融合问题，需要考虑表面润湿性、气泡间距和气泡尺寸的影响。后续研究可以针对这些参数进行选择优化，以获得更好的气泡融合效果。
-
![]()
图 4 气泡靠近和融合过程与实验结果（黑白图片所示[16]）对比
Figure 4. Comparison of bubble approach and coalescing process with experimental results indicated by grey images[16]
![]()
图 9 表面接触角为170°时的气泡融合过程
Figure 9. Coalescing process of bubbles at a contact angle of 170°
![]()
图 10 表面接触角为130°时的气泡融合过程
Figure 10. Coalescing process of bubbles at a contact angle of 130°
![]()
图 11 气泡开始融合时间随表面接触角的变化曲线
Figure 11. Variation of bubble's initial coalescence time with surface contact angle
![]()
图 12 气泡最大铺展长度随表面接触角的变化曲线
Figure 12. Variation of bubble's maximum spreading length with surface contact angle
![]()
图 13 气泡间距 {L_{\rm{E}}} = 2.1D时的气泡融合过程
Figure 13. Bubble coalescing process when {L_{\text{E}}} = 2.1D
![]()
图 14 气泡开始融合时间随气泡间距的变化关系曲线
Figure 14. Variation of bubble's initial coalescence time with bubble spacing
![]()
图 15 气泡最大铺展长度随气泡间距的变化曲线
Figure 15. Variation of bubble's maximum spreading length with bubble spacing
![]()
图 18 气泡开始融合时间随左侧气泡半径的变化曲线
Figure 18. Variation of bubble's initial coalescence time with leftside bubble radius
![]()
图 19 气泡初始形状（左）以及开始融合时形状（右）
Figure 19. Initial shapes of the bubbles (left) and the shapes as the coalescence begins (right)
![]()
图 20 当左侧气泡半径为2R时的气泡融合过程
Figure 20. Bubble coalescence process as the left bubble radius is 2R
-
[1] WU H, OU Y P, YE Q. Experimental study of air layer drag reduction on a flat plate and bottom hull of a ship with cavity[J]. Ocean Engineering, 2019, 183: 236–248. doi: 10.1016/j.oceaneng.2019.04.088
[2] 秦世杰, 季盛, 孙帅, 等. 船舶气体润滑减阻应用现状及展望[J]. 中国舰船研究, 2023, 18(6): 1–10. doi: 10.19693/j.issn.1673-3185.03101 QIN S J, JI S, SUN S, at al. Current state and prospects on applications of ship drag reduction using air lubrication[J]. Chinese Journal of Ship Research, 2023, 18(6): 1–10 (in Chinese). doi: 10.19693/j.issn.1673-3185.03101
[3] 徐天南. 国内外船舶气体减阻技术应用进展[J]. 船舶, 2021, 32(6): 69–74. XU T N. Application of air lubrication drag reduction technology at home and abroad[J]. Ship & Boat, 2021, 32(6): 69–74 (in Chinses).
[4] LOHSE D. Bubble puzzles: From fundamentals to applications[J]. Physical Review Fluids, 2018, 3(11): 110504. doi: 10.1103/PhysRevFluids.3.110504
[5] XIAO Y H, ZHENG J, HE Y M, et al. Droplet and bubble wetting behaviors: The roles of surface wettability and roughness[J]. Colloids and Surfaces A:Physicochemical and Engineering Aspects, 2022, 653: 130008. doi: 10.1016/j.colsurfa.2022.130008
[6] FUKUDA K, TOKUNAGA J, NOBUNAGA T, et al. Frictional drag reduction with air lubricant over a super-water-repellent surface[J]. Journal of Marine Science and Technology, 2000, 5: 123–130. doi: 10.1007/s007730070009
[7] LATORRE R, MILLER A, PHILIPS R. Micro-bubble resistance reduction on a model SES catamaran[J]. Ocean Engineering, 2003, 30(17): 2297–2309. doi: 10.1016/S0029-8018(03)00079-9
[8] KITAGAWA A, DENISSENKO P, MURAI Y. Effect of wall surface wettability on collective behavior of hydrogen microbubbles rising along a wall[J]. Experimental Thermal and Fluid Science, 2017, 80: 126–138. doi: 10.1016/j.expthermflusci.2016.08.010
[9] 叶煜航, 凃程旭, 包福兵, 等. 不同壁面取向下超疏水平面直轨道上的气泡滑移[J]. 力学学报, 2021, 53(4): 962–972. doi: 10.6052/0459-1879-20-405 YE Y H, TU C X, BAO F B, et al. Bubble slipping on a superhydrophobic planar straight trajectory under different surface orientations[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(4): 962–972 (in Chinese). doi: 10.6052/0459-1879-20-405
[10] KIM J, LEE J S. Surface-wettability-induced sliding bubble dynamics and its effects on convective heat transfer[J]. Applied Thermal Engineering, 2017, 113: 639–652. doi: 10.1016/j.applthermaleng.2016.11.097
[11] 唐子建, 杜伟, 杜鹏, 等. 气泡碰撞亲疏水曲壁的行为特性研究[J]. 力学学报, 2022, 54(9): 2401–2408 TANG Z J, DU W, DU P, at al. Study on the behavior of bubbles colliding with hydrophilic and hydrophobic curved walls[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(9): 2401–2408 (in Chinese).
[12] 胡海豹, 王德政, 鲍路瑶, 等. 基于润湿阶跃的水下大尺寸气膜封存方法[J]. 物理学报, 2016, 65(13): 134701. doi: 10.7498/aps.65.134701 HU H B, WANG D Z, BAO L Y, at al. Maintaining large-scale gas layer by creating wettability difference on surfaces under water[J]. Acta Physica. Sinica., 2016, 65(13): 134701 (in Chinese). doi: 10.7498/aps.65.134701
[13] 孙远志, 邬智宇, 张伟, 等. 非均匀润湿性表面的气泡动力学特性[J]. 节能技术, 2019, 37(2): 166–169, 173. doi: 10.3969/j.issn.1002-6339.2019.02.015 SUN Y Z, WU Z Y, ZHANG W, et al. Bubble dynamics of non-uniform wetting surface[J]. Energy Conservation Technology, 2019, 37(2): 166–169, 173 (in Chinese). doi: 10.3969/j.issn.1002-6339.2019.02.015
[14] BRACKBILL J U, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335–354. doi: 10.1016/0021-9991(92)90240-Y
[15] BUTT H J, LIU J, KOYNOV K, et al. Contact angle hysteresis[J]. Current Opinion in Colloid & Interface Science, 2022, 59: 101574.
[16] 李昕晨. 双气泡聚并的流体力学行为研究[D]. 北京: 北京化工大学, 2015. LI X C. Study of hydrodynamics behavior of two bubbles coalescence[D]. Beijing: Beijing University of Chemical Technology, 2015 (in Chinese).
[17] 赵超, 吕明利, 贾文广. 微织结构与微气泡复合减阻数值模拟与特性分析[J]. 船舶工程, 2022, 44(4): 69–74, 80. ZHAO C, LV M L, JIA W G. Numerical simulation and characteristic analysis of composite drag reduction of micro-woven structure and micro-bubble[J]. Ship Engineering, 2022, 44(4): 69–74, 80 (in Chinese).
[18] ZHANG Y, CHEN K, YOU Y, et al. Coalescence of two initially spherical bubbles: Dual effect of liquid viscosity[J]. International Journal of Heat and Fluid Flow, 2018, 72: 61–72. doi: 10.1016/j.ijheatfluidflow.2018.05.009
[19] KUMAR A, RAY B, BISWAS G. Dynamics of two coaxially rising gas bubbles[J]. Physics of Fluids, 2021, 33(5): 052106. doi: 10.1063/5.0048595
[20] 韩蕊. 多气泡(气泡群)非线性耦合作用及融合特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2017. HAN R. Study on the nonlinear interaction and coalescence of multiple bubbles[D]. Harbin: Harbin Engineering University, 2017 (in Chinese).
[21] DRELICH J W, BOINOVICH L, CHIBOWSKI E, et al. Contact angles history of over 200 years of open questions[J]. Surface Innovations, 2019, 8(1/2): 3–27.
[22] KIBAR A, OZBAY R, SARSHAR M A, et al. Bubble movement on inclined hydrophobic surfaces[J]. Langmuir, 2017, 33(43): 12016–12027. doi: 10.1021/acs.langmuir.7b02831
[23] 叶煜航. 超亲气壁面上气泡倾斜滑移及测量方法研究[D]. 杭州: 中国计量大学, 2021. YE Y H. Study on the bubble sliding on the inclined superaerophilic surfaces and related measurement methods[D]. Hangzhou: China Jiliang University, 2021 (in Chinese).
[24] 朱智成. 气泡与复杂壁面作用的动力学研究[D]. 合肥: 中国科学技术大学, 2022. ZHU Z C. Dynamics of bubble motion on complex surface[D]. Hefei: University of Science and Technology of China, 2022 (in Chinese).
[25] SHAW D B, DEIKE L. Surface bubble coalescence[J]. Journal of Fluid Mechanics, 2021, 915: A105. doi: 10.1017/jfm.2021.173
[26] 吕雅琪. 气泡融合及其在剪切作用下的数值研究[D]. 杭州: 中国计量学院, 2016. LV Y Q. Numerical research on bubble merging and its motion in shear flow[D]. Hangzhou: China Jiliang University. 2016 (in Chinese).
[27] 李国胜, 韩加展, 邓丽君, 等. 气泡在煤炭表面的碰撞和黏附过程[J]. 煤炭学报, 2016, 41(11): 2841–2846. LI G S, HAN J Z, DENG L J, et al. Collision and adhesion process of air bubbles on coal surface[J]. Journal of China Coal Society, 2016, 41(11): 2841–2846 (in Chinese).
下载:
计量
- 文章访问数: 185
- HTML全文浏览量: 44
- PDF下载量: 40
