Numerical study on sloshing and water exchange of free-flooding hold based on CFD
-
摘要:目的
当前各类通海型船舶的应用逐年增加。这类船舶的船舱内外相连通，在运动时会发生液舱晃荡并伴随水体交换。针对这一现象，对通海型船舶载液舱段横摇时的晃荡与进出水问题进行数值模拟研究。
方法基于CFD商用软件平台，建立一左右舷开孔通海船舶的三维舱段模型，在黏性数值水池中模拟给定横摇周期和幅值下的强迫横摇运动。通过遍历不同横摇初始角与运动周期，探究开孔处进出水质量流量与工况的关系。
结果结果表明，在强迫横摇过程中，开孔处的水流呈现周期变化。横摇幅值越大，水流流量幅值比越小，且水流流量与船体横摇速度时历曲线之间的时间差越大。
结论基于所采用的CFD方法，能够较为准确地对模拟通海型船舶的晃荡与流体交换现象，开孔处的流体交换表现出很强的规律性，可据此进一步计算通海船舶的水动力性能。
Abstract:ObjectiveThe application of various free-flooding ships is increasing year by year, and the characteristic of these ships is the presence of both tank sloshing and connectivity between internal and external seawater. In order to study this specific phenomenon, a numerical simulation is conducted.
MethodUsing a CFD commercial software platform, a 3D model of a free-flooding ship section with openings on the port and starboard sides is established. The forced rolling motions under different roll periods and amplitudes are simulated in a viscous numerical water tank. Then, the relationship between the mass flow rate at the openings and the applied working conditions is studied.
ResultsThe results show that if the rolling period is bigger, the flow amplitude ratio will also be bigger and the time difference between the mass flow and the ship’s rolling velocity will be smaller.
ConclusionThe adopted method can accurately simulate the water exchange, and this water exchange will exhibit strong regularity. Based on this, further studies can be conducted on the hydrodynamic performance of free-flooding ships.
-
Keywords:
- free-flooding hold /
- CFD /
- tank sloshing /
- mass flow /
- water exchange
-
0. 引 言
通海液舱作为一种特殊船体结构，通过舷侧自由液面及以下开孔实现舱内和舱外水体交换，常应于养殖工船、两栖船等船型。与常规液舱相比，通海液舱在左右舷侧开孔处存在水体交换，而开孔处的水流交换不仅与舱内外液面高度差相关，还显著受到船体横摇运动的影响。因此，分析船体横摇运动对开孔处水流的诱导作用对于通海型船舶水动力性能的研究具有重要的意义。
目前，对于舷侧开孔船舶水动力研究方法主要分为试验方法、快速方法和黏性流方法等。众多学者对舷侧开孔船模开展了相关试验研究，Begovic等[1-3]对破损DTMB船模进行了横摇衰减和横浪试验，分析了完整和破损船的一阶和二阶横摇阻尼，以及波高变化引起的非线性效应。Manderbacka等[4]、Ruponen等[5]对一舷侧开孔的方形驳船进行了进水横摇试验，研究了不同舱室划分下进水对横摇衰减运动的影响。张相龙等[6]对一破损舱室进行强迫横摇试验，研究了舱内外贯通时大量水浸入舱室以及舱内水体晃荡的物理现象，并与完整液舱的液面晃荡进行了对比研究。
快速方法主要基于势流理论，通过适当假定考虑进出水现象以提升计算效率。Jasionowski[7]采用自由质量法将进水视为位于重心处的沿轨迹移动的自由质量点，将破舱进水问题转化成了六自由度船体与三自由度进水质量点的多体运动问题。Santos等[8]结合浅水波方程考虑破舱内水体晃荡，以更好地描述内部流体的非线性。Mackay等[9-10]通过定义开孔两侧的压降公式，采用边界元方法计算了包含和不包含透空面的实心圆柱浮体所受的波浪载荷和运动。卜淑霞等[11-12]采用Bernoulli方程表述了船体开孔处的进出水速度，同时结合近似值考虑了波浪和船体运动对破孔处水流速度的影响，以在完整船时域运动方程中实时考虑进出水对船体参数和回复力的影响。
黏性流方法考虑了水的黏性影响，能够更准确地描述物理现象。Gu[13]基于雷诺时均Naviers Stokes（RANS）方法模拟了破损船舶在波浪中的横摇运动，重点关注了舷侧破损对静水横摇衰减以及横浪运动的影响。Xue等[14]基于RANS方法模拟了破损船舶进水时的下沉以及横倾，并分析了进水导致的阻力大小和成分变化。Zhang等[15]运用光滑粒子流体动力学（SPH）方法研究了舷侧和船底开孔的船模进水的流入过程以及船体垂荡和横摇的耦合运动。Gao等[16]针对横浪破损船舶，采用求解RANS方程描述舱室内的流体运动，船体运动则采用势流求解器，建立了破损船舶的黏−势流耦合计算方法。
尽管已有研究对通海舱型船舶的水动力特性进行了探讨，但目前的研究还局限于二维[17]。本文基于STAR-CCM+软件平台，拟对左右舷侧开有圆孔的简化船段进行强迫横摇模拟，监测典型时刻通海舱内尤其是开孔附近的流场，阐述两舷侧通海船体强迫横摇时开孔处流场变化的特点，分析不同横摇周期以及横摇角对流经开孔水体流量的的影响。以期为进一步开发此类船舶运动与耐波性预报方法奠定基础。
1. 计算方法理论
1.1 流动控制方程
带自由面的流场模拟常采用多相流计算流体动力学方法，流体运动的控制方程采用如下形式的三维非定常、不可压缩RANS方程：
∂ˉui∂xi=0 (1) ∂¯ui∂t+¯uj∂¯ui∂xj=fi−1ρ∂¯p∂xi+1ρ∂∂xj(μ∂¯ui∂xj−ρ¯u′iu′j) (2) 式中：ui和uj为流体微团在i和j方向上的瞬时速度分量；fi为质量力；ρ为流体密度，其定义为ρ=2∑q=1aqρq，其中aq表示单元体积内第q相流体体积所占的体积分数，故有2∑q=1aq=1；p为压力；μ为流体动力黏性系数；u′i和u′j为脉动速度分量。采用VOF方法追踪自由面：
∂aq∂t+∂(aq¯ui)∂xi=0 (3) 本文采用STAR-CCM+软件，基于有限体积法离散求解上述控制方程。为求解雷诺应力ρ¯u′iu′j，依据Boussinesq假定，雷诺应力ρ¯u′iu′j是平均速度梯度的线性函数：
τR=−ρ¯u′iu′j=μt(∂¯ui∂xj+∂¯uj∂xi)−23ρkδij (4) 其中，μt为湍流黏度。由于控制方程中引入了μt和湍动能k，因此需要湍流模型来封闭控制方程。Begovic等[2]的研究证明，在对舷侧开孔船体横摇运动的CFD模拟中，k−ε湍流模型的计算结果与实验数据的差异在1%以内，所以本文采用SST k−ω湍流模型。计算时采用二阶分离流隐式非稳态求解器，调用SIMPLE算法对速度和压力场进行耦合迭代求解。
1.2 不确定度分析
按照ITTC验证与确认分析章程[18]进行计算流体力学（CFD）的不确定度分析。其过程可以分为验证和确认两部分。
评估数值不确定度的过程称为验证，即估计数值误差的大小、符号及其不确定度。当前通常使用参数系列加细的多重解来评估数值误差和不确定度。
定义收敛因子Rk：
Rk=εk21εk32 (5) 式中：εk21为中细解之差；εk32为粗中解之差。
可能出现的收敛状况有3种：
1） 单调收敛：0<Rk<1；
2） 波动收敛：Rk<0；
3） 发散：Rk>1。
对于单调收敛的情况，可采用广义Richardson外推法。根据三重解得到误差和准确度阶数的首项估计值：
δ∗(1)REk1=εk21rPkk−1 (6) Pk=ln(εk32/εk21)lnrk (7) 式中：rk为参数加细比；δ∗(1)REk1为首项误差；Pk 为准确度阶数。对误差的修正因子为
Ck=rPkk−1rPkestk−1 (8) 其中，Pkest是当网格无限小，渐近线范围Ck→1时首项准确度极限阶数的估计值，通常取为2[19]。
进而可以得到带修正因子的误差：
δ∗k1=Ckδ∗REk1=Ck(εk21rpkk−1) (9) 不确定度的表达式可由误差估计式得到。1）当数值解不在渐进范围即Ck远大于或小于1时：
Uk = (|Ck| + |1−Ck|)|δ∗(1)REk1| (10) 2）当数值解在渐进范围内，即Ck→1时：
Uk=|1−Ck||δ∗(1)REk1| (11) 上述验证步骤可以得到网格尺寸引起的不确定度UG和时间步长引起的不确定度UT，数值模拟的不确定度USN 可表示为
U2SN=U2G+U2T (12) 确认过程是利用基准试验数据评估数值模拟的模型不确定度USM的过程，当条件允许时，可估计建模误差δSM。比较误差E定义为试验数据D和模拟结果S之差：
E=S−D (13) 确认不确定度UV定义为
U2V=U2D+U2SN (14) 其中，UD为试验不确定度。将比较误差E、确认不确定度UV和所设定的需求不确定度Ureqd进行比较，根据其大小关系来判断是否完成确认。
2. 强迫横摇舱室进水过程数值模拟与验证
2.1 几何模型与数值模型
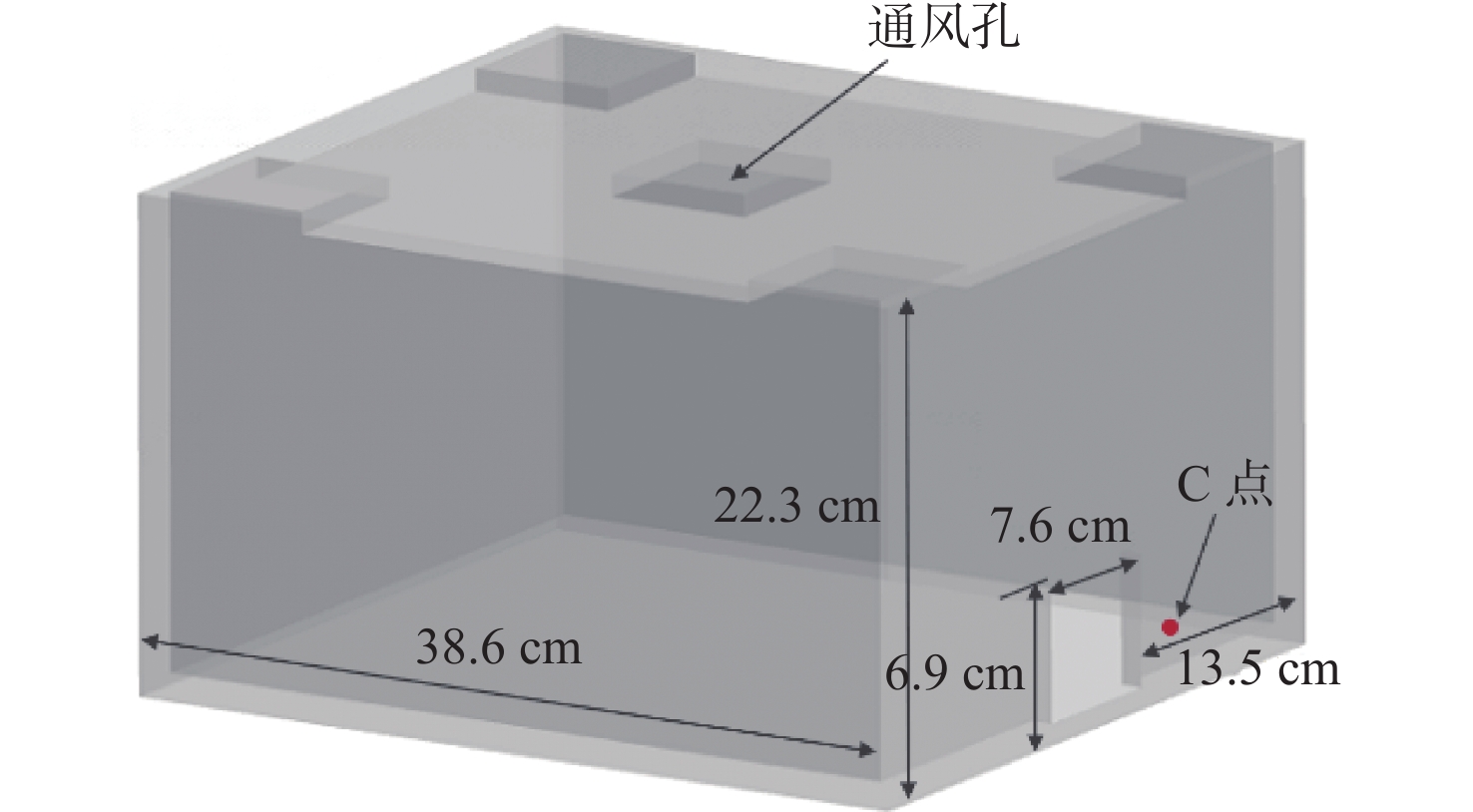
首先，通过舷侧水面以下开孔的液舱强迫横摇试验验证模型的适用性。计算模型为吴家俊等[20]在数值和试验研究中采用的侧面方形开孔单舱室，如图1所示，其外形为方形，平行于横摇轴的舷侧开有一矩形破孔连通舱内外水体，顶部开有5个开孔以排除空气压缩性的影响。模型主要参数如表1所示，其运动形式为绕中纵剖面轴线的正弦形式强迫横摇。本文监测液舱内C点的自由面高度变化进行，C点位于舷侧矩形破口右侧通风孔中心在底面的投影点（图1红点）。
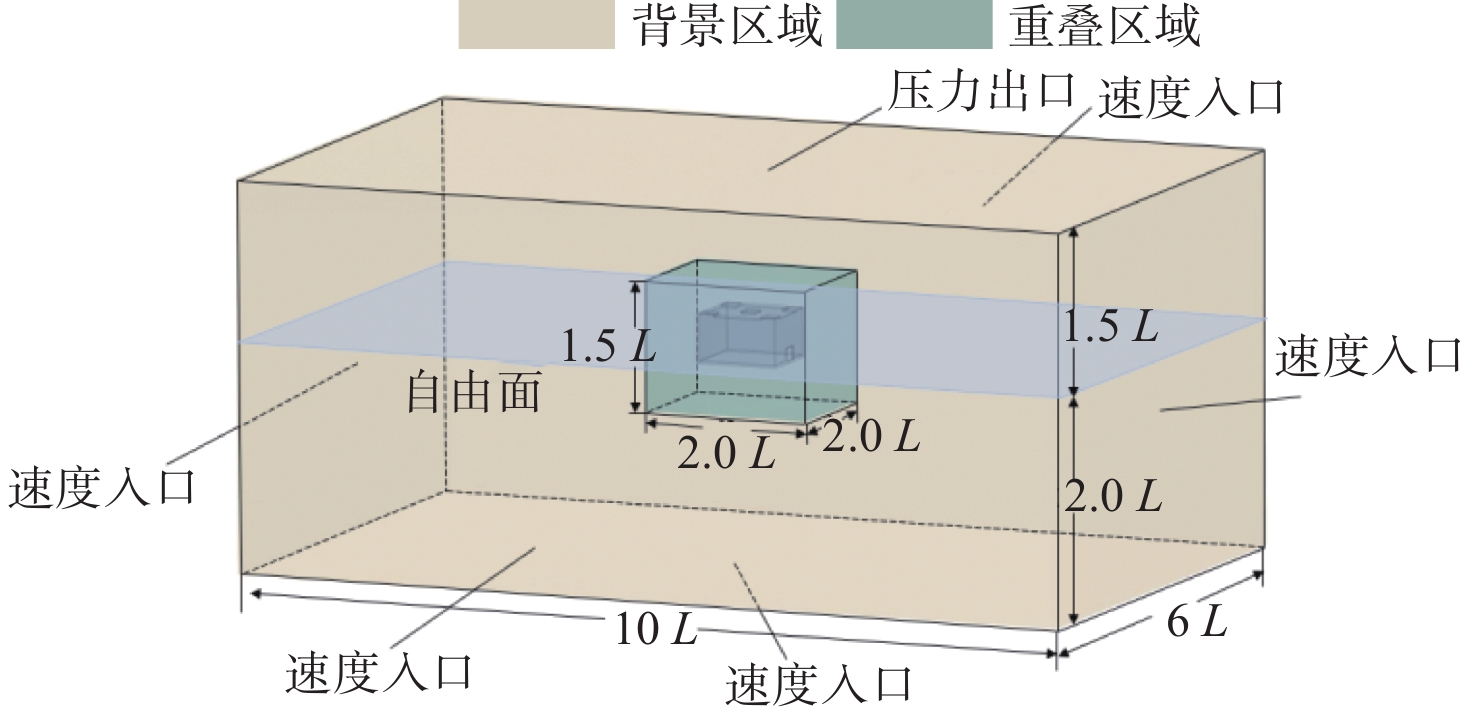
表 1 破损舱室模型主要参数Table 1. Main parameters of the damaged compartment model参数 数值 舱长L/m 0.386 舱宽B/m 0.345 舱高H/m 0.223 矩形破口尺寸/m 0.074×0.059 通风口尺寸/m 0.072×0.068 吃水d/m 0.095 利用STAR-CCM+软件建立流体域，基于重叠网格方法将计算域划分为背景区域和重叠区域，计算域的基本划分与尺寸如图2所示，重叠区域定义为：−L<x<L， −L<y<L， −L<z<0.5L。背景区域定义为：−3L<x<3L，5L<y<5L，−2L<z<1.5L。计算域的顶部为压力出口，四周和底部为速度入口，并在x和y方向设置消波区。
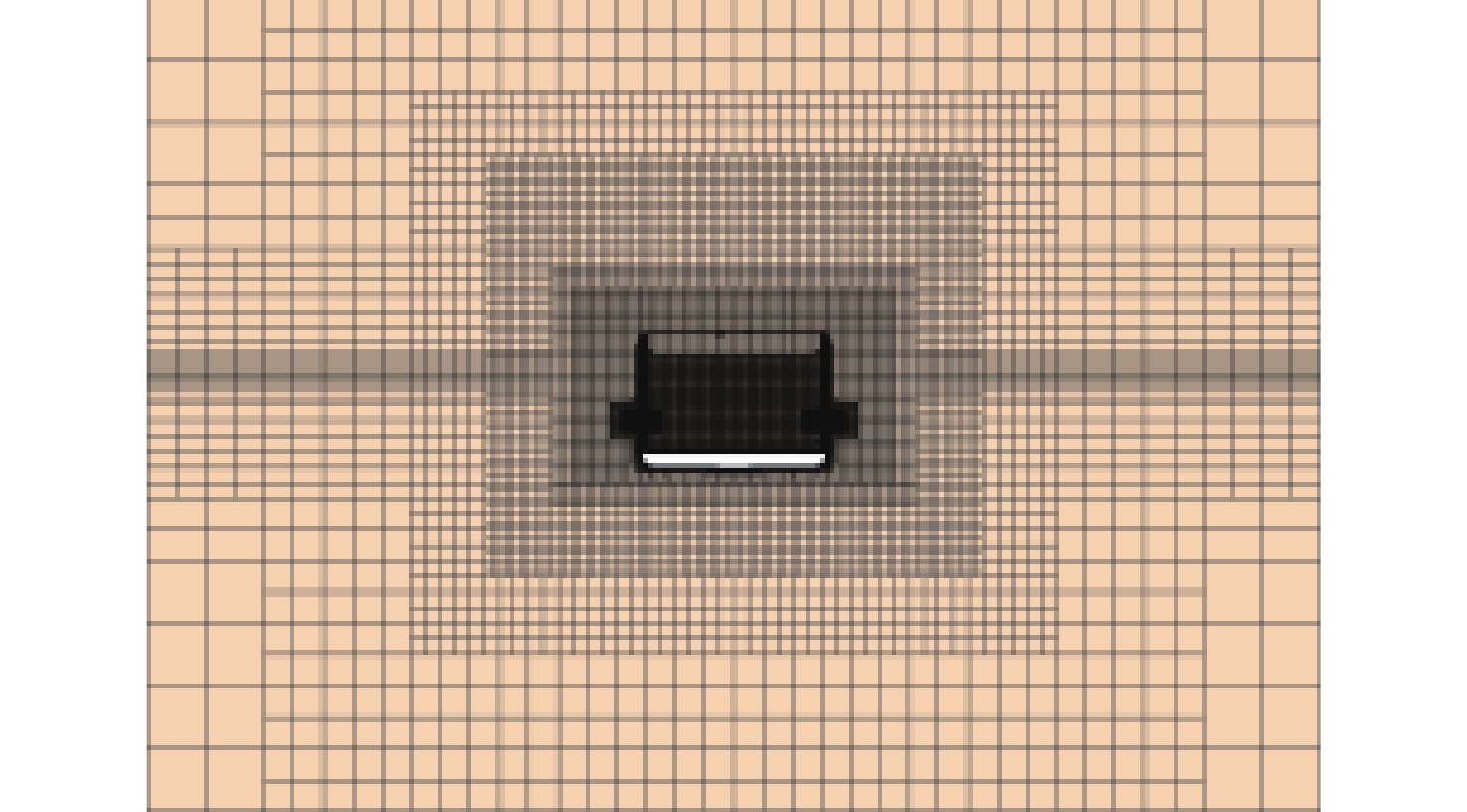
划分流体域后，采用切割体和棱柱层对区域进行网格划分，网格基本尺寸为0.015 m，为捕捉复杂流动，对整个自由面进行基本尺寸1/2的网格加密，舱口附近以及舱室内部则进行基本尺寸1/4的局部加密，以获得更精确的数值结果。为保证重叠网格交接面处插值精度，重叠区域和背景区域交接处的网格尺寸需要基本一致。图3(a)为网格横剖面图，图3(b)为开孔处局部网格放大图。在初始条件设置时，自由面位于z = 0 m处，且初始时刻舱内无水。
2.2 不确定度分析
本文对破损舱室强迫横摇进水过程进行CFD数值模拟。为定量地评估所采用数值模拟方法的准确度，运用ITTC推荐的不确定度分析方法估算误差。ITTC推荐的CFD数值模拟的不确定度分析包括验证和确认两部分[17]。其中验证是计算数值模拟的数值误差和不确定度的过程，主要考虑的数值误差来源为网格尺寸和时间步长；确认则是利用基准试验数据评估数值模拟的模型不确定度。
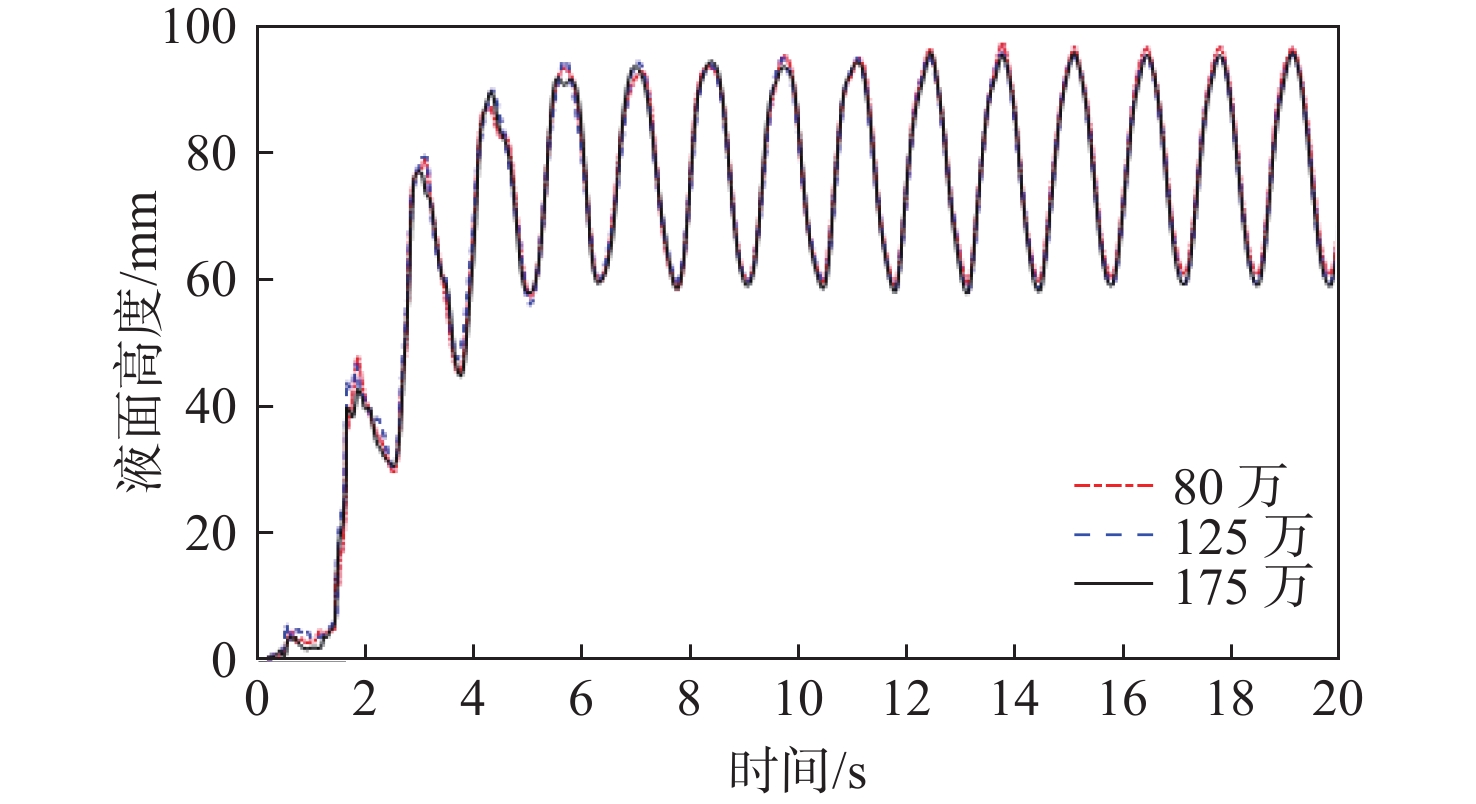
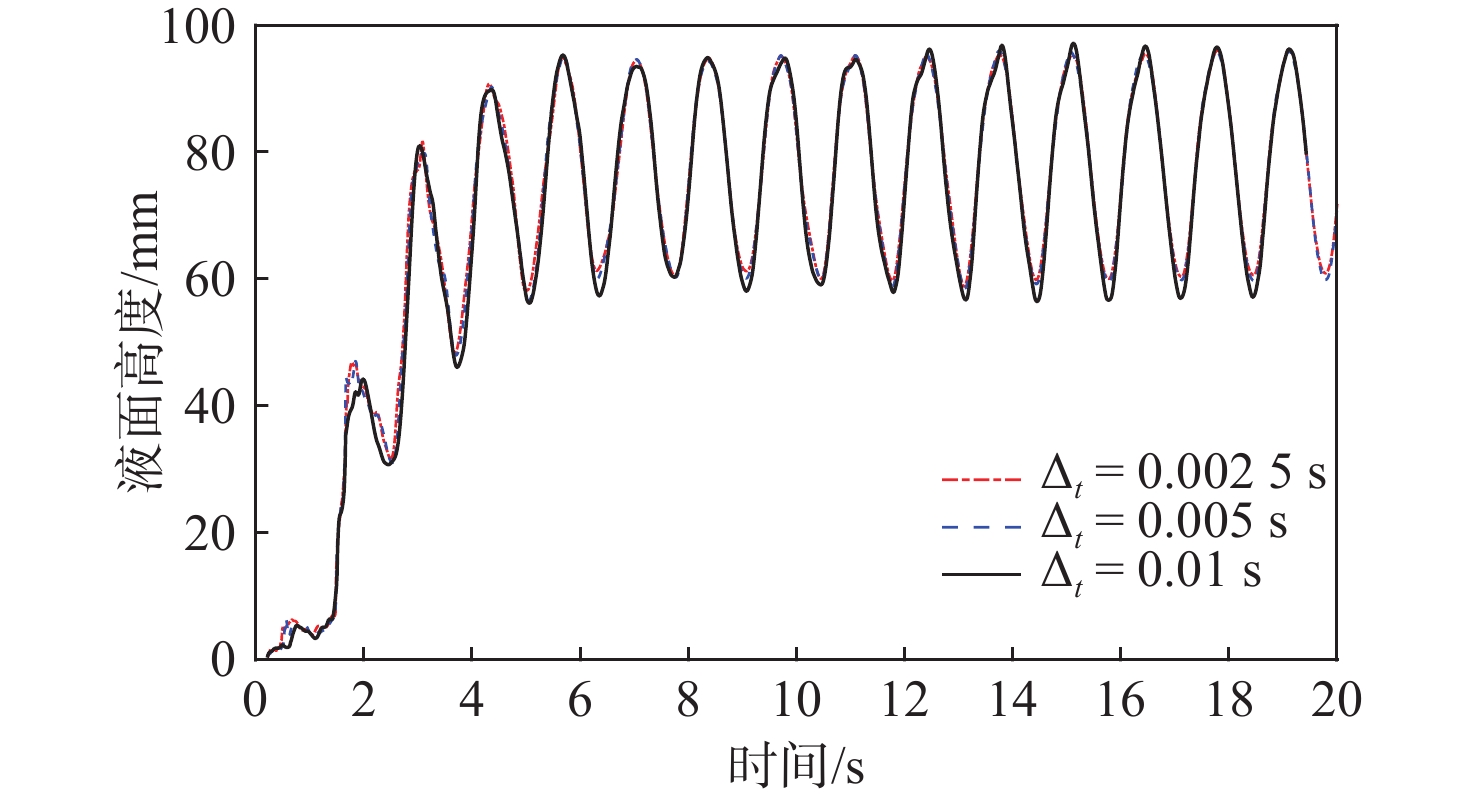
针对最大横摇角为5°，横摇周期为1.35 s的工况，以固定的加细比选取网格数为80万（粗），125万（中），175万（细），时间步长为0.002 5，0.005和0.010 s等模型参数进行计算。图4为粗、中、细3套网格下C点处的液面高度时历曲线，图5为中网格在各时间步下C点处的液面高度时历曲线。
![]()
图 4 各网格数下C点处的水位时历曲线Figure 4. Time history curve of water level at point C under each mesh number![]()
图 5 各时间步下C点处的水位时历曲线Figure 5. Time history curve of water level at point C at each time step首先进行网格不确定度分析，选取的时间步长为0.005 s。由于舱室进水时液面变化具有较强的非线性和随机性，本文取相邻时间步和网格液面高度较为稳定的周期变化阶段（10～20 s）后，各时刻相邻网格水位高度之差的平均L2范数。
L2范数的表达式为：
‖ (15) {\left\| {{\varepsilon _{{\text{G32}}}}} \right\|_{\text{2}}} = \left[\frac{1}{N}\sum\limits_{i = 1}^N {{{({\eta _{{\text{G}}3i}} - {\eta _{{\text{G}}2i}})}^2}} \right]^{{\text{1/2}}} = {\text{0}}{\text{.001 16}} (16) 式中：{\eta _{{\text{G}}1i}}，{\eta _{{\text{G}}2i}}和{\eta _{{\text{G}}3i}}分别为细、中、粗网格下液面高度时历数据第i个值; {\varepsilon _{G{\text{21}}}}和 {\varepsilon _{{\text{G32}}}} 均为两时历曲线各时间步之差。由此可以得到网格收敛因子{R_{\text{G}}}：
{R_{\text{G}}} = {\left\| {{\varepsilon _{{\text{G21}}}}} \right\|_{\text{2}}}/{\left\| {{\varepsilon _{{\text{G32}}}}} \right\|_{\text{2}}}{\text{ = 0}}{\text{.568}} (17) 由于 0 < {R_{\text{G}}} < 1 ，网格收敛条件为单调收敛。采用广义Richardson外推法进行不确定度分析。
采用同样方法对时间步长进行收敛性分析，计算得到：
{\left\| {{\varepsilon _{{\text{T21}}}}} \right\|_{\text{2}}}{\text{ = 0}}{\text{.000 495, }}{\left\| {{\varepsilon _{{\text{T3}}2}}} \right\|_{\text{2}}}{\text{ = 0}}{\text{.001 37, }}{R_{\text{T}}}{\text{ = 0}}{\text{.361}} (18) 按照ITTC推荐方法进行验证，结果如表2所示，表中 \bar H 为液面高度稳定之后的平均液面高度。由表可见，网格不确定度要大于时间步不确定度，数值模拟结果对于网格尺寸的依赖性强于时间步长。因此，在模拟时应该优先满足网格精度要求。
表 2 C点水位时历数值模拟验证结果Table 2. Verification results of numerical simulation of water level time history at point C参数 数值 \delta _G^ * /mm 0.661 {U_G} / \bar H /% 1.60 \delta _T^ * /mm 0.165 {U_T} / \bar H /% 0.638 \delta _{SN}^ * /mm 0.826 {U_{SN}} / \bar H /% 1.72 接下来根据ITTC建议对数值模拟结果进行确认。C点处液面高度的确认不确定度 {U_V} 为
{U_V} = \sqrt {U_{SN}^{\text{2}} + U_D^{\text{2}}} = 5.29\% \bar H (19) 液面高度时历模拟结果与试验测量结果之间误差的平均L2范数为
E = {\left\| {{\eta _{\exp }} - {\eta _{{\text{num}}}}} \right\|_{\text{2}}} = \left[\frac{1}{N}\sum\limits_{i = 1}^N {{{({\eta _{\exp i}} - {\eta _{{\text{num}}i}})}^2}} \right]^{{\text{1/2}}}{\text{ = 4}}{\text{.67\% }}\overline H (20) 液舱在强迫横摇过程中，C点处液面高度变化的数值模拟确认结果如表3所示，可见液面高度时历曲线的比较误差E小于对应的确认不确定度 {U_{\text{V}}} 。所以数值模拟的液面高度时历在 5.29\% \bar H 的程度上得到确认。因此本文所采用的中等网格与时间步长能够较为准确地模拟通海液舱强迫横摇与进水过程，后续模型也将使用相同的参数设置。
表 3 C点水位时历数值模拟确认结果Table 3. Validation results of numerical simulation参数 数值 {U_G}/\bar H /% 1.60 {U_T}/\bar H /% 0.638 {U_{SN}}/\bar H /% 1.72 {U_V}/\bar H /% 5.29 E/\bar H /% 4.67 2.3 数值与试验结果对比
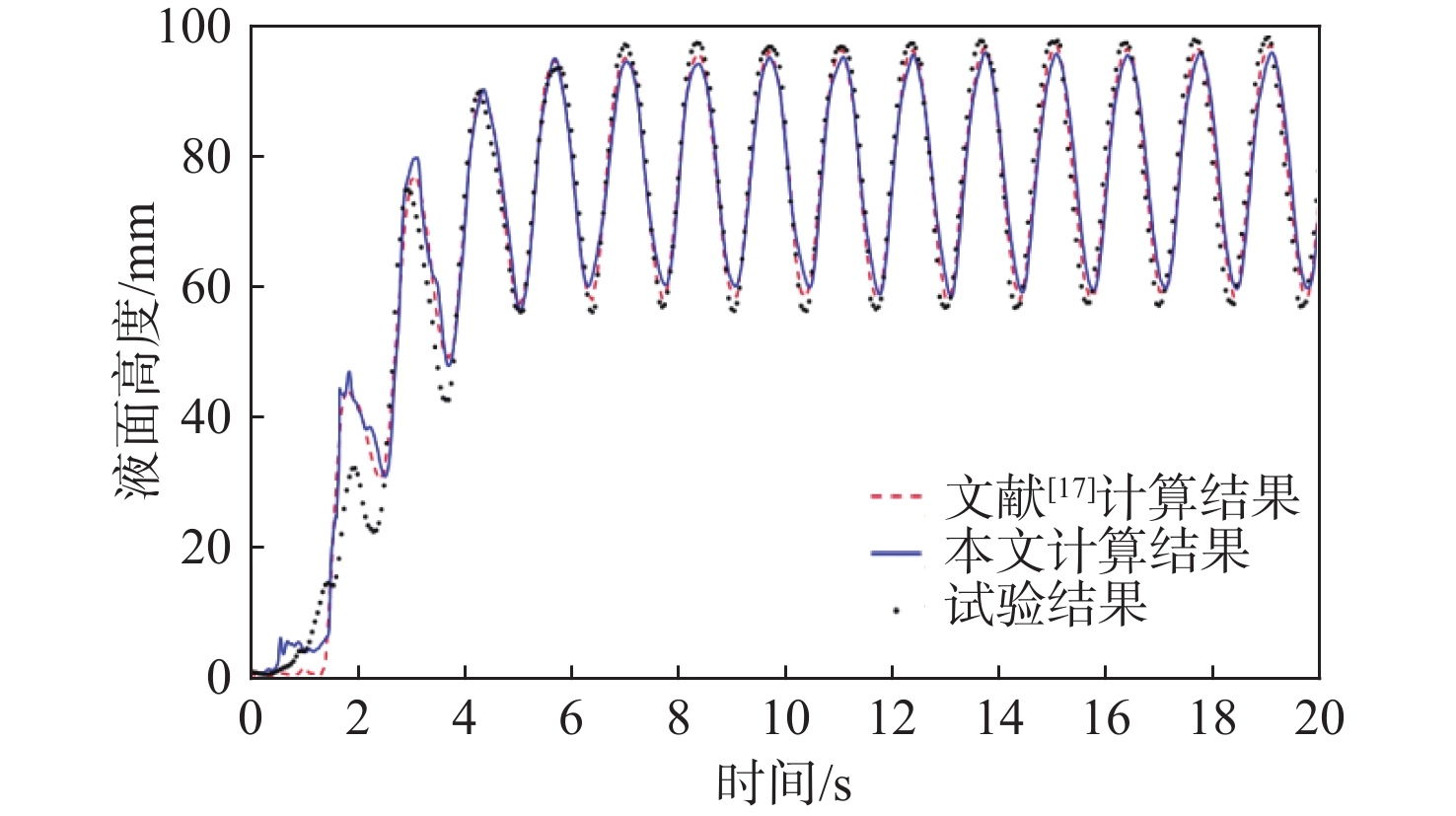
将计算得到的C点水位时历曲线与文献[17]中的C点水位时历实验数据及CFD计算结果进行对比，如图6所示。可见本文的计算结果与文献中的计算结果总体上较为接近，能够模拟出C点在进水0～1.5s内水位缓慢升高；随后液面高度迅速增大，这是因为进入舱室的水体到达另一舷侧后产生的回流到达C点。在进水初期，液面存在强非线性，液面翻卷以及飞溅会导致进水曲线不光顺，数值计算结果与实验结果之间会存在一定差异。2～8 s内水位在周期性变化中缓慢上升，随后液面保持稳定的近似简谐变化规律进行周期性晃荡。
![]()
图 6 C点处水位数值计算结果与试验结果的比较Figure 6. Comparison between the numerical results and experimental results of water level at point C截取横摇舱室中横剖面的液面形状，得到舱室进水时的典型瞬态流场如图7所示。由图可见，起初舱室内没有液体，外部流体在重力静压作用下迅速涌入舱室，并沿舱室底部向另一侧快速传播。随后液体会与侧壁发生砰击，沿侧壁爬升并形成回流向开孔方向反向传播，同时产生液面翻卷。在此过程中，进水导致舱内液面持续升高，同时也会随着船体的强迫横摇发生晃荡。最终，当内外液面高度相近时逐渐稳定，开孔处的进出水到达平衡。本文所模拟出的物理现象与文献[17]对强迫横摇舱内进水与晃荡的物理描述基本一致。
![]()
图 7 破损舱室强迫横摇中横剖面液面演化图Figure 7. The evolution of liquid level in the damaged compartment on transverse section during forced rolling motion3. 通海舱室船段强迫横摇模拟与分析
3.1 几何模型与数值模型
图8为本文计算所采用的两舷侧开圆孔的通海强迫横摇船段几何模型，该模型由一具有双底单壳结构的通海养殖工船1∶50模型的中横剖面拉伸而成。其主尺度如表4所示。与常规液货船相比，该模型的特点是在水线以下的左右两舷开有圆孔，舱内水与舷外水相互贯通，存在耦合效应。在横摇运动时，舷侧开孔处会有水流进出液舱，从而对液舱内水体的晃荡造成影响。同时，舷侧开孔处的流速大小和流动方向会实时变化，且受黏性和旋涡的影响很明显，因此本节重点研究开孔附近水体流动与横摇运动的关系。
表 4 通海舱段模型参数Table 4. Model parameters of the ship section参数 数值 舱长L /m 0.4 舱宽B /m 0.376 舱高H /m 0.230 型深D /m 0.257 圆孔半径r /m 0.015 吃水d /m 0.180 此外，养殖工船鱼舱与大气连通，模型在上甲板上开有圆孔，以使舱内气压与大气压保持一致。计算域的设置方法与第2节一致，网格划分上也基本一致（图9），仅在两舷侧开孔附近进行局部网格加密，网格总数约为155万。
3.2 通海舱开孔处流场分析
由前述计算可知，在强迫横摇过程中，通海液舱内外液面高度差很小，因此开孔处的水体流量并非由静水压力所驱动，而是主要由船体运动的诱导以及水体自身的惯性所致。为分析船体横摇对开孔处水流的影响，本节选取了不同横摇周期（0.50，1.00，1.25，1.50，2.00和3.00 s）以及不同横摇幅值（2.5°，5.0°和7.5°）的工况，对船段进行了强迫横摇CFD计算。由于舱内平底的影响，开孔处的水流在舱内相对于船体呈近似水平流动，因此在开孔处重点监测了进出水体的质量流量，以反映开孔处水体的平均变化情况。
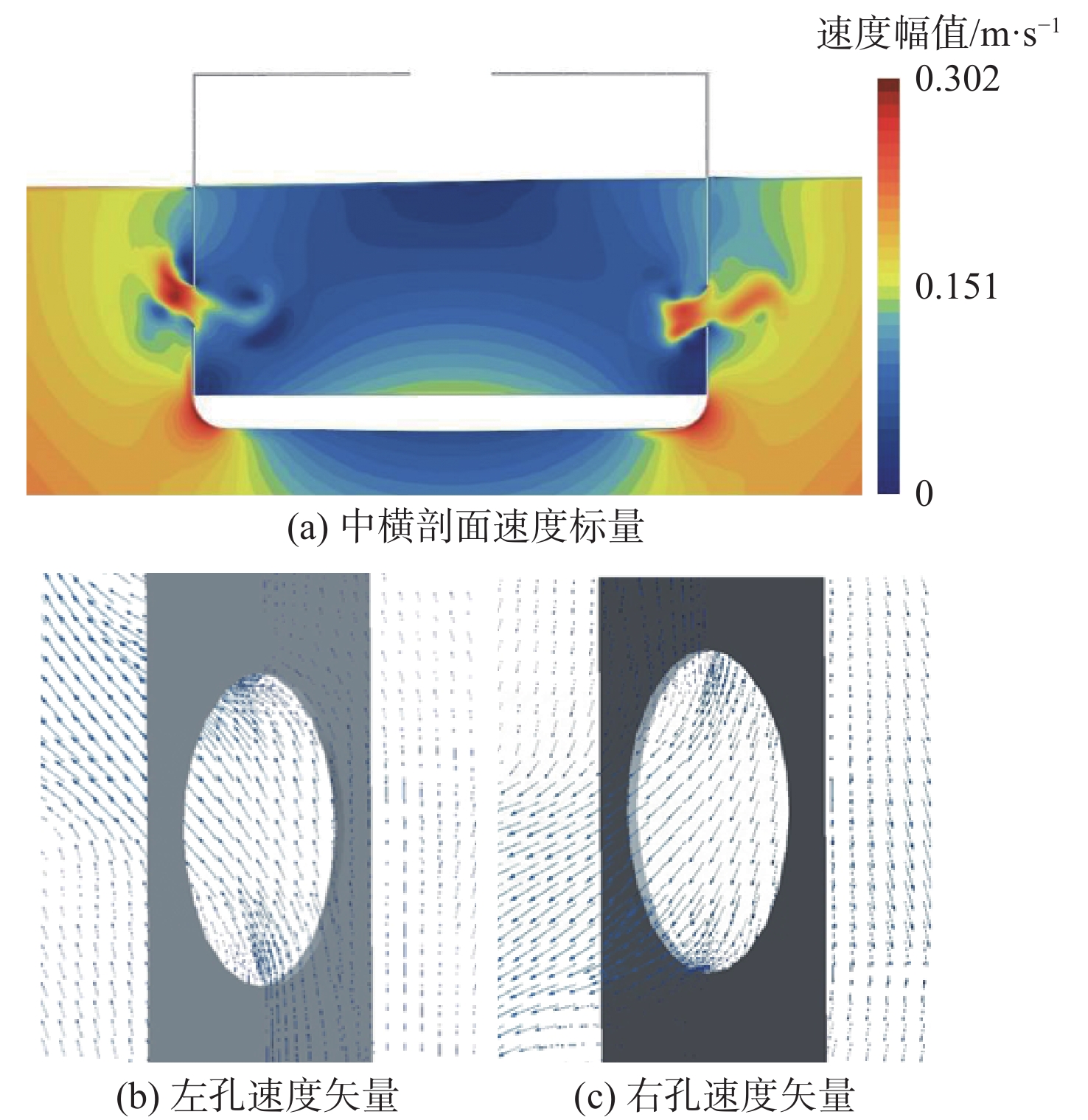
图10～图13为横摇周期为1 s、横摇幅值为5^\circ 工况下通海液舱中横剖面以及开孔附近典型时刻的流场图。由于本文重点关注开孔处水流对通海液舱内流场的影响，因此所监测的速度均为固定于船体的动坐标系下的相对速度。
图10为t=0.5 s时的流场状态。由于图10(a)显示的是相对速度的模，因此受船体自身角速度的影响，靠近船体区域的速度相小于远离船体区域的速度。t=0.5 s时，船体的横摇角为0，但是顺时针横摇的角速度达到最大值，在船体运动的诱导下，左侧开孔有水体流入，而右侧开孔有水体流出，以维持舱内水体总量基本不变，且内外液面基本保持平整。由图10(b)和图10(c)可以看出，此时开孔处流线较为光顺，液舱内外水体速度方向在动坐标系下相同。图11为t=1 s时的流场状态，经过半个周期后，船体的横摇角再次变为0，但此时船体逆时针横摇的角速度达到最大值，流场状态与图10基本相同，只是水流速度方向与t=0.5 s时相反。
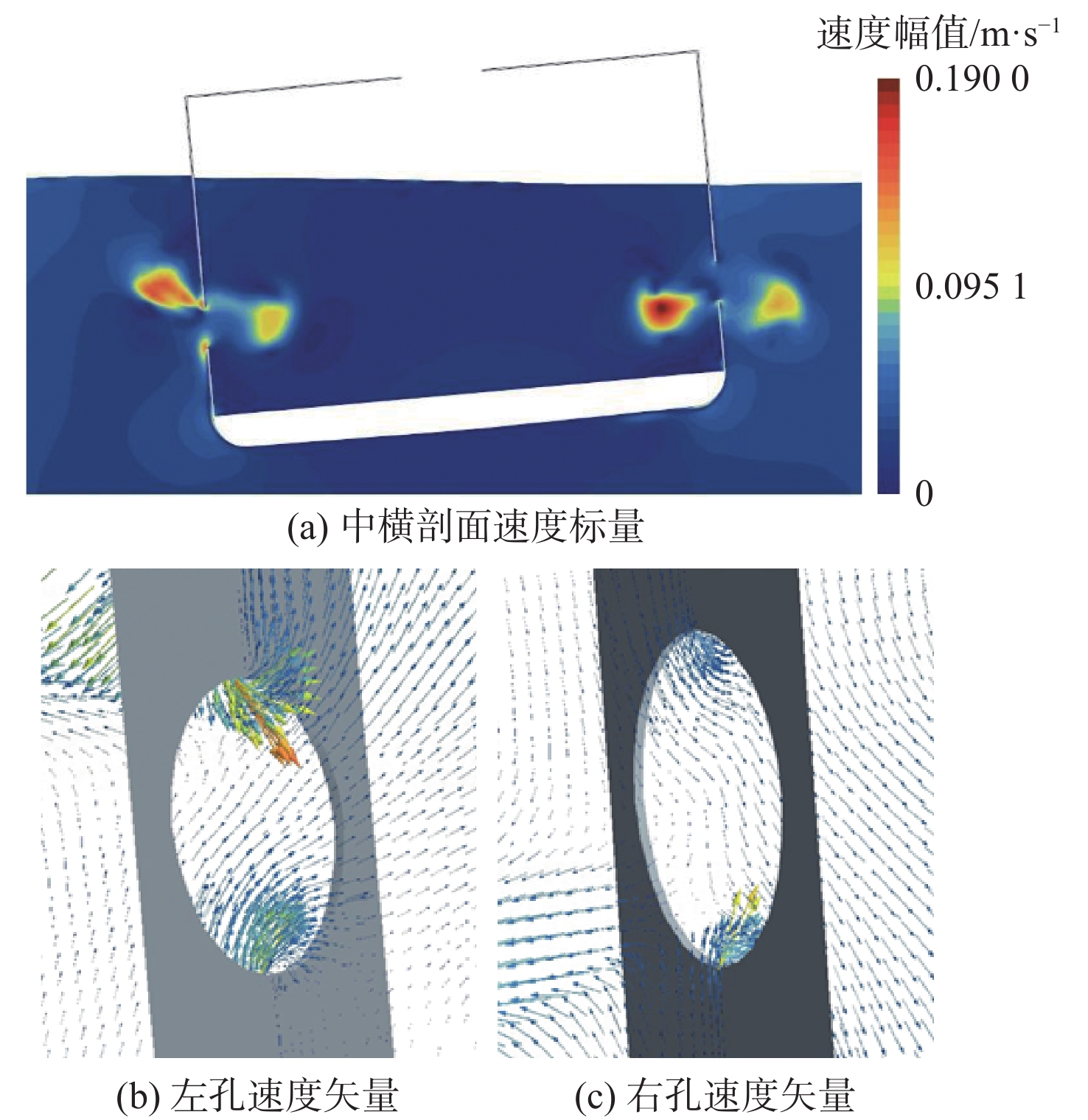
图12为t=1.25 s时的流场状态图，此时船体逆时针横摇的角速度减为0，因此开孔处船体运动诱导产生的水流流量较小。由图12(a)可以看出，船体逆时针横摇时产生的开孔处相对于船体向左运动的水流已大幅衰减，而前半个周期诱导产生的向右运动的水流仍留在开孔附近。由图12(b)和图12(c)可以看出，开孔两侧的速度相反的水流在开孔处相遇，致使开孔处产生漩涡，流线不再光顺，并使水流流量变小。
图13为t=1.75 s时的流场图，此时流场状态与t= 1.25 s时完全相似，只是速度方向相反。
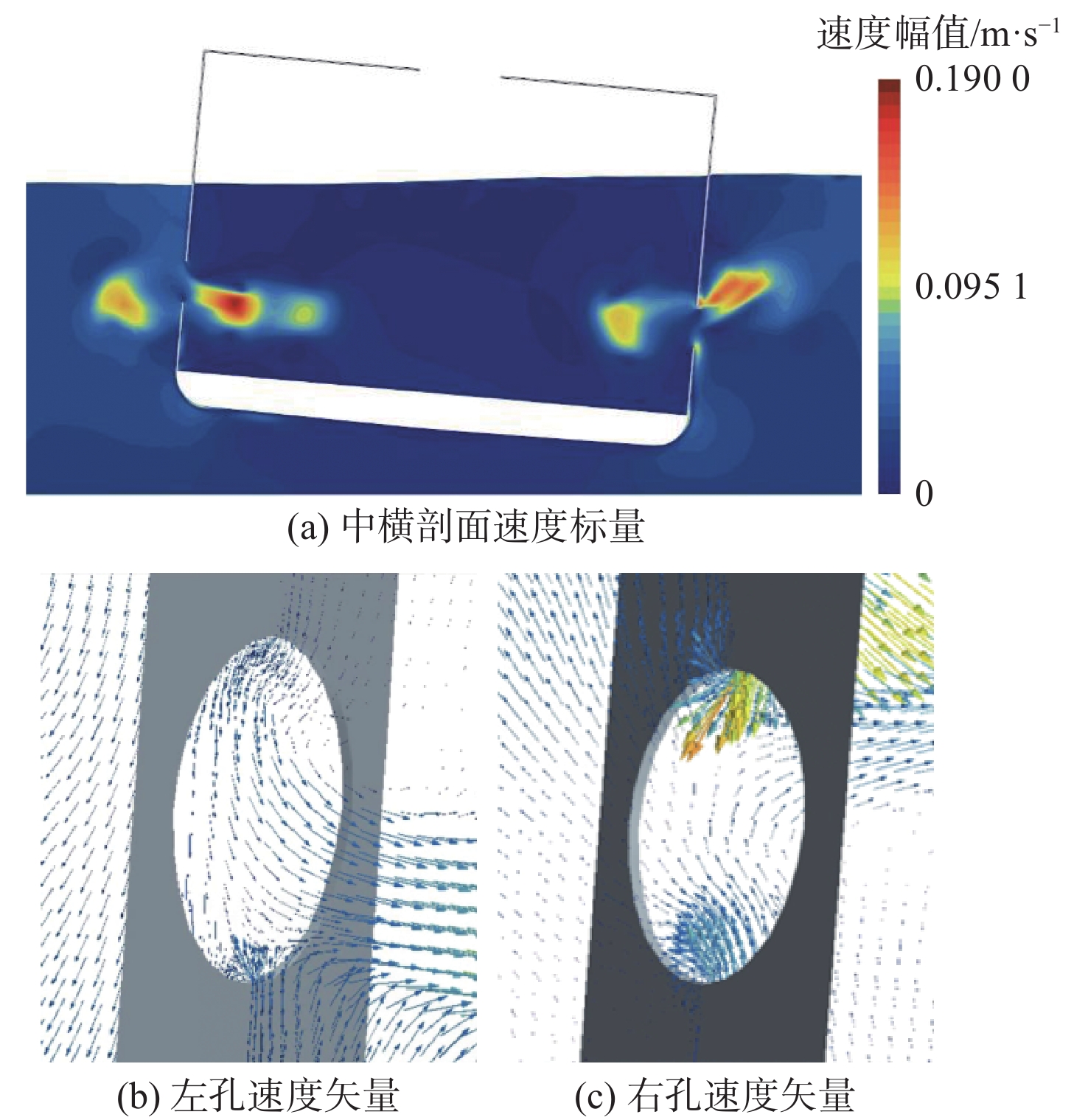
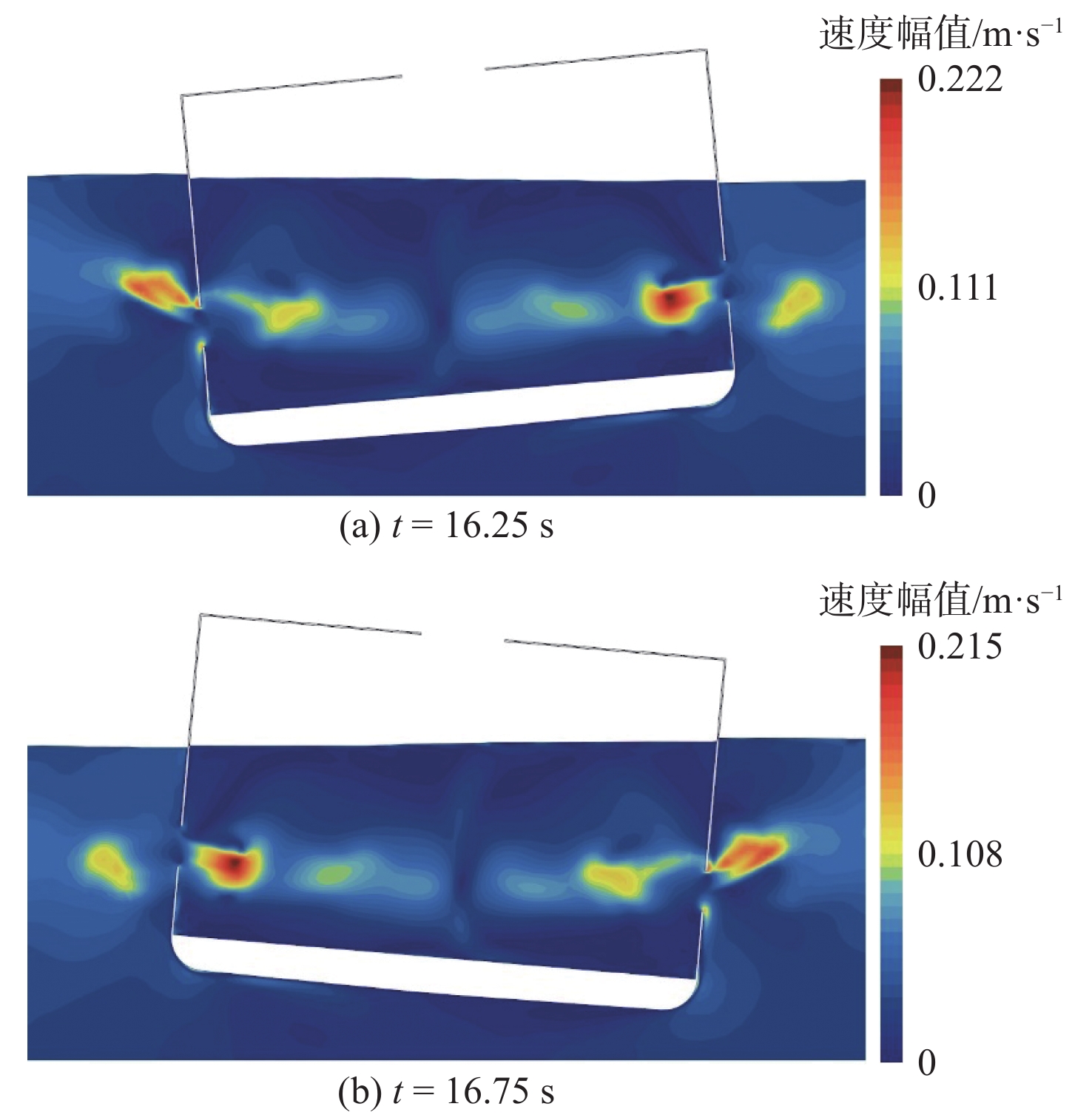
图14为t=16.25和 16.75 s时的速度标量图。随着横摇运动的持续进行，通海液舱附近的流场逐渐进入稳定的周期性变化状态。由于船体横摇运动的诱导和水体自身的惯性影响，开孔处会产生与船体运动方向相反的流体团。两开孔产生的向舱内运动的流体团在运动过程中逐渐衰减，并在船体中横剖面相互抵消，形成一个速度很小的区域。此外，舱内流体团受舱室平底的阻碍作用，呈近似平行于舱底移动。此外，在通海液舱船段进行强迫横摇时，开孔两侧的自由面高度差异很小。因此开孔处水流的主要诱导因素为船体横摇，而非在舱室内外存在较大液面高度差时发挥主要作用的流体静压力。
![]()
图 14 平稳周期变化的中横剖面流速标量图Figure 14. Scalar plot of flow velocity with stable periodic variation in the middle cross-section3.3 不同工况下开孔流速计算与分析
由模拟与分析结果可知，在强迫横摇时，通海液舱船体周围的流场趋于周期性变化。为了更精确分析开孔处水流速度与船体横摇之间的关系，本文对开口处水的质量流量进行了监测。在STAR-CCM+中，通过某面的质量流量定义为
\dot m = \int {\rho {\boldsymbol{v}} \cdot {\text{d}}{\boldsymbol{a}}} = \sum\limits_f {{\rho _f}{{\boldsymbol{v}}_f} \cdot {{\boldsymbol{a}}_f}} (21) 式中：v为流体速度矢量；a为流量所通过的面；f为计算流量的离散面元； {\rho _f} 为流体在面元f处的密度； {{\boldsymbol{v}}_f} 为面元速度矢量； {{\boldsymbol{a}}_f} 为面元面积矢量。
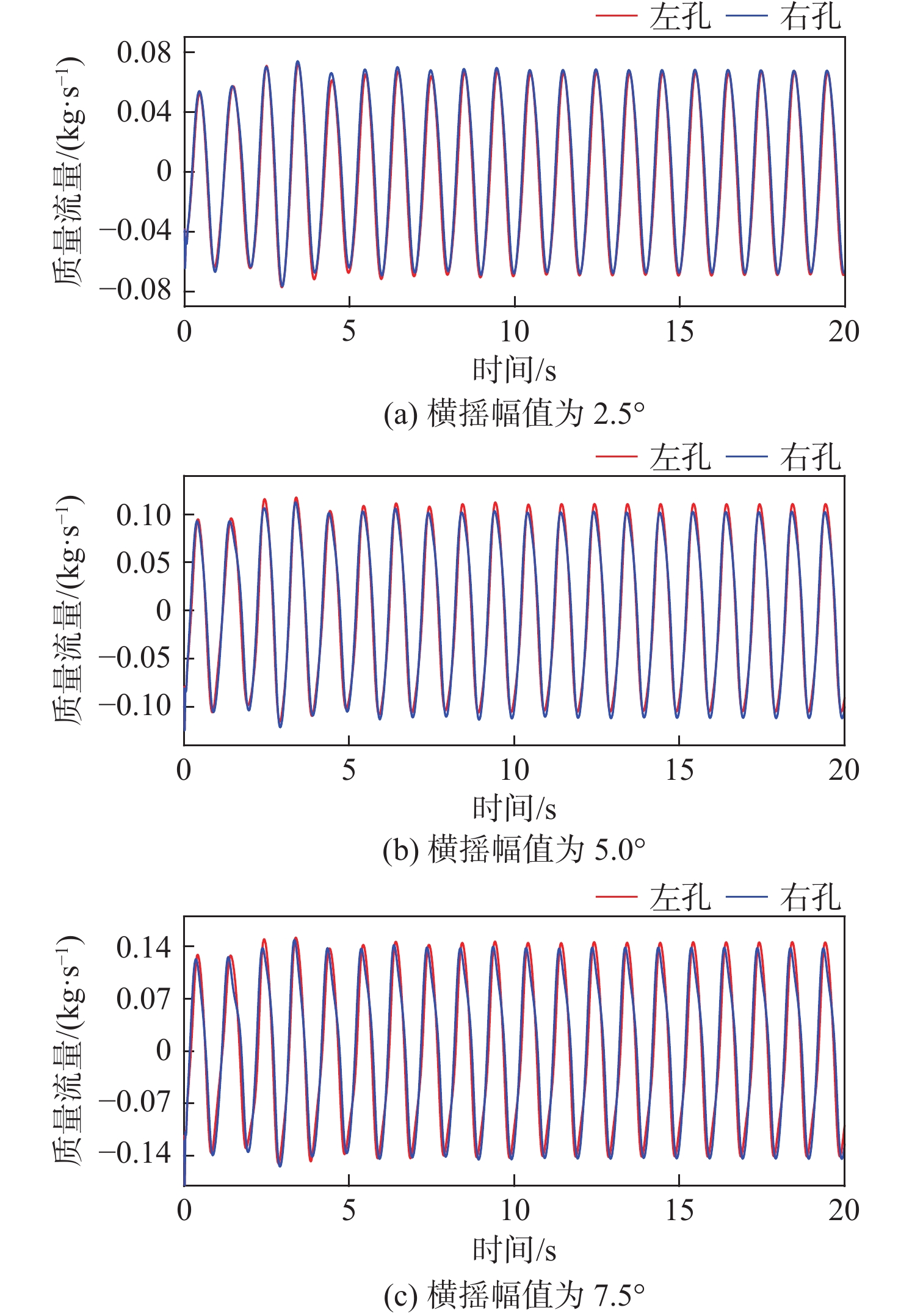
图15为横摇周期为1 s、横摇幅值为2.5°，5.0°，7.5°工况下左右开孔处水流流量的时历曲线。由图可见，经过最初数秒的波动后，开孔处水流变化逐步趋于稳态。由于开孔处水流变化与船体横摇运动密切相关，水体质量流量的时历曲线近似为简谐曲线。随着横摇角的增大，开孔处水流流量的幅值也随之增大，且时历曲线在峰值附近出现一定的变形。此外，左右开孔处的流量方向和大小十分接近，使得在整个变化过程中通海舱内总水量近似恒定。
![]()
图 15 横摇周期为1 s时的开孔流量时历曲线Figure 15. Time history curve of mass flow rate through left/right openings with a rolling period of 1 s为了进一步定量分析通海开孔流量变化，根据其时历曲线特点，运用傅里叶级数对时历曲线进行拟合。CFD计算得到的左右开孔的平均质量流量m(t)可以表示为如下形式：
m(t) = \frac{{{m_0}}}{2} + \sum\limits_{i = 1}^N {{m_i}\cos (i{\omega _{\text{e}}}t + {\gamma _i})} (22) 式中：{m_0}(t)，{m_1}(t)，…，{m_n}(t)为各阶系数，通过整数周期内的数值积分求得；{\omega _{\text{e}}}为船体横摇角频率；{\gamma _n}为各阶分量的相位。
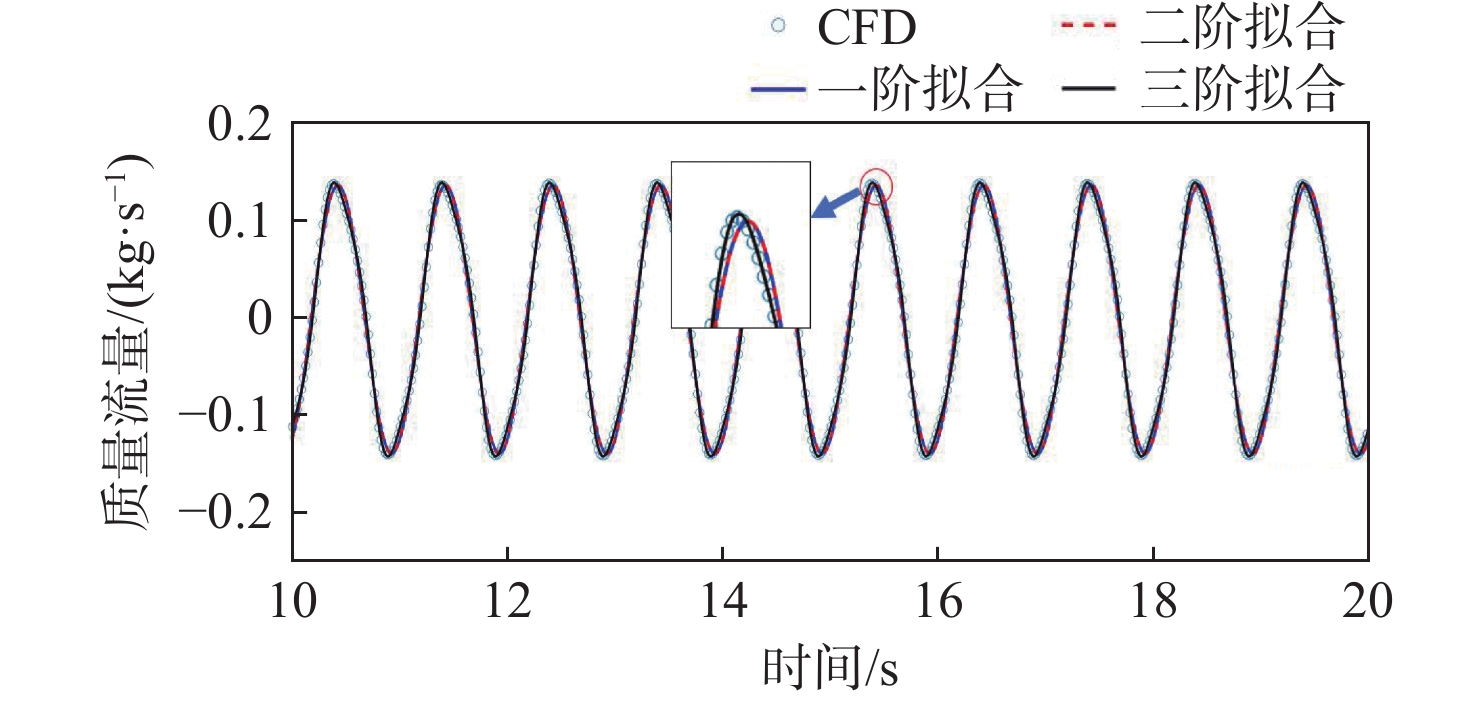
图16所示为各阶Fourier级数对开孔处水流流量的拟合情况。由于水流主要受船体强迫横摇诱导，取到三阶项即可高精度拟合开孔处的水流流量曲线。一、二阶拟合曲线在峰值附近存在少量向右偏移，但峰值大小及峰值以外的曲线部分均能较好地拟合。本文主要保留时历曲线的一阶项，以分析其与船体运动之间的关系。
由前述分析可知，因液舱内外液面高度差很小，所以静水压对开孔处水流形成的影响很小，开孔处水流主要受船体横摇诱导产生。因此使用开孔处船体横摇线速度幅值对水流速度幅值（水流流量除以开孔面积）进行无量纲化处理，以观察不同工况下船体速度与水流速度的关系。
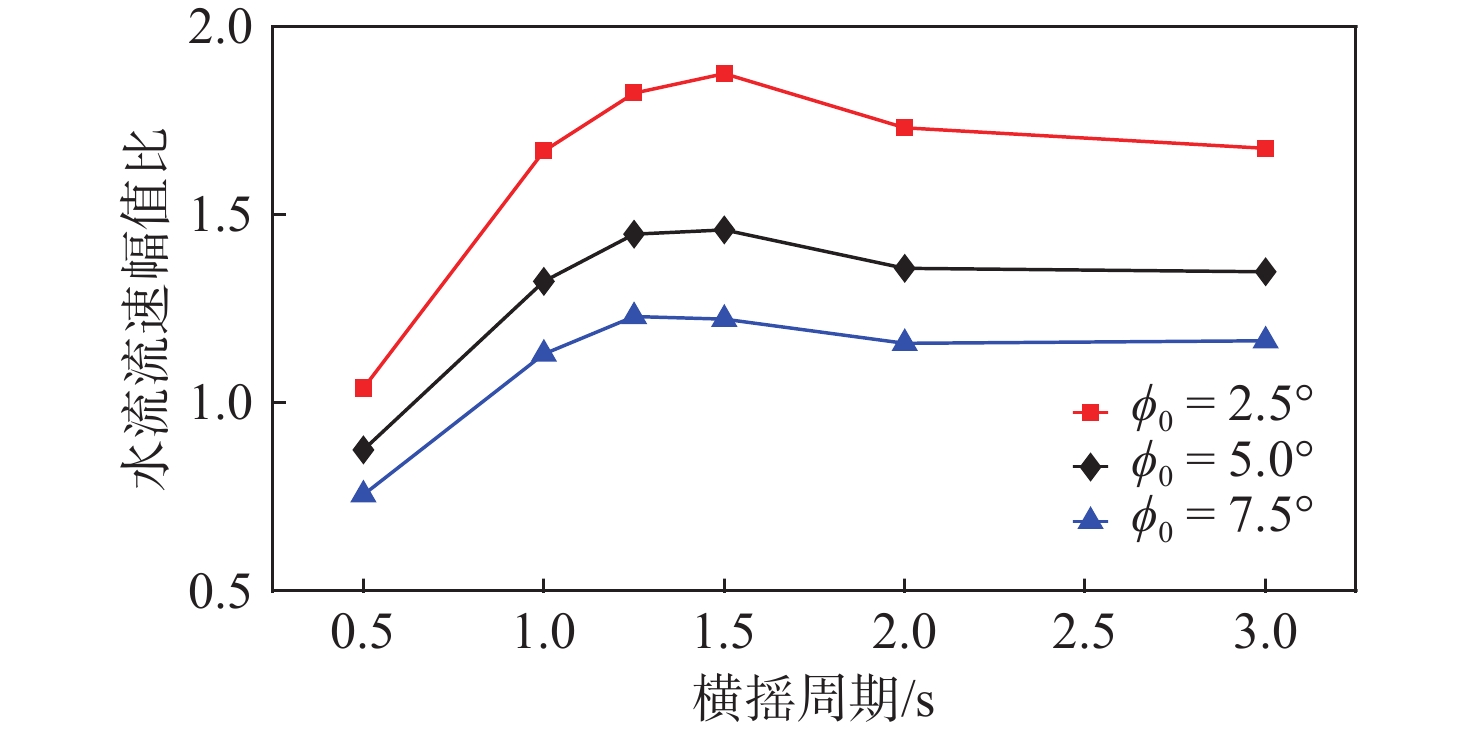
首先分析船体强迫横摇周期和幅值对开孔处水流流量幅值比的影响，如图17所示。由图可见，随着横摇幅值由2.5°增至7.5°，水流流量幅值比逐渐变小，这是因为随着横摇角的增大，横摇速度及诱导的水流速度虽有增大，但开孔处的水流流动阻力也随之增大，导致水流速度增幅小于横摇速度增幅。此外，当横摇周期趋于0时，水流流量幅值比迅速减小。这是由于高频振荡虽会增大横摇速度，但水体的惯性会抑制开孔处水流状态的改变。当横摇周期较大时，水流流量幅值比的变化趋于平缓，这说明船体横摇速度减小时，船体运动对开孔处水体的诱导能力趋于稳定。此外，水流流量幅值比在横摇周期为1.25～1.50 s范围内存在1个峰值，且横摇幅值越大，最大流速出现时的横摇周期越小。
![]()
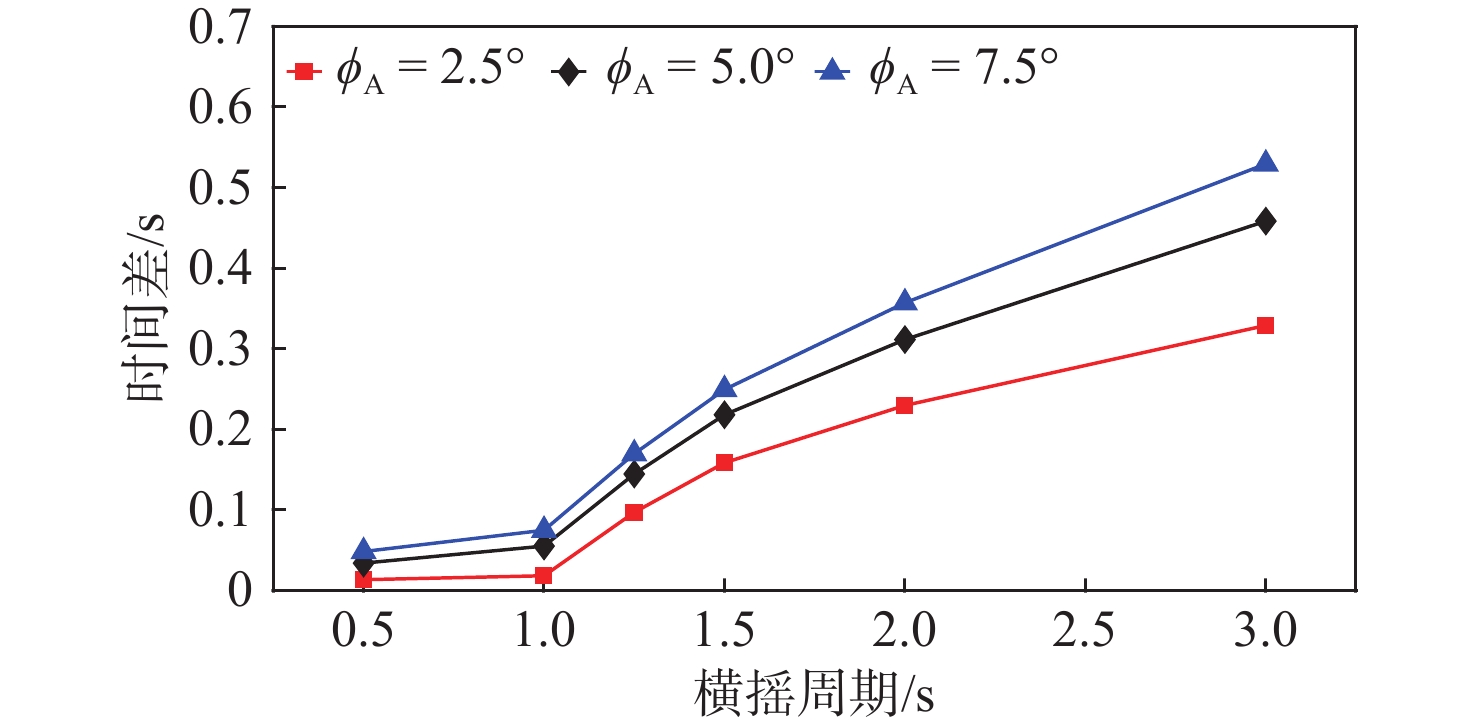
图 17 横摇周期和幅值对开孔处流速幅值比的影响Figure 17. The influence of roll periods and amplitudes on the amplitude of flow velocity amplitude ratio at the opening图18所示为船体强迫横摇周期和速度幅值对开孔处水流速度与船体横摇速度时间差的影响，此处以相位除以角频率表示时间差。结果表明，在选定工况下，两者的时间差均小于船体横摇周期的1/6。在横摇周期由0.5 s变化到3.0 s的过程中，开孔处水流速度相较于船体速度更早达到最大值。这说明当船体运动速度较慢时，船体对开孔处流体的诱导力较弱，导致开孔处水流速度在流经开孔后更快衰减。在横摇幅值由2.5°变化到7.5°过程中，尽管水流速度的幅值增大，但开孔处水流速度的最大值提前出现。这说明较大的横摇角对开孔处水体流动产生了阻碍作用，与图17所反映的趋势一致。
![]()
图 18 横摇周期和幅值对开孔处流量曲线时间差的影响Figure 18. The influence of roll periods and amplitudes on the flow velocity time difference at the opening4. 结 论
本文基于CFD软件对通海型船舶舱段的强迫横摇运动进行了模拟，重点关注开孔附近流场在船体横摇过程中的演化规律，建立了左右舷开圆孔的通海舱段强迫横摇流量监测模型，分析了水流速度与船体运动幅值和周期之间的关系，并对舷侧开孔船段横摇试验数据进行了验证，所得结论如下：
1）运用本文所建立的舷侧开孔强迫横摇数值模型得到的开孔方舱内液面演化的模拟结果与试验数据吻合良好，且在网格和时间步参数均单调收敛。
2）在横摇过程中，左右开孔处的水流流量最终呈现出近似简谐的周期性变化；每个时刻左右孔的水流方向和大小极为接近。当船体横摇速度较大时，诱导的开孔水流速度也较大，反之亦然。
3）由于开孔的阻塞效应，开孔处水流速度总体为船体横摇速度的1～2倍。当横摇幅值增大时，流速幅值比会变小并趋于稳定。较小的横摇周期对开口流量有抑制作用。而当横摇周期为1.0～1.5 s时，流速幅值比存在一极大值，峰值相较于稳态值的增幅约为5.7%～11.0%。
4）开孔处水流速度与船体横摇速度之间存在相位差，且该相位差随横摇周期增大而近似线性增大，约为横摇周期的15%。此外，相位差也随横摇幅值的增大而增大，但增度逐渐趋于平缓。
以上规律可以为通海船舶性能的进一步预报提供参考。
-
![]()
图 4 各网格数下C点处的水位时历曲线
Figure 4. Time history curve of water level at point C under each mesh number
![]()
图 5 各时间步下C点处的水位时历曲线
Figure 5. Time history curve of water level at point C at each time step
![]()
图 6 C点处水位数值计算结果与试验结果的比较
Figure 6. Comparison between the numerical results and experimental results of water level at point C
![]()
图 7 破损舱室强迫横摇中横剖面液面演化图
Figure 7. The evolution of liquid level in the damaged compartment on transverse section during forced rolling motion
![]()
图 14 平稳周期变化的中横剖面流速标量图
Figure 14. Scalar plot of flow velocity with stable periodic variation in the middle cross-section
![]()
图 15 横摇周期为1 s时的开孔流量时历曲线
Figure 15. Time history curve of mass flow rate through left/right openings with a rolling period of 1 s
![]()
图 17 横摇周期和幅值对开孔处流速幅值比的影响
Figure 17. The influence of roll periods and amplitudes on the amplitude of flow velocity amplitude ratio at the opening
![]()
图 18 横摇周期和幅值对开孔处流量曲线时间差的影响
Figure 18. The influence of roll periods and amplitudes on the flow velocity time difference at the opening
表 1 破损舱室模型主要参数
Table 1 Main parameters of the damaged compartment model
参数 数值 舱长L/m 0.386 舱宽B/m 0.345 舱高H/m 0.223 矩形破口尺寸/m 0.074×0.059 通风口尺寸/m 0.072×0.068 吃水d/m 0.095 
下载: 导出CSV
表 2 C点水位时历数值模拟验证结果
Table 2 Verification results of numerical simulation of water level time history at point C
参数 数值 \delta _G^ * /mm 0.661 {U_G} / \bar H /% 1.60 \delta _T^ * /mm 0.165 {U_T} / \bar H /% 0.638 \delta _{SN}^ * /mm 0.826 {U_{SN}} / \bar H /% 1.72
下载: 导出CSV
表 3 C点水位时历数值模拟确认结果
Table 3 Validation results of numerical simulation
参数 数值 {U_G}/\bar H /% 1.60 {U_T}/\bar H /% 0.638 {U_{SN}}/\bar H /% 1.72 {U_V}/\bar H /% 5.29 E/\bar H /% 4.67
下载: 导出CSV
表 4 通海舱段模型参数
Table 4 Model parameters of the ship section
参数 数值 舱长L /m 0.4 舱宽B /m 0.376 舱高H /m 0.230 型深D /m 0.257 圆孔半径r /m 0.015 吃水d /m 0.180
下载: 导出CSV
-
[1] BEGOVIC E, MORTOLA G, INCECIK A, et al. Experimental assessment of intact and damaged ship motions in head, beam and quartering seas[J]. Ocean Engineering, 2013, 72: 209–226. doi: 10.1016/j.oceaneng.2013.06.024
[2] BEGOVIC E, DAY A H, INCECIK A, et al. Roll damping assessment of intact and damaged ship by CFD and EFD methods[C]//Proceedings of the 12th International Conference on the Stability of Ships and Ocean Vehicles. Glasgow: STAB, 2015: 14−19.
[3] BEGOVIC E, DAY A H, INCECIK A. An experimental study of hull girder loads on an intact and damaged naval ship[J]. Ocean Engineering, 2017, 133: 47–65. doi: 10.1016/j.oceaneng.2017.02.001
[4] MANDERBACKA T, RUPONEN P, KULOVESI J, et al. Model experiments of the transient response to flooding of the box shaped barge[J]. Journal of Fluids and Structures, 2015, 57: 127–143. doi: 10.1016/j.jfluidstructs.2015.06.002
[5] RUPONEN P, SUNDELL T, LARMELA M. Validation of a simulation method for progressive flooding[J]. International Shipbuilding Progress, 2007, 54(4): 305–321.
[6] 张相龙, 李廷秋. 基于破损舱室晃荡进水的量化试验研究[J]. 船舶工程, 2023, 45(8): 54–61. doi: 10.13788/j.cnki.cbgc.2023.08.08 ZHANG X L, LI T Y. Quantitative experimental study based on flowing water in damaged cabin[J]. Ship Engineering, 2023, 45(8): 54–61. doi: 10.13788/j.cnki.cbgc.2023.08.08
[7] JASIONOWSKI A. An integrated approach to damage ship survivability assessment[D]. Glasgow: University of Strathclyde, 2001.
[8] SANTOS T A, SOARES C G. Study of damaged ship motions taking into account floodwater dynamics[J]. Journal of Marine Science and Technology, 2008, 13(3): 291–307. doi: 10.1007/s00773-008-0011-8
[9] MACKAY E, SHI W, QIAO D S, et al. Numerical and experimental modelling of wave interaction with fixed and floating porous cylinders[J]. Ocean Engineering, 2021, 242: 110118. doi: 10.13140/RG.2.2.16339.20002
[10] MACKAY E, LIANG H, JOHANNING L. A BEM model for wave forces on structures with thin porous elements[J]. Journal of Fluids and Structures, 2021, 102: 103246. doi: 10.1016/j.jfluidstructs.2021.103246
[11] 卜淑霞, 顾民, 鲁江. 波浪中破损船舶运动的时域预报[J]. 中国造船, 2018, 59(2): 80–89. doi: 10.3969/j.issn.1000-4882.2018.02.009 BU S X, GU M, LU J. Prediction of damaged ship motions in waves in time domain[J]. Shipbuilding of China, 2018, 59(2): 80–89. doi: 10.3969/j.issn.1000-4882.2018.02.009
[12] 卜淑霞, 张培杰, 辜坚, 等. 底部和舷侧破损船舶运动时域预报方法[J]. 中国造船, 2023, 64(1): 224–235. doi: 10.3969/j.issn.1000-4882.2023.01.020 BU S X, ZHANG P J, GU J, et al. Time-domain numerical method for predicting damaged ship motion with side or bottom damaged breach[J]. Shipbuilding of China, 2023, 64(1): 224–235. doi: 10.3969/j.issn.1000-4882.2023.01.020
[13] GU Y. Experimental and numerical investigation on wave-induced loads acting on intact and damaged naval combatant vessel[D]. Glasgow: University of Strathclyde, 2019.
[14] XUE W, GAO Z L, XU S M. Numerical study on attitude and resistance of a side-damaged ship during steady flooding[J]. Journal of Marine Science and Engineering, 2022, 10(10): 1440. doi: 10.3390/jmse10101440
[15] ZHANG A M, CAO X Y, MING F R, et al. Investigation on a damaged ship model sinking into water based on three dimensional SPH method[J]. Applied Ocean Research, 2013, 42: 24–31. doi: 10.1016/j.apor.2013.03.006
[16] GAO Z L, GAO Q X, VASSALOS D. Numerical study of damaged ship flooding in beam seas[J]. Ocean Engineering, 2013, 61: 77–87. doi: 10.1016/j.oceaneng.2012.12.038
[17] 刘闯. 新型养鱼船工作船舱内流场CFD数值仿真研究[D]. 大连: 大连理工大学, 2019. LIU C. Study on CFD numerical simulation of flow field in the working tank of a new type fishing ship[D]. Dalian: Dalian University of Technology, 2019.
[18] ITTC. Uncertainty analysis in CFD verification and validation, methodology and procedures[C]//Proceedings of the 28th International Towing Tank Conference. Wuxi: ITTC, 2017. (查阅网上资料, 未找到本条文献作者信息, 请确认)
[19] 朱德祥, 张志荣, 吴乘胜, 等. 船舶CFD不确定度分析及ITTC临时规程的初步应用[J]. 水动力学研究与进展A辑, 2007, 22(3): 363–370. doi: 10.3969/j.issn.1000-4874.2007.03.015 ZHU D X, ZHANG Z R, WU C S. Uncertainty analysis in ship CFD and the primary application of ITTC procedures[J]. Journal of Hydrodynamics A, 2007, 22(3): 363–370. doi: 10.3969/j.issn.1000-4874.2007.03.015
[20] 吴家俊, 李廷秋, 李杰. 基于CFD的破舱进水数值研究[J]. 中国造船, 2023, 64(2): 25–35. doi: 10.3969/j.issn.1000-4882.2023.02.003 WU J J, LI T Y, LI J. Numerical study on flooding of damaged compartment based on CFD[J]. Shipbuilding of China, 2023, 64(2): 25–35. doi: 10.3969/j.issn.1000-4882.2023.02.003
计量
- 文章访问数: 94
- HTML全文浏览量: 9
- PDF下载量: 22
