0.   引　言

与单体自主水下航行器（AUV）相比，多AUV协同系统具有高效、可靠、灵活等优势^[1-3]。近年来，多AUV协同系统因其在水下攻防、海洋监测、目标探测等重要场景的应用而受到广泛关注^[4-6]。目前常用的编队控制算法主要有：领航者–跟随者法、人工势场法、图论法和基于行为法等^[7-10]。

其中，人工势场法（artifical potential field，APF）是一种利用势场函数在目标空间中建立虚拟力场，从而实现队形自组织、AUV避碰和障碍躲避的典型势场算法^[11]。然而，基于APF的编队控制算法存在一些问题：合斥力与引力等价造成局部最优^[12]、目标太远或距离障碍太近导致引力异常从而造成振荡失效^[13]。对此，付雷等^[14]为解决APF法中的局部最优问题，利用旋转势场以垂直方向吸引个体，确保个体的虚拟合力不为零，从而解决局部最优的问题。张钟元等^[15]针对引力异常造成的振荡失效问题，采用归一化和高阶指数缩放变换来优化引力变化，有效解决引力异常造成的振荡失效问题。然而，大多数关于改进APF的编队控制算法研究考虑得不够全面 ^[14-17]，可能导致这种基于虚拟场的算法不能有效应对其他关于势场算法的问题。因此，有必要引入新的技术以解决这些与势场有关的典型问题。

集群协作在自然界的生物群内部也是一种常见的现象，如候鸟迁徙、鲸群围捕、蜂群筑巢，这些多智能体协同架构能够提高集群协作的性能^[18]。受生物启发的分布式控制利用多个体协作带来的仿生群体优势，提高集群的智能化程度，更好地完成了单体无法完成的工作^[19-20]。近年来，国内外学者针对基于生物启发的分布式水下协同控制技术开展了相关研究工作。例如，谭东旭等^[21]利用神经动力学模型（neural dynamics, ND）构造反步误差，实现编队期望跟踪功能。朱大奇等^[22]利用视觉环境感知设计路径规划算法，实现无需训练的规划模型。上述研究基于简单的启发式规则，在宏观上实现了复杂的群体目标。然而，上述研究并未考虑这种分布式控制环节引入的内部非线性干扰或可能存在的AUV滞回问题。事实上，AUV个体在处理障碍产生的避障路径代价时，需要不断改变跟踪点，当期望收敛速度过快时，上述研究中基于最优方向的策略可能会导致AUV折返或偏离路线，这将加大避障决策带来的路径代价。

此外，海下复杂洋流等不确定因素对AUV的控制存在扰动，各种障碍也可能不同程度地影响编队系统^[23-25]，如沉船等大型障碍或水草等小型障碍。因此在多AUV协同控制系统中，需要针对环境未知扰动以及个体控制系统中协同算法环节引入的非线性干扰，对个体控制律进行优化^[26-28]。田磊等^[26]提出一种能够解决高阶异构集群系统输出时变编队跟踪问题的控制方法，摆脱个体对全局信息的依赖。王浩亮等^[27]基于事件触发机制进行通信资源和机载能量受限条件下多AUV协同路径跟踪控制研究。张兰勇等^[28]针对微小型欠驱动AUV集群控制问题设计一种基于改进RRT*算法的编队控制策略，提高路径规划质量，缩短了集群收敛时间。然而，上述研究中控制器的设计暂未考虑内部非线性因子，在真实的海下环境中，未考虑的外部干扰和其他环节引入的内部非线性干扰也将影响AUV，进而影响协同控制效果。

针对上述问题，本文将以复杂海况下的多AUV分布式编队控制为背景展开研究，提出一种基于神经动力学模型预测（neural dynamics prediction，NDP）的多AUV编队自适应控制方案。针对障碍干扰和避障过程中期望收敛过快造成的AUV滞回问题，设计NDP编队控制算法；并考虑NDP算法环节在系统中引入的未知非线性因子干扰，基于非线性自适应反步法（adaptive back stepping，ABS）设计ABS期望跟踪控制器；同时，利用李雅普诺夫函数证明上述系统的稳定性；最后通过仿真实验验证该方案是否具有有效性与优势。

1.   问题描述

1.1   AUV模型

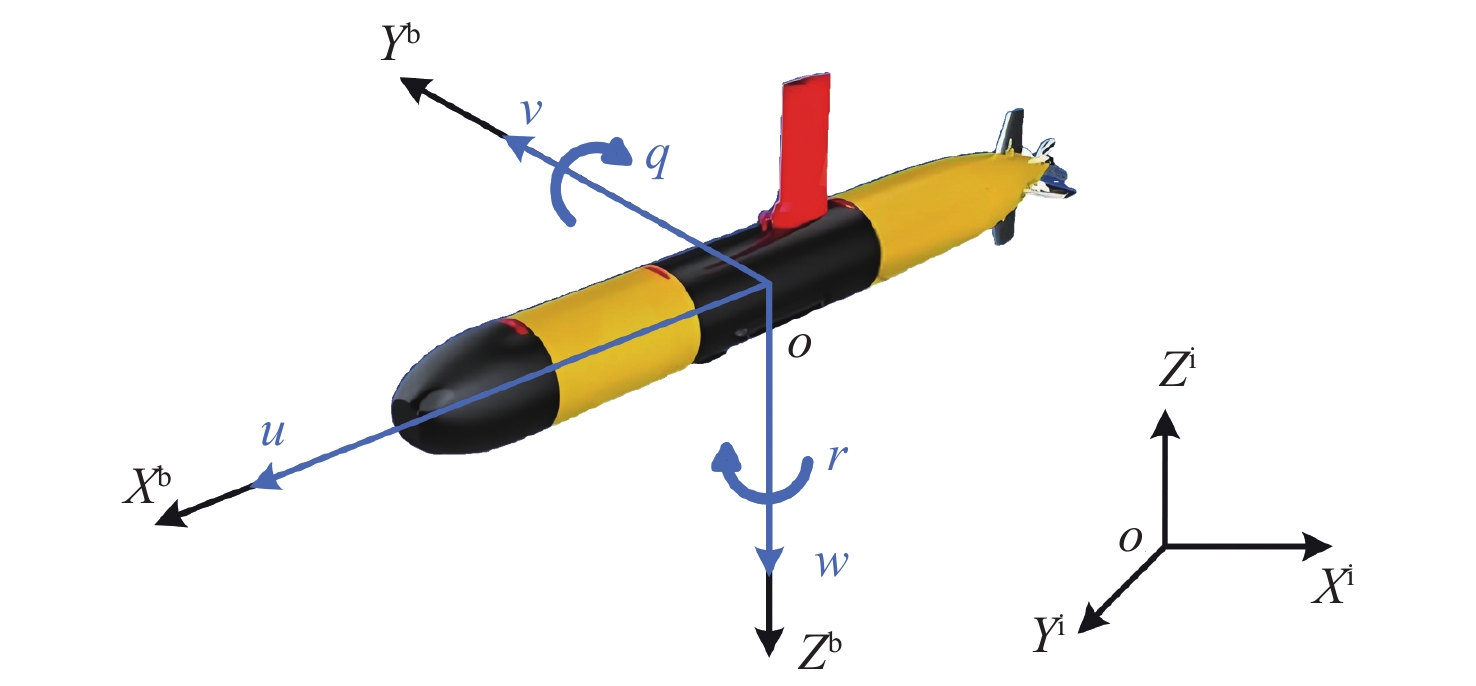
如图1所示，在目标空间中建立惯性坐标系$O - {X^{\rm{i}}}{Y^{\rm{i}}}{Z^{\rm{i}}}$，载体坐标系$O - {X^{\text{b}}}{Y^{\text{b}}}{Z^{\text{b}}}$，其中载体系以AUV浮心为原点，${X^{\rm{b}}}$指向舰首，${Y^{\rm{b}}}$指向右舷，${Z^{\rm{b}}}$指向舰底。

图  1  AUV在惯性坐标系下的定义

Figure  1.  AUV coordinate system definition in inertial frame

下载: 全尺寸图片 幻灯片

AUV在水下的运动近似为弱机动状态，即横滚近似为零，此时系统为五自由度系统，于是载体坐标系下AUV的动力学方程表示为^[29]

式中：M为AUV质量与附加惯性水动力矩阵；C为科里奥利矩阵；D为阻尼矩阵；五自由度状态变量${\boldsymbol{v}} = {[u,v,w,q,r]^{\rm{T}}}$；对应自由度控制输入${\boldsymbol{F}} = {[{F_X},{F_Y},{F_Z},{F_M},{F_N}]^{\rm{T}}}$；${\boldsymbol{g}}(\eta )$为结果近似为零的重力与浮力矢量和。对上式展开得到

式中：m为AUV的质量；${I_y}$和${I_z}$分别为AUV绕${Y^{\rm{b}}}$和${Z^{\rm{b}}}$的转动惯量；$u,v,w,q,r$分别为沿船首方向的纵向速度、右舷方向速度、垂向速度、俯仰角速度和偏航角速度；${{\boldsymbol{X}}_{\dot u}},{Y_{\dot v}},{Z_{\dot w}},{M_{\dot q}},{N_{\dot r}}$为惯性水动力和黏性水动力在对应下标的自由度上造成的附加系数；${\varDelta _u},{\varDelta _v},{\varDelta _w},{\varDelta _q},{\varDelta _r}$为外界扰动以及负载变化造成的未建模的非线性函数项；${F_X},{F_Y},{F_Z},{F_M},{F_N}$为对应下标自由度的控制输入；${F_{{\mathrm{bv}}}}$是与状态相关的非线性项，展开如下：

式中，${z_g}$为角速度导致的水动力系数。则AUV在惯性坐标系下的状态空间模型为：

式中：${{\boldsymbol{x}}_1} = {(x,y,z,\theta ,\psi )^{\text{T}}}$；${\boldsymbol{x}}_{2}$为${{\boldsymbol{x}}_1}$对时间的变化率，${{\boldsymbol{x}}_2} = {(u,v,w,q,r)^{\text{T}}}$；F为控制器输入力矩。

根据实验得到真实海况下的海流性质^[29]，其在重力作用下呈现波动特性，表现为无黏性无回转的表面自由波，于是真实海流的流速场表述为^[29]：

式中：t为自由海流由初始状态变化到目标状态所经历的时间；$k_{\rm{C}}$为海流波数；${\omega _{\rm{C}}}$为波幅角频率；${M_{{\rm{C}}1}}$，${M_{{\rm{C}}2}}$，${M_{{\rm{C}}3}}$为波幅系数，与波幅、海流波高有关。

1.2   控制目标

假设载体坐标系下AUV与期望之间的距离偏差为${\boldsymbol{z}}_{\rm{b}}^{\rm{i}} = ({{\boldsymbol{x}}_{\rm{b}}},{y_{\rm{b}}},{{\boldsymbol{z}}_{\rm{b}}})$，则有

式中：$[{\boldsymbol{\omega}} ]$为AUV绕自转轴旋转角速度r，q的反对称阵；${{\boldsymbol{v}}^{\rm{b}}}$为AUV在载体坐标系下的运动速度；${\boldsymbol{v}}_{\rm{d}}^{\rm{i}}$为AUV在惯性系下的期望速度；${\theta _{\rm{b}}}$和${\varphi _{\rm{b}}}$分别为载体系下AUV姿态角与对应期望${\theta _{\rm{F}}}$和${\varphi _{\rm{F}}}$之间的偏差，并且${\theta _{\rm{F}}}$和${\varphi _{\rm{F}}}$为

${\boldsymbol{R}}({\theta _{\rm{b}}},{\varphi _{\rm{b}}})$为姿态修正矩阵，展开为

于是，控制目标是让偏差渐进收敛至平衡态，而AUV在载体坐标系下与期望的偏差为

2.   NDP-ABS编队控制系统

针对障碍扰动和复杂海况影响AUV编队控制问题，本节提出一种基于神经动力学模型预测的多AUV编队自适应控制方案。

图2为NDP-ABS编队控制系统的结构示意图，图中变量在后文公式中予以解释。系统主要分为NDP编队策略算法环节和ABS轨迹跟踪控制器：前者针对障碍扰动，结合滚动预测给定平滑度较高的AUV期望；后者针对海流和内部非线性因子干扰，为AUV五自由度动力学模型输出合适的控制律。

图  2  NDP-ABS编队控制系统结构示意图

Figure  2.  Structural diagram of NDP-ABS formation control system

下载: 全尺寸图片 幻灯片

2.1   NDP神经动力学模型预测编队策略

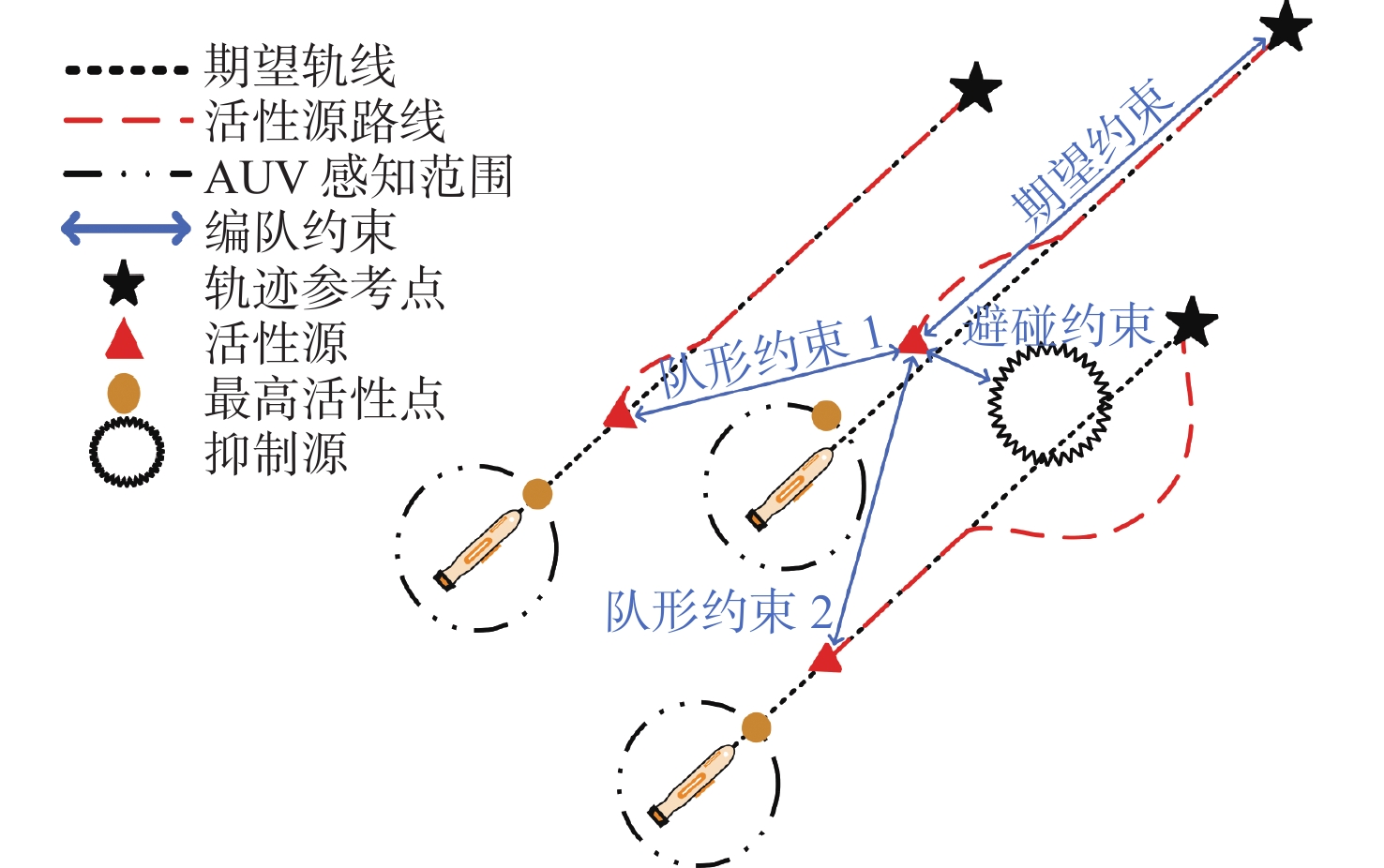
定义集群为${{UV}} = \sum_{n = 1}^N {({{{P}}^n},{{{S}}^n},{{A}}{{{T}}^n},{{H}}{{{P}}^n})}$，其中：$\boldsymbol{\mathit{P}}^n=(\boldsymbol{X}_1^n,\boldsymbol{X}_2^n,\boldsymbol{Z}_1^n,\boldsymbol{Z}_2^n,\boldsymbol{X}_{\rm{1d}}^n,\dot{\boldsymbol{X}}_{\rm{1d}}^n,\ddot{\boldsymbol{X}}_{\rm{1d}}^n)$为${\text{AU}}{{\text{V}}_n}$内部的状态变量；$\boldsymbol{\mathit{S}}^n=(\boldsymbol{p}_s^n,y_s^n)$为${\text{AU}}{{\text{V}}_n}$的活性源；$\boldsymbol{\mathit{A}}\boldsymbol{\mathit{T}}^n= (\boldsymbol{X}_{\rm{1d}}^{AT},\dot{\boldsymbol{X}}_{\rm{1d}}^{AT},\ddot{\boldsymbol{X}}_{\rm{1d}}^{AT},\boldsymbol{p}_{AT}^n,y_{AT}^n)$为${\text{AU}}{{\text{V}}_n}$的期望轨线；$\boldsymbol{\mathit{H}}\boldsymbol{\mathit{P}}^n= (\boldsymbol{p}_{HP}^n,y_{HP}^n)$为${\text{AU}}{{\text{V}}_n}$的最高活性点；${\boldsymbol{p}}_{{s}}^n,{\boldsymbol{p}}_{{AT}}^n,{\boldsymbol{p}}_{{{HP}}}^n$分别为当前时刻对应点的位置；$y_{{s}}^n,y_{{AT}}^n,y_{{{HP}}}^n$分别为当前时刻对应点的神经活性；${\boldsymbol{X}}_{\rm{1d}}^{{AT}},\dot {\boldsymbol{X}}_{\rm{1d}}^{{AT}},\ddot {\boldsymbol{X}}_{\rm{1d}}^{{AT}}$为期望轨线参考点给定的期望；${{H}} = ({\boldsymbol{p}}_{{H}}^j,r_{{H}}^j),j \in {{\bf{N}}_{{H}}}$是抑制源集合。

图3为NDP编队算法原理图，NDP环节作为编队控制系统的核心，利用改进神经动力学方程在目标空间构造神经活性势场，而AUV根据感知范围内的活性分布产出下一步决策，之后采用活性预测算法向ABS控制器输出平滑期望。这种在没有直接队形指令的情况下，通过相互之间的交互和环境的感知，自动地形成并维持所需编队结构的集群控制方式为非显式编队控制。

图  3  NDP编队算法原理图

Figure  3.  NDP formation algorithm schematic diagram

下载: 全尺寸图片 幻灯片

2.1.1   改进神经动力学模型

将三维目标空间栅格化，基于经典神经动力方程^[30]，设计改进神经动力方程为

式中：$y_i$为位于栅格点上神经元i的神经活性；A，B，D分别为活性衰减率、活性上限和活性下限；$In_i^{\text{p}}(t)$为该神经元在t时刻的激励输入；$In_i^{\text{n}}(t)$是该神经元在t时刻的抑制输入。

引理1　通过定义激励输入、抑制输入和内部神经连接，活性源和抑制源的神经活性分别保持在动态活性场的峰值和低谷，可以保证神经活性具有上下界^[30]。

在NDP编队策略下的改进神经动力方程中，激励输入和抑制输入设计如下：

式中：函数${[a]^ + } = \max \{ a,0\} ,{[a]^ - } = \min \{ a,0\}$；K为神经元i周围神经元的数量，且$K \leqslant 26$；$\omega _{ij}^{S}$，$\omega _{ij}^{H}$分别为活性连接权值和抑制连接权值；T为神经元i的状态：活性源、抑制源或非源性神经元。

活性源表征为：个体${\text{AU}}{{\text{V}}_i}$具有的受期望、障碍和其他${\text{AU}}{{\text{V}}_j}$活性源约束的可移动源。其能通过活性连接权值$\omega _{ij}^{S}$影响周围神经元的活性。

抑制源表征为：实体障碍在目标空间中所占据的神经元。其能够通过抑制连接权值$\omega _{ij}^{H}$影响周围神经元的活性。

上述提出的改进神经动力学模型为AUV集群编队控制构建活性势场的基础。神经元拓扑空间中神经活性的影响方式是通过$\omega _{ij}^{S}$和$\omega _{ij}^{H}$实现链式传递，即源性神经元能够通过影响周围非源性神经元的活性来实现活性的链式传递。这种传递方式的运算负担很大，为便于仿真和硬件实现，这里给出NDP模型的另一种形式。

1） 对于活性源，其神经活性为$y_i^S=B$；

2） 对于抑制源，其神经活性为$y_i^H=D$；

3） 对于非源性神经元，其活性计算式为

式中：$K_{S}$为活性源数量；$K_{H}$为抑制源数量；$\left|\left|i,\ j_{S}\right|\right|$（$\left|\left|i,\ j_{H}\right|\right|$）为神经元与活性源（抑制源）的欧几里得距离。非源性神经元的活性计算式通过将链式活性传递转为逐级活性传递，即非源性神经元的神经活性仅需要计算源性神经元的影响。在仿真或硬件实现中对上式进行离散化可以得到NDP模型的解析式，方便活性的计算和迭代。

2.1.2   活性源代价约束

改进神经动力学模型在目标栅格空间中构建了一个动态的活性势场，AUV个体需要在自身感知范围内选择最高活性点作为下一时刻运动期望点，进而跟踪活性源。因此，为实现动态避障、编队控制和期望跟踪，对活性源的移动构造代价函数为

其中包含3个代价约束：

1） 避碰约束。

式中：${N_2}$为实体障碍的数量；${d_{i,{{o}}}}$为活性源与障碍间的距离；${R_{{H}}}$为极限避障距离。当活性源靠近障碍时，该代价将指数增大。

2） 期望约束。

3） 队形约束。

式中，$d_{ij}^{\rm{FM}}$为活性源i与活性源j的期望队形距离，即${\text{AU}}{{\text{V}}_i}$与${\text{AU}}{{\text{V}}_j}$的期望距离。

对于活性源的移动，其将选择代价最小的目标位置作为移动方向。对于${\text{AU}}{{\text{V}}_i}$，其将在感知范围内探测到的活性最高点作为下一时刻的期望位置。

2.1.3   基于模型的活性预测算法

基于改进神经动力学模型构造的动态活性势场，利用3个约束条件使活性源的移动决策产生避障、编队和跟踪效果，最终使AUV个体决策出最高活性位置。

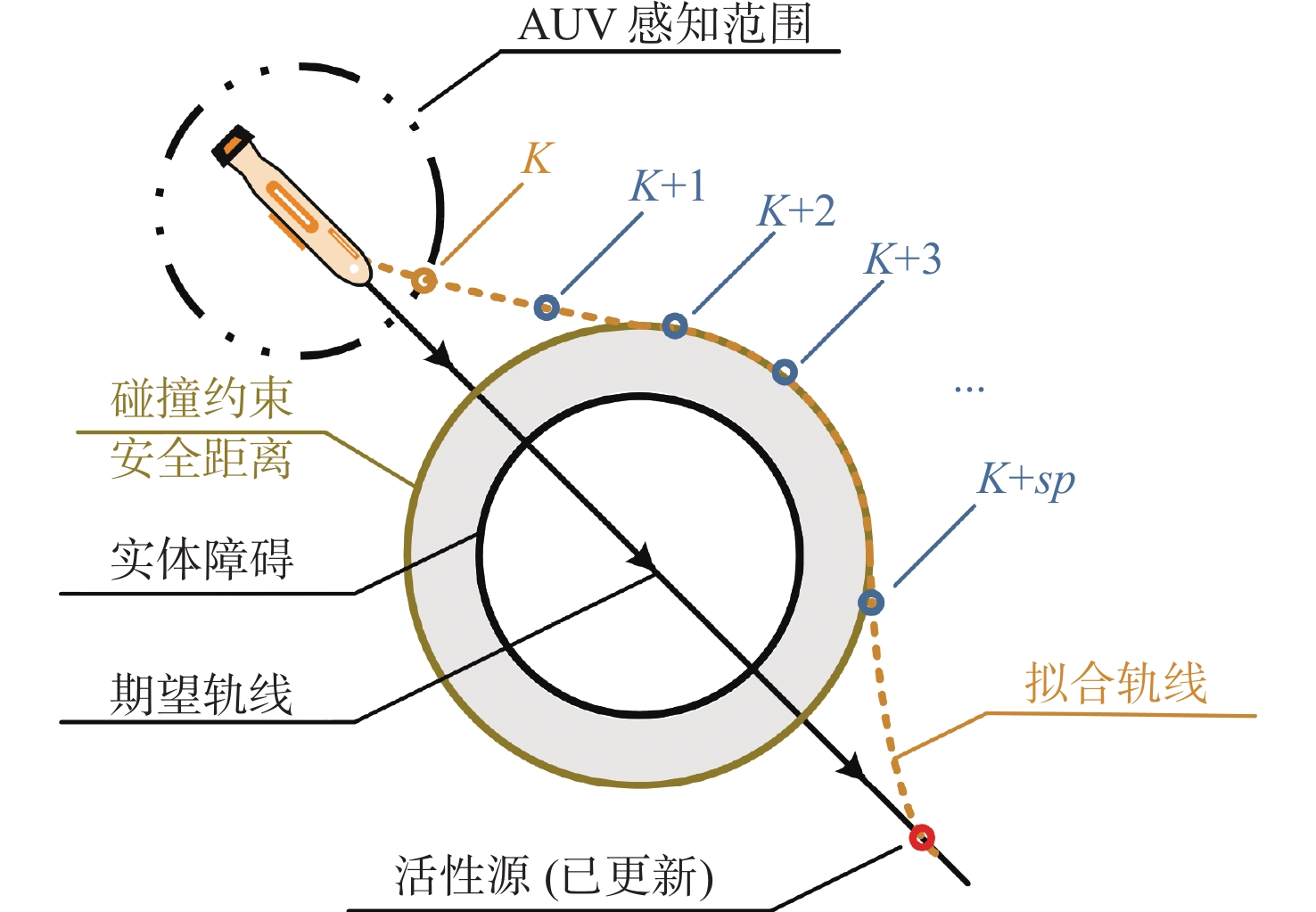
控制律的期望输入维度更高，如果仅输入三维度的位置期望，会导致期望收敛速度过快，进而出现AUV滞回现象，使避障决策造成的路径代价加大，这将对AUV造成严重的安全问题。

对此，引入活性预测算法，在有限的预测步长内对最高活性点的位置进行预测，得到期望位置序列后对预测轨迹进行拟合。取拟合轨线初始点的3个期望特征${\boldsymbol{X}}_{\rm{1d}}^{AT},\dot {\boldsymbol{X}}_{\rm{1d}}^{AT},\ddot {\boldsymbol{X}}_{\rm{1d}}^{AT}$作为最终的控制律输入，从而给定更优的期望输入。

图4为活性预测算法的原理图，假设预测步长为$sp$，于是在$k,k + 1,k + 2, \cdots ,k + sp$时刻，预测的最高活性点位置序列为

图  4  活性预测算法原理图

Figure  4.  Diagrammatic representation of the activity prediction algorithm

下载: 全尺寸图片 幻灯片

式中：$\boldsymbol{p}_{HP}^{ }(k)$为k时刻最高活性点的位置；$\boldsymbol{p}_{HP}^{ }(k+1|k)$为${\text{AU}}{{\text{V}}}$在k时刻下的$\boldsymbol{p}_{HP}^{ }(k)$位置对k+1时刻进行最高活性点预测的位置。以此类推，可以得到最高活性点位置序列。

假设$\varGamma (x,y,z)$是序列点$\boldsymbol{p}_{HP}^{ }$拟合后的轨线，则$\text{AU}\text{V}_{ }$在下一时刻做出决策时，采用轨线$\varGamma (x,y,z)$中$\boldsymbol{p}_{HP}^{ }(k)$处的$\boldsymbol{X}_{\rm{1d}}^{ },\dot{\boldsymbol{X}}_{\rm{1d}}^{ },\ddot{\boldsymbol{X}}_{\rm{1d}}^{ }$期望数据作为控制律的输入。

2.2   轨迹跟踪控制器设计

针对海流干扰和NDP环节在AUV控制系统中引入的非线性因子，基于自适应非线性反步法设计轨迹跟踪控制器输出合适的控制律u，使偏差${\boldsymbol{z}}$收敛。

根据基本状态空间方程式（4），得到系统的状态空间模型为

式中：${{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2} \in {{\bf{R}}^5}$为载体系内AUV位置与速度的状态变量；${\boldsymbol{f}}({{\boldsymbol{x}}_2}) \in {{\bf{R}}^5}$为科里奥利力矩阵项与阻尼矩阵组成的AUV动力学特性参数；${\boldsymbol{\varTheta}} \in {{{\bf{R}}}^{5 \times 5}}$代表参数估计对角矩阵，与AUV载荷改变等相关；${\boldsymbol{\theta}} \in {{{\bf{R}}}^5}$为矩阵${\boldsymbol{\varTheta}}$的对角线元素；非线性项$\varDelta ({{\boldsymbol{x}}_1})$描述海流对AUV运行的干扰，$\varDelta ({{\boldsymbol{x}}_2})$描述运行中位置动态干扰量。

对于未知非线性因子的约束形式主要有如下形式。

引理2　${\varDelta _i}$存在与上一时刻系统状态唯一相关的已知线性上界的约束函数${\delta _i}$，使得$\left| {{\varDelta _i}} \right| \leqslant {\delta _i} (i = 1, \cdots ,n)$成立，或${\varDelta _i}$存在未知常上界参量${D_i}$，使得${\varDelta _i} \leqslant {D_i}$成立^[31]。

引理 3　对于实对称正定矩阵${\boldsymbol{A}} \in {{\bf{R}}^{n \times n}}$，以及非零向量${\boldsymbol{z}} \in {{\bf{R}}^n}$，总有以下不等式成立^[32]：

式中：${\lambda _{\min }}({\boldsymbol{A}})$与${\lambda _{\max }}({\boldsymbol{A}})$分别是对称阵A中最小和最大特征值；${\left\| {\boldsymbol{z}} \right\|^2}$是${\boldsymbol{z}}$的二范数，即$\left\| {\boldsymbol{z}} \right\| = \sqrt {{{\boldsymbol{z}}^{\rm{T}}}\boldsymbol{z}}$。

根据引理2，考虑更加宽松的约束形式，同时引入与${{\boldsymbol{x}}_i}$相关的连续函数${{\boldsymbol{\beta}} _i}$，使${\varDelta _i} \leqslant {{\boldsymbol{\beta}} _i}(i = 1, \cdots ,n)$成立。为实现控制目标，即扰动项$\varDelta ({{\boldsymbol{x}}_1}),\varDelta ({{\boldsymbol{x}}_2})$存在的条件下使误差${\boldsymbol{z}}$收敛，从而保证编队稳定：

式中，${{\boldsymbol{z}}_2} = {\dot {\boldsymbol{z}}_1}$。假设函数${V_1} = {\left\| {{{\boldsymbol{z}}_1}} \right\|^2}/2$，则有

式中：${\boldsymbol{\alpha}}$为用于平滑控制器的虚拟控制量，并且系统参数${k_i},{\varepsilon _i} > 0$。于是，根据引理2可得

${\dot {\boldsymbol{z}}_{\mathbf{2}}}$展开为

假设${\boldsymbol{\theta}}$是未知参量的真实值，其估计值为$\hat {\boldsymbol{\theta}}$，则估计误差$\tilde {\boldsymbol{\theta}} = {\boldsymbol{\theta}} - \hat {\boldsymbol{\theta}}$。$\hat {\boldsymbol{\varTheta}}$表示参数矩阵的估计值，其主对角线元素与$\hat {\boldsymbol{\theta}}$相同。令控制律${\boldsymbol{u}} = {{\boldsymbol{M}}^{ - 1}}{\boldsymbol{F}}$，设计全局李雅普诺夫函数如下：

式中，${\boldsymbol{\varGamma}}$为正定矩阵。结合式（22）和式（23），可得

根据引理2，同理可得

最终，得到控制律u和参数更新项${\mathbf{\hat {\boldsymbol{\theta}} }}$如下：

3.   稳定性分析

从轨迹跟踪问题的现实意义及引理1可知，输入ABS轨迹跟踪控制器的期望输入${{\boldsymbol{x}}_{\rm{d}}}$及其高阶导数是有界的。同时由于受状态约束限制，状态${{\boldsymbol{x}}_1}$，${{\boldsymbol{x}}_2}$存在且有界，故控制律u存在且有界。

接下来将对NDP-ABS系统的稳定性进行分析，并证明系统在合适控制律u输入下，系统状态${{\boldsymbol{x}}_1}$，${{\boldsymbol{x}}_2}$有差跟踪期望轨迹${{\boldsymbol{x}}_{\rm{d}}}$。

定义 1　对于非线性系统

式中：x为系统n维状态变量；u为系统m维控制输入。并且f为${{\bf{R}}^n} \times {{\bf{R}}^m} \to {{\bf{R}}^n}$，是一个连续非线性向量函数的变化矢量。

引理 4　考虑由定义1确定的非线性系统，存在连续的正定标量函数$V(x,t)$，满足

式中：$\xi$为定常系数，与能量函数的收敛速度相关；$M_1$为对估计参数$\boldsymbol{\theta}$的补偿；$M_2$为估计误差补偿项，与状态${\boldsymbol{x}}$的各阶状态有关。$\xi,M_1,M_2 > 0$，使下式成立^[31]：

由式（25）和式（27），可得

对于估计参数${\boldsymbol{\theta}}$：

令状态相关项为${M_1},{M_2}$：

于是式（28）变为

假设能量函数为$V = {\left\| {{{\boldsymbol{z}}_1}} \right\|^2} + {\left\| {{{\boldsymbol{z}}_2}} \right\|^2} + {\tilde {\boldsymbol{\theta}} ^{\rm{T}}}{{\boldsymbol{\varGamma}} ^{ - 1}}\tilde {\boldsymbol{\theta}}$，函数${\gamma _1} = \max \{ 1/2,1/2\lambda ({\boldsymbol{\varGamma}} )\}$，${\gamma _2} = \min \{ {k_i},q/2\}$，其中，$\lambda$为矩阵${\boldsymbol{\varGamma}}$的最小特征值，则由引理3可知

根据${\dot V_2} \leqslant - {\gamma _2}{V_2}/{\gamma _1} + {M_1} + {M_2}$，令${\gamma _2}/{\gamma _1} = \xi$，由引理4得到

在有限时间t内，可知${V_2}$是${{\boldsymbol{z}}_1}$二范数的界，又由于${V_2}$存在上界，故${{\boldsymbol{z}}_1}$满足如下不等关系：

从而得到约束变量的上界关系式

从上式可以发现，通过设置合适的系统参数可以有效减小误差的上界约束值，即${\gamma _1} = 1/2$时，${\gamma _1}({M_1} + {M_2})/{\gamma _2} \geqslant ({M_1} + {M_2})/2{\gamma _2}$成立。

1） 当${k_i} < q/2$时，

2） 当${k_i} \geqslant q/2$时，

由于${M_2}$可以通过设置${\varepsilon _i}$来保证其为较小值，故下界约束值主要由${M_1}$确定，由此得到：

综上所述，控制器在合适参数下是稳定的。

4.   仿真分析

本节设置了6组仿真场景，以验证NDP-ABS编队方案中NDP编队算法和ABS轨迹跟踪控制器的有效性，同时与经典反步编队方案（ND-BS）进行对比，说明其抗扰动性能。

4.1   仿真环境建立

设定仿真时间为100 s，仿真步长为0.01 s，集群数量为3，活性源移动距离为0.01，活性衰减率$A = 0.9$，活性上限$B = 100$，活性下限$D = - 100$，活性连接权值$\omega _{ij}^{\text{d}} = 0.9$，抑制连接权值$\omega _{ij}^{\text{o}} = 0.1$。AUV质量与附加惯性水动力矩阵M为单位阵E，AUV零平面工作深度为150 m。设定系统参数${k_i} = 1$，${\varepsilon _i} = 1$，正定阵${\boldsymbol{\varGamma}}$为单位阵E。设定期望轨线为相同纵深的阿基米德螺线，队形默认为等边三角队形，AUV间的编队保持距离为$\sqrt 3$ m。则${\text{AU}}{{\text{V}}_i}$期望轨迹如下，其中$i = 1,2,3,i \in {\boldsymbol{UV}}$。

设海流波幅${A_{\rm{CR}}} = {10^{ - 3}}\ {\mathrm{m}}$，海流波长$L_{\rm{CR}}=100 \ {\mathrm{m}}$，当地重力加速度$g = 9.8\;{\text{m/}}{{\text{s}}^2}$。设定真实值${\boldsymbol{\theta}}$为${(1.63,1.29, - 1.22,0.58,0.26)^{\text{T}}}$，初始估计值${{\boldsymbol{\theta}} _0}$为$(1.3,1.5, - 1.5,0.2,0.2)^{\text{T}}$，于是非线性因子$\varDelta ({{\boldsymbol{x}}_1}),\varDelta ({{\boldsymbol{x}}_2})$定义为：

4.2   无海流干扰下编队控制过程

无海流干扰条件下，测试正常环境和极端环境下NDP-ABS方案的编队情况。其中，正常环境不设置障碍，极端环境设置若干障碍，并将NDP-ABS方案与ND-ABS方案进行对比，测试NDP编队算法在无海流条件下的有效性。

4.2.1   无海流干扰下正常环境编队过程

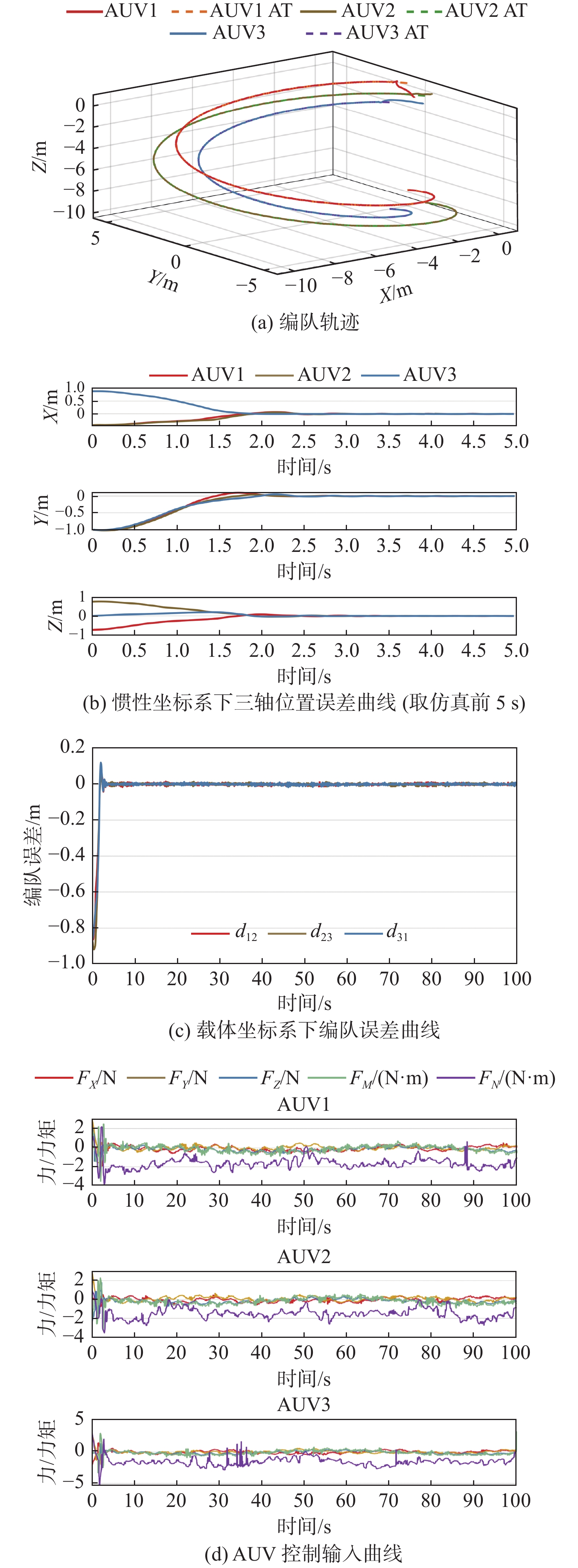
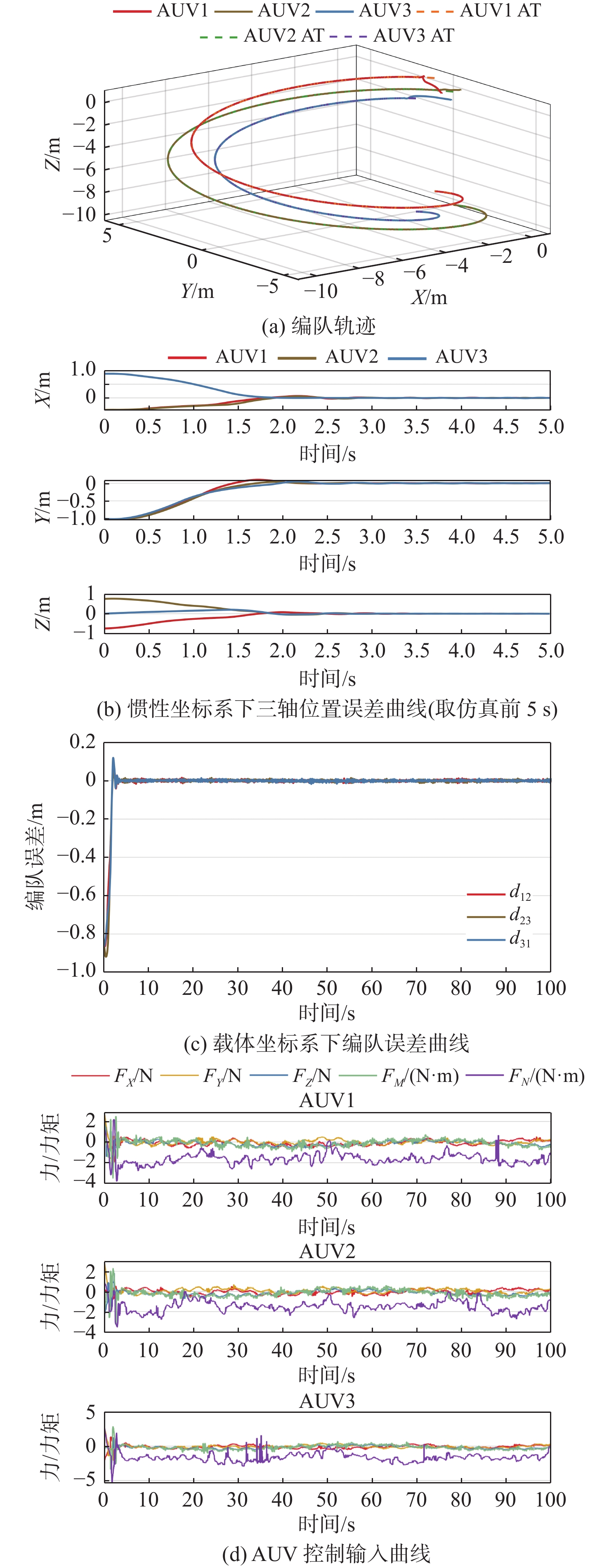
正常环境下NDP-ABS方案和ND-ABS方案编队仿真结果如图5和图6所示，两图分别给出编队轨迹、三轴位置误差、队形误差和不同AUV经过平滑处理后的控制输入变化。图5（a）和图6（a）的实线代表AUV的真实轨迹，虚线代表人为设定的轨迹；图5（c）和图6（c）中${d_{ij}}$表示${\text{AU}}{{\text{V}}_i}$与${\text{AU}}{{\text{V}}_j}$之间实际距离与期望距离的差值。

图  5  NDP-ABS在无海流干扰下正常环境编队仿真结果

Figure  5.  Simulation results of normal formation process of NDP-ABS without current interference

下载: 全尺寸图片 幻灯片

图  6  ND-ABS在无海流干扰下正常环境编队仿真结果

Figure  6.  Simulation results of normal formation process of ND-ABS without current interference

下载: 全尺寸图片 幻灯片

由对比可知，在无海流、无障碍干扰下，NDP-ABS方案和ND-ABS方案均能有效跟踪给定的期望轨线，且二者在载体坐标系下的三轴位置误差及编队误差能够快速收敛。由此验证了NDP-ABS编队方案在无海流、无障碍干扰下的有效性。

4.2.2   无海流干扰下极端环境编队过程

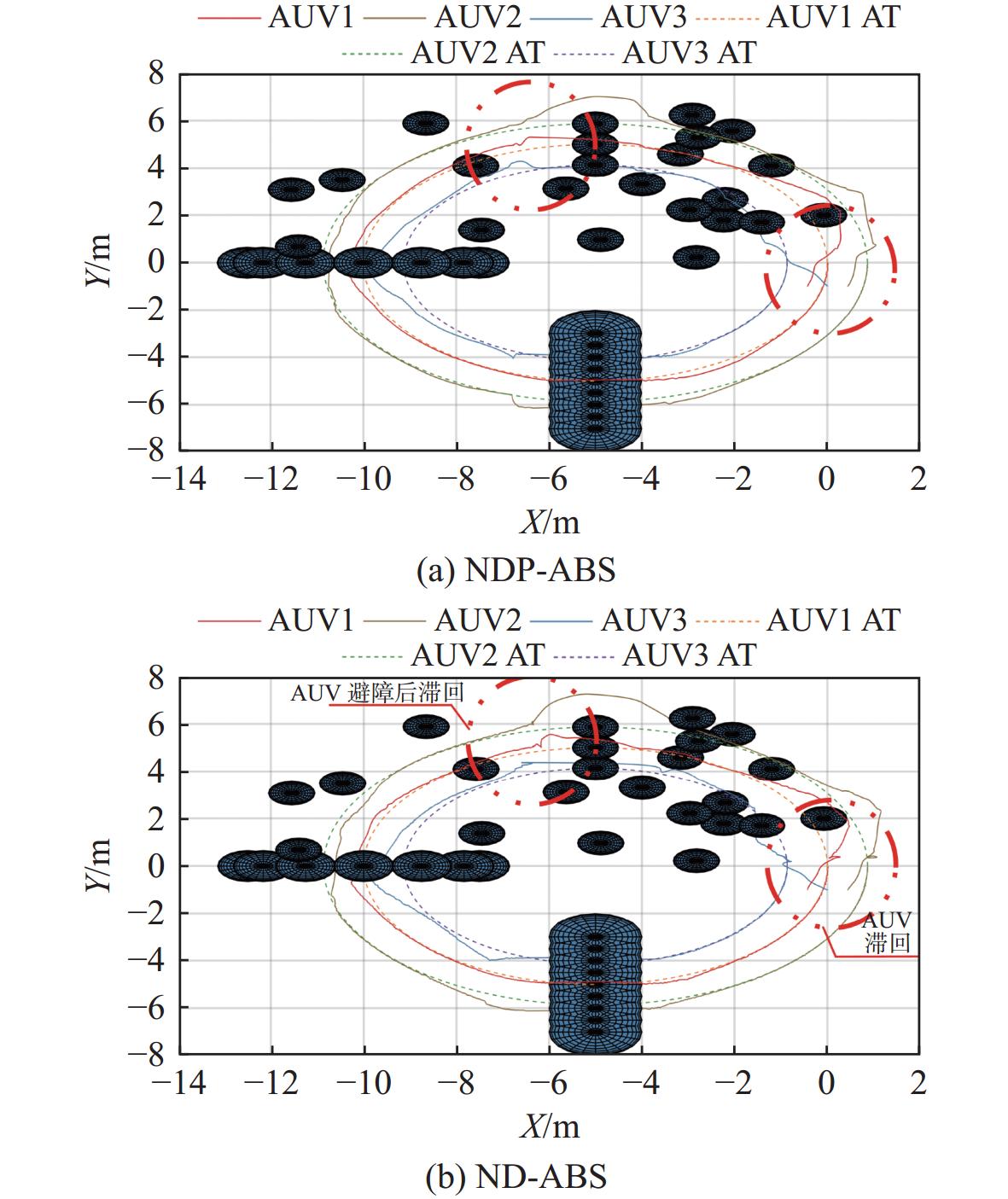
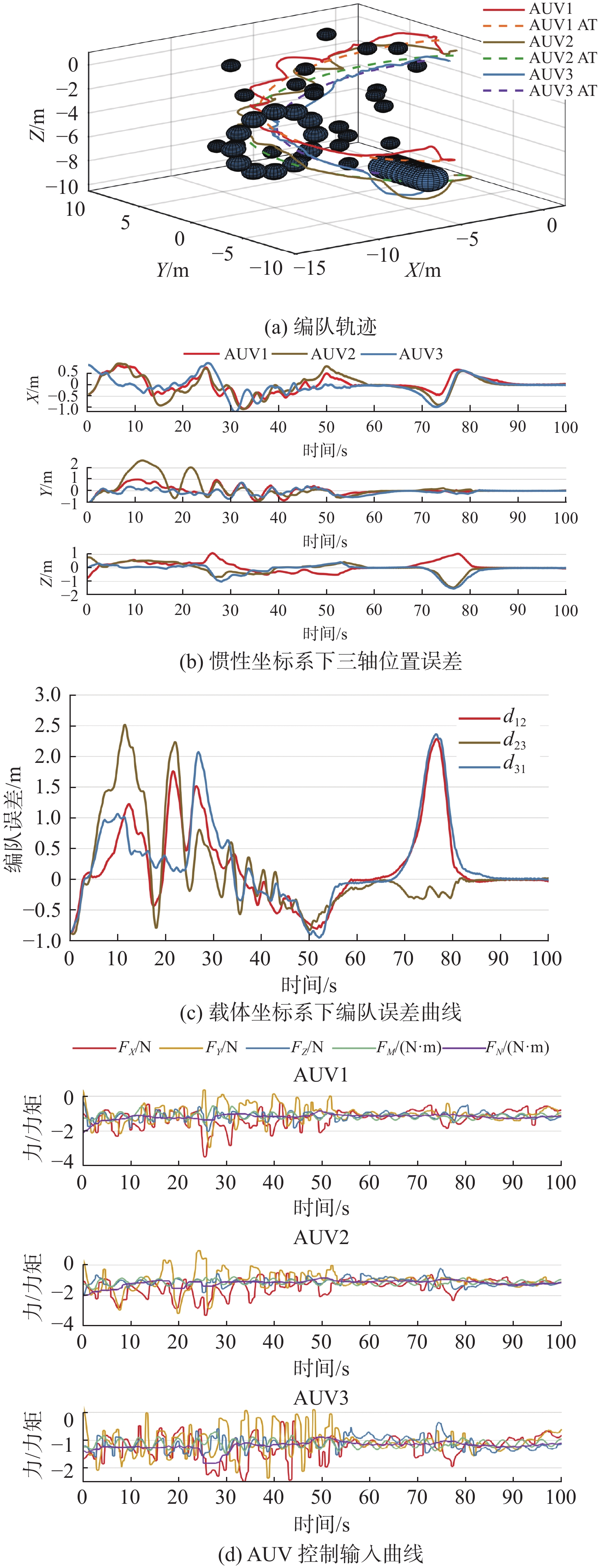
极端环境下NDP-ABS方案和ND-ABS方案编队仿真结果如图7和图8所示，其中${d_{i,{\mathrm{OBS}}}}$表示${\text{AU}}{{\text{V}}_i}$与最近障碍的距离。仿真时在AUV行进路线上设置了一定数量、大小不一的球形障碍，具体包括轨道障碍、环形球体障碍、条形大型障碍和20个随机小型球体障碍。

图  7  NDP-ABS在无海流干扰下极端环境编队仿真结果

Figure  7.  Simulation results of extreme formation process of NDP-ABS without current interference

下载: 全尺寸图片 幻灯片

图  8  ND-ABS在无海流干扰下极端环境编队仿真结果

Figure  8.  Simulation results of extreme formation process of ND-ABS without current interference

下载: 全尺寸图片 幻灯片

由对比可知，两个方案均能有效跟踪期望轨线，在遇到障碍时，载体坐标系下的编队误差会有较为明显的变化，两方案均未与障碍相碰。

对图7（a）和图8（a）中的轨迹进行研究，情况分别如图9（a）和图9（b）所示，ND-ABS方案在规避轨线球体障碍后出现较为明显“折返”现象，本文称为AUV编队滞回现象。而NDP-ABS方案在同样规避后并未出现滞回现象。其原因是ND-ABS方案缺少活性预测，造成AUV期望收敛过快，进而导致避障过快的AUV为减小与其他AUV的队形误差而产生折返决策，最终造成了更高的避障代价。

图  9  无海流有障碍干扰下轨迹俯视图

Figure  9.  Top view of the route with obstacles interfering and without ocean currents

下载: 全尺寸图片 幻灯片

由此可见，NDP算法较经典ND算法具有编队更平滑、避障代价更低的优势。

4.3   海流干扰下编队控制过程

在有海流干扰条件下，测试正常环境和极端环境时NDP-ABS方案的编队情况，正常环境和极端环境设置条件与4.2节一致，并将NDP-ABS方案与NDP-BS方案进行对比。其中，设置正常环境组的目的是测试ABS轨迹跟踪控制器的期望跟踪能力；设置极端环境组的目的是测试当海流干扰和障碍扰动同时存在时，NDP-ABS方案的有效性。

4.3.1   海流干扰下正常环境编队过程

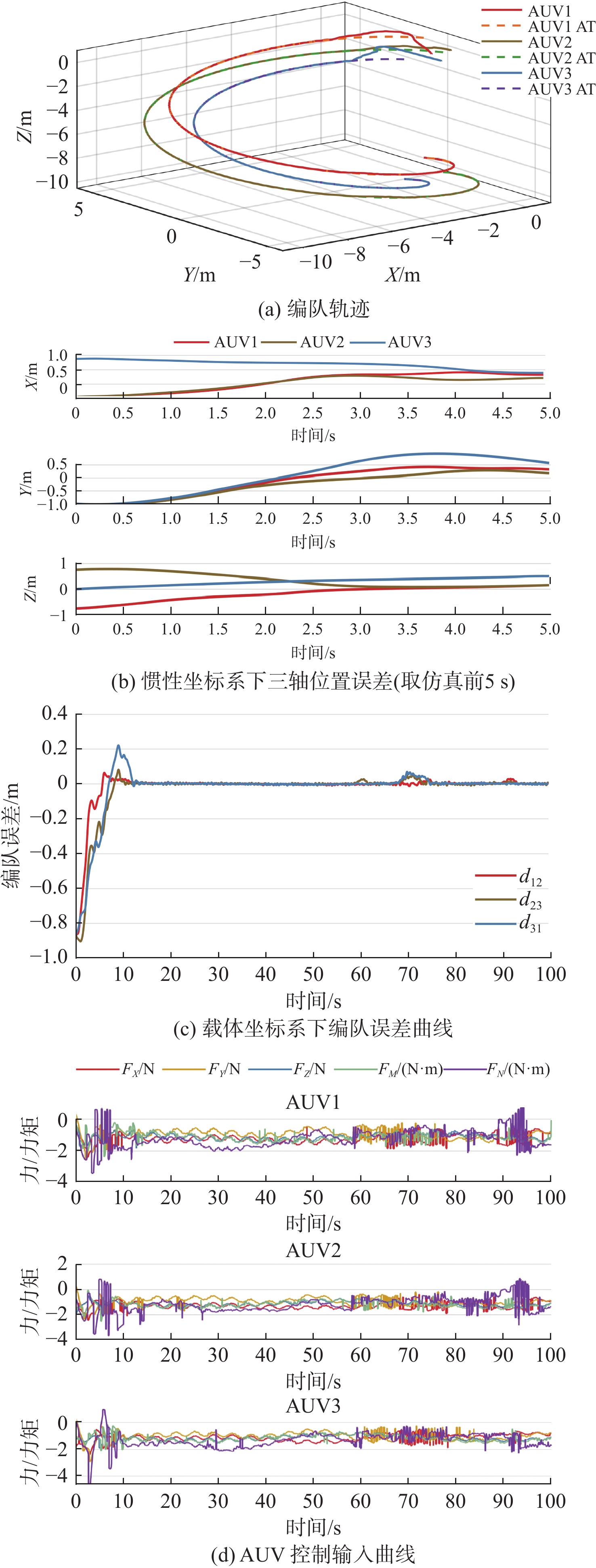
正常环境下NDP-ABS方案和NDP-BS方案编队仿真结果分别如图10和图11所示。两方案均使用NDP编队决策算法进行期望决策产出，但二者采用不同的控制器，其中后者采用基于经典反步法的轨迹跟踪控制器。

图  10  NDP-ABS在海流干扰下正常编队仿真结果

Figure  10.  Simulation results of normal formation process of NDP-ABS under current interference

下载: 全尺寸图片 幻灯片

图  11  NDP-BS在海流干扰下正常编队仿真结果

Figure  11.  Simulation results of normal formation process of NDP-BS under current interference

下载: 全尺寸图片 幻灯片

根据前文给定的海流干扰模型，不同深度的海流扰动不相同，由图10和图11对比可知，在海流干扰存在的情况下，NDP-BS方案在进行轨迹跟踪时受海流扰动影响较大，在前期形成队形过程中出现衰减振荡，当编队误差收敛至稳态后，能够较为稳定地跟踪期望。而NDP-ABS方案并未出现持久的振荡，在快速形成三角队形后稳定跟踪期望轨线。

由对比可知，ABS轨迹跟踪控制器较经典反步控制器具有更强的抗干扰能力；同时也说明了NDP-ABS方案在海流干扰环境下具有较强的稳定性。

4.3.2   海流干扰下极端环境编队过程

极端环境下NDP-ABS方案和NDP-BS方案编队仿真结果分别如图12和图13所示。

图  12  NDP-ABS在海流干扰下极端编队仿真结果

Figure  12.  Simulation results of extreme formation process of NDP-ABS under current interference

下载: 全尺寸图片 幻灯片

图  13  NDP-BS在海流干扰下极端编队仿真结果

Figure  13.  Simulation results of extreme formation process of NDP-BS under current interference

下载: 全尺寸图片 幻灯片

受障碍干扰，AUV需要产出避障决策，因此避障的有效性以及编队稳定性是研究的重点。表1给出了编队过程相关的指标，其中，距离障碍最小值是3台AUV在编队过程中距离障碍最近距离的平均值，表征系统避障的有效性；编队误差方差表征系统编队的稳定性；避障路径代价是AUV实际运行路程与期望轨线长度之差，综合表征控制器跟踪性能和算法决策的优越性。

表  1  NDP-ABS方案与NDP-BS方案在有海流和障碍环境下编队过程指标对比

Table  1.  Comparison of NDP-ABS and NDP-BS schemes' performance indicators in settings with obstacles and ocean currents

指 标	NDP-ABS	NDP-BS
距离障碍最小值	0.582	0.118
编队误差方差	0.314	0.497
避障路径代价	4.176	10.007

下载: 导出CSV 

| 显示表格

由对比可知，NDP-BS方案由于海流和障碍干扰同时存在，轨迹振荡现象更明显，原因是其控制器不能快速跟踪期望，动态性能较差。NDP-ABS方案能够有效跟踪NDP环节产出的期望，同时编队轨迹更平滑。其中，编队稳定性提高36.8%，避障造成的路径代价减少58.3%。

由此可见，在相同仿真工况下，NDP-ABS方案较NDP-BS方案具有更强的抗干扰能力，系统稳定性更好。同时也验证了NDP-ABS编队方案在海流扰动、障碍干扰以及内部NDP环节带来非线性因子等影响下进行编队控制的有效性。

5.   结　语

本文提出了一种能够在复杂海况和障碍环境下进行的基于神经动力学模型预测的多AUV自适应控制方案（NDP-ABS），即利用改进型神经动力学模型在目标空间构造神经活性场，受期望、障碍和队形约束的活性源能够使虚拟场动态变化，AUV通过感知自身范围内的最高活性点，经活性预测后得到最优期望，最终输入ABS期望跟踪控制器。并且证明了NDP-ABS系统在合适系统参数条件下是稳定的。最后，通过6组仿真场景证明了NDP-ABS编队控制方案的有效性和优势，这对海流和障碍共同干扰条件下多AUV水下非显式编队控制具有一定的参考价值。本文尚未考虑通信时滞对AUV跟踪控制的影响，下一步需要在通信随机时滞条件下研究AUV跟踪期望轨迹的方法。