0.   引　言

现代船舶是一种复杂的交通运输载体。在其推进动力系统、照明系统、通信系统和控制系统等主要运行系统中，均会运用到电机，因此，电机是现代船舶不可或缺的核心部件之一。然而，由于船舶真实运行场景复杂多变且环境潮湿，水分易渗入电机，影响润滑效果，增加摩擦和磨损，导致电机极易发生故障^[1]。而轴承作为电机的核心部件之一，其振动信号包含了大量电机运行信息，如故障频率、转频等。因此，对电机轴承振动信号进行准确的故障诊断，不仅可以识别电机的故障状态，也可以有效预防船舶发生深层故障。

随着信号处理技术的飞速发展，各学者针对轴承振动信号故障特征提取方法的研究从时域^[2]、频域^[3]发展到时频域^[4-6]，增强了故障特征提取的适应性。朱晓强等^[2]通过对轴承振动加速度信号的均方根趋势分析，判断是否存在轴承润滑不良故障。Zheng等^[3]提出一种基于频域的稀疏精英群LASSO去噪（SEGLD）方法，揭示轴承故障信号在频域上的稀疏特性，能够有效提取轴承微弱故障特征。丁殿勇等^[4]通过对原始信号的奇异谱分解进行优化，并根据包络谱峰值指标选择敏感的奇异谱分量，最后利用增强多点最优调整最小熵解卷积（EMOMEDA）有效提取故障特征。薛红涛等^[5]提出一种基于分量加权重构与稀疏非负矩阵分解相结合的故障特征提取方法，对时频能量矩阵进行分解降维，有效提取故障特征。赵一楠等^[6]提出一种自适应窗口旋转优化短时傅里叶变换的变转速滚动轴承故障诊断方法，提高了时频表示的能量集中度，实现变转速工况下滚动轴承的故障诊断。然而，面对复杂的船舶运行场景，其电机轴承振动信号呈现出强干扰、非平稳、非线性等特征，采用上述单一分析域内的故障特征提取方法，仅能从一个角度提取故障特征，难以多角度表征复杂场景下的故障特征。

随着人工智能技术在工业领域的广泛应用，基于机器学习的故障诊断技术也获得迅速发展。王超等^[7]提出一种基于自注意力子域自适应对抗网络的故障诊断方法，利用对抗网络和子域自适应模块来减小不同工况数据在全局域和局部域边缘的分布差异，实验表明该方法能有效识别具有代表性的轴承故障。Song等^[8]提出一种宽卷积核卷积神经网络（WKCNN）模型，该模型无须任何预处理即可从原始振动时域信号中自动提取特征，实现智能诊断。An等^[9]提出一种基于周期稀疏注意力和长短期记忆网络（LSTM）的非均匀轴承振动信号滚动轴承故障诊断方法，该方法具有较高的精度和较简单的结构，利用LSTM提取故障信号中的长期依赖特征，可识别轴承故障状态。An等^[10]提出基于递归神经网络（RNN）的轴承智能故障诊断模型，提高了模型的训练效率和诊断能力，具有较高的精度和较简单的结构。然而，以上神经网络均有训练速度缓慢、计算复杂度过高的缺点，并且没有良好的泛化能力，难以适用于多个运行状态下的船舶轴承故障诊断领域。

极限学习机（extreme learning machine, ELM）是一种新型单层前馈神经网络（ingle-hidden layer feedforward neural-network, SLFN），相较于传统的神经网络，具有训练速度快、泛化能力强和适用于非线性等优点，理论上适用于轴承振动信号故障诊断。Xi等^[11]提出一种基于小波分解和加权排列熵(weighted permutation entropy，WPE)的ELM故障诊断分类方法，能够有效识别非平滑滚动轴承振动信号的轴承故障类型。然而，原始ELM的隐含层权值及阈值是随机产生的，且其内部结构具有一定的复杂性，因此模型参数的设置存在难度，影响模型的泛化能力。

基于上述问题，本文将提出一种基于多域信息融合与改进ELM的船舶电机轴承故障诊断方法。该方法基于综合权重诊断指标（synthetic weight detection index, SWDI）和小波包分解选择高敏感时域特征参数和频域特征参数，进而构建多域特征参数集；进一步利用麻雀搜索算法（sparrow search algorithm, SSA）对ELM网络的模型参数进行优化，搭建改进ELM故障诊断模型，用于船舶电机轴承故障的智能诊断。

1.   相关参数选择与多域特征参数集构建

1.1   时域特征参数选择

采用船舶用电机搭建试验台架，基于该台架试验数据，介绍时域、频域和时频域内特征参数的选择方法。船舶用电机试验台架如图1所示，试验所选电机为QSWP40030 X型永磁无刷直流电机。首先，选用KLS7230S可编程电机控制器，通过终端APP匹配电机。

图  1  船舶用电机试验台架

Figure  1.  Ship motor test bench

下载: 全尺寸图片 幻灯片

如图1所示，采集船舶用电机近端垂直、近端水平和近端轴向的轴承振动信号，设置4种轴承状态，分别为正常状态、外圈故障、内圈故障和滚动体故障。试验中采样频率为12.8 kHz，电机各运行状态的振动信号分别采集15 s，故将各运行状态的振动信号数据以每段4 096个数据点划分，每段信号共分为45组。转速设置为300，500和700 r/min，负载设置为10，20 和30 N·m。

针对船舶电机轴承振动信号非线性的特点，时域内特征参数能够反映信号随时间变化的幅值特性。因此，选择4个典型的时域特征参数：均方根T₁、时域偏度T₂、波形率T₃和时域峭度T₄。

式中：y⁽ⁱ⁾ (i=1,2,…,N)为振动信号序列，N为时域信号点数；$\bar y$和σ分别为信号序列均值和标准差；$y_{\mathrm{h}}^{(j)}$(j=1,2,…,N_h)为振动信号极大值序列；$\bar y_{\mathrm{h}}$为信号极大值序列均值；σ_h为信号极大值序列标准差；$y_{\mathrm{l}}^{(k)}$(k=1,2,…,N_l)为振动信号极小值序列；$\bar y_{\mathrm{l}}$和σ_l分别为信号极小值序列均值和标准差。

上述时域特征参数可以表征丰富的信号信息，但是输入的特征参数过多会使模型的诊断效果变差，模型的泛化能力下降，同时也会增加模型训练和预测的计算量。因此，根据船舶真实运行时电机轴承可能存在的正常或故障状态，基于SWDI值分别评估时域特征参数的敏感度，SWDI值计算公式如下^[12-13]：

式中：μ₁，μ₂分别为特征参数在电机轴承两种不同状态下的均值；σ₁，σ₂分别为对应标准差；N为电机轴承的状态数量，结合船舶用电机试验台架的试验数据，取N=4；R_T为时域高敏感特征参数的数量，需将时域和频域考虑在内，且输入特征参数不宜过多，因此取R_T=1；Q为运行工况的数量，结合采集的试验数据，根据转速共设置9种运行工况，因此取Q=9；设敏感度阈值α=0.95；w为区分度权重系数。

通过计算时域特征参数的SWDI值，选取SWDI值最高的参数作为多域特征参数集的时域高敏感特征。

1.2   频域特征参数选择

轴承振动信号中可能存在的故障成分具有周期性质，而频域特征参数能够分析频谱特征，针对性地发现信号中的周期性故障成分。本文选择频谱歪度F₁、频谱尖度F₂、时间通过率F₃和波形稳定指数F₄作为高敏感频域特征参数的潜在选项：

式中：f_z(z=1,2,…，Z)为振动信号频谱序列，Z为频谱点数；P(f_z)为f_z的频率幅值；σ_f为频谱基准偏差；$\overline f$为频谱序列均值。

取频域高敏感特征参数R_F=1，计算频域特征参数的SWDI值，选取SWDI值最高的一组特征参数，作为多域特征参数集的频域高敏感特征。

1.3   时频域特征参数选择

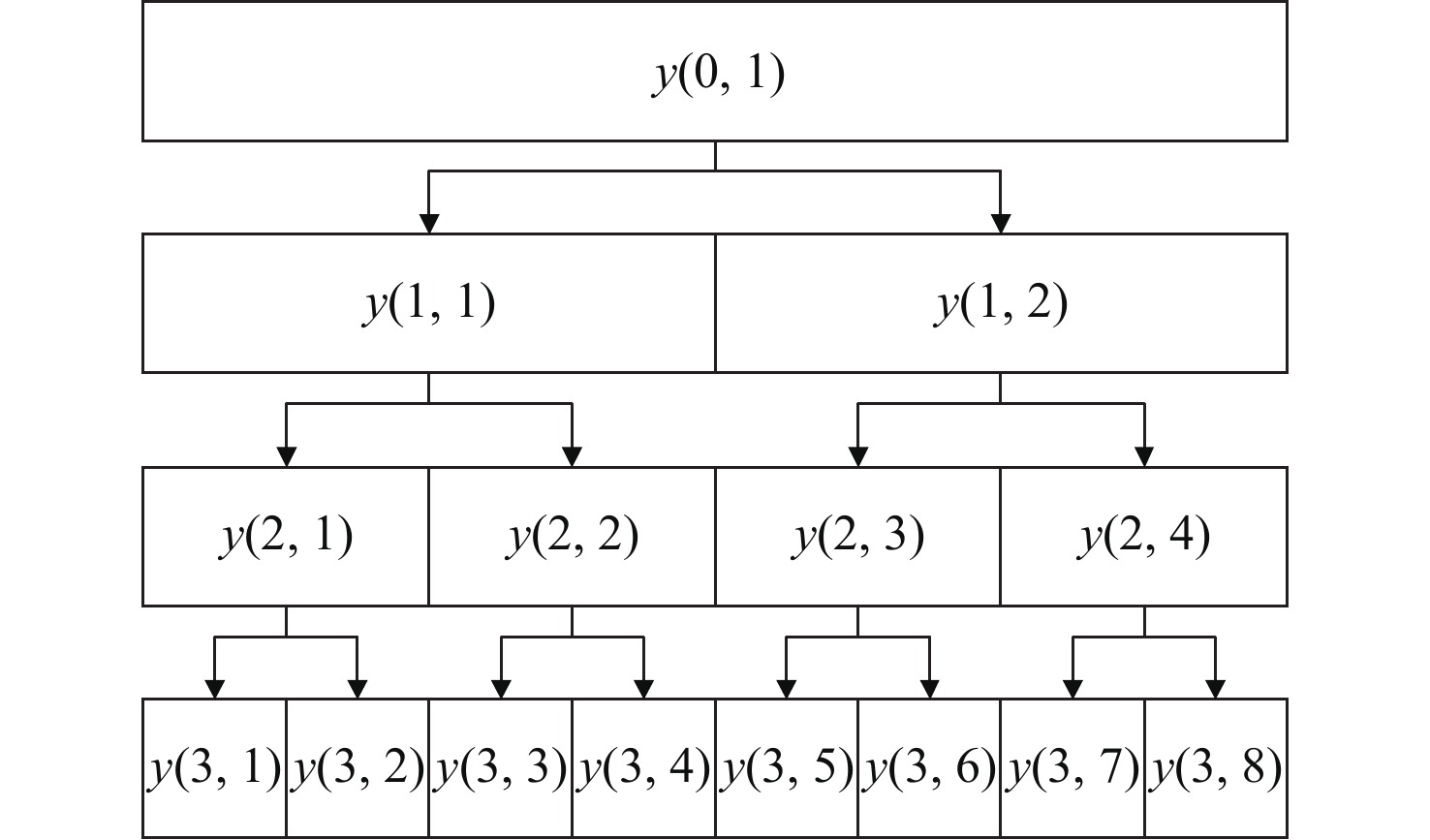
时域特征参数只能反映信号随时域变化的特征，而频域特征参数只能反映信号的频率特性，无法全面表征非平稳轴承振动信号的特征信息。时频域特征参数包含信号时域和频域的信息，能够有效反映信号频谱随时间的变化情况，有利于分析非平稳信号。三层小波包分解能够在时频域之间取得良好的平衡，既能有效捕捉到信号的细节特征，又避免过于复杂的计算。相较于二层分解，三层分解能够提取更多的关键信息，而四层或更多层的分解则可能导致冗余信息的增加，提升计算复杂度。此外，三层小波包分解在处理旋转机械信号时表现出较好的效果，能够有效识别故障特征。因此，本文采用基于三层小波包分解的时频分析方法获取信号时频域特征参数。由于DB3母小波计算复杂度较低^[14]，选用 DB3 小波作为母小波，对原始信号三层小波包分解，其原理如图2所示。

图  2  三层小波包分解原理图

Figure  2.  Schematic diagram of three-layer wavelet packet decomposition

下载: 全尺寸图片 幻灯片

其中，y(0,1)为原始信号，y(a,b)为第a层（a=0,1,2,3）的第b个节点（b=1,2,…,2^a）的小波包分解得到的信号子频带，记第3层子频带能量值为E_i（i=1,2,…,2^a）。进一步地，基于频带能量占比选择占比前三的子频带能量值作为多域特征参数集的时频域高敏感特征参数。

1.4   多域特征参数集构建

基于上述时域、频域和时频域内特征参数的选择方法，构建多域特征参数集，作为后续诊断模型的输入，构建流程如图3所示。

图  3  多域特征参数集构建流程

Figure  3.  Process for constructing multi-domain symptom parameter sets

下载: 全尺寸图片 幻灯片

以船舶用电机试验台架的实验数据为例，采样频率为12.8 kHz，每种运行状态的振动信号采集时长为15 s。将每段信号按4096个数据点划分，共分为45组进行分析。基于此计算时域特征参数与频域特征参数的SWDI值，如表1所示。

表  1  各特征参数的SWDI值

Table  1.  SWDI values of each symptom parameter

分析域	特征参数	SWDI值
时域	T1	1 215.3
	T2	871.3
	T3	748.8
	T4	759.7
频域	F1	381.3
	F2	317.2
	F3	1 488.5
	F4	375.0

下载: 导出CSV 

| 显示表格

从表1可以看出，T₁在时域内的SWDI值最高，F₃在频域内的SWDI值最高，故选择T₁和F₃分别作为时域和频域高敏感特征参数。

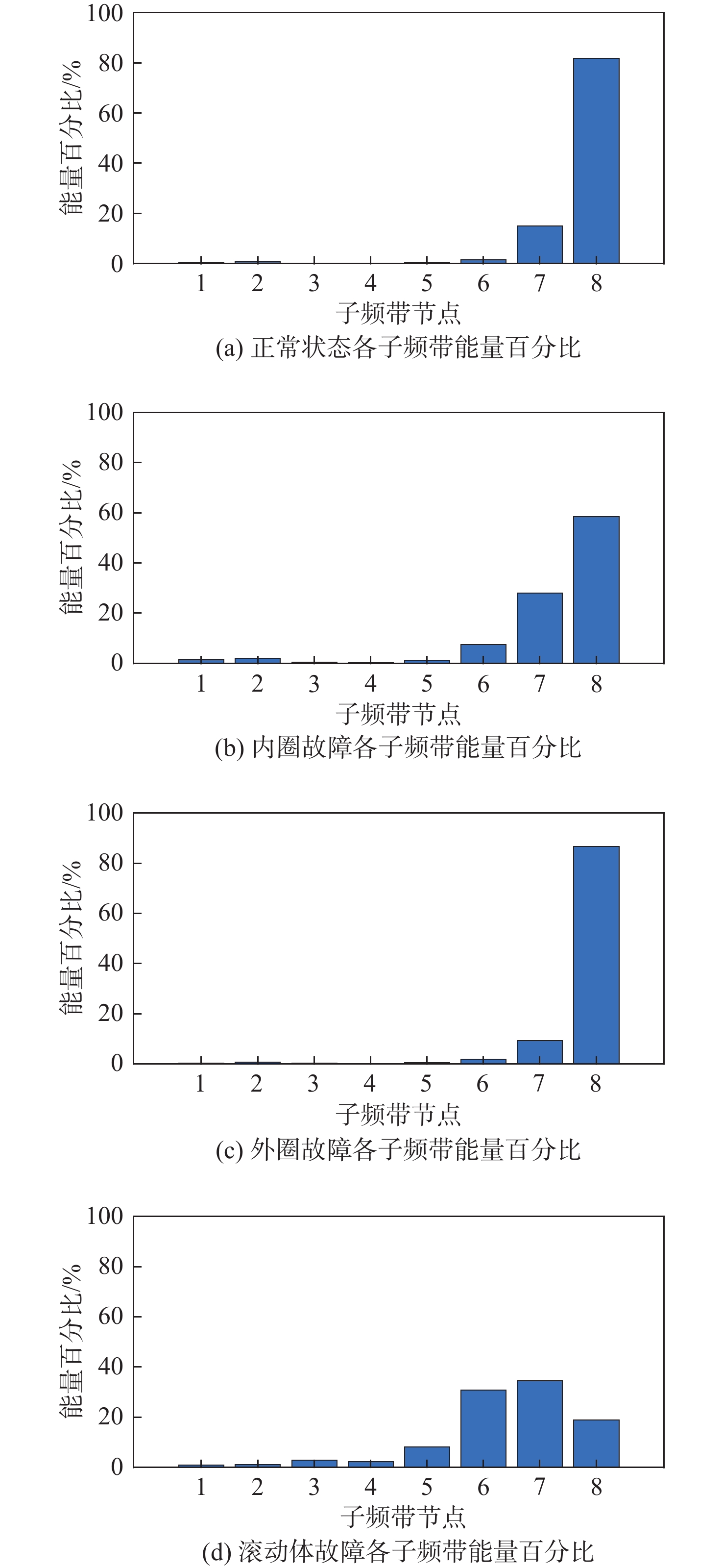
进一步地，对各运行状态的振动信号进行三层小波包分解，获取不同运行状态的子频带能量值，其百分比如图4所示。由于在不同状态下，子频带的能量占比均超过80%，分别选择能量百分比排名前三的子频带能量值，作为时频域高敏感特征参数。

图  4  不同运行状态下信号子频带能量百分比

Figure  4.  The energy percentage of signal sub bands under different operating states

下载: 全尺寸图片 幻灯片

从图4可以看出，不同运行状态下子频带节点6～节点8的能量百分比均高于其余节点的能量百分比，因此选择E₆～E₈为时频域高敏感时频特征参数。

根据以上对时域、频域、时频域特征参数的分析，最终构建多域特征参数集{T₁,F₃,E₆,E₇,E₈}。

2.   改进ELM网络模型

2.1   ELM网络模型

ELM作为一种新型SLFN，与传统神经网络方法不一样，先随机生成输入层权值和隐含层神经元阈值，再使用最小二乘估计对SLFN进行训练^[15]。这样可以避免梯度下降法可能带来的训练不稳定问题。相比传统的监督式学习，ELM不仅学习速度快，而且有较好的鲁棒性。

设ELM的输入矩阵为[X_i, E_i]，其中，X_i=[X_i1, X_i2, … , X_iN]^T ∈ R^N，E_i=[E_i1,E_i2, …, E_iM]^T ∈ R^M，X_i为N维输入样本，E_i为M维输出期望。原始ELM模型可表示为

式中：β_j为隐含层输出权值；f(·)为激活函数；H为隐含层数；W_j为随机产生的输入层权值；b_j为输入层阈值；Y_i为实际输出。

将式（13）简化为矩阵形式：

式中：V为隐含层输出矩阵；β为权值矩阵。

当给定W_j和b_j保持不变时，则可将式（14）转变成权值矩阵β最小二乘解：

式中，V⁺为V的Moore-Penrose广义逆^[16]。

由此可见，ELM在训练效率和参数调整方面具有优势，不过也存在一些问题，尤其是ELM的初始权值参数多为随机定义，在训练过程中可能会出现部分参数值为零的情况，导致部分隐藏节点被屏蔽，从而影响了最终的识别精度。为了解决这一问题，将SSA与ELM相结合，可以对ELM的隐含层输出权值β_j和输入层阈值b_j进行优化改进，从而提高ELM的识别精度和性能。

2.2   麻雀搜索算法

SSA算法模拟了麻雀群体觅食及反捕行为，这种群体协作的思想使得SSA成为一种新型的智能优化算法^[16]。在SSA中，发现者负责寻找食物资源，并指导整个种群觅食的方向；追捕者根据发现者找到的食物位置，进行移动追捕，同时预警机制保证种群安全。基于此，构建SSA数学模型，发现者麻雀的位置更新方法为

式中：$S_{ij}^t$是第t次迭代时第i只麻雀在第j维的位置信息；t_max为最大迭代次数；Q为随机数且服从正态分布；L为单位矩阵；a为随机数且a∈(0,1]；A为警惕阈值；Z为安全阈值。

其次，追捕者麻雀的位置更新方法为

式中：S ^t_w为第t次迭代时所有麻雀的最差位置；N为麻雀种群个数；S^t_p为第t次迭代时追捕者的最优位置；K_p=K^T(K K^T)⁻¹，K为随机赋值1或−1的多维矩阵。当i >n/2时，表明第i个追捕者适应度较低，没有从当前发现者的位置获得充足的食物。

最后，当麻雀种群感知到危险时，其位置更新方法为

式中：$S_{\text{b}}^t$为第t次迭代时所有麻雀的最优位置；γ 为步长调节因子；ξ为随机数；f_i为第i只麻雀的适应度值；f_b为全局最优适应度值；f_w为全局最差适应度值；ε为极小常数且大于0。

2.3   改进ELM故障诊断模型

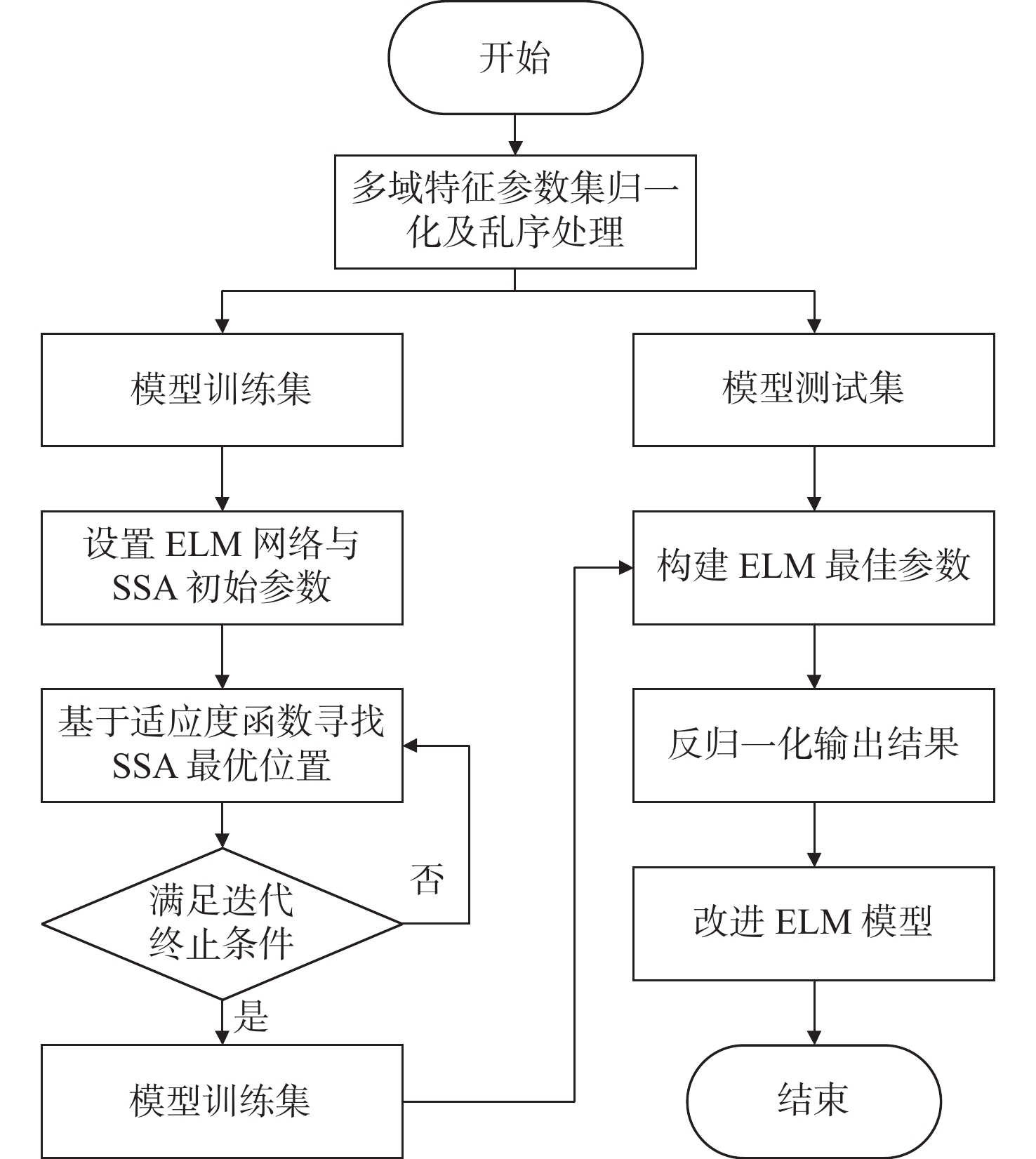
当ELM的输出矩阵为非满秩状态时，由于其隐含层权值及阈值的设置是随机定义的，其网络的泛化性将受到一定的波动。通过SSA算法对ELM参数进行调优分析，可构建泛化性能更好的故障诊断模型。基于此，改进ELM故障诊断模型流程如图5所示。

图  5  改进ELM模型流程图

Figure  5.  Improvement of the ELM model flow diagram

下载: 全尺寸图片 幻灯片

1）构建多域特征参数数据集，对训练集和测试集进行划分并归一化数据；

2）对SSA算法的种群数量进行初始化，赋予ELM参数并设置迭代条件；

3）设置适应度函数并完成种群角色划分，计算适应度函数，从而选择当前最差和最好个体位置；

4）更新发现者、追捕者以及预警个体位置，计算并保存相关状态参数；

5）对比最优位置与当前迭代位置参数，更新最优位置；

6）是否满足迭代终止条件，若不满足则返回步骤4）；

7）将最优参数赋予ELM并构建当前最优ELM网络结构模型。

3.   实验验证

3.1   电机试验台架的实验数据验证

为了验证所提方法的有效性，采用船舶用电机试验台架的实验数据，基于改进ELM模型进行电机轴承状态识别。

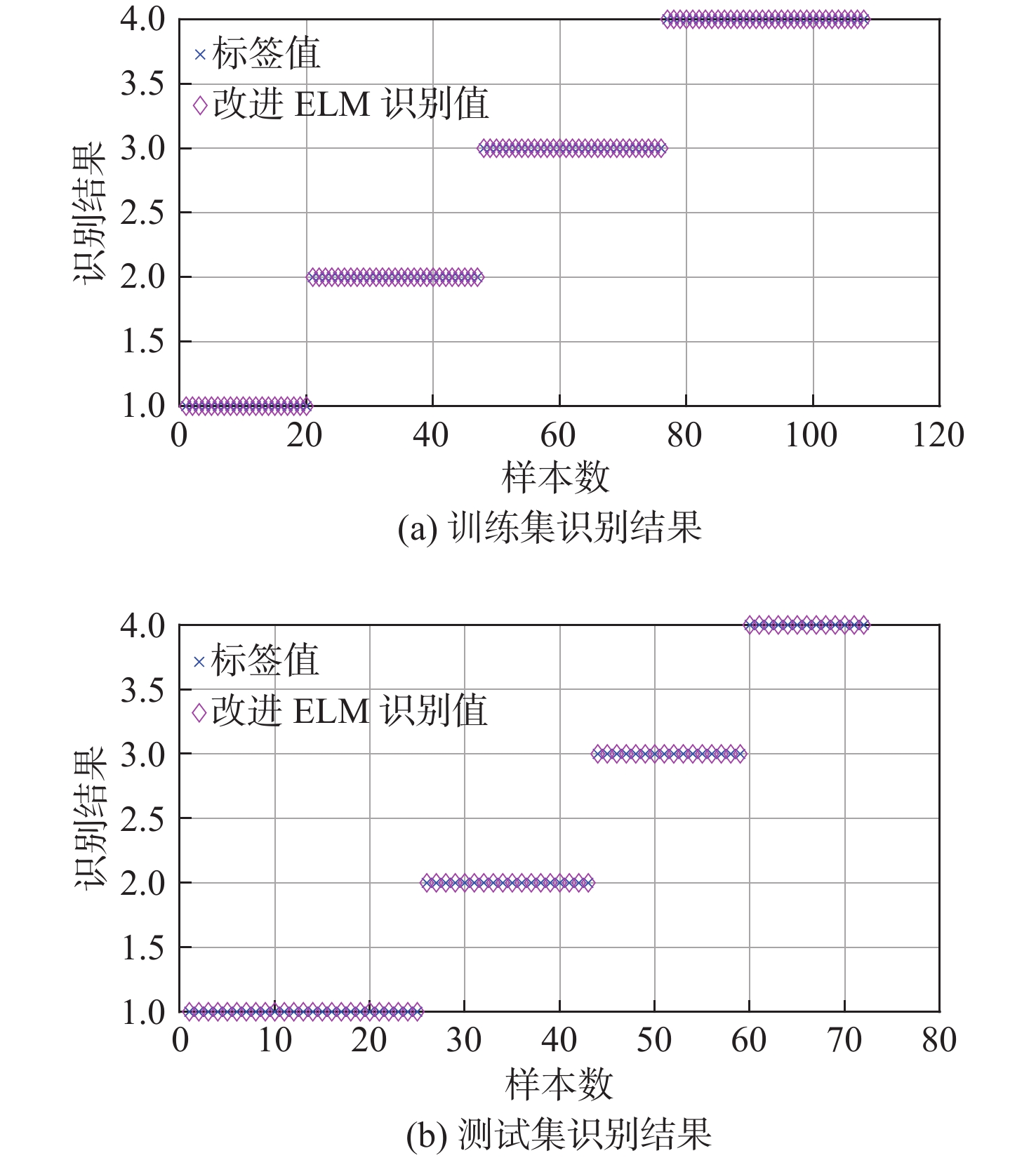
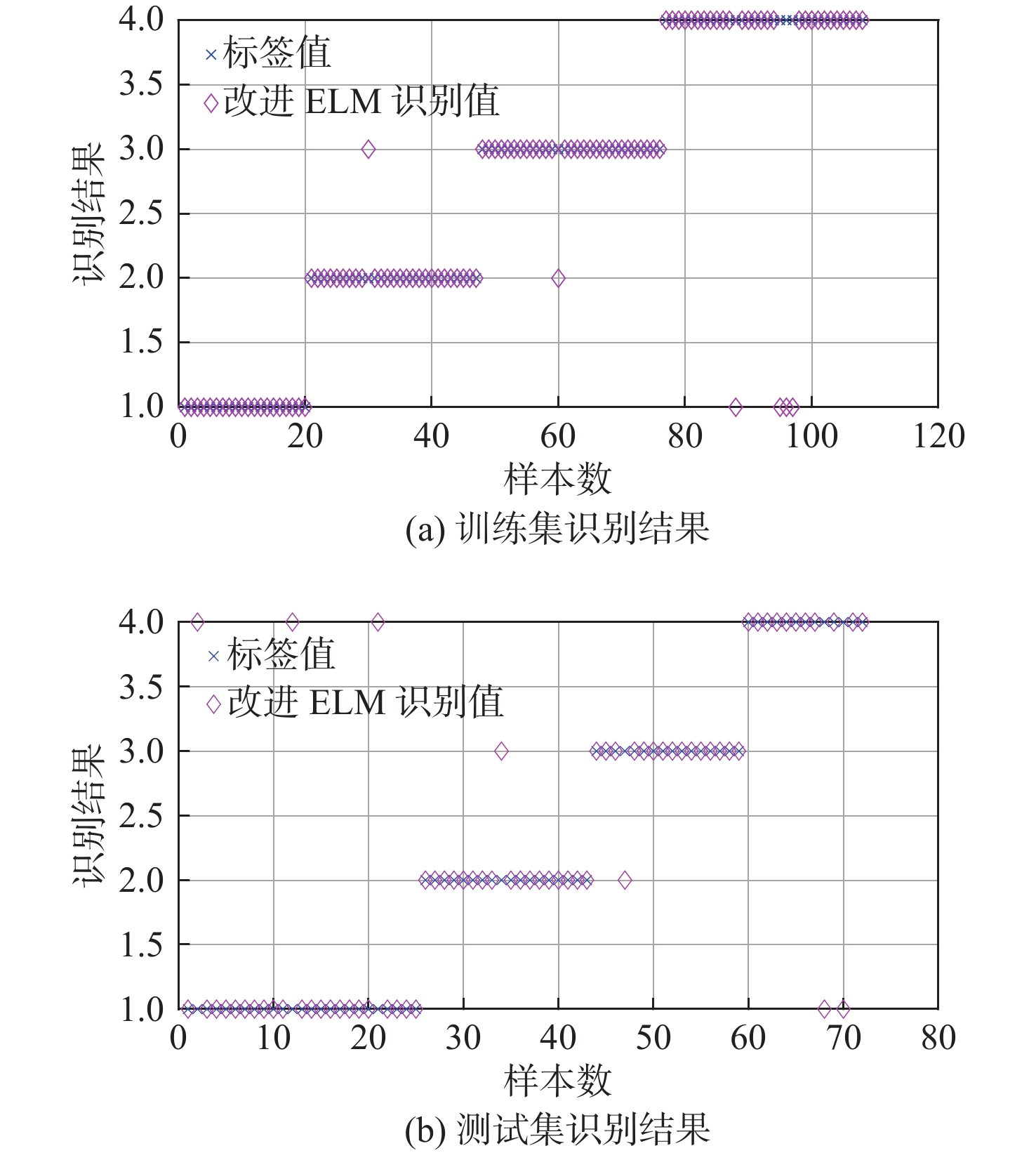
由1.4节可知，通过对数据集时域、频域、时频域特征参数的分析，最终构建多域特征参数集{T₁, F₃, E₆, E₇, E₈}，并将其输入改进ELM模型中。在本实验中，设置改进ELM模型的隐含层神经元数量为20，迭代次数为20，同时采用了麻雀种群优化算法，其中麻雀种群数量为10，发现者数量为3，追捕者数量为7。实验过程中，记录每次迭代的损失值和准确率，并检查模型的收敛性。实验结果显示，随着迭代次数增加，损失值逐渐降低，准确率逐步提高。在第17次迭代时，模型的损失值达到0.01，表明已接近收敛。识别结果如图6所示。

图  6  基于改进ELM故障诊断模型的识别结果

Figure  6.  Identification results based on improved ELM fault diagnosis model

下载: 全尺寸图片 幻灯片

从图6可以看出，模型在训练集和测试集上的识别精度均为100%，说明本文所提方法能够有效识别电机轴承状态。

进一步地，为了验证多域特征参数集的优越性，移除时频域高敏感特征参数，仅基于时域和频域的高敏感特征参数构建模型的输入参数集，识别结果如图7所示。

图  7  基于时域与频域高敏感特征参数的识别结果

Figure  7.  Recognition results based on high sensitivity symptom parameters in time and frequency domains

下载: 全尺寸图片 幻灯片

从图7的识别结果可以看出，移除时频域特征参数集后，训练集和测试集的识别精度分别为94.4%和90.3%，与多域特征参数集基于改进ELM的识别结果相比，分别下降了5.6%与9.7%，表明多域特征参数集可以提高改进ELM故障诊断模型的识别精度。

3.2   开源实验数据验证

为了进一步验证所提方法的广泛适用性，采用美国凯斯西储大学（CWRU）的电机轴承开源实验数据^[17]，对模型进行验证，并与其他方法进行对比。选择电机驱动端的轴承振动信号，采样频率为12 kHz，转速为1 797 r/min，电机负载为0 HP，电机运行状态分别为正常状态、轴承内圈故障、轴承外圈故障、滚动体故障。

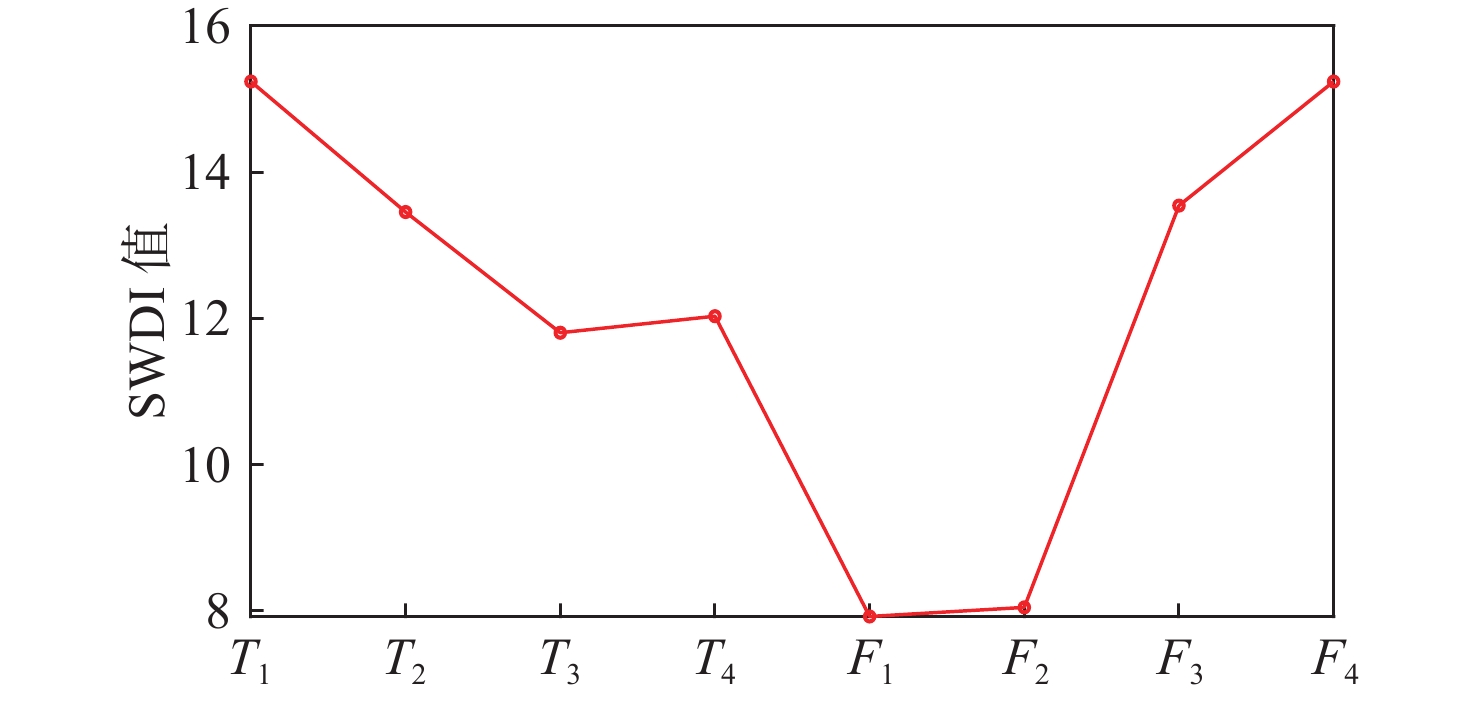
首先，将各运行状态的振动信号数据以每段4 096个数据点划分，每段信号共可分为45组，计算各信号的时域特征参数与频域特征参数，并计算各特征参数的SWDI值，结果如图8所示。

图  8  CWRU数据各特征参数的SWDI值

Figure  8.  SWDI values of various symptom parameters in CWRU data

下载: 全尺寸图片 幻灯片

从图8可知，与其他特征参数相比，时域特征参数T₁与频域特征参数F₄的SWDI值最为突出，因此选择T₁为时域高敏感特征参数，F₄为频域高敏感特征参数。

进一步地，对不同运行状态下的振动信号进行三层小波包分解，获取不同运行状态的子频带能量百分比。最后计算结果显示，不同运行状态下的子频带节点4～节点6的能量百分比均高于其余节点的能量百分比，因此选择E₄～E₆为时频域高敏感特征参数，构建多域特征参数集{T₁, F₄, E₄, E₅, E₆}，并进行归一化及乱序处理。

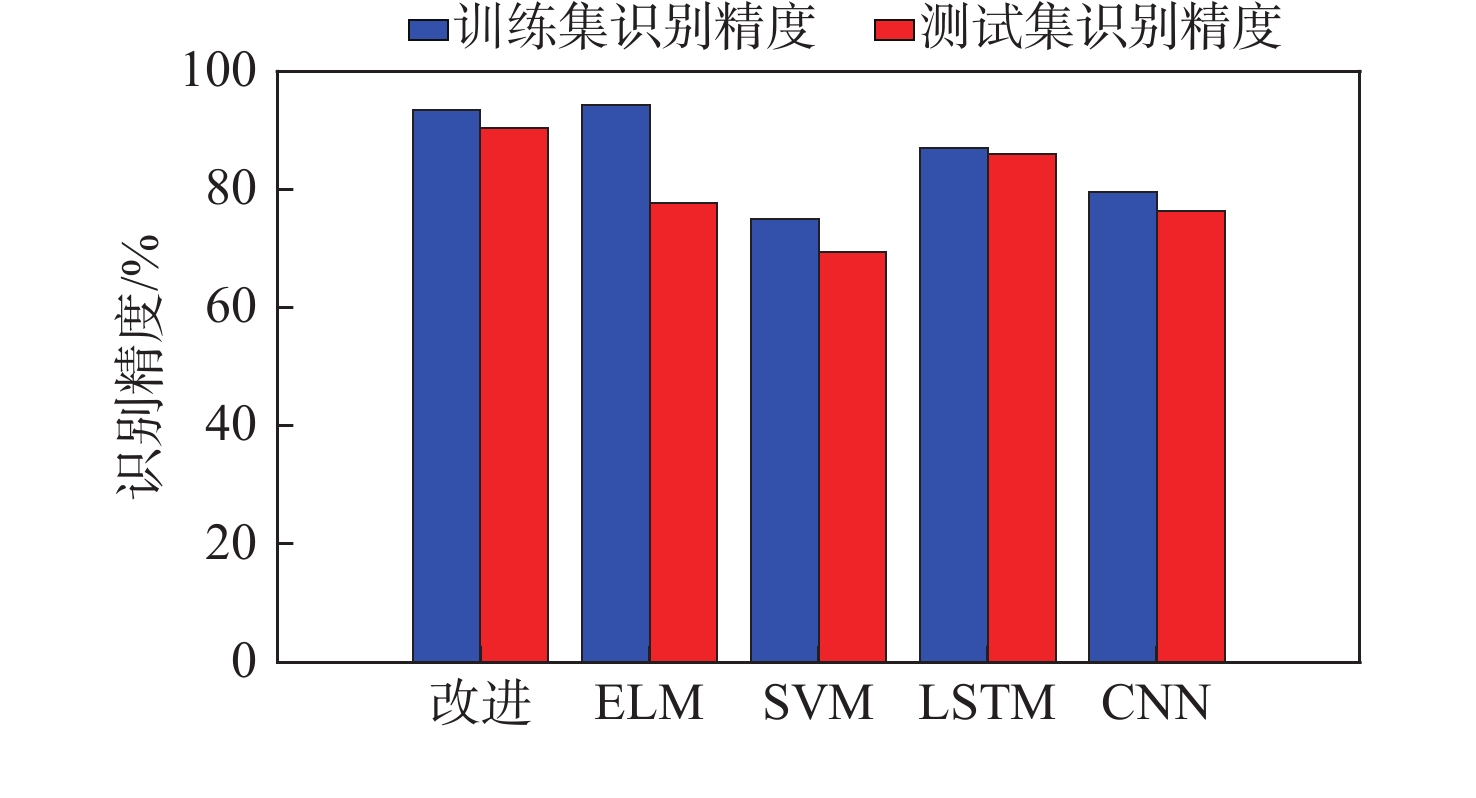
为了将更多数据用于训练且更准确地进行模型评估，将60%的多域特征参数集设为训练集，40%设为测试集，将其分别输入改进ELM模型、原始ELM模型、SVM模型^[18]、LSTM模型^[19]和CNN模型^[20]中。为确保参数设置的有效性，进行了系统的参数调优。评估不同隐含层神经数量、惩罚因子和学习率等参数对模型性能的影响。经过多轮实验，发现当前设置的参数在多个性能指标上优于其他组合。其中，设置改进ELM模型和原始ELM模型的隐含层神经数量均为20，迭代次数为20，并设置改进ELM模型中的麻雀种群数量为10，其中发现者数量为3，追捕者数量为7；设置SVM模型的惩罚因子为4，采用线性核函数；设置LSTM模型和CNN模型的初始学习率为0.3，学习率下降因子为0.1，均采用Adam 梯度下降算法，最大训练次数为300。基于此，各模型诊断结果的识别精度如图9所示。

图  9  各模型识别精度对比图

Figure  9.  Comparison chart of recognition accuracy of various models

下载: 全尺寸图片 幻灯片

从图9可知，改进ELM模型的训练集识别精度达到93.6%，与原始ELM模型的训练集识别精度基本一致，但是改进ELM模型的测试集识别精度为90.5%，相较于原始ELM模型提高了12.7%；SVM模型和CNN模型的训练集和测试集识别精度均低于80%，LSTM模型训练集和测试集识别精度分别为87.0%与86.1%，识别效果均不如改进ELM模型。

进一步地，为了比较各模型识别能力的稳定性，对各模型分别进行10次运算，计算各自测试集识别精度的均值与方差，结果如表2所示。

表  2  各模型诊断结果的指标对比

Table  2.  Comparison of diagnostic indicators among different models

指标	不同诊断模型
	改进ELM	ELM	SVM	LSTM	CNN
均值	0.928	0.819	0.754	0.858	0.731
方差	0.001 6	0.005 7	0.005 2	0.020 9	0.001 6

下载: 导出CSV 

| 显示表格

从表2可知，改进ELM模型在识别精度均值和方差上的表现均为最优，说明该模型不仅具有较强识别能力，而且识别精度高，具有良好的稳定性；对应地，其他模型的识别精度均值和方差表现均不如改进ELM模型，其中LSTM模型的识别精度均值虽然达到了0.858，但是其方差为0.020 9，高于其他4种模型，说明该模型的稳定性较差。

4.   结　论

本文提出了一种基于多域信息融合与改进ELM的船舶电机轴承故障诊断方法，又基于船舶电机轴承振动信号在时域、频域与时频域内的特征信息，经验证，该模型通过多角度提取故障特征，提高了特征提取的适应能力；同时，提出基于SSA的改进ELM模型，并证明了该模型故障识别精度较高，且具有良好的稳定性。

但是，本研究所用实验数据与船舶真实运行环境下电机故障实验数据还存在一定差异，后续有待于进一步验证所提方法的适应性和有效性。同时，对于小样本故障状态的识别能力也有待于深入研究。