Modeling and characteristic analysis of unsteady broadband excitation spectrum of thruster based on OU-Gaussian process
-
摘要:目的
为解决舰艇声振预报和调控中推进器激励信息获取的难题，提出一种基于奥恩斯坦−乌伦贝克（Ornstein-Uhlenbeck，OU）−高斯过程的湍流诱导推进器非定常宽带激励广义表征模型。
方法利用OU随机过程理论和叶元体理论，推导泵喷转子宽带激励功率谱的近似解析模型。通过Sobol全局灵敏度分析获得模型参数的作用频段及其影响规律，并经计算流体力学（CFD）计算结果验证模型合理性和泛用性。
结果结果表明，该模型能准确捕捉非定常激励功率谱中的宽带衰减特性与驼峰特征，参数具有很强的频率依赖性，其中，表征OU过程的部分参数作用频段较宽，而决定高斯函数的各参数集中作用于驼峰附近频段。在泵喷推进器推力功率谱描述上，广义表征模型与CFD结果表现出一致性，且从统计学置信区间角度得到验证。
结论此模型为显式参数模型，计算精度高、速度快，可为舰艇声振调控提供简洁可靠的经验谱输入条件，还可为推进器非定常激励的反演识别提供先验信息约束，减轻反问题的病态性并提高识别精度。
-
关键词:
- 奥恩斯坦−乌伦贝克（OU）−高斯广义表征模型 /
- 推进器非定常激励 /
- 宽带功率谱 /
- 模型参数 /
- 全局灵敏度分析
Abstract:ObjectivesTo solve the problem of obtaining propeller excitation information in the prediction and control of ship acoustic vibration, a generalized characterization model of the unsteady broadband excitation of a propeller induced by turbulence based on the Ornstein-Uhlenbeck (OU)- Gaussian process is proposed.
MethodBy using the OU stochastic process theory and blade element theory, an approximate analytical model of the broadband excitation power spectrum of a pump-jet rotor is derived. The operating frequency ranges and influence patterns of the model parameters are obtained through Sobol global sensitivity analysis, and the rationality and generality of the model are verified by the computational fluid dynamics (CFD) calculation results.
ResultsThe results show that the model can accurately capture the broadband attenuation characteristics and hump features in the non-stationary excitation power spectrum. The parameters have strong frequency dependence. Among them, some parameters characterizing the OU process operate in a wide frequency range, while parameters determining the Gaussian function are focused on the frequency band near the hump. In the description of the thrust power spectrum of the pump-jet propeller, the generalized characterization model is consistent with the CFD results, and is verified from the perspective of the statistical confidence interval.
ConclusionThe proposed explicit parametric model has high computational accuracy and speed. It can provide a simple and reliable empirical spectral input condition for the acoustic vibration control of naval vessels. It can also provide prior information constraints for the inversion and identification of the non-stationary excitation of the propeller, mitigating the ill-posedness of inverse problems and improving the identification accuracy.
-
0. 引 言
推进器激励是潜艇艉部辐射噪声的主要激励源之一，湍流诱导的非定常激励经轴系耦合放大作用引发艇体艉部振动，并在整艇低频辐射噪声谱中形成声纹特征[1]。因此，准确掌握推进器非定常激励特性，为舰艇声振预报和调控提供可靠的输入条件，具有重要工程价值。
直接测量法和理论预测法是目前获取非定常激励的两种主要手段。直接测量法将动力仪嵌入推进器与转轴的连接面，在激励源附近直接获取传递力信息，能够更好地捕捉复杂海洋环境下推进器激励的动态行为，具备高测量精度与获取速度[2]。然而，集成动力仪可能会改变推进轴系的动力学特性，进而引发潜在的系统可靠性问题。理论预测法中的条带法[3-4]具有计算效率高、物理概念清晰的优势，然而其求解需准确的桨叶翼型参数和螺旋桨所处的流场参数，因此在实际航行环境往往难以应用。随计算机技术的发展，计算流体力学（computational fluid dynamics, CFD）凭借其高精度和对复杂几何形状的强大适应性，逐步成为理论预测法的主流，并被广泛应用于各类流场、推进器的非定常激励力模拟中[5]。但其预测精度严重依赖于网格质量与对流场的先验估计，难以准确预测非试验环境下的真实激励力。此外，CFD极高的算力需求与过长的计算时间也难以满足声辐射预报等任务对实时性的需求。为克服直接测量和理论预测方法在实用性和实时性上的不足，基于易获取的轴系动力学响应和先验的系统模型，反演推进器激励力，是近年来被广泛关注的可行方案，并已发展出众多时域与频域反演方法[6-7]。推进力反演方法的核心是结合真实结构的时频域传递模型，将系统输入在模型响应子空间上的投影（即时频域响应）进行逆映射，获得输入的近似值。反问题由于内置矩阵求逆过程，在大条件数模型矩阵的制约下，其解往往是病态的，即测量与模型的误差会放大反映在输入的预测中[8]。针对此问题，学者们主要聚焦于估计并降低噪声影响，提出如正则化[9]、滤波[10]和贝叶斯推断[11]等方法，并取得一定效果。然而，上述方法尚未充分利用对非定常推力功率谱特征的先验认知，因此当无法获得准确误差估计或系统能观性不足时仍存在解的发散和不合理估计问题[12]。
对推进器非定常宽带功率谱的近似解析解研究可以追溯到1974年，Sevik[13]从10叶螺旋桨的水筒试验中观察到推力功率谱的宽带衰减特性及驼峰现象，并尝试提出相关性法进行预报。由于忽略了螺旋桨旋转的影响，该预报手段未能有效捕捉叶频处的驼峰。该方法随后由Martinez[14]优化。Blake[15]使用谱方法计算非定常宽带力，总力谱即为湍流波数谱和力响应函数在展向上的积分，随后Kirschner等[16]提出条带理论完善该方法的数值解，但该预报结果受限于事先设定的湍流积分尺度，无法同时精确预报驼峰和宽带特征。上述研究旨在基于各类湍流理论，结合流场特征的先验估计，正向预测激励力。尽管这类方法提供了非定常激励的解析模型，但模型的准确性依赖于对参数的正确评估，且高维积分的求解只能借助有限离散方法实现（这也推动了CFD的发展）。相反，在进行反问题求解时，更期望一种简单有效的解析模型作为约束，从而降低解的复杂度。同时，采用系统响应来预测模型参数，也可从根本上避免流场估计不足的影响。
受桥梁[17]、风力机[18]和机翼[19]等风载解析模型中对非高斯脉动力近似过程的启发，本文将使用奥恩斯坦−乌伦贝克（Ornstein-Uhlenbeck，OU）随机过程理论描述湍流中粒子的布朗运动，以捕捉谱线的宽带衰减特征，使用高斯函数模拟叶频驼峰，提出一种表征湍流诱导水下推进器宽带功率谱的OU−高斯经验模型。进而分析各模型参数的作用频段及其影响程度，并基于泵喷推进器在不同转速下的CFD功率谱结果，从统计学置信区间的角度验证经验模型的合理性，并分析转子转速变化对模型参数的影响规律。
1. OU−高斯广义表征模型建立
对非定常激励组成成分及各成分诱因的准确认知是建立表征模型的基础。推进器（泵喷/螺旋桨）非定常激励谱由低频线谱和宽带随机谱构成[13,20]，在宽带整体呈现衰减特征，伴随着叶频线谱附近的驼峰出现。由于入流的空间非均匀性，当螺旋桨转动一个相邻桨叶的夹角时，同一空间位置的伴流场将以叶频重复作用于下一个桨叶，产生低频线谱；而时间非定常性又使得相同位置的流场对前后两个桨叶的作用效果不尽相同，进而在线谱附近产生非周期分量，也就是叶频驼峰；此外，在非叶频附近，非定常的湍流在宽频范围内随机激励桨叶，形成具有湍流特征的宽带力；后两者构成激励的宽带随机谱。从上述研究可知，激励宽带谱中的非驼峰成分由湍流主导，而驼峰则通过湍流与叶频复合作用产生。
微粒在流场中与周围分子相互作用产生无规则的运动速度变化，即为熟知的布朗运动。在湍流中，相邻流层界面被破坏，各流层间出现滑动混合现象，流体分子相互作用增强，引起更显著的速度脉动及更分散的流速区间。研究显示[21]，作用于微粒上的力由两部分构成：一是由斯托克斯定律揭示的正比于微粒运动速度的黏滞力；二是由于流体分子碰撞产生的随机力。因此，有关微粒的一维布朗运动方程可用Langevin方程[22]来描述
m¨x=−λ˙x+F (1) 式中：m为水分子质量；x为水分子脉动位移；λ表示流体黏滞系数；分子碰撞力F=fη（t）为高斯随机过程，f为由玻尔兹曼能量和流体黏滞系数决定的随机力幅值，η（t）为单位高斯白噪声。
若以水分子的脉动速度v代替脉动位移x，则式（1）可改写为
˙v=−λmv+fmη (2) 上式即为具有惯性的自由粒子布朗运动的OU理论[21]，粒子脉动速度v服从OU随机过程。
求解式（2）所示的微分方程，速度的时间序列为
v(t)=v(0)e−λmt+fm∫t0e−λm(t−s)dWs (3) 式中：v(0）为0时刻速度初值；dWs=η(s)ds为微分随机游走过程，其本质是单位高斯白噪声η（s）在微小时间ds上的作用总和。式（3）可分解为两项：其一是由初始脉动速度v（0）诱导的确定性速度，该速度由于流体黏滞力随时间衰减至0；其二是由流场随机力η(t）诱导的随机性速度，该速度不具备衰减性，表示湍流中水分子的脉动速度将会一直存在。
定义θ=λ/m和σ =f/m分别为OU过程的漂移系数和扩散系数，则式（3）可简化为
v(t)=v(0)e−θt+σ∫t0e−θ(t−s)dWs (4) 由于式（4）所示的解存在随机游走项Ws，因此单个水分子的运动行为难以在时域上精确描述。此外，湍流的本质为大量脉动速度各异的水分子集合，因此，从随机理论出发获取流场的频域统计量（即力谱和功率谱），可消除随机成分的影响，得到更具工程指导意义的稳健结果。V（t）的均值和协方差为
E[v(t)]=v(0)e−θt+E[σ∫t0e−θ(t−s)dWs]=v(0)e−θt (5) Cov[v(t),v(s)]=σ22θ(e−θ|t−s|−e−θ(t+s)) (6) 其中式（6）中协方差的推导运用了伊藤等距公式
E[∫t0X(u)dWu∫s0Y(v)dWv]=∫0min (7) 从式（5）和式（6）可知，当流场经长时间（t→∞）演变到达稳态时，负指数项随时间t衰减至0，OU过程的前2阶矩（均值、方差）均会收敛到某个值附近，被称为渐进均值和渐进方差。而由于入流湍流固有的平稳性假设，可用渐进均值和渐进方差代替均值和方差
{\text{E}}\left[ {v\left( t \right)} \right] = 0, {\text{Cov}}\left[ {v\left( t \right),\;\;v\left( s \right)} \right] = \frac{{{\sigma ^2}}}{{2\theta }}{{\text{e}}^{ - \theta \left| {t - s} \right|}} (8) 进而可基于自相关函数的傅里叶变换计算脉动速度的功率谱，分别为：
{R_v}\left( \tau \right) = {\text{E}}\left[ {v\left( t \right)v\left( {t + \tau } \right)} \right] = \int_{ - \infty }^\infty {v\left( t \right)v\left( {t + \tau } \right){\text{d}}t} = \frac{{{\sigma ^2}}}{{2\theta }}{{\text{e}}^{ - \theta \tau }} (9) \begin{split} & \;\;{S_v}\left( \omega \right) = 2\int_0^\infty {{R_v}\left[ \tau \right]\cos \omega \tau {\text{d}}\tau } =\\& \frac{{{\sigma ^2}}}{\theta }{\text{Real}}\left\{ \int_0^\infty {{{\text{e}}^{ - \left( {\theta + {\text{j}}\omega } \right)\tau }}{\text{d}}\tau } \right\} = \frac{{{\sigma ^2}}}{{{\theta ^2} + {\omega ^2}}} \end{split} (10) 由于自相关函数的实偶性质，其傅里叶变换必为实数，式（10）中的Real{·}为取实部操作。
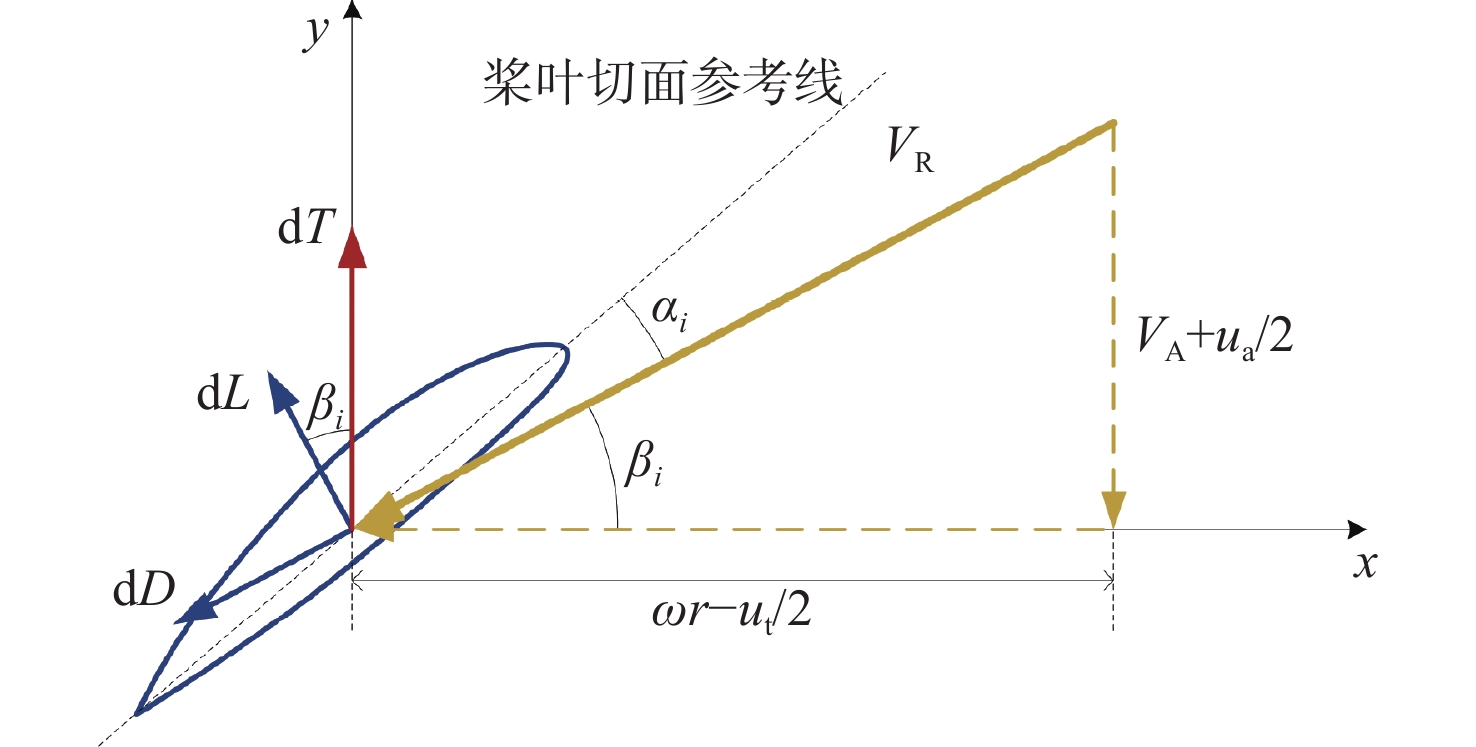
湍流水分子在桨叶上诱导的非定常推力可借助叶元体理论[23]进行评估，如图1所示，螺旋桨旋转时桨叶叶元体i承受流体的轴向推力为
{\text{d}}T = {\text{d}}L\cos {\beta _i} - {\text{d}}D\sin {\beta _i} (11) 式中：dD，dL和dT分别为叶元体受到的阻力、升力和轴向推力；αi和βi分别为来流攻角和水动力螺距角；VA，ua和ut分别为流场轴向进流速度、轴向诱导速度和周向诱导速度；ω和r分别表示螺旋桨转速和叶元体所处半径，各项速度在叶元体局部坐标系内组合成来流相对速度VR。其中，轴向/周向诱导速度前的1/2系数基于理想推进器理论下的伯努利原理获得，此处不予展开。
由儒可夫斯基升力公式得叶元体升力
{\text{d}}L = \rho {V_{\text{R}}}\left( r \right)\varGamma \left( r \right){\text{d}}r \propto \rho {V_{\text{R}}}^2\left( r \right){\text{d}}r (12) 式中：ρ为流体密度；Γ(r）为叶元体的速度环量，与入流速度成正比。定义叶元体阻升比ε = dD/dL后，式（11）可改写为
\begin{split} & \qquad\qquad{\text{d}}T = {\text{d}}L\cos {\beta _i}\left( {1 - \varepsilon \tan {\beta _i}} \right) \propto \\& \rho {V_{\text{R}}}^2\left( r \right)\cos {\beta _i}\left( {1 - \varepsilon \tan {\beta _i}} \right){\text{d}}r = C\left( r \right){V_{\text{R}}}^2\left( r \right){\text{d}}r \end{split} (13) 式中，系数C（r）受螺距角βi和阻升比ε影响，当假设叶元体螺距角随半径r变化较小且叶元体形状相似（ε不变）时，C（r）可视为定常系数。此时，叶元体推力dT与来流相对速度VR（r）的平方成正比，该结论与气动载荷规律[24]相符。考虑来流速度VR（r）由恒定速度成分V（r）和脉动速度成分v组成：VR（r）=V（r）+v。在湍流度较小（v \ll V ）时，忽略脉动速度的二次小量v2，则式（13）变为
{\text{d}}T = C\left( r \right)\left( {V{{\left( r \right)}^2} + 2V\left( r \right)v} \right){\text{d}}r (14) 式（14）展示了叶元体推力dT中除由恒定速度V产生的定常推力外，存在与脉动速度v正相关的脉动项，此脉动项也服从OU随机过程。进一步，对多个叶元体的脉动推力在半径方向积分获得螺旋桨的总推力
\begin{split} & \quad T = \int {{\text{d}}T} = \int {C\left( r \right)\left( {V{{\left( r \right)}^2} + 2V\left( r \right)v} \right){\text{d}}r} = \\& \int {C\left( r \right)V{{\left( r \right)}^2}{\text{d}}r} + 2\int {C\left( r \right)V\left( r \right)v{\text{d}}r} = {T_1} + {T_2} \end{split} (15) 式中，脉动速度v的积分项可看作多个OU过程的线性组合。而对于黏滞系数λ相同的同种流体（此时θ也相同），其满足式（2）OU过程的脉动速度v1和v2的线性组合v=k1v1+k2v2仍为OU过程
\begin{split} & \quad\qquad\qquad\qquad \dot v = {k_1}{{\dot v}_1} + {k_2}{{\dot v}_2} = \\& - \theta \left( {{k_1}{v_1} + {k_2}{v_2}} \right) + \left( {{k_1}{\sigma _1}{\eta _1} + {k_2}{\sigma _2}{\eta _2}} \right) = - \theta v + \eta \end{split} (16) 式中，η为两高斯过程η1和η2的线性组合，也为高斯过程。
因此，式（15）可分解为两项：一是由恒定速度激发的定常力T1；二是由湍流脉动速度激发的、服从OU过程的非定常力T2。非定常力T2的功率谱与式（10）相似
{S_{{T_2}}}\left( \omega \right) = \frac{{{\sigma ^2}}}{{{\theta ^2} + {\omega ^2}}} (17) 式中，θ和σ为非定常力T2广义上的漂移系数和扩散系数，后文不再与式（10）中相同形式的参数做区分。
此外，考虑到实际湍流流场的复杂性以及湍流模型的不完备性，螺旋桨真实推力可能还混有其他非定常成分T3，可假设为高斯白噪声，其功率谱恒定
{S_{{T_3}}}\left( \omega \right) = {c_{\text{w}}}^2 (18) 式中，cw为白噪声激励强度。
因此，在不考虑叶频驼峰时，螺旋桨非定常宽带功率谱为
{S_T}\left( \omega \right) = \frac{{{\sigma ^2}}}{{{\theta ^2} + {\omega ^2}}} + {c_{\text{w}}}^2 (19) 式（19）可明显看出OU过程随角频率ω的衰减特性。
大量研究表明[13-15,25]，非定常功率谱上的驼峰幅值关于中心频率（即叶频）对称，因此可采用高斯函数模拟，且与式（19）所示的OU模型乘性叠加，形成OU−高斯广义表征模型。不失一般性，后文使用频率f替换角频率ω，频率替换影响可通过调节待定参数抵消
{S_T}\left( f \right) = \left( {\frac{{{\sigma ^2}}}{{{\theta ^2} + {f^2}}} + {c_{\text{w}}}^2} \right) \times \prod\limits_{i = 1}^N {\left[ {{c_{{\text{g}},i}}\exp \left( { - \frac{{{{\left( {f - {f_{{\text{g}},i}}} \right)}^2}}}{{2{\sigma _{{\text{g}},i}}^2}}} \right) + 1} \right]} (20) 式中：θ和σ为决定OU过程的待定参数；cw为决定白噪声激励的待定参数；N为考虑的驼峰数；cg,i，fg,i和σg,i为对应第i阶驼峰的待定参数。
上述模型能表征宽带力功率谱两大特性，即宽带衰减特性和驼峰，并使用高斯白噪声考量模型误差。因此，只需式（20）改变待定参数，便可用于表述不同推进器或不同运行工况的变异性。
2. 模型参数影响规律
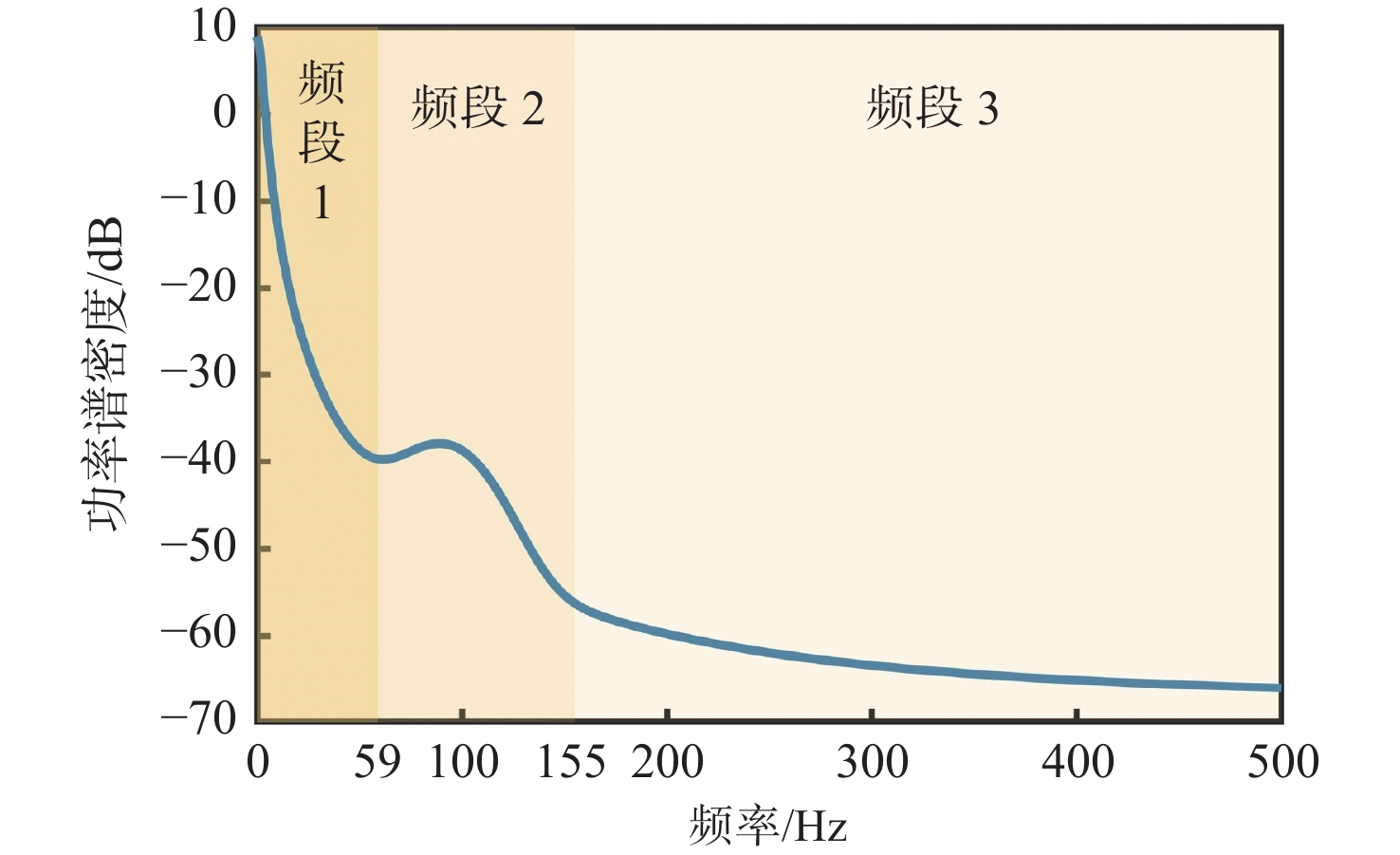
本节分析OU−高斯广义表征模型中各参数的作用频段及其影响规律。由式（20）表征的模型曲线示意图如图2所示（取N=1），各项模型参数设置为表1中的均值。从图2中可以看出，曲线清晰地捕捉到功率谱的宽频衰减特性以及驼峰。根据一阶驼峰的位置可将整条曲线划分为频段1（0～59 Hz）、频段2（59～155 Hz）和频段3（155～500 Hz）。
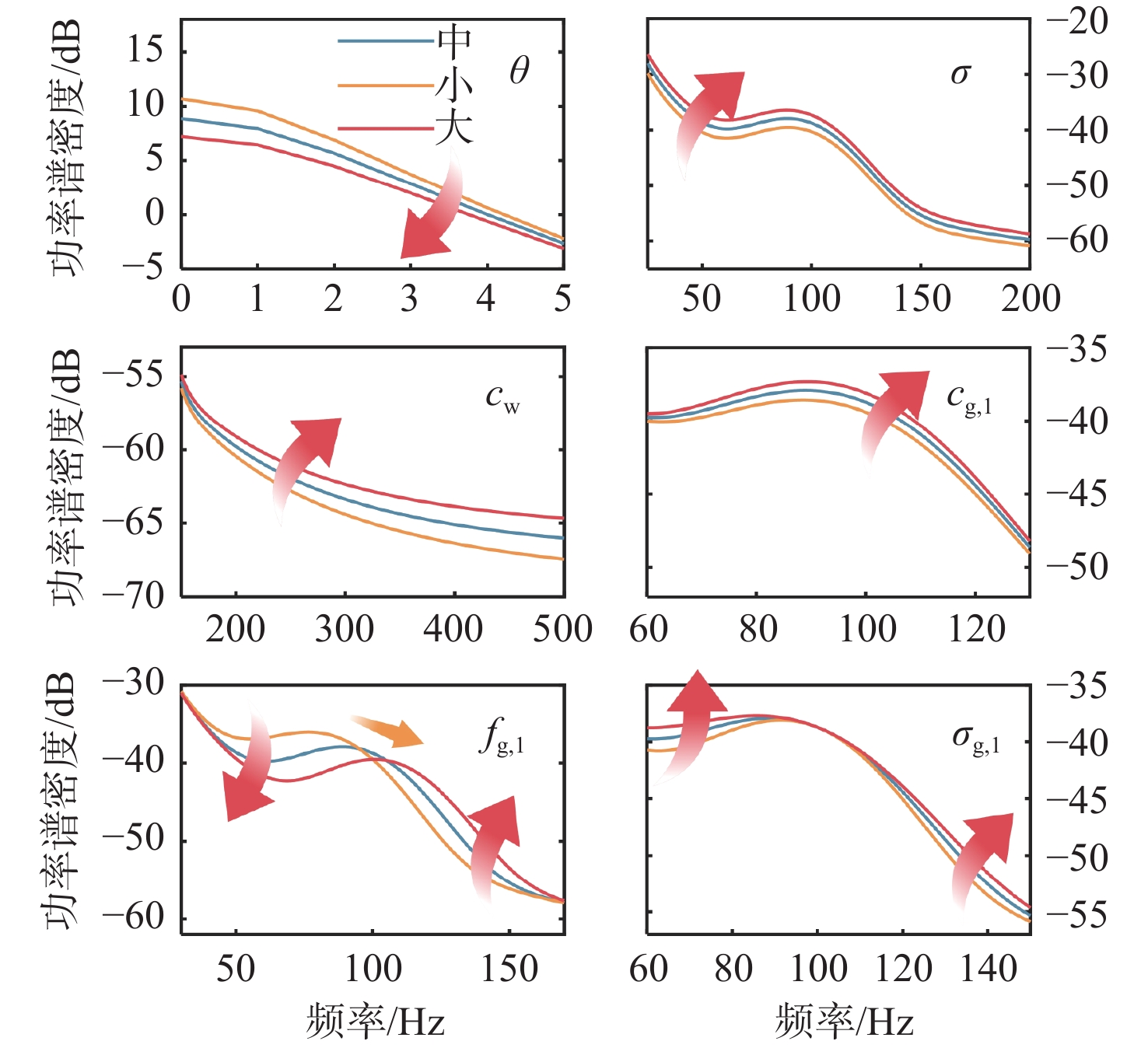
表 1 曲线示意图的参数值Table 1. Parameter values of the schematic diagram参数 均值 标准差（按10%均值） θ 3 0.3 σ 5 0.5 cw 0.02 0.002 cg,1 3 0.3 fg,1 100 10 σg,1 20 2 首先定性分析各参数对谱线的影响规律，按表1中的标准差分别取小、中、大3类参数值，基于控制变量的方式绘制曲线变化，如图3所示。其中，红色箭头代表功率谱曲线随参数增加的变化趋势。可以明显看出，模型对各参数具有很强的频率依赖性。在决定OU过程的3个参数中，漂移系数θ的控制范围集中在0～10 Hz的较低频段，且θ增大会抑制功率谱幅值；扩散系数σ影响范围接近整个频段，且功率谱幅值随σ增大而整体提高；白噪声强度cw的增加也具有正向增益，但其作用随频率升高才逐渐显著。决定高斯函数的3个参数则主要控制驼峰附近的频段2。其中，高斯中心频率fg,1通过改变驼峰位置从而使频段2功率谱出现不同的变化，具体表现为：增大fg,1，中心频率以下的频段的幅值降低，而高于中心频率的幅值升高，驼峰峰值往高频移动；高斯强度cg,1以及高斯标准差σg,1的增加均会提升驼峰幅值，但它们之间存在差异：cg,1主导中心频率附近的增益，σg,1则主导更远的频段。
![]()
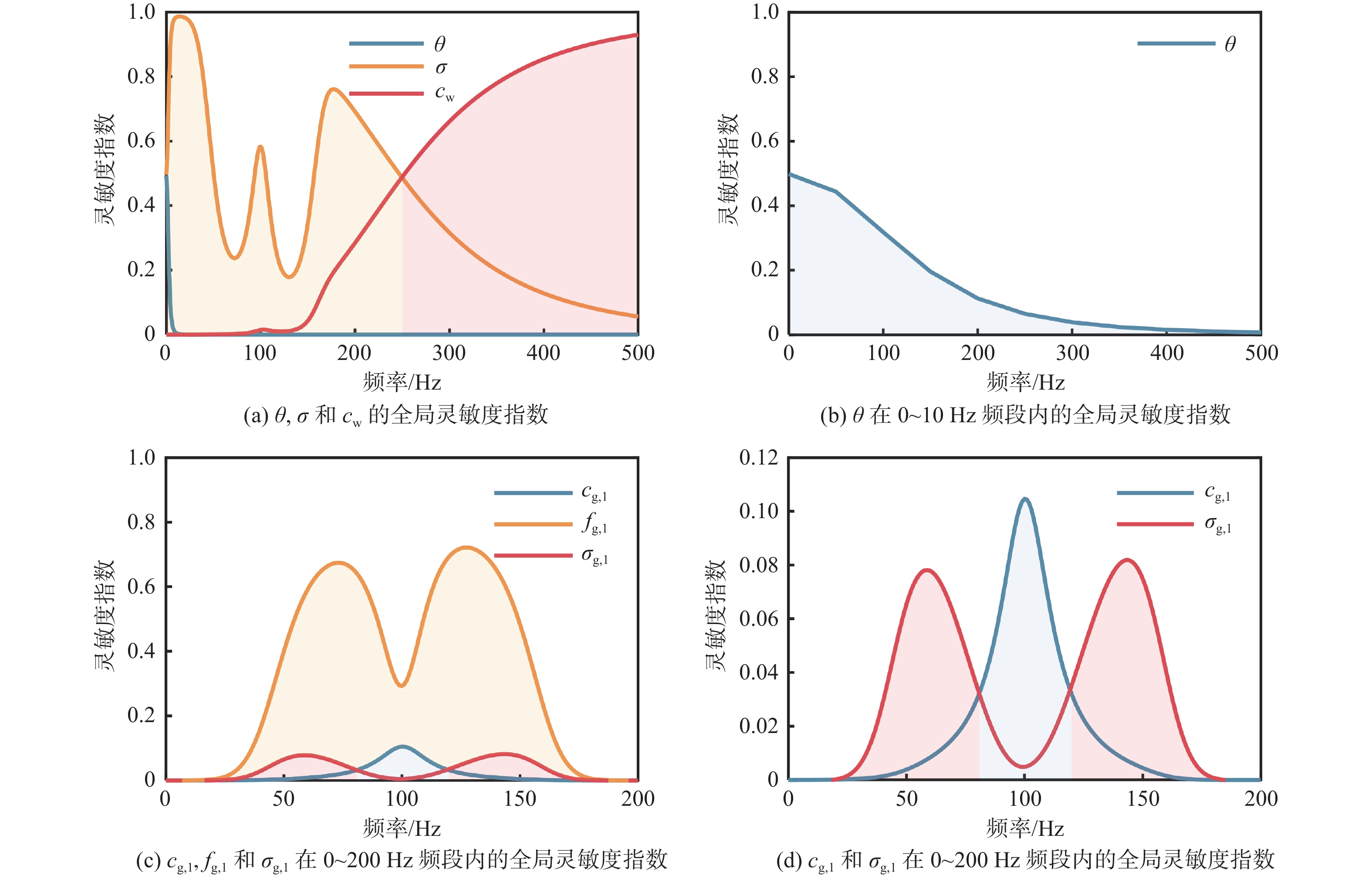
图 3 OU−高斯模型各参数（N=1）影响规律Figure 3. Influence law of each parameter in OU-Gaussian model (N=1)进一步定量分析不同参数对经验谱模型的全局灵敏度，即在0～500 Hz的频段范围内分析参数变化对曲线的影响程度大小。各参数服从表1所示的独立高斯分布（标准差按照10%均值大小处理）。经拉丁超立方采样后，采用式（21）所示的Sobol灵敏度函数[26]计算表征各参数独立变化的影响效果的一阶灵敏度指数。
\left\{ \begin{gathered} {D_i} = \frac{1}{M}\sum\nolimits_{j = 1}^M {g{{( A )}_j}( {g{{( {B_A^{( i )}} )}_j} - g{{( B )}_j}} )} \\ D = {\text{Var}}\left[ {g( A ),g( B )} \right] \\ {S_i} = \frac{{{D_i}}}{D} \\ \end{gathered} \right. (21) 式中：下标i=1,2,…,6分别指代模型的6个参数；Di为功率谱（分贝数）仅在第i个参数变化时的方差；待分析函数g(·)=20lgST( f )为式（20）功率谱的分贝表示；g(·)j为使用样本中的第j个采样点的函数值；A与B为两个样本数相等的参数样本集；BA（i）表示将样本集B中所有第i个参数的采样值替换为样本集A中同一参数的采样值；D=Var[g(A), g(B)]为功率谱（分贝数）在两个样本集的总方差；Si为第i个参数的Sobol灵敏度；采样样本数M为2×104。
图4所示为模型6个参数的全局灵敏度随频率的变化规律，与图3的定性分析一致，各参数的影响效果具有频率依赖性。其中，表征OU过程的3个参数θ，σ和cw的全局灵敏度指数如图4（a）所示。漂移系数θ的作用很小，且几乎只在0～10 Hz的较低频段内影响到曲线幅值（如图4（b）所示）。这是由于其受限于OU过程功率谱中分母（θ2+f 2）中频率平方项f 2的迅速增大，θ的作用被稀释。扩散系数σ在全频段均有影响，但其控制作用集中在0～250 Hz的频段1和频段2，且对频段1的影响显著。白噪声强度cw的效果则随频率的升高而逐渐增大，这是由于OU过程固有的宽带衰减特性变相放大了高频（频段3内）白噪声的贡献。决定高斯函数的3个参数cg,1，fg,1和σg,1的全局灵敏度指数如图4（c）所示，再次验证了定性分析结果，即三者主要作用频段均在驼峰所处的频段2（59～155 Hz）附近，对该区域之外的OU过程无明显贡献。其中，占主导作用的是高斯中心频率fg,1（如图4（c）所示），其直接定位高斯函数的位置，从而改变中心频率附近的驼峰幅值。高斯强度cg,1和高斯标准差σg,1的影响较小（如图4（d）所示），且作用范围不重叠。cg,1集中控制在中心频率周围的高斯函数，这是由于其与标准高斯函数乘性叠加，更高的高斯函数幅值（在中心频率附近）会更好地放大cg,1的作用；而σg,1控制远离中心频率的高斯函数段，其控制机理是在保持中心频率及峰值的情况下，改变驼峰宽度，因此，对距中心频率越远的函数幅值具有越强的控制效果。
![]()
图 4 OU−高斯过程各模型参数（N=1）的全局灵敏度指数Figure 4. Global sensitivity indexes of each parameter in OU-Gaussian process model (N=1)3. 模型验证
3.1 计算模型与宽带谱处理
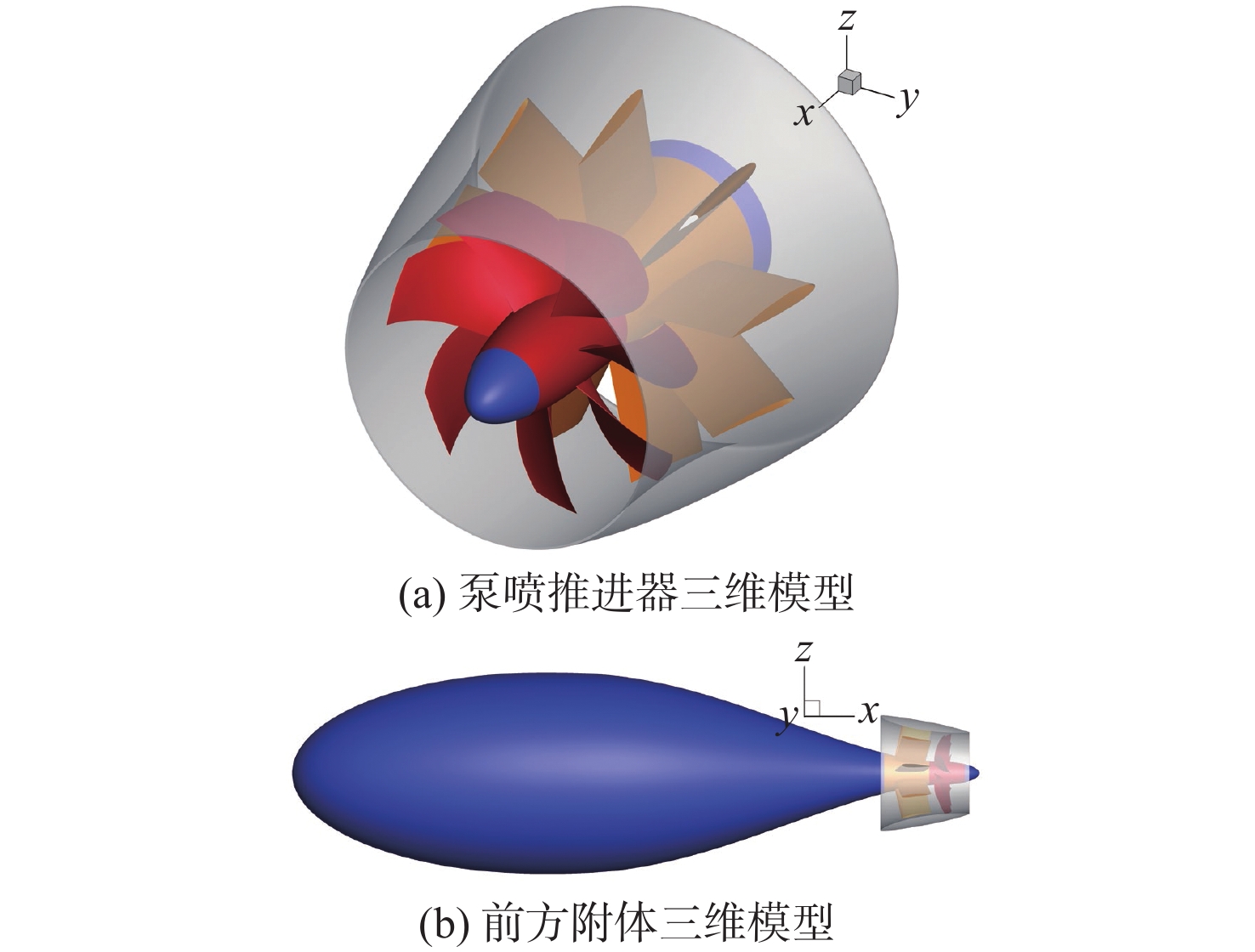
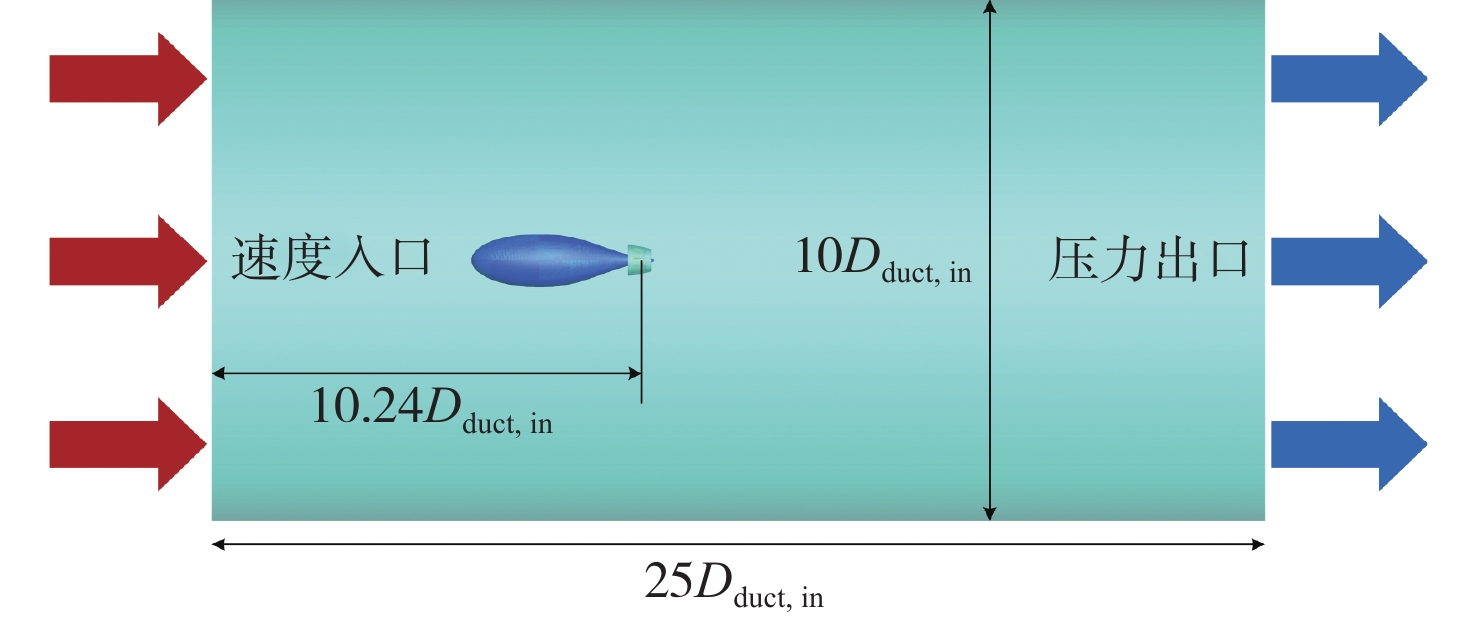
使用带附体的泵喷推进器模型来验证本文提出的OU−高斯广义表征模型的准确性。泵喷推进器采用前置定子的形式，由7叶转子和9叶定子构成，导管来自Groves等[27]为SUBOFF配备的RING-WING2环形罩，如图5所示。泵喷推进器是一种充分利用艉部进流的高效推进装置，为更好地激发泵喷推进器性能，使用SUBOFF艇体艉部与一段椭圆回转面拼接构成前方附体，过渡段平滑连接，以产生推进器入流的湍流伴流场。鉴于本文研究的重点在于探讨所提出的OU−高斯广义表征模型应用于泵喷推进器时的合理性与有效性，因此首先基于简单标准的伴流场进行验证，暂不考虑更复杂的围壳及艉舵结构，以避免其他因素的干扰。泵喷推进器各部件的几何参数如表2所示。
表 2 泵喷推进器几何参数Table 2. Parameters of the pump-jet propulsor参数 数值 导管翼型 NACA0012 导管弦长Lduct/mm 228.7 导管入口端直径Dduct,in/mm 290.6 导管出口端直径Dduct,out/mm 104.8 转子叶片翼型 NACA66 转子叶片数Zrotor 7 转子直径Drotor/mm 208 转子毂径比Dhub/Drotor 0.29 转子叶尖间隙δtip/mm 2 定子叶片翼型 NACA0012 定子叶片数Zstator 9 定子预旋角Astator/(°) 0 定子弦长Lstator/mm 76.2 设置入口位于推进器上游10.24Dduct,in处，出口位于入口下游25Dduct,in处，如图6所示。平均入口速度为3.052 m/s，出口压力为0 Pa。在划分背景域、导管域、定子域和转子域后，考虑转子边界层细化，最终生成2 550万CFD计算网格。采用网格运动方法计算非定常激励，转子绕x轴负方向旋转，转速为Nrot=780 r/min。离散时间步长Δt=1/（360Nrot），每步内迭代18次，计算获得有效数据的时长为1.3 s，对应频率分辨率0.769 2 Hz。在0～500 Hz频段内包含650个频点，能够清晰表征驼峰及谱线的宽带特征，满足后续模型回归分析的需求。
![]()
图 6 出入口边界条件与计算域Figure 6. Boundary conditions at the inlet and outlet, and the computational domain使用上包络平均的方法获取激励宽带谱。研究指出[25]，虽然数据不同的光顺方法和光顺平均点数对功率谱预测精度略有影响，但在合适平均点数区间内，各方法均能反映谱线的宽带衰减趋势、驼峰幅值、宽度和中心频率等特征，且与水筒试验结果展现出较好的一致性。因此，本文选用相邻加权平均的数据光顺法处理原始功率谱，平均点数为30，不同转速下处理方法保持一致。首先，将CFD时域结果分成若干个具有1/4相邻重叠部分的区间，每个区间所含点数为1 760，基于自相关函数的快速傅里叶变换（fast Fourier transform, FFT）结合汉宁窗获得每个区间的功率谱。然后，将各区间功率谱进行平均获得原始功率谱，对原始谱取上包络，获得波动幅值局部最大值，随后采用相邻加权平均方法减少谱线的局部波动。最后，根据式（22）将幅值（N2/Hz）转换到分贝（dB）
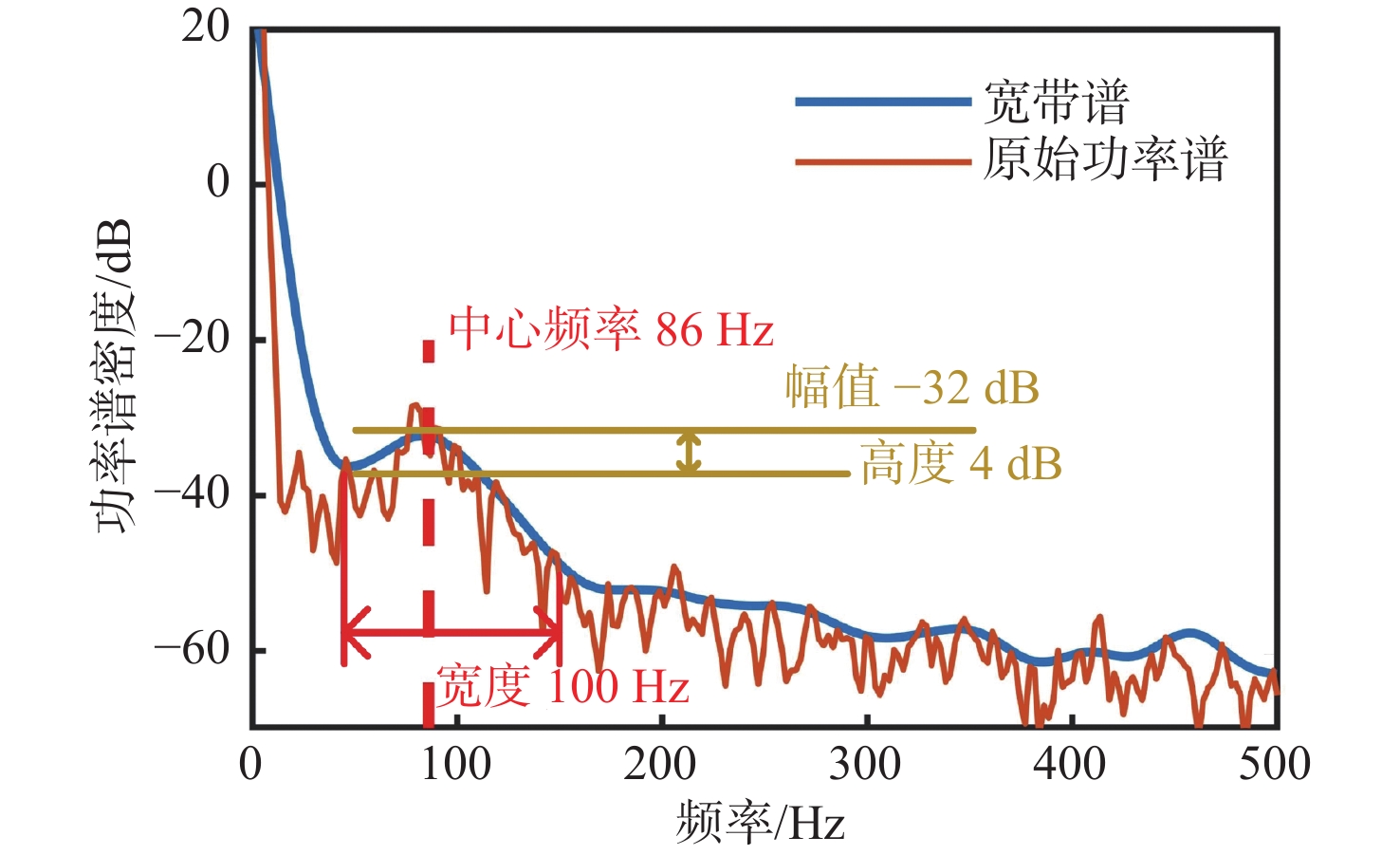
{S_{\left( {{\text{dB}}} \right)}} = 20\lg {S_{\left( {{{\text{N}}^2}/{\text{Hz}}} \right)}} (22) 转速780 r/min的泵喷转子推力功率谱如图7所示，可明显看出功率谱的宽带衰减特性和一阶驼峰。驼峰中心频率在86 Hz附近，接近一阶叶频7×780/60=91 Hz；驼峰幅值为-32 dB，相较周边频段高度为4 dB；驼峰位于[46 146] Hz的频率范围内，宽度约为100 Hz且关于中心频率对称。由于本文采用的计算模型简易，功率谱上未明显出现二阶及以上叶频驼峰，因此可在式（20）中取N=1来仅捕捉一阶驼峰。而在更复杂模型中，驼峰间隔分散，彼此重叠区域小，各个驼峰间无明显干扰，此时可将广义表征模型中的N设为对应值，并使用乘性叠加的高斯函数进行表征。在文中进一步探讨时，不失一般性地仅针对OU过程及一阶高斯函数示例。
![]()
图 7 转子非定常推力功率谱（780 r/min）Figure 7. Unsteady thrust power spectrum of the rotor (780 r/min)3.2 回归分析
基于图7所示的CFD功率谱结果，使用Levenberg-Marquardt算法[28]对式（20）中的6项参数非线性回归，频率区间为0～500 Hz。从第2小节的灵敏度分析可知，OU过程的各参数在频段1和频段3具有更高的灵敏度，而高斯函数的各参数灵敏度集中在频段2。因此，分两步拟合OU过程和高斯函数，以及先OU后高斯的拟合顺序能获得更稳定的拟合效果。为此，首先根据功率谱中驼峰所在位置将整个频率区间分为与图2类似的3个频段，基于频段1和频段3的数据确定表征OU过程的3个参数θ，σ和cw；基于频段2的数据确定表征高斯函数的3个参数cg,1，fg,1和σg,1。为避免仅使用均值曲线评估回归效果的局限性，本文结合95%置信区间准则进行全面评估。
1） 步骤1：识别OU过程
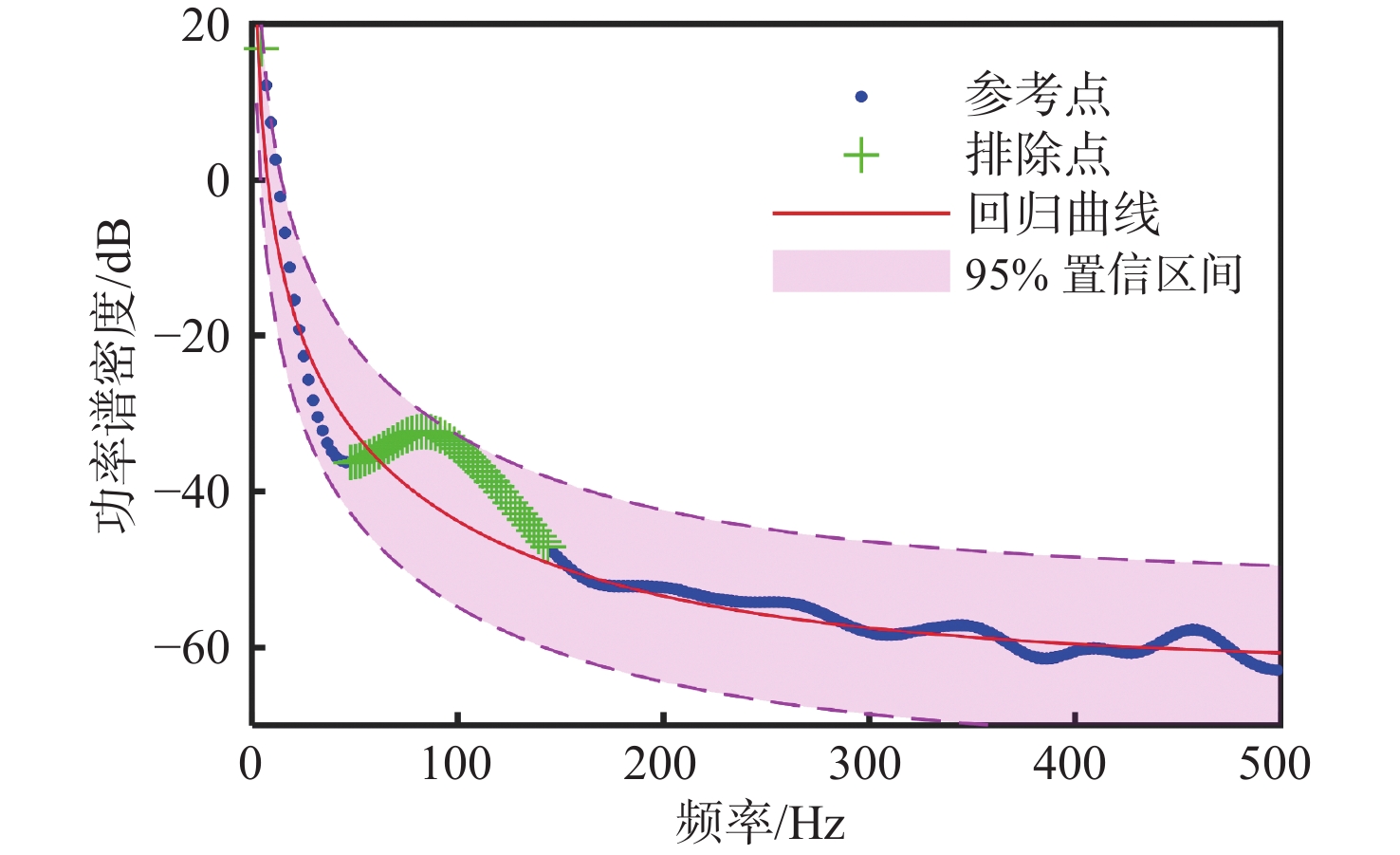
S_{\mathrm{T},\text{OU}}\left(f\right)=\frac{\sigma^2}{\theta^2+f^2}+c_{\text{w}}^2 (23) 参照图7，根据驼峰位置将0～500 Hz频段划分如下的3段主要频段：频段1（0～46 Hz），频段2（46～146 Hz），频段3（146～500 Hz）。鉴于FFT结果具有等频率分辨率性质，功率谱频段1数据远少于频段3，需设定数据点权重为频段1：频段3=20：1来平衡两者在回归曲线中的重要性占比，以保证在频段1中灵敏度较高的参数θ获得更好的回归结果。
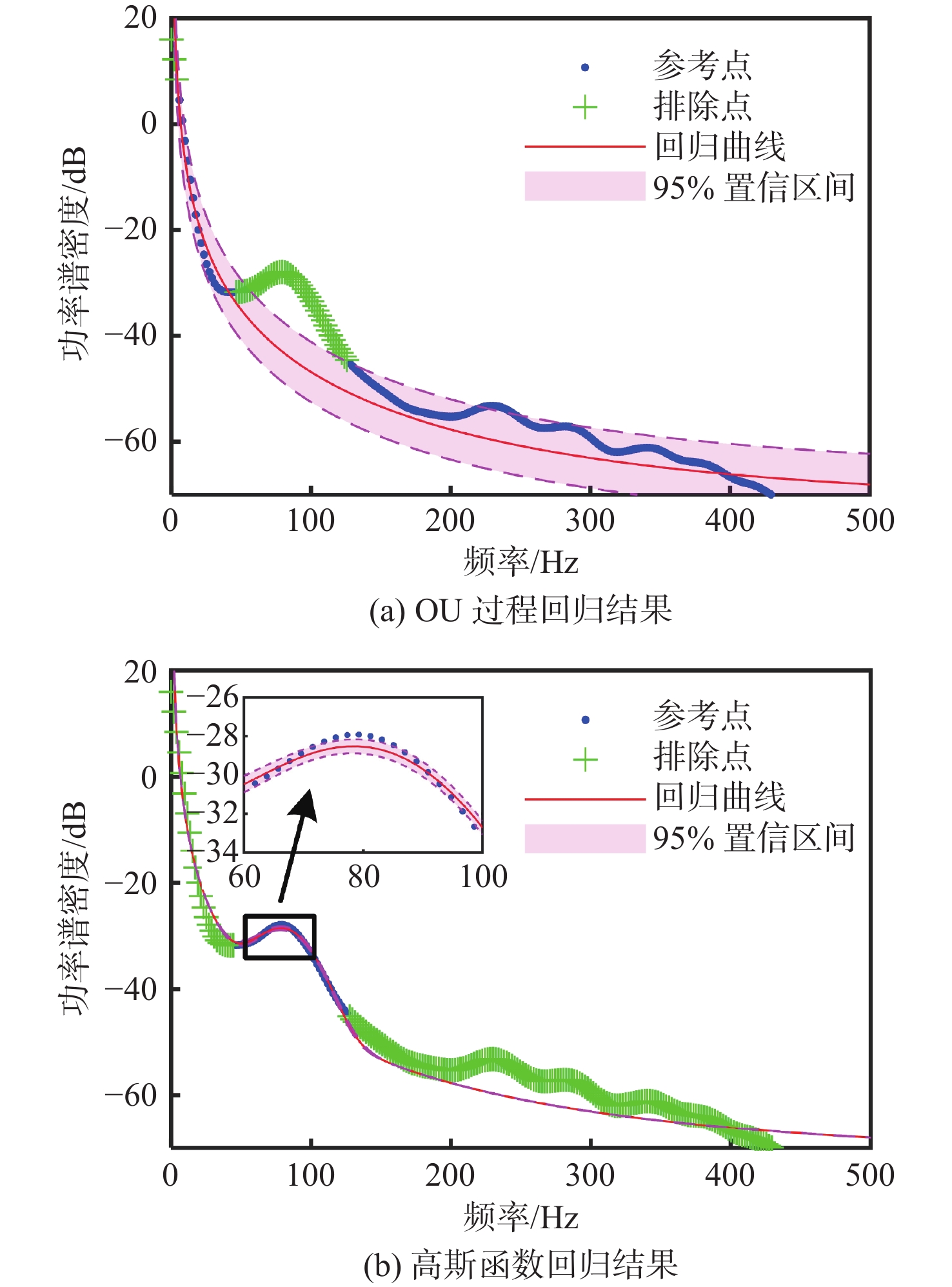
OU过程的回归结果如图8所示，其中蓝色数据点为CFD结果中选用的参考点，绿色数据点为CFD结果中被排除的驼峰，回归均方误差（root mean square error，RMSE）为5.208 1。可以看到，参考点在均值曲线附近小幅波动，但全部落入95%置信区间内，证明本文提出的OU模型用来表征推力功率谱的宽带衰减特性是合理准确的。各参数均值及95%置信区间见表3。
表 3 OU过程回归参数值Table 3. Parameter values of OU process regression参数 回归均值 95%置信区间 θ 2.346 [2.024, 2.872] σ 7.567 [7.071, 8.063] cw 0.026 46 [0.022 1, 0.030 83] 2） 步骤2：在确定OU过程后，识别高斯函数，式（24）中θ，σ和cw为步骤1中已确定的参数
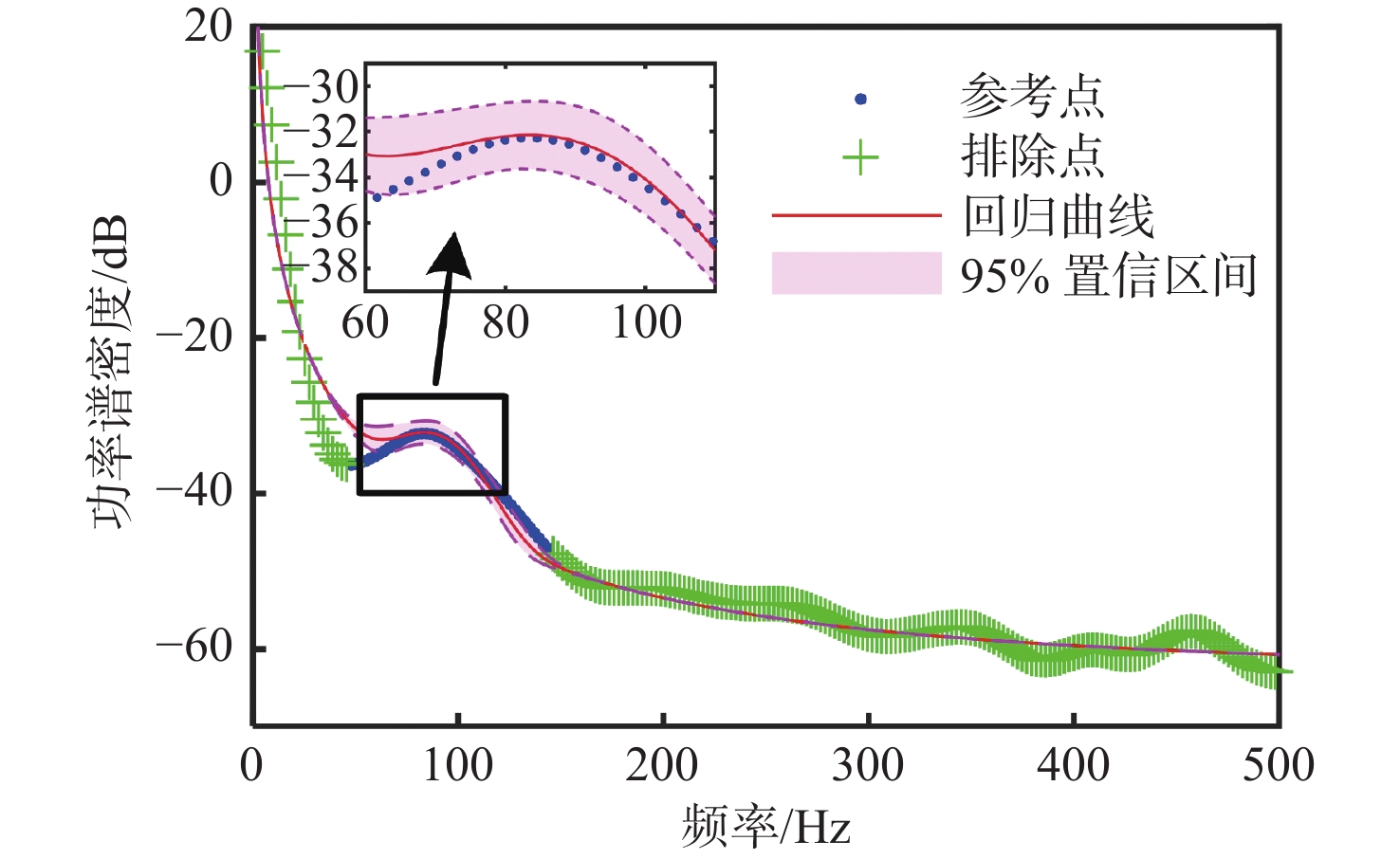
\begin{split} & S_{\mathrm{T},\text{Gauss}}\left(f\right)=\left(\frac{\sigma^2}{\theta^2+f^2}+c_{\text{w}}^2\right)\times \\ &\prod\limits_{i=1}^N\left[c_{\text{g},i}\exp\left(-\frac{\left(f-f_{\text{g},i}\right)^2}{2\sigma_{\text{g},i}^2}\right)+1\right] \end{split} (24) 使用频段2（46～146 Hz）数据进行非线性回归，高斯函数的回归结果如图9所示。可以看出，均值曲线与参考点在驼峰处匹配良好，中心频率附近两者基本一致，RMSE为1.912 3。从95%置信区间来看，高斯函数回归的置信区间宽度较OU过程的更窄，说明高斯函数回归的结果可信度更高。驼峰高于中心频率的多数参考点落入95%置信区间内，而低于中心频率的频段均值曲线偏高，该现象主要是由于OU过程回归误差导致（图8）。各参数均值及95%置信区间见表4。高斯中心频率fg,1=95 Hz与一阶驼峰中心频率86 Hz以及一阶叶频91 Hz接近，说明使用高斯函数表征驼峰是合理的。高斯函数强度cg,1=2.163与驼峰幅值-32 dB对应，标准差σg,1=18.23则与驼峰宽度100 Hz对应。
表 4 高斯函数回归参数值Table 4. Parameter values of Gaussian function regression参数 回归均值 95%置信区间 cg,1 2.163 [1.763, 2.563] fg,1 95 [92.21, 97.79] σg,1 18.23 [15.78, 20.69] 4. 转子转速对模型参数影响规律分析
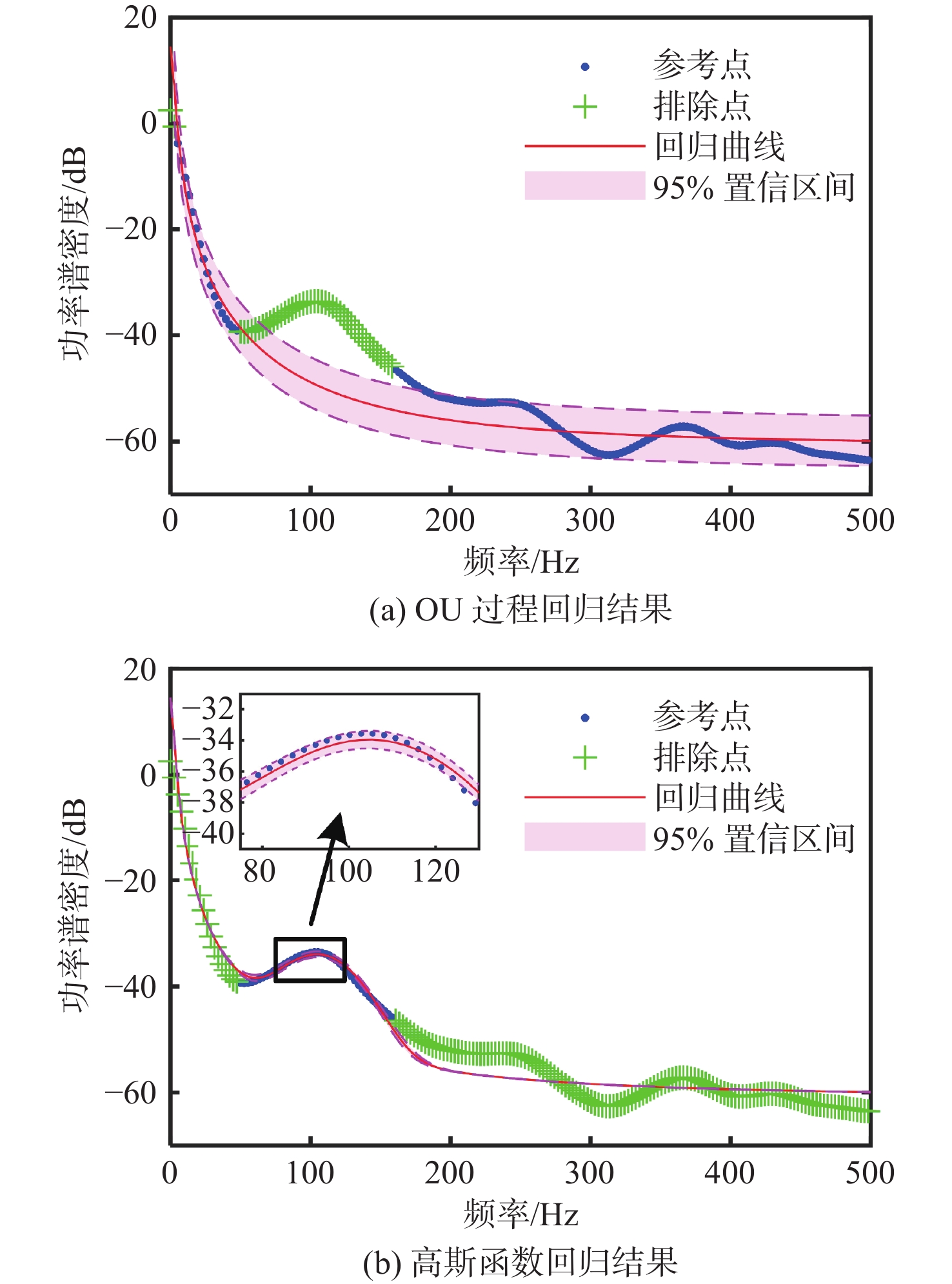
本节验证广义表征模型在不同转速下的泛用性，进一步分析模型各参数随转子转速的变化规律。采取控制变量的思想，在保持湍流进流速度不变的前提下，仅调节转子转速至660 r/min和900 r/min（分别为原780 r/min转速的84.6%和115.4%），采取相同平均点数的上包络平均法获得转子总推力功率谱，如图10所示。对比图7与图10可以发现，随着转速升高，功率谱整体趋势不变，低频段幅值略有降低，而高频段幅值升高，整条曲线更加平缓。一阶驼峰的中心频率跟随叶频移动，其中，660 r/min转速下中心频率降至79 Hz；而900 r/min转速下中心频率升至105 Hz。随转速升高，驼峰变“矮宽”，幅值减小（从−27 dB到−33 dB），宽度增大（从80 Hz到110 Hz），驼峰高度随转速略有增幅（从4 dB到6 dB）。上述驼峰变化意味着，随转速提升，非均匀伴流场在叶频处的非定常激励力能量更加分散，进而导致峰值降低。不同转速下的驼峰参数对比如表5所示。
![]()
图 10 不同转速下转子非定常推力功率谱Figure 10. Unsteady thrust power spectrums of the rotor at different rotational speeds表 5 不同转速下一阶驼峰参数Table 5. First order hump parameters at different rotational speeds转速 660 / （{\text{r}} \cdot {\min ^{ - 1}}） 780 /（{\text{r}} \cdot {\min ^{ - 1}}） 900 /（{\text{r}} \cdot {\min ^{ - 1}}） 一阶叶频/Hz 77 91 105 中心频率/Hz 79 86 105 宽度/Hz 80 100 110 幅值/dB -27 -32 -33 高度/dB 4 4 6 由于转速变化带来的影响主要集中在高频段以及一阶驼峰上，通过第2小节的灵敏度分析可知，这种影响将体现为白噪声强度cw、高斯中心频率fg,1和高斯标准差σg,1的变化。采用3.2小节的两步法分别拟合660 r/min转速与900 r/min转速下的推力功率谱（各回归参数值见表6和表7），结果如图11和图12所示。
表 6 660 r/min转速下模型回归参数值Table 6. Parameter values of model regression at a speed of 660 r/min参数 均值 95%置信区间 θ 2.584 [0.864 3, 4.276] σ 6.583 [6.396, 6.769] cw 0.014 88 [0.012 97, 0.016 79] cg,1 4.887 [4.708, 5.066] fg,1 88.94 [88.44, 89.43] σg,1 18.53 [18.07, 18.98] 表 7 900 r/min转速下模型回归参数值Table 7. Parameter values of model regression at a speed of 900 r/min参数 均值 95%置信区间 θ 2.226 [0.638 2, 3.814] σ 5.202 [5.037, 5.368] cw 0.030 1 [0.028 39, 0.031 82] cg,1 5.382 [1.763, 2.563] fg,1 114.5 [113.5, 115.5] σg,1 24.24 [23.35, 25.13] ![]()
图 11 660 r/min转速下广义表征模型回归结果Figure 11. Regression results of generalized characterization model at a speed of 660 r/min![]()
图 12 900 r/min转速下广义表征模型回归结果Figure 12. Regression results of generalized characterization model at a speed of 900 r/min本文提出的广义表征模型在3种转速下均与CFD结果表现出良好的一致性，模型总RMSE分别为3.44，2.29和2.45。如图8、图9、图11和图12所示，回归误差主要由频段3（尤其是200 Hz以上）的谱线波动贡献。究其原因，一是由于泵喷定子的存在，转子入流将混有定子叶频成分，湍流中水分子速度不再完全符合标准OU过程；二是驼峰数取N=1时，模型忽略了二阶及以上转子叶频驼峰。
不同转速下高斯函数的95%置信区间均具有较窄的宽度，再次证明模型使用高斯函数来表征驼峰的合理性。而除θ外各参数估计均有较窄的置信区间以及较好的可信度，参数θ由于在10～500 Hz的极大频段内灵敏度过低，参数变化对曲线的控制作用过小，因此置信区间较宽。
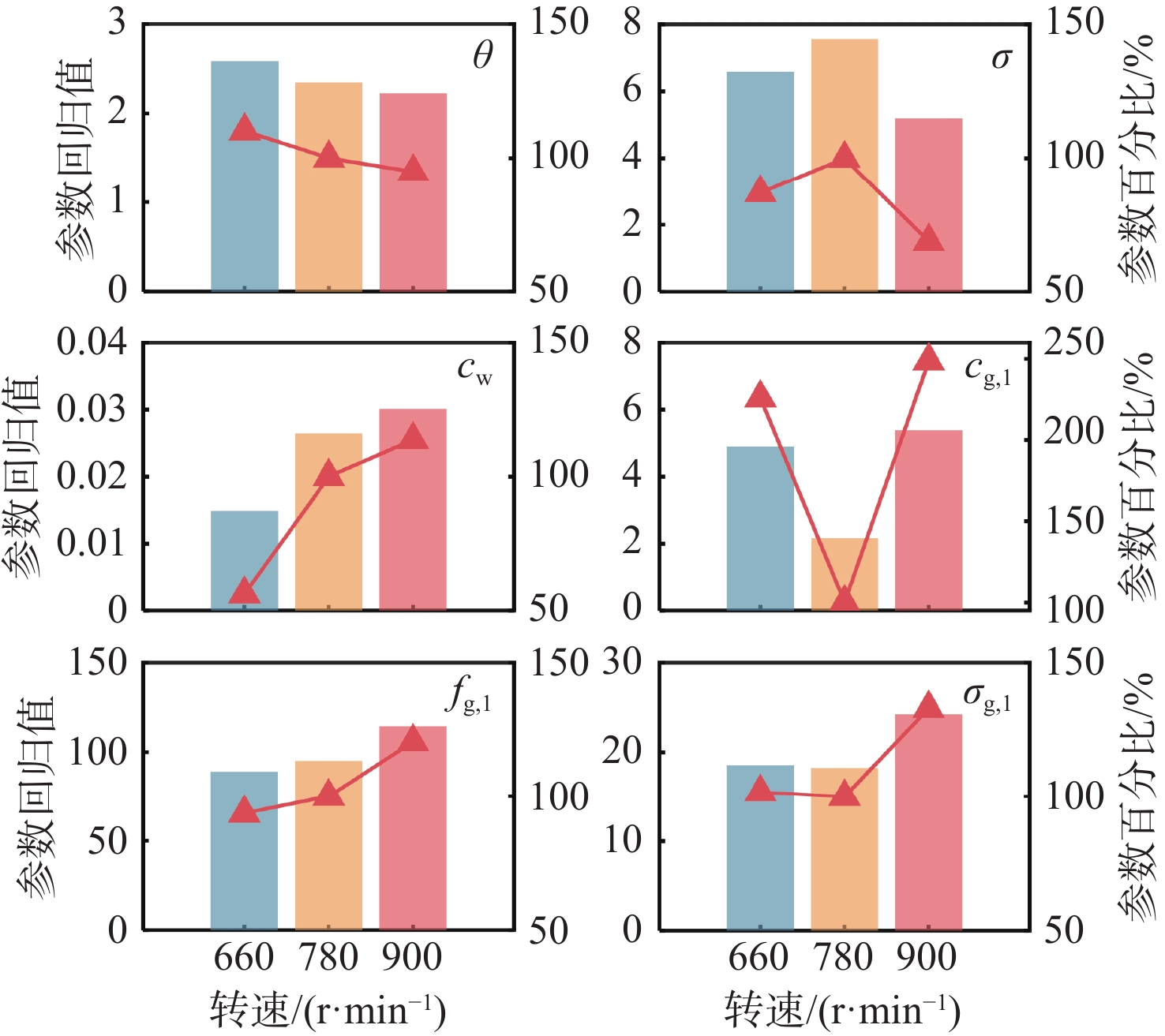
图13展示了模型参数的回归值随转速的变化规律，总结如下：
![]()
图 13 模型参数随转速变化Figure 13. The variation of model parameter values with rotational speed1） 对OU过程而言，转速增加：（1）频段3的幅值增加，致使OU过程以外的白噪声激励强度增加，cw增加；（2）频段2的幅值轻微降低，致使OU过程的强度下降，扩散系数σ略微减少；（3）漂移系数θ的变化较为微小，这主要归因于θ自身灵敏度不显著，与曲线的相关性不强。
2） 对高斯函数而言，转速增加：（1）驼峰高度略有升高，cg,1增加；（2）驼峰中心频率增加，fg,1增加，并且略高于中心频率。该现象可以通过高斯函数与具有宽带衰减特性的OU过程的乘性叠加来解释，OU过程会提高fg,1左侧的低频幅值，同时降低fg,1右侧的高频幅值，导致叠加后谱线的真实中心频率往低频移动，略小于fg,1；（3）驼峰宽度增加，σg,1增加。
由于780 r/min功率谱的回归曲线在低频段（0～46 Hz）内高估了OU过程的幅值（图8和图9），使σ偏大，这进而导致后续步骤2中低估驼峰高度，回归值cg,1偏小。但是，在参数σ和cg,1存在较大误差的情况下，780 r/min的回归曲线仍保持极高的预测精度，说明该广义表征模型具备一定的稳健性，一定范围内个别参数的估计误差能被剩余参数填补。
5. 结 论
本文提出了一种用于描述湍流诱导的螺旋桨/泵喷非定常激励的OU−高斯广义表征模型，能够准确捕捉非定常激励功率谱的宽带衰减特性及各阶叶频驼峰。该模型可为非定常激励反演识别技术提供简洁有效的先验模型约束，亦可为舰艇的声振性能快速评估提供可靠的载荷输入条件。本文分析了模型参数对宽带谱的作用规律，并针对带附体泵喷推进器的轴向推力，基于CFD仿真结果，验证了模型的合理性。通过进一步分析转子转速对模型各参数的影响，验证模型在不同转速下的泛用性。得到如下主要结论：
1） 广义表征模型对各参数具有频率依赖性。在决定OU过程的3个参数θ，σ和cw中，θ的灵敏度较低且主要影响0～10 Hz的较低频段，σ和cw作用于大部分频段，其中cw的影响效果随频率逐渐提升。高斯函数参数cg,1，fg,1和σg,1的作用则集中在驼峰附近，fg,1决定驼峰位置，因此灵敏度最高，cg,1和σg,1的增加均能提高驼峰幅值，但前者在接近驼峰中心频率时作用更加明显，后者则相反。
2） 模型在表征湍流诱导泵喷非定常激励时与CFD展现出一致性。其中，OU过程能够跟踪功率谱中的宽带衰减趋势，高斯函数能够捕捉驼峰。回归曲线及各参数的95%置信区间宽度较窄，表示回归结果具有较高的可信度。
3） 各模型参数均与转子转速呈现相关性，且规律符合灵敏度分析结果。由于转速升高正比作用于驼峰中心频率与驼峰宽度，并附带功率谱高频段幅值提高，因此在相应频段内的高灵敏度参数fg,1，σg,1和cw出现显著增长。而转速对低频段作用微弱，因此主导低频段的参数θ和σ变化不显著。
-
![]()
图 3 OU−高斯模型各参数（N=1）影响规律
Figure 3. Influence law of each parameter in OU-Gaussian model (N=1)
![]()
图 4 OU−高斯过程各模型参数（N=1）的全局灵敏度指数
Figure 4. Global sensitivity indexes of each parameter in OU-Gaussian process model (N=1)
![]()
图 6 出入口边界条件与计算域
Figure 6. Boundary conditions at the inlet and outlet, and the computational domain
![]()
图 7 转子非定常推力功率谱（780 r/min）
Figure 7. Unsteady thrust power spectrum of the rotor (780 r/min)
![]()
图 10 不同转速下转子非定常推力功率谱
Figure 10. Unsteady thrust power spectrums of the rotor at different rotational speeds
![]()
图 11 660 r/min转速下广义表征模型回归结果
Figure 11. Regression results of generalized characterization model at a speed of 660 r/min
![]()
图 12 900 r/min转速下广义表征模型回归结果
Figure 12. Regression results of generalized characterization model at a speed of 900 r/min
![]()
图 13 模型参数随转速变化
Figure 13. The variation of model parameter values with rotational speed
表 1 曲线示意图的参数值
Table 1 Parameter values of the schematic diagram
参数 均值 标准差（按10%均值） θ 3 0.3 σ 5 0.5 cw 0.02 0.002 cg,1 3 0.3 fg,1 100 10 σg,1 20 2 
下载: 导出CSV
表 2 泵喷推进器几何参数
Table 2 Parameters of the pump-jet propulsor
参数 数值 导管翼型 NACA0012 导管弦长Lduct/mm 228.7 导管入口端直径Dduct,in/mm 290.6 导管出口端直径Dduct,out/mm 104.8 转子叶片翼型 NACA66 转子叶片数Zrotor 7 转子直径Drotor/mm 208 转子毂径比Dhub/Drotor 0.29 转子叶尖间隙δtip/mm 2 定子叶片翼型 NACA0012 定子叶片数Zstator 9 定子预旋角Astator/(°) 0 定子弦长Lstator/mm 76.2
下载: 导出CSV
表 3 OU过程回归参数值
Table 3 Parameter values of OU process regression
参数 回归均值 95%置信区间 θ 2.346 [2.024, 2.872] σ 7.567 [7.071, 8.063] cw 0.026 46 [0.022 1, 0.030 83]
下载: 导出CSV
表 4 高斯函数回归参数值
Table 4 Parameter values of Gaussian function regression
参数 回归均值 95%置信区间 cg,1 2.163 [1.763, 2.563] fg,1 95 [92.21, 97.79] σg,1 18.23 [15.78, 20.69]
下载: 导出CSV
表 5 不同转速下一阶驼峰参数
Table 5 First order hump parameters at different rotational speeds
转速 660 / （{\text{r}} \cdot {\min ^{ - 1}}） 780 /（{\text{r}} \cdot {\min ^{ - 1}}） 900 /（{\text{r}} \cdot {\min ^{ - 1}}） 一阶叶频/Hz 77 91 105 中心频率/Hz 79 86 105 宽度/Hz 80 100 110 幅值/dB -27 -32 -33 高度/dB 4 4 6
下载: 导出CSV
表 6 660 r/min转速下模型回归参数值
Table 6 Parameter values of model regression at a speed of 660 r/min
参数 均值 95%置信区间 θ 2.584 [0.864 3, 4.276] σ 6.583 [6.396, 6.769] cw 0.014 88 [0.012 97, 0.016 79] cg,1 4.887 [4.708, 5.066] fg,1 88.94 [88.44, 89.43] σg,1 18.53 [18.07, 18.98]
下载: 导出CSV
表 7 900 r/min转速下模型回归参数值
Table 7 Parameter values of model regression at a speed of 900 r/min
参数 均值 95%置信区间 θ 2.226 [0.638 2, 3.814] σ 5.202 [5.037, 5.368] cw 0.030 1 [0.028 39, 0.031 82] cg,1 5.382 [1.763, 2.563] fg,1 114.5 [113.5, 115.5] σg,1 24.24 [23.35, 25.13]
下载: 导出CSV
-
[1] 华宏星, 俞强. 船舶艉部激励耦合振动噪声机理研究进展与展望[J]. 中国舰船研究, 2017, 12(4): 6–16. doi: 10.3969/j.issn.1673-3185.2017.04.002 HUA H X, YU Q. Structural and acoustic response due to excitation from ship stern: overview and suggestions for future research[J]. Chinese Journal of Ship Research, 2017, 12(4): 6–16 (in Chinese). doi: 10.3969/j.issn.1673-3185.2017.04.002
[2] MOLLAND A F, TURNOCK S R. A propeller thrust and torque dynamometer for wind tunnel models[J]. Strain, 2002, 38(1): 3–10. doi: 10.1046/j.0039-2103.2002.00001.x
[3] TONG X D, CHEN H Y, CHEN Y. Low frequency broadband noise radiated by highly skewed propeller ingesting inflow turbulence[J]. Journal of Sound and Vibration, 2021, 490: 115709. doi: 10.1016/j.jsv.2020.115709
[4] ZHANG Z G, WEI Y, TONG X D, et al. Simultaneous identification of propeller fluctuating forces and unknown parameters based on a Bayesian inversion approach[J]. Ocean Engineering, 2024, 312: 119234. doi: 10.1016/j.oceaneng.2024.119234
[5] QIN D H, STALNOV O, HUANG X. Numerical investigation of parameters influencing the turbulence-ingesting noise of a ten-bladed propeller[J]. Ocean Engineering, 2024, 300: 117237. doi: 10.1016/j.oceaneng.2024.117237
[6] 王旭. 基于改进的LMS算法动载荷识别应用研究[D]. 哈尔滨: 哈尔滨工程大学, 2019. WANG X. Dynamic load identification based on improved LMS algorithm applied research[D]. Harbin: Harbin Engineering University, 2019 (in Chinese).
[7] DING Y, LAW S S, WU B, et al. Average acceleration discrete algorithm for force identification in state space[J]. Engineering Structures, 2013, 56: 1880–1892. doi: 10.1016/j.engstruct.2013.08.004
[8] KABANIKHIN S I. Definitions and examples of inverse and ill-posed problems[J]. Journal of Inverse and Ill-Posed Problems, 2008, 16(4): 317–357. doi: 10.1515/JIIP.2008.019
[9] ZHANG Z G, ZHONG Y C, DUAN N Y, et al. Indirect measurement of propeller fluctuating forces using an inverse analysis: Numerical and experimental studies[J]. Ocean Engineering, 2023, 285: 115337. doi: 10.1016/j.oceaneng.2023.115337
[10] WEI Y, ZHONG Y, WEI B, et al. Dynamic forces estimation of structural systems by using a Bayesian regularization method[C]//Proceedings of the 28th International Congress on Sound and Vibration. Singapore: The International Institute of Acoustics and Vibration, 2022.
[11] LI Q F, LU Q H. A revised time domain force identification method based on Bayesian formulation[J]. International Journal for Numerical Methods in Engineering, 2019, 118(7): 411–431. doi: 10.1002/nme.6019
[12] NAETS F, CUADRADO J, DESMET W. Stable force identification in structural dynamics using Kalman filtering and dummy-measurements[J]. Mechanical Systems and Signal Processing, 2015, 50-51: 235–248. doi: 10.1016/j.ymssp.2014.05.042
[13] SEVIK M. Sound radiation from a subsonic rotor subjected to turbulence[R]. [S. l. ]: NASA, 1974.
[14] MARTINEZ R. Asymptotic theory of broadband rotor thrust, part I: manipulations of flow probabilities for a high number of blades[J]. Journal of Applied Mechanics, 1996, 63(1): 136–142. doi: 10.1115/1.2787188
[15] BLAKE W K. Mechanics of flow-induced sound and vibration, volume 1: general concepts and elementary sources[M]. Waltham: Elsevier, 2012.
[16] KIRSCHNER I N, CORRIVEAU P J, MUENCH J D, et al. Validation of an In-air acoustic radiation model using wind-tunnel measurements[C]//Proceedings of the ASME Symposium on Flow Noise Modeling, Measurement, and Control, NCA 15ASME Symposium on Flow Noise Modeling, Measurement, and Control, NCA. ASME, 1993.
[17] ZHANG L T, CUI W, ZHAO L, et al. State augmentation method for buffeting responses of wind-sensitive structures in wind environments with large turbulence intensity[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2023, 240: 105498. doi: 10.1016/j.jweia.2023.105498
[18] ONNEN D, NEUHAUS L, PETROVIĆ V, et al. Dynamic wake conditions tailored by an active grid in the wind tunnel[J]. Journal of Physics: Conference Series, 2024, 2767: 042038. doi: 10.1088/1742-6596/2767/4/042038
[19] ALLI O D, ADEGBOLA J O, AKINGBADE T O, et al. Stochastic vibrations based on transonic flutter suppression of a three-dimensional elastic wing via active disturbance rejection control[J]. Adeleke University Journal of Engineering and Technology, 2024, 7(1): 107–115.
[20] 康伟. 湍流诱发弹性螺旋桨—轴系的随机振动响应及控制方法研究[D]. 上海: 上海交通大学, 2019. KANG W. Research on random vibration response and control method of the elastic propeller-shafting induced by turbulence[D]. Shanghai: Shanghai Jiao Tong University, 2019 (in Chinese).
[21] UHLENBECK G E, ORNSTEIN L S. On the theory of the Brownian motion[J]. Physical Review, 1930, 36(5): 823–841. doi: 10.1103/PhysRev.36.823
[22] LANGEVIN P, OTHERS. Sur la théorie du mouvement brownien[J]. CR Acad. Sci. Paris, 1908, 146: 530-533(in French).
[23] LEDOUX J, RIFFO S, SALOMON J. Analysis of the blade element momentum theory[J]. SIAM Journal on Applied Mathematics, 2021, 81(6): 2596–2621. doi: 10.1137/20M133542X
[24] KAREEM A, TOGNARELLI M A, GURLEY K R. Modeling and analysis of quadratic term in the wind effects on structures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74-76: 1101–1110. doi: 10.1016/S0167-6105(98)00101-9
[25] 师帅康. 泵喷推进器非定常宽带力及流致振动特性研究[D]. 上海: 上海交通大学, 2023. SHI S K. Research on the non-steady broadband force flow induced vibration characteristics of pump jet propulsion[D]. Shanghai: Shanghai Jiao Tong University, 2019 (in Chinese).
[26] SOBOL’ I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1-3): 271–280. doi: 10.1016/S0378-4754(00)00270-6
[27] GROVES N C, HUANG T T, CHANG M S. Geometric characteristics of DARPA SUBOFF models (DTRC Model Nos. 5470 and 5471)[R]. Bethesda: David Taylor Research Centre, 1989.
[28] GAVIN H P. The Levenberg-Marquardt algorithm for nonlinear least squares curve-fitting problems[D]. Durham: Department of Civil and Environmental Engineering, Duke University, 2019.
计量
- 文章访问数: 55
- HTML全文浏览量: 17
- PDF下载量: 2
