Affine formation maneuver control for multiple autonomous surface vehicles under event-triggered inter-vehicle communication
-
摘要:目的
针对通信资源受限的水面自主航行器(ASV)编队问题,提出基于事件触发的ASVs分布式仿射编队控制算法。
方法首先,通过应用仿射变换理论,为ASVs设计一种更简便的编队操纵方式,使编队内的智能体可以完成缩放、平移、旋转和剪切等整体编队动作,以及这些动作变换之间的相互组合;然后,提出一种新的事件触发机制,让ASVs仅在满足触发条件的时刻才与邻居个体进行通信,以节省通信和计算资源,并避免Zeno行为。
结果通过稳定性分析,证明了闭环误差的收敛性及系统的最终有界稳定性;通过仿真分析,证明了编队能够完成多样化的几何变换,同时事件触发机制降低了通信频率并节省了78%的通信资源,有效减少了能量消耗。
结论该算法通过仿射变换提高了编队的灵活性,并通过降低通信频率节约了能量消耗,研究成果可为ASVs编队的优化设计提供参考。
-
关键词:
- 仿射变换 /
- 事件触发机制 /
- 编队控制 /
- 水面自主航行器(ASV) /
- 动态面控制
Abstract:ObjectivesThis study aims to develop a formation maneuver control mechanism for multiple autonomous surface vehicles (ASVs) suffering from external and parameter uncertainties. Meanwhile, considering the limitation of resources equipped on ASVs, it is preferred to design a resource-saving formation control algorithm.
MethodsFirstly, affine transformation is embedded into our control scheme, thus ASVs can achieve rotation, scaling, translation and shearing motion as a union, as well as the combination of these motions. By virtue of this operation, formation can be flexibility maneuvered in a distributed manner. Secondly, to handle with limited communication resources, an event-triggered mechanism is proposed and incorporated into our algorithm. Wherein, by evaluating the triggering condition, vehicles merely communicate with their neighbors if necessary, i.e., when the predesigned triggering condition is satisfied. Benefited from this process, inter-vehicle communication frequency can be effectively reduced and resources are utilized more effectively.
ResultsStability analysis demonstrates the convergence of all closed-loop error signals to a compact set, ensuring the ultimate boundedness of the closed-loop system. Simulation results verify that the proposed algorithm enables the formation to achieve diverse geometric transformations, while the event-triggered mechanism reduces the communication frequency, resulting in an 78% saving in communication resources and energy consumption.
ConclusionsThe proposed algorithm enhances the flexibility of ASV formations through the use of affine transformations and reduces energy consumption by lowering the communication frequency. The research results can provide reference for the optimization design of ASVs formation.
-
0. 引 言
随着海洋资源开发、海上安全防卫及环境监测任务的日益复杂化,水面自主航行器(autonomous surface vehicle,ASV)编队技术因其协同高效性、任务鲁棒性及环境适应性,已成为海洋工程与智能控制领域的研究热点[1-4]。在军事领域,多ASV编队可以执行协同侦察、区域封锁及战术干扰等任务;在民用领域,其广泛应用于海洋资源勘探、海上搜救及水质监测等场景[5-6]。然而,在实际应用中,ASV编队需面对复杂多变的海洋环境(例如洋流扰动、障碍物分布密集)及严格的资源约束(例如通信带宽有限、机载计算能力不足),这对 编队控制的灵活性、实时性及鲁棒性提出了更高的要求[7-9]。因此,设计高效的ASV编队控制算法,将有助于提升ASV编队性能,从而快速适应复杂、动态且充满不确定因素的战场环境。
传统的编队控制方法一般基于固定几何约束,即要求编队成员严格保持固定的相对位置与角度。例如,Zhang等[8]采用领航−跟随策略,通过预设的几何关系实现了编队跟踪,但其队形调整仍需依赖全局信息,故难以适应动态任务需求;Arrichiello等[10]提出了基于虚拟结构的分布式控制算法,虽然降低了通信依赖性,但仍局限于平移运动,而无法实现缩放、旋转等仿射变换,所以大幅限制了自主航行器编队执行任务时的灵活性。此外,现有的研究成果大多假设通信资源充足,并采用固定频率的数据交换[11],导致在狭窄带宽或能源受限场景下易引发网络拥塞与能量枯竭问题。Peng等[12-14]和Huang等[15]研究了分布式控制算法,以减轻通信负担。虽然上述方法简化了通信网络结构,但系统需以固定频率来更新状态信息,所以仍存在网络堵塞及能源浪费等问题。
对于节约通信能源消耗而言,降低ASV之间的通信频率至关重要。与此同时,较低的通信频率可以降低无人航行器通信网络的数据传输负担,由此降低信息堵塞及丢包等风险。近年来,事件触发机制通过仅在系统状态超过预设阈值时触发通信,为降低通信频率提供了新的思路[16]。然而,现有的事件触发机制研究成果大多集中于线性多智能体系统,而ASV的欠驱动特性与强非线性动力学(例如科里奥利力、阻尼效应)导致难以直接应用传统的事件触发策略。具体而言,ASV仅通过推进器与舵实现三自由度(纵荡、横荡及艏摇)控制,其动力学模型存在高度耦合性与非对称性,故其控制器设计需兼顾运动学与动力学的协同优化。
基于此,本文拟针对具有非线性动力学的二阶ASV编队系统,在交互通信拓扑下提出一种基于事件触发的分布式仿射编队控制算法。首先,通过嵌入仿射变换理论,使编队可以实时完成平移、旋转、缩放及剪切等几何变换;与传统的固定队形控制相比,仿射变换允许编队根据任务需求来动态调整整体构型(例如在障碍物规避中收缩队形或在狭窄水域中旋转队形),从而显著提升环境适应能力。然后,将设计一种动态阈值触发条件,仅当跟踪误差超过自适应阈值时才触发邻居间通信;该策略在保证系统稳定性的前提下,可以降低78%的通信频率,且可通过严格的Zeno行为排除证明,从而避免有限时间内无限次触发的风险。最后,将针对反步法中高阶微分导致的“微分爆炸”问题,引入动态面控制技术,并通过一阶滤波器平滑虚拟控制信号;同时,将进一步结合径向基神经网络与最小参数学习法,在线逼近模型不确定性及外界干扰,最终显著提升系统的鲁棒性。
1. 理论知识与问题描述
1.1 ASV数学模型
针对在水平面运动的N艘ASV编队系统,引入2个相关的坐标系(即固定坐标系OXY和随体坐标系ObXbYb)来描述其运动情况,将每艘ASV的动力学和非线性运动学模型简化为
\left\{ \begin{gathered} {{\dot {\boldsymbol{p}}}_i} = {{\boldsymbol{q}}_i} \\ {{\dot {\boldsymbol{q}}}_i} = {{\boldsymbol{f}}_1}\left( {{u_i},{v_i},{r_i}} \right) + {\hbar _i}{\left[ {{{\boldsymbol{\tau}} _{{\text{u}}i}},{\tau _{{\text{v}}i}}} \right]^{\text{T}}} + {\boldsymbol{\tau }}_i^{\text{d}} \\ {{\dot \psi }_i} = {r_i} \\ {{\dot r}_i} = {f_2}\left( {{u_i},{v_i},{r_i}} \right) + {\tau _{{\text{r}}i}}/{m_{33i}} + \tau _i^{\text{r}} \\ \end{gathered} \right. (1) \begin{split} & \qquad\qquad\qquad {{\boldsymbol{f}}_1}\left( {{u_i},{v_i},{r_i}} \right) = \\&\;\;\; \left[ {\begin{array}{*{20}{c}} {\left( {{m_{22}}{v_i}{r_i} - {d_{11}}{u_i}} \right){\text{cos}}{\psi _i}/{m_{11}} - {u_i}\sin {\psi _i} - } \\ {\left( {{m_{22}}{v_i}{r_i} - {d_{11}}{u_i}} \right){\text{sin}}{\psi _i}/{m_{11}} + {u_i}\cos {\psi _i} + } \end{array}} \right. \\& {\text{ }}\left. {\begin{array}{*{20}{c}} {\left( { - {m_{11}}{u_i}{r_i} - {d_{22}}{v_i}} \right)\sin {\psi _i}/{m_{22}} - {v_i}\cos {\psi _i}} \\ {\left( { - {m_{11}}{u_i}{r_i} - {d_{22}}{v_i}} \right)\cos {\psi _i}/{m_{22}} - {v_i}\sin {\psi _i}} \end{array}} \right] \end{split} (2) {f_2}\left( {{u_i},{v_i},{r_i}} \right) = \left( {\left( {{m_{11}} - {m_{22}}} \right){u_i}{v_i} - {d_{33}}{r_i}} \right)/{m_{33}} (3) {\hbar _i} = \left[ \begin{matrix} {\dfrac{{{\text{cos}}{\psi _i}}}{{{m_{11i}}}}} & {\dfrac{{ - {\text{sin}}{\psi _i}}}{{{m_{22i}}}}}\\ {\dfrac{{{\text{sin}}{\psi _i}}}{{{m_{11i}}}}} & {\dfrac{{{\text{cos}}{\psi _i}}}{{{m_{22i}}}}} \end{matrix} \right] (4) 式中:{{\boldsymbol{p}}_i} = {\left[ {{x_i},{y_i}} \right]^{\text{T}}},为第i艘ASV在固定坐标系 OXY 下的位置向量,其中i=1,2,…,N; {{\boldsymbol{q}}}_{i}= {\left[{u}_{i}\mathrm{cos}{\psi }_{i}-{v}_{i}\mathrm{sin}{\psi }_{i},{u}_{i}\mathrm{sin}{\psi }_{i}+{v}_{i}\mathrm{cos}{\psi }_{i}\right]}^{\text{T}} ,为第i艘ASV在随体坐标系下的速度向量,其中 {u_i} 和 {v_i} 分别为前向速度和横向速度, {\psi _i} 为艏向角; {{\boldsymbol{f}}_1}\left( {{u_i},{v_i},{r_i}} \right) 为模型的未建模动态,其中 {r_i} 为艏向角速度; {\hbar _i}{\left[ {{\tau _{{\text{u}}i}},{\tau _{{\text{v}}i}}} \right]^{\text{T}}} 为固定坐标系与随体坐标系之间的转换矩阵,其中 {\tau _{{\text{u}}i}} , {\tau _{{\text{v}}i}} 均为控制输入; {\boldsymbol{\tau }}_i^{\text{d}} = {\left[ {\tau _i^{\text{u}},\tau _i^{\text{v}}} \right]^{\text{T}}} , \tau _i^{\text{r}} 为外界干扰,均为外界干扰; {f_2}\left( {{u_i},{v_i},{r_i}} \right) 为模型的未建模动态; {\tau _{{\text{r}}i}} 为控制输入; {m_{33i}} 为偏航运动的总转动惯量; {m_{11}} , {m_{22}} , {m_{33}} 为ASV的惯性质量; {d_{11}} , {d_{22}} , {d_{33}} 均为水动力阻尼系数; {m_{11i}} , {m_{22i}} 为纵荡、横荡方向的总质量;为简化计算,令 {{\boldsymbol{\tau }}_i} = \left[ {{\tau _{{\text{u}}i}},{\tau _{{\text{v}}i}}} \right] , \hbar = {\left( {\hbar _{\text{1}}^{\text{T}},...,\hbar _N^{\text{T}}} \right)^{\text{T}}} 。
1.2 仿射编队理论
ASV集群之间的底层信息交互可以采用无向图 \mathcal{G} = \left( {\mathcal{V},\mathcal{E}} \right) 予以表示,其中节点集 \mathcal{V} = \left\{ {1,...,N} \right\} ,边集 \mathcal{E} \subset \mathcal{V} \times \mathcal{V} 。如果 \left( {i,j} \right) \in \mathcal{E} ,则表明节点i可以接收节点j的数据信息,其中j=1,2,…,N。 {\mathcal{N}_i} = \left\{ {j \in \mathcal{V}:\left( {i,j} \right) \in \mathcal{E}} \right\} ,为节点i的入邻居集合。邻接矩阵 \mathring{A} = \left[ {{a_{ij}}} \right] \in {\mathbb{R}^{N \times N}} ,当 \left( {i,j} \right) \in \mathcal{E} 时, {a_{ij}} > 0 ,否则 {a_{ij}} = 0 ,其中 \mathbb{R} 为实数空间。将无向图 \mathcal{G} 的拉普拉斯矩阵定义为 {\boldsymbol{L}} = \left[ {{l_{ij}}} \right] \in {\mathbb{R}^{N \times N}} ,当 i \ne j 时, {l_{ij}} = - {a_{ij}} ,否则 {l_{ii}} = \sum\limits_{j = 1}^N {{a_{ij}}} 。
在空间 {\mathbb{R}^d} 内考虑由N艘ASV组成的领导−跟随者编队系统,其中d 为空间维度。假设d \geqslant 2且N \geqslant d + 2,设定前 {N_{\text{L}}} 艘ASV为领导者,剩下的 {N_{\text{F}}} = N - {N_{\text{L}}} 艘ASV为跟随者,且 {\mathcal{V}_{\text{L}}} 和 {\mathcal{V}_F} = \mathcal{V}\backslash {\mathcal{V}_{\text{L}}} 分别为领导者集合与跟随者集合。定义 {\boldsymbol{p}} = {( {{\boldsymbol{p}}_{\text{1}}^{\text{T}},...,{\boldsymbol{p}}_N^{\text{T}}} )^{\text{T}}} \in {\mathbb{R}^{dN}} 为N艘ASV的位置集合, {{\boldsymbol{p}}_{\text{L}}} = {( {{\boldsymbol{p}}_{\text{1}}^{\text{T}},{\boldsymbol{p}}_2^{\text{T}},...,{\boldsymbol{p}}_{{N_{\text{L}}}}^{\text{T}}} )^{\text{T}}} 和 {p}_{\text{F}}={({p}_{{N}_{\text{L}}\text{+1}}^{\text{T}},{p}_{{N}_{\text{L}}\text{+2}}^{\text{T}},\mathrm{...},{p}_{N}^{\text{T}})}^{\text{T}} 分别为领导者位置集合与跟随者位置集合, {\boldsymbol{\psi }} = {( {{\boldsymbol{\psi }}_{\text{L}}^{\text{T}},{\boldsymbol{\psi }}_{\text{F}}^{\text{T}}} )^{\text{T}}} 为艏向角集合, {\psi _{\text{L}}} = {( {\psi _{\text{1}}^{\text{T}},\psi _2^{\text{T}},...,\psi _{{N_{\text{L}}}}^{\text{T}}} )^{\text{T}}} 和 {\psi }_{\text{F}}={({\psi }_{{N}_{\text{L}}\text{+1}}^{\text{T}},{\psi }_{{N}_{\text{L}}\text{+2}}^{\text{T}},\mathrm{...},{\psi }_{N}^{\text{T}})}^{\text{T}} 分别为领导者艏向角与跟随者艏向角集合,并定义3个假设,具体如下:
假设1[18]:由N艘ASV构成的无向图 \mathcal{G} 至少包含 d + 1 个领导者,并且跟随者集合中的每个跟随者均从领导者集合 d + 1 中可达。
假设2[18]:如果给定的N艘ASV的标称队形r满足 \left\{ {{r_i}} \right\}_{i = 1}^N ,则其可在空间 {\mathbb{R}^d} 内仿射张成。
假设3[19-20]:如果给定的 {N_{\text{L}}} 个领导者的标称队形 {r_{\text{L}}} 满足 {\left\{ {{r_i}} \right\}_{i \in {\mathcal{V}_{\text{L}}}}} ,则其可在空间 {\mathbb{R}^d} 内仿射张成。
对于ASV集群系统,其各边 \left( {i,j} \right) \in \mathcal{E} 的应力 {\left\{ {{\omega _{ij}}} \right\}_{\left( {i,j} \right) \in \mathcal{E}}} 是一组标量,当第i艘ASV与第j艘ASV之间为吸引力时, {\omega _{ij}} > 0 ;当为排斥力时, {\omega _{ij}} < 0 ;其他情况下, {\omega _{ij}} = 0 。应力 {\omega _{ij}} 与编队之间的关系[21]可描述为
\sum\limits_{j \in {\mathcal{N}_i}} {{\omega _{ij}}\left( {{{\boldsymbol{p}}_j} - {{\boldsymbol{p}}_i}} \right) = 0,\;i} \in \mathcal{V} (5) {\left\{ {{\omega _{ij}}} \right\}_{\left( {i,j} \right) \in \mathcal{E}}} 可以表达为如下的应力矩阵 {\left[ {\boldsymbol{\varOmega }} \right]_{ij}} :
{\left[ {\boldsymbol{\varOmega }} \right]_{ij}} = \left\{ \begin{aligned} & 0,&& i \ne j,\left( {i,j} \right) \notin \mathcal{E} \\& - {\omega _{ij}},&& i \ne j,\left( {i,j} \right) \in \mathcal{E} \\& \sum\nolimits_{\ell \in {\mathcal{N}_i}} {\omega _{i\ell }},&& i = j \end{aligned} \right. (6) 式中, {\omega _{i\ell }} 为边 \left( {i,\ell } \right) 的权重值,其中\ell 为无向图中与结点i相邻的邻居结点。
结合式(6),式(5),得
\left( {{\boldsymbol{\varOmega }} \otimes {{\boldsymbol{I}}_d}} \right){\boldsymbol{p}} = 0 (7) 式中, {{\boldsymbol{I}}_d} 为d维单位矩阵。
对于由N艘ASV组成的编队系统,其应力矩阵 {\boldsymbol{\bar \varOmega }} 为
{\boldsymbol{\bar \varOmega }} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{\varOmega }}_{{\text{LL}}}}}&{{{\boldsymbol{\varOmega }}_{{\text{L}}F}}} \\ {{{\boldsymbol{\varOmega }}_{{\text{FL}}}}}&{{{\boldsymbol{\varOmega }}_{{\text{FF}}}}} \end{array}} \right] \otimes {{\boldsymbol{I}}_d} = \left[ {\begin{array}{*{20}{c}} {{{{\boldsymbol{\bar \varOmega }}}_{{\text{LL}}}}}&{{{{\boldsymbol{\bar \varOmega }}}_{{\text{L}}F}}} \\ {{{{\boldsymbol{\bar \varOmega }}}_{{\text{FL}}}}}&{{{{\boldsymbol{\bar \varOmega }}}_{{\text{FF}}}}} \end{array}} \right] (8) 式中: {{\boldsymbol{\varOmega }}_{{\text{LL}}}} \in {\mathbb{R}^{d{N_{\text{L}}} \times d{N_{\text{L}}}}} ,为领导者之间的应力矩阵,其中 {\mathbb{R}^{d{N_{\text{L}}} \times d{N_{\text{L}}}}} 为 {{\boldsymbol{\varOmega }}_{{\text{LL}}}} 的维度; {{\boldsymbol{\varOmega }}_{{\text{FL}}}} \in {\mathbb{R}^{d{N_{\text{F}}} \times d{N_{\text{L}}}}} ,为跟随者与领导者之间的应力矩阵,其中 {\mathbb{R}^{d{N_{\text{F}}} \times d{N_{\text{L}}}}} 为 {{\boldsymbol{\varOmega }}_{{\text{FL}}}} 的维度; {{\boldsymbol{\varOmega }}_{{\text{LF}}}} \in {\mathbb{R}^{d{N_{\text{L}}} \times d{N_{\text{F}}}}} 为领导者与跟随者之间的应力矩阵,其中 {\mathbb{R}^{d{N_{\text{L}}} \times d{N_{\text{F}}}}} 为 {{\boldsymbol{\varOmega }}_{{\text{LF}}}} 的维度; {{\boldsymbol{\varOmega }}_{{\text{FF}}}} \in {\mathbb{R}^{d{N_{\text{F}}} \times d{N_{\text{F}}}}} 为跟随者之间的应力矩阵,其中 {\mathbb{R}^{d{N_{\text{F}}} \times d{N_{\text{F}}}}} 为 {{\boldsymbol{\varOmega }}_{{\text{FF}}}} 的维度; {{\boldsymbol{\bar \varOmega }}_{{\text{LL}}}} = {{\boldsymbol{\varOmega }}_{{\text{LL}}}} \otimes {{\boldsymbol{I}}_d} , {{\boldsymbol{\bar \varOmega }}_{{\text{LF}}}} = {{\boldsymbol{\varOmega }}_{{\text{LF}}}} \otimes {{\boldsymbol{I}}_d} , {{\boldsymbol{\bar \varOmega }}_{{\text{FL}}}} = {{\boldsymbol{\varOmega }}_{{\text{FL}}}} \otimes {{\boldsymbol{I}}_d} , {{\boldsymbol{\bar \varOmega }}_{{\text{FF}}}} = {{\boldsymbol{\varOmega }}_{{\text{FF}}}} \otimes {{\boldsymbol{I}}_d} 。
本文的控制目标是在模型未知和外界干扰条件下,设计一个事件触发机制下的ASV仿射编队机动控制器,从而使该组航行器形成指定的几何队形,且在进行仿射变换的同时保证队形的稳定控制。为此,定义ASV集群系统的期望艏向角为 {{\boldsymbol{\psi }}^*} = {\left( {{\boldsymbol{\psi }}{{_{\text{L}}^*}^{\text{T}}},{\boldsymbol{\psi }}{{_{\text{F}}^*}^{\text{T}}}} \right)^{\text{T}}} ,其中 {\boldsymbol{\psi }}_{\text{L}}^* , {\boldsymbol{\psi }}_{\text{F}}^* 分别为领导者期望艏向角、跟随者期望艏向角的集合;定义ASV集群系统的期望位置为 {p^*} = {\left( {p{{_{\text{L}}^*}^{\text{T}}},p{{_{\text{F}}^*}^{\text{T}}}} \right)^{\text{T}}} ,其中 {\boldsymbol{p}}_{\text{L}}^* , {\boldsymbol{p}}_{\text{F}}^* 分别为领导者期望位置、跟随者期望位置的集合。
假设4:假设领导者由智能控制算法或人为操纵而生成,即 {{\boldsymbol{\psi }}_{\text{L}}} = {\boldsymbol{\psi }}_{\text{L}}^* , {{\boldsymbol{p}}_{\text{L}}} = {\boldsymbol{p}}_{\text{L}}^* 。
由于ASV集群系统内领导者的数量一般较少且已知自身轨迹,故可由智能控制算法或人为操纵生成[19,22-24],因此,假设4合理。
基于假设4,考虑到在不规则水域环境中执行任务时,障碍物可能以多种形式存在,因此,本文将考虑3种典型任务场景,如表1所示,其中:三角阴影表示障碍物,绿色原点表示ASV,黑色实线表示ASV之间构成的边。1)当ASV集群系统在第1种环境中执行任务时,2个中间障碍物的距离较小,如果不进行编队机动,集群可能与障碍物发生碰撞。为了避免碰撞,领导者检测到障碍物时将进行编队缩放机动。2)当在第2种环境中执行任务时,障碍物交错分布,为了避免碰撞,领导者检测到障碍物时将进行编队旋转机动。3)当在第3种环境中执行任务时,2个中间障碍物距离过于狭窄,为了避免碰撞,领导者检测到障碍物时将进行编队剪切机动[17]。
表 1 ASV集群轨迹规划Table 1. Trajectory planning for multiple ASVs障碍物类型 运动描述 一 
二 
三 
2. 控制器设计
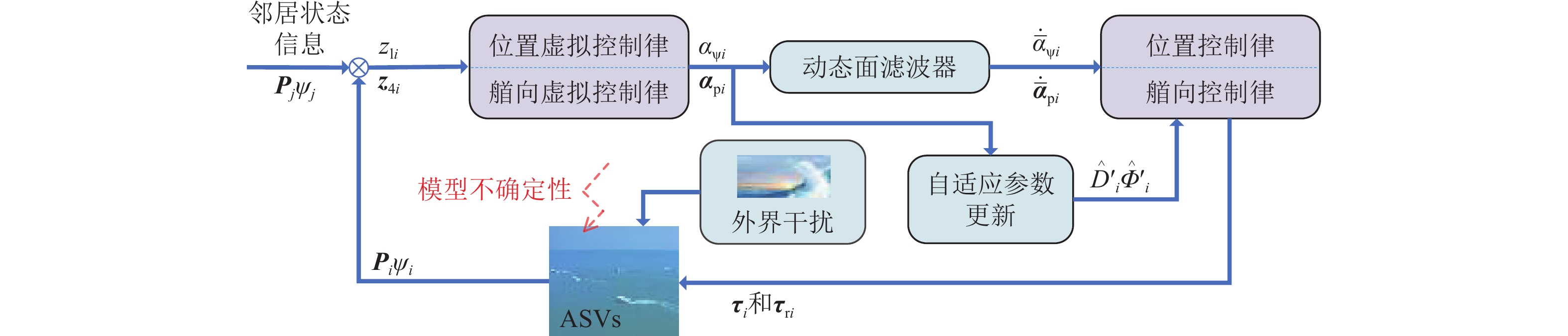
本文为ASV集群系统设计了一种基于局部信息的仿射编队机动控制器,并引入了事件触发以减少航行器之间的信息交换频率,控制流程如图1所示,参数解释详见下文。
2.1 事件触发机制设计
本文提出的事件触发机制用于调节ASV编队的数据交换频率,从而有效节省通信资源。在该机制下,第i艘ASV仅在满足触发条件时,才能通过通信网络将其状态信息发送至所有邻居ASV,以有效避免不必要的通信和更新,从而减少通信负担并提高系统的整体效率。
将第i艘ASV的首次触发时间记为 t_k^i = 0 ,则其时间序列 \left\{ {t_k^i} \right\}_2^\infty 可表示为
\begin{gathered} {{\text{R}}_1}:t_{k + 1}^i = \mathop {{\text{sup}}}\limits_{t > 0} \left\{ {t_k^i{\text{ < }}t\;\;{\text{|}}\begin{array}{*{20}{c}} {\;\;\left\| {{z_{1i}}(t) - {z_{1i}}(t_k^i)} \right\| < {\delta _1}} \\ {{\text{or}}\;\left\| {{r_i}(t) - {r_i}(t_k^i)} \right\| < {\delta _2}} \end{array}} \right\},\forall k \in {\mathbb{N}^ + } \\ {{\text{R}}_2}:t_{k + 1}^i = \mathop {{\text{sup}}}\limits_{t > 0} \left\{ {t_k^i{\text{ < }}t\;{\text{|}}\begin{array}{*{20}{c}} {\;\;\;\left\| {{{\boldsymbol{z}}_{4i}}(t) - {{\boldsymbol{z}}_{4i}}(t_k^i)} \right\| < {\delta _{\text{3}}}} \\ {{\text{or}}\;\left\| {{{\boldsymbol{q}}_i}(t) - {{\boldsymbol{q}}_i}(t_k^i)\;} \right\| < {\delta _{\text{4}}}} \end{array}} \right\},\forall k \in {\mathbb{N}^ + } \end{gathered} (9) 式中: {{\text{R}}_{\text{1}}} 和 {{\text{R}}_{\text{2}}} 分别为触发该组航行器的位置跟踪与方向单位向量一致性跟踪的条件;t为触发时间上界; t_k^i 为第i艘ASV的第k次触发时间,其中k为触发频次, k \in {\mathbb{N}^ + } ,其中 {\mathbb{N}^ + } 为正整数集; {z_{1i}}(t) , {z_{1i}}(t_k^i) 分别为第i艘ASV在t时刻、第k次触发时刻的艏向误差; {{\boldsymbol{z}}_{4i}}(t) , {{\boldsymbol{z}}_{4i}}(t_k^i) 分别为t时刻、第k次触发时刻的相对位置误差; {r_i}(t_k^i) , {{\boldsymbol{q}}_i}(t_k^i) 分别为第k次触发时刻第i艘ASV的艏摇角速度、位置 ; {\delta _\rho }\left( {\rho = 1,2,3,4} \right) 为触发机制的阈值,具体形式为 {\delta _\rho } = \sqrt {{\beta _\rho }^{ - {\eta _\rho }t} + {\beta _{\rho 0}}} ,其中 {\beta _\rho } > 1,0 \leqslant {\eta _\rho } \leqslant 1 , {\beta _{\rho 0}} 为阈值下限。
通过观察式(9)可以发现,由于触发式通信造成的量测误差可以控制在一定阈值范围内,而该阈值与参数 {\delta _\rho } 密切相关,较大的 {\delta _\rho } 意味着触发过程中的ASV容许更大的量测误差,同时还伴随着更低的通信频率和更少的通信资源消耗,但航行器编队过程中的误差变化将更为剧烈。而较小的 {\delta _\rho } 则意味着量测误差需要控制在一个更小的范围内,这将导致更高的通信频率和更大的通信能源消耗。由此可见,设置进行事件触发阈值时,需要进行合理取舍。
2.2 艏向跟踪控制器设计
艏向跟踪一致性的表达式为
\left( {{\boldsymbol{L}} \otimes {{\boldsymbol{I}}_d}} \right){\boldsymbol{\psi }} = {\text{0}} (10) 式中,L为拉普拉斯矩阵,用于描述ASV之间的通信拓扑结构。
为便于控制器设计,定义 {\boldsymbol{\bar L}} = {\boldsymbol{L}} \otimes {{\boldsymbol{I}}_d} ,即
{\boldsymbol{\bar L}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{L}}_{{\text{LL}}}}}&{{{\boldsymbol{L}}_{{\text{LF}}}}} \\ {{{\boldsymbol{L}}_{{\text{FL}}}}}&{{{\boldsymbol{L}}_{{\text{FF}}}}} \end{array}} \right] \otimes {{\boldsymbol{I}}_d} = \left[ {\begin{array}{*{20}{c}} {{{{\boldsymbol{\bar L}}}_{{\text{LL}}}}}&{{{{\boldsymbol{\bar L}}}_{{\text{LF}}}}} \\ {{{{\boldsymbol{\bar L}}}_{{\text{FL}}}}}&{{{{\boldsymbol{\bar L}}}_{{\text{FF}}}}} \end{array}} \right] (11) 式中: {{\boldsymbol{L}}_{{\text{LL}}}} \in {\mathbb{R}^{d{N_{\text{L}}} \times d{N_{\text{L}}}}} , {{\boldsymbol{L}}_{{\text{LF}}}} \in {\mathbb{R}^{d{N_{\text{L}}} \times d{N_{\text{F}}}}} , {{\boldsymbol{L}}_{{\text{FL}}}} \in {\mathbb{R}^{d{N_{\text{F}}} \times d{N_{\text{L}}}}} , {{\boldsymbol{L}}_{{\text{FF}}}} \in {\mathbb{R}^{d{N_{\text{F}}} \times d{N_{\text{F}}}}} ; {{\boldsymbol{\bar L}}_{{\text{LL}}}} = {{\boldsymbol{L}}_{{\text{LL}}}} \otimes {{\boldsymbol{I}}_d} , {{\boldsymbol{\bar L}}_{{\text{LF}}}} = {{\boldsymbol{L}}_{{\text{LF}}}} \otimes {{\boldsymbol{I}}_d} , {{\boldsymbol{\bar L}}_{{\text{FL}}}} = {{\boldsymbol{L}}_{{\text{FL}}}} \otimes {{\boldsymbol{I}}_d} , {{\boldsymbol{\bar L}}_{{\text{FF}}}} = {{\boldsymbol{L}}_{{\text{FF}}}} \otimes {{\boldsymbol{I}}_d} 。
基于假设1,得
{\boldsymbol{\bar L}}\left[ \begin{gathered} {\boldsymbol{\psi }}_{\text{L}}^* \\ {\boldsymbol{\psi }}_{\text{F}}^* \\ \end{gathered} \right] = {\text{0}} \Rightarrow {\boldsymbol{\psi }}_{\text{F}}^* = - {{\boldsymbol{\bar L}}^{ - 1}}_{{\text{FF}}}{{\boldsymbol{\bar L}}_{{\text{FL}}}}{\boldsymbol{\psi }}_{\text{L}}^* (12) 定义第i艘ASV艏向角的跟踪误差为 {{\boldsymbol{e}}_{\psi i}} = {{\boldsymbol{\psi }}_{{\text{F}}i}} - {\boldsymbol{\psi }}_{{\text{F}}i}^*,{\text{ }}i \in {\mathcal{V}_{\text{F}}} ,结合式(12)可得
{{\boldsymbol{e}}_\psi } = {{\boldsymbol{\psi }}_{\text{F}}} + {{\boldsymbol{\bar L}}^{ - 1}}_{{\text{FF}}}{{\boldsymbol{\bar L}}_{{\text{FL}}}}{\boldsymbol{\psi }}_{\text{L}}^* (13) 式中: {{\boldsymbol{\psi }}_{{\text{F}}i}} , {\boldsymbol{\psi }}_{{\text{F}}i}^* 分别为第i艘ASV跟随者艏向角集合与跟随者期望艏向角的集合; {{\boldsymbol{e}}_\psi } 为ASV集群系统艏向角的跟踪误差。
定义第i艘ASV的相对艏向角误差 {z_{1i}} ,以及2个误差变量 {z_{2i}} 和 {z_{3i}} 分别为
\left\{ \begin{aligned} & {z_{1i}} = \sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}\left( {{\psi _i} - {\psi _j}} \right)} ,&& i \in {\mathcal{V}_F} \\ & {z_{2i}} = {{\bar \alpha }_{\psi i}} - {\alpha _{\psi i}},&& i \in {\mathcal{V}_F} \\ & {z_{3i}} = {r_i} - {{\bar \alpha }_{\psi i}},&& i \in {\mathcal{V}_F} \end{aligned} \right. (14) 式中, {\alpha _{\psi i}} 和{\bar \alpha _{\psi i}}分别为所设计的虚拟控制律及经过滤波后的虚拟控制律。
一阶滤波器设计如下:
{\gamma _1}{\dot {\bar \alpha} _{\psi i}} + {\bar \alpha _{\psi i}} = {\alpha _{\psi i}} (15) 式中: {\gamma _1} 为正设计参数; {\dot {\bar \alpha} _{\psi i}} 为滤波后虚拟控制律的导数。令 {\varepsilon _{1i}}(t) = {z_{1i}}(t) - {z_{1i}}(t_k^i) , {\varepsilon _{2i}}(t) = {r_i}(t) - r(t_k^i) 。虚拟控制律作为一阶滤波器的输入,其经过滤波后的虚拟控制律则作为滤波器的输出。
定义误差的集总形式为 {{\boldsymbol{z}}_{1{\text{F}}}} = {\left[ {{z_{11}}, \ldots ,{z_{1i}}, \ldots ,{z_{1{N_{\text{F}}}}}} \right]^{\text{T}}} ,根据式(14)可得:
{{\boldsymbol{\bar L}}^{ - 1}}_{{\text{FF}}}{{\boldsymbol{z}}_{1{\text{F}}}} = {{\boldsymbol{\bar L}}^{ - 1}}_{{\text{FF}}}{{\boldsymbol{\bar L}}_{{\text{FL}}}}{{\boldsymbol{\psi }}_{\text{L}}} + {{\boldsymbol{\psi }}_{\text{F}}} (16) 结合式(16)和式(13)可得 {{\boldsymbol{e}}_\psi } = {{\boldsymbol{\bar L}}^{ - 1}}_{{\text{FF}}}{{\boldsymbol{z}}_{{\text{1F}}}} ,对式(14)求导,得
\begin{split} & {{\dot z}_{1i}} = \sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{z_{3i}}} + \sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{z_{2i}}} + \\ &\quad \sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{\alpha _{\psi i}}} - \sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{r_j}} \end{split} (17) 根据式(17),虚拟控制律为
{\alpha _{\psi i}}\left( t \right) = - \left( {{k_1}{z_{1i}}(t_k^i) - \sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{r_j}(t_k^i)} } \right)/\iota (18) 式中: {k_1} 为正设计参数; \iota = \sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}} 。
将式(18)和 {\varepsilon _{2i}}(t) 代入式(17),得
\begin{split} & {{\dot z}_{1i}} = \sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{z_{3i}}} + \sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{z_{2i}} - } {k_1}{z_{1i}}(t_k^i) - \\&\qquad\qquad \sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{\varepsilon _{2i}}(t)} \end{split} (19) 对{z_{2i}}和{z_{3i}}进行求导,结合式(1),得
\left\{ \begin{aligned} & {{{\dot z}_{2i}} = - \gamma _1^{ - 1}{z_{2i}}} \\ & {{{\dot z}_{3i}} = {f_2}\left( {{u_i},{v_i},{r_i},t} \right) + \tau _i^{\text{r}} + {\tau _{{\text{r}}i}}/{m_{33i}} - {\gamma _1}^{ - 1}{z_{2i}}} \end{aligned}\right. (20) 式中, {f_2}\left( {{u_i},{v_i},{r_i},t} \right) + \tau _i^{\text{r}} 为集总扰动项。利用径向基神经网络对未知函数的在线逼近特性,可将集总扰动项表示为
{f_2}\left( {{u_i},{v_i},{r_i}} \right) + \tau _i^{\text{r}} = {{\boldsymbol{W}}_i}^{*{\text{T}}}{{\boldsymbol{H}}_i}\left( \kappa \right) + {\varepsilon _i}\left( \kappa \right) (21) 式中: {{\boldsymbol{W}}_i}^{*{\text{T}}} 为径向基神经网络权值; {{\boldsymbol{H}}_i}\left( \kappa \right) 为网络隐含层输出,其中 \kappa 为输入参数向量; {\varepsilon _i}\left( \kappa \right) 为网络逼近误差。
为减少逼近过程中的计算复杂性,结合最小参数学习法,可将式(21)进一步表示为
\left\| {{f_2}\left( {{u_i},{v_i},{r_i}} \right) + \tau _i^{\text{r}}} \right\| \leqslant {\varPhi _i}{\chi _i} + {D_i} (22) 式中, {\varPhi _i} = \left\| {{{\boldsymbol{W}}_i}^{*{\text{T}}}} \right\| , {\chi _i} = \left\| {{{\boldsymbol{H}}_i}\left( \kappa \right)} \right\| , {D_i} = \left\| {{\varepsilon _i}\left( \kappa \right)} \right\| 。
根据式(20),所设计的控制律如下:
{\tau _{{\text{r}}i}}\left( t \right) = {m_{33i}}\left( - {\hat \varPhi _i}{\chi _i}\left( \kappa \right) - {\hat D_i} - \sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{z_{1i}}(t_k^i)} - {k_2}{z_{3i}}(t_k^i)\right) (23) 式中: {\hat \varPhi _i} 为 {\varPhi _i} 的估计; {\hat D_i} 为 {D_i} 的估计; {z_{1i}}(t_k^i) 为 t_k^i 时刻的相对艏向角误差; {k_2} 为正设计参数; {z_{3i}}(t_k^i) 为 t_k^i 时刻的误差变量。
所设计的自适应律 {\dot {\hat D}_i} , {\dot {\hat \varPhi} _i} 如下:
\left\{ \begin{aligned} & {{{\dot {\hat D}}_i} = \left\| {{z_{3i}}(t_k^i)} \right\| - {c_1}{{\hat D}_i}} \\& {{{\dot {\hat \varPhi} }_i} = \left\| {{z_{3i}}(t_k^i)} \right\|\left\| {{\chi _i}} \right\| - {c_2}{{\hat \varPhi }_i}} \end{aligned}\right. (24) 式中, {c_1} 和 {c_2} 为正设计参数。定义误差项分别为 {\tilde D_i} = {D_i} - {\hat D_i} 和 {\tilde \varPhi _i} = {\hat \varPhi _i} - {\varPhi _i} 。
定理1 对于ASV编队系统,在事件触发机制下,利用虚拟控制律式(18)和控制律式(23)、式(24),系统艏向角误差将全局渐近稳定。
证明:选取Lyapunov候选函数 {V_1} :
{V_1} = \sum\nolimits_{j \in {\mathcal{N}_i}} {\left( {\frac{1}{2}z_{1i}^{\text{2}} + \frac{1}{2}z_{2i}^2 + \frac{1}{2}z_{3i}^2 + \frac{1}{2}\tilde D_i^2 + \frac{1}{2}\tilde \varPhi _i^2} \right)} (25) 对 {V_1} 求导,得
\begin{gathered} {{\dot V}_1} = \sum\nolimits_{j \in {\mathcal{N}_i}} \Bigg({z_{3i}}\sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{\varepsilon _{1i}}} + {k_1}{z_{1i}}{\varepsilon _{1i}} - \\ {z_{1i}}\sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{\varepsilon _{2i}}} - {\gamma ^{ - 1}}{z_{2i}}{z_{2i}} - {k_2}{z_{3i}}{z_{3i}} - \\ {k_1}z_{1i}^{\text{2}} + {z_{1i}}\sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{z_{2i}}} + {z_{3i}}{\gamma _1}^{ - 1}{z_{2i}} + {k_2}{z_{3i}}{\varepsilon _{2i}}\Bigg) -\\ {c_1}{{\tilde D}_i}{{\hat D}_i} - {c_2}{{\tilde \varPhi }_i}{{\hat \varPhi }_i} \\ \end{gathered} (26) 根据文献[25]可知,恒存在矩阵{{\boldsymbol{Q}}_1}和{{\boldsymbol{Q}}_2},使得 \sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}} = {{\boldsymbol{Q}}_1}^{\text{T}}{{\boldsymbol{Q}}_2} ,因此式(26)可以改写为
{{\dot V}_1} = - \sum\nolimits_{j \in {\mathcal{N}_i}} {\left( {{k_1}z_{1i}^{\text{2}} + {\gamma _1}^{ - 1}z_{2i}^2 + {k_2}z_{3i}^2} \right)} - {c_2}{{\tilde \varPhi }_i}{{\hat \varPhi }_i} + \begin{gathered} \sum\nolimits_{j \in {\mathcal{N}_i}} {\frac{1}{2}\left( {z_{2i}^2 + z_{3i}^2} \right)} + \frac{1}{2}\Bigg(\frac{1}{{{\omega _1}}}z_{1i}^{\text{2}}{{\boldsymbol{Q}}_1}^{\text{T}}{{\boldsymbol{Q}}_1} + \\ {\omega _1}z_{2i}^{\text{2}}{{\boldsymbol{Q}}_2}^{\text{T}}{{\boldsymbol{Q}}_2}\Bigg) + \sum\nolimits_{j \in {\mathcal{N}_i}} \Bigg({z_{3i}}\sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{\varepsilon _{1i}}} - \\ {z_{1i}}\sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{\varepsilon _{2i}}} + {k_1}{z_{1i}}{\varepsilon _{1i}} + {k_2}{z_{3i}}{\varepsilon _{2i}}\Bigg) - {c_1}{{\tilde D}_i}{{\hat D}_i} \\ \end{gathered} (27) 式中: {\omega _1} 为常数大于0; {z_{2i}} 为误差变量。
设定 {\lambda _{\min }} 为取最小值,如果满足 {\lambda _{\min }}( {{{{{\boldsymbol{Q}}_1}^{\text{T}}{{\boldsymbol{Q}}_1}} / {2{\omega _1}}}} ) > - {k_1} , {k_2} > {1 / 2} , {\gamma _1}^{ - 1} > \dfrac{1}{2} + {\lambda _{\min }}( {{\omega _1}{{\boldsymbol{Q}}_2}^{\text{T}}{{\boldsymbol{Q}}_2}} ) ,则式(27)可改写为
{\dot V_1} \leqslant - {\rho _1}{V_1} + {\Delta _1} (28) 其中
\begin{gathered} {\rho _1} = 2\min \Bigg(\Bigg({k_1} + {\lambda _{\min }}\Bigg(\frac{1}{{2{\omega _1}}}{{\boldsymbol{Q}}_1}^{\text{T}}{{\boldsymbol{Q}}_1}\Bigg)\Bigg),{c_1},{c_2}, \\ \Bigg({k_2} - \frac{1}{2}\Bigg),({\gamma _1}^{ - 1} - \frac{1}{2}{\lambda _{\min }}({\omega _1}{{\boldsymbol{Q}}_2}^{\text{T}}{{\boldsymbol{Q}}_2}))\Bigg) \\ {\Delta _1} = \sum\nolimits_{j \in {\mathcal{N}_i}} {\Bigg({z_{3i}}\sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{\varepsilon _{1i}}} } + {k_2}{z_{3i}}{\varepsilon _{2i}} - \\ {z_{1i}}\sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{\varepsilon _{2i}}(t)} + {k_1}{z_{1i}}{\varepsilon _{1i}}\Bigg) \\ \end{gathered} (29) 由此可得,在水平面航行的一组ASV编队的艏向跟踪误差是全局渐近稳定的,其收敛区域为 \sqrt {{{2{\Delta _1}}/ {{\rho _1}}}} 。根据式(28)可以看出,适当增大控制参数 {k_1} , {k_2} , {c_1} , {c_2} ,将加快系统误差的收敛速度,但会加剧抖振现象,因此,选择控制参数时应在精度与减少抖振之间进行权衡,从而获得最佳性能。
2.3 位置跟踪控制器设计
根据应力矩阵的性质,得
{\boldsymbol{\bar \varOmega }}\left[ \begin{gathered} {\boldsymbol{p}}_{\text{L}}^* \\ {\boldsymbol{p}}_{\text{F}}^* \\ \end{gathered} \right] = {\text{0}} \Rightarrow {\boldsymbol{p}}_{\text{F}}^* = - {{\boldsymbol{\bar \varOmega }}^{ - 1}}_{{\text{FF}}}{{\boldsymbol{\bar \varOmega }}_{{\text{FL}}}}{\boldsymbol{p}}_{\text{L}}^* (30) 定义第i艘ASV的位置跟踪误差为 {e_{{\text{p}}i}} = {{\boldsymbol{p}}_{{\text{F}}i}} - {\boldsymbol{p}}_{{\text{F}}i}^*, i \in {\mathcal{V}_{\text{F}}} ,其编队集总形式为 {e_{\text{p}}} = {{\boldsymbol{p}}_{\text{F}}} - {\boldsymbol{p}}_{\text{F}}^* 。结合式(30)可得 {e_{\text{p}}} = {{\boldsymbol{p}}_{\text{F}}} + {{\boldsymbol{\bar \varOmega }}^{ - 1}}_{{\text{FF}}}{{\boldsymbol{\bar \varOmega }}_{{\text{FL}}}}{\boldsymbol{p}}_{\text{L}}^* 。
定义第i艘ASV的相对位置误差为 {z_{4i}} ,以及2个误差变量为 {z_{5i}} 和 {z_{6i}} :
\left\{ \begin{aligned} & {{\boldsymbol{z}}_{4i}} = \sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}\left( {{{\boldsymbol{p}}_i} - {{\boldsymbol{p}}_j}} \right)} ,&& i \in {\mathcal{V}_{\text{F}}} \\ & {{\boldsymbol{z}}_{5i}} = {{\bar {\boldsymbol{\alpha}} }_{{\text{p}}i}} - {{\boldsymbol{\alpha}} _{{\text{p}}i}},&& i \in {\mathcal{V}_{\text{F}}} \\ & {{\boldsymbol{z}}_{6i}} = {{\boldsymbol{q}}_i} - {{\bar {\boldsymbol{\alpha}} }_{{\text{p}}i}},&& i \in {\mathcal{V}_{\text{F}}} \end{aligned}\right. (31) 式中: {w_{ij}} 为边 \left( {i,j} \right) 的权重值;{{\boldsymbol{\alpha}} _{{\text{p}}i}}和 {\bar {\boldsymbol{\alpha }}_{{\text{p}}i}} 分别为拟设计的虚拟控制律以及滤波后的虚拟控制律。
一阶滤波器设计如下:
{\gamma _2}{\dot {\bar {\boldsymbol{\alpha}}} _{{\text{p}}i}} + {\bar {\boldsymbol{\alpha}} _{{\text{p}}i}} = {{\boldsymbol{\alpha}} _{{\text{p}}i}} (32) 式中: {\gamma _2} 为正设计参数; {\dot {\bar {\boldsymbol{\alpha}}} _{{\text{p}}i}} 为滤波后虚拟控制律 {\bar {\boldsymbol{\alpha}} _{{\text{p}}i}} 的导数。
令 {{\boldsymbol{\varepsilon }}_{3i}}(t) = {z_{4i}}(t_s^i) - {{\boldsymbol{z}}_{4i}}(t_k^i) , {{\boldsymbol{\varepsilon }}_{4i}}(t) = {{\boldsymbol{q}}_i}(t_s^i) - {{\boldsymbol{q}}_i}(t_k^i) ,其中 t_s^i 为第s次触发时刻。定义误差向量集总形式为 {z_{{\text{4F}}}} = {\left[ {z_{41}^{\text{T}}, \ldots ,z_{4i}^{\text{T}}, \ldots ,z_{4{N_{\text{F}}}}^{\text{T}}} \right]^{\text{T}}} ,根据式(31)可得
{{\boldsymbol{z}}_{4{\text{F}}}} = {{{\boldsymbol{\bar \varOmega }}}_{{\text{FF}}}}{{\boldsymbol{p}}_{\text{F}}} + {{{\boldsymbol{\bar \varOmega }}}_{{\text{FL}}}}{{\boldsymbol{p}}_{\text{L}}} \Rightarrow {{\boldsymbol{p}}_{\text{F}}} + {{{\boldsymbol{\bar \varOmega }}}^{ - 1}}_{{\text{FF}}}{{{\boldsymbol{\bar \varOmega }}}_{{\text{FL}}}}{\boldsymbol{p}}_{\text{L}}^* = {{{\boldsymbol{\bar \varOmega }}}^{ - 1}}_{{\text{FF}}}{z_{4{\text{F}}}} (33) 结合式(30)和式(33)可得 {e_{\text{p}}} = {{\boldsymbol{\bar \varOmega }}^{ - 1}}{z_{4{\text{F}}}} ,因此,对 {z_{4i}} 求导,得
\begin{gathered} {{\dot z}_{4i}} = \sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}{z_{5i}}} + \sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}{z_{6i}}} + \\ \sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}{\alpha _{{\text{p}}i}}} - \sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}{{\boldsymbol{q}}_j}} \\ \end{gathered} (34) 根据式(34),设计如下的虚拟控制律:
{\alpha _{{\text{p}}i}}\left( t \right) = - {\left( {\sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}} } \right)^{ - 1}}({k_3}{z_{4i}}(t_k^i) - \sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}{{\boldsymbol{q}}_j}(t_k^i)} ) (35) 式中, {k_3} 为正设计参数。
将式(35)代入式(34),得
{\dot z_{4i}} = \sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}{z_{5i}}} + \sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}{z_{6i}}} - {k_3}{z_{4i}} (36) 对 {z_{5i}} 和 {z_{6i}} 分别求导,再结合式(1),得
\begin{gathered} {{\dot z}_{5i}} = {{\dot {\bar \alpha} }_{{\text{p}}i}} - {{\dot \alpha }_{{\text{p}}i}} = - \gamma _2^{ - 1}{z_{5i}} \\ {{\dot z}_{6i}} = {{\dot q}_i} - {{\dot {\bar \alpha} }_{{\text{p}}i}} = {f_1}\left( {{u_i},{v_i},{r_i}} \right) + \tau _i^{\text{d}} + {\hbar _i}{{\boldsymbol{\tau }}_i} - {{\dot {\bar \alpha} }_{{\text{p}}i}} \\ \end{gathered} (37) 式中, {f_1}\left( {{u_i},{v_i},{r_i}} \right) + \tau _i^{\text{d}} 为集总扰动项,参考第2.2节,结合最小参数学习法和径向基神经网络,得
\begin{gathered} \left\| {{f_1}\left( {{u_i},{v_i},{r_i}} \right) + {\boldsymbol{\tau }}_i^{\text{d}}} \right\| \leqslant \\ \left\| {{\boldsymbol{W}}{'_i}^{{\text{*T}}}} \right\|\left\| {{\boldsymbol{H}}{'_i}\left( \kappa \right)} \right\| + \left\| {{\boldsymbol{\varepsilon }}{'_i}\left( \kappa \right)} \right\| \leqslant \varPhi {'_i}\chi {'_i} + D{'_i} \\ \end{gathered} (38) 式中: \varPhi {'_i} = \left\| {{\boldsymbol{W}}{'_i}^{*{\text{T}}}} \right\| ,表示径向基神经网络权值; \chi {'_i} = \left\| {{\boldsymbol{H}}{'_i}\left( \kappa \right)} \right\| ,表示网络隐含层输出; D{'_i} = \left\| {{\boldsymbol{\varepsilon }}{'_i}\left( \kappa \right)} \right\| ,表示网络逼近误差。
根据式(37),所设计的控制律 {\hbar _i}{{\boldsymbol{\tau }}_i} 如下:
{\hbar _i}{{\boldsymbol{\tau }}_i} = - \hat \varPhi {'_i}\chi {'_i}\left( \kappa \right) - \hat D{'_i} - \sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}{z_{4i}} - {k_4}{z_{6i}}} (39) 式中: \chi {'_i} 为网络隐含层输出; {k_4} 为正设计参数。
所设计的自适应律 \dot {\hat D}{'_i} , \dot {\hat \varPhi} {'_i} 如下:
\left\{ \begin{aligned} & {\dot {\hat D}{'_i} = \left\| {{{\boldsymbol{z}}_{5i}}(t_k^i)} \right\| - {c_3}\hat D{'_i}} \\ & {\dot {\hat \varPhi} {'_i} = \left\| {{{\boldsymbol{z}}_{5i}}(t_k^i)} \right\|\left\| {\chi {'_i}} \right\| - {c_4}\hat \varPhi {'_i}} \end{aligned} \right. (40) 式中: {{\boldsymbol{z}}_{5i}}(t_k^i) 为 t_k^i 时刻的位置误差; {c_3} 和 {c_4} 为正设计参数。定义误差项 \tilde D{'_i} = D{'_i} - \hat D{'_i} 和 \tilde \varPhi {'_i} = \hat \varPhi {'_i} - \varPhi {'_i} 。
定理2 对于ASV编队系统,在事件触发机制下,利用虚拟控制律式(35)和控制律式(39)、式(40),系统位置误差是全局渐近稳定的。
证明:选取Lyapunov候选函数 {V_2} :
{V_2} = \sum\nolimits_{j \in {\mathcal{N}_i}} {\left( {\frac{1}{2}z_{4i}^{\text{T}}{z_{4i}} + \frac{1}{2}z_{5i}^{\text{T}}{z_{5i}} + \frac{1}{2}z_{6i}^{\text{T}}{z_{6i}} + \frac{1}{2}\tilde D_i^{\prime 2} + \frac{1}{2}\tilde \varPhi _i^{\prime 2}} \right)} (41) 对 {V_2} 求导,得
\begin{gathered} {{\dot V}_2} = \sum\nolimits_{j \in {\mathcal{N}_i}} \Bigg(z_{6i}^{\text{T}}\sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}{{\boldsymbol{\varepsilon }}_{3i}}} - z_{5i}^{\text{T}}\gamma _2^{ - 1}{z_{5i}} - \\ z_{4i}^{\text{T}}\sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}{{\boldsymbol{\varepsilon }}_{4i}}} + {k_3}z_{4i}^{\text{T}}{{\boldsymbol{\varepsilon }}_{3i}} - {k_3}z_{4i}^{\text{T}}{z_{4i}} - \\ {k_4}z_{6i}^{\text{T}}{z_{6i}} + z_{6i}^{\text{T}}\gamma _2^{ - 1}{z_{5i}} + z_{4i}^{\text{T}}\sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}{z_{5i}}} + \\ {k_4}{z_{6i}}{{\boldsymbol{\varepsilon }}_{4i}}\Bigg) - {c_3}\tilde D{'_i}\hat D{'_i} - {c_4}\tilde \varPhi {'_i}\hat \varPhi {'_i} \\ \end{gathered} (42) 参照上文式(27)的处理过程,对于参数项 \sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}} ,恒存在矩阵{{\boldsymbol{Q}}_3}和{{\boldsymbol{Q}}_4},使得 \sum\nolimits_{j \in {\mathcal{N}_i}} {{w_{ij}}} = {{\boldsymbol{Q}}_3}^{\text{T}}{{\boldsymbol{Q}}_4} 。设定 {\omega _2} 为正常数,若满足条件 {\lambda _{\min }}( {{{{{\boldsymbol{Q}}_3}^{\text{T}}{{\boldsymbol{Q}}_3}} / {2{\omega _2}}}} ) > - {k_3} , {k_4} > {1 /2} , {\gamma _2}^{ - 1} > \dfrac{1}{2} + {\lambda _{\min }}( {{\omega _1}{{\boldsymbol{Q}}_4}^{\text{T}}{{\boldsymbol{Q}}_4}} ) ,则式(42)可进一步简化为
{\dot V_2} \leqslant - {\rho _2}{V_2} + {\Delta _2} (43) 其中
\begin{split} & {\rho }_{2}=2\mathrm{min}(\left({k}_{3}+{\lambda }_{\mathrm{min}}\left({Q}_{3}{}^{\text{T}}{Q}_{3}/2{\omega }_{2}\right)\right)\text{,}\left({k}_{4}-1/2\right),\\&\quad\quad \left({\gamma }_{2}{}^{-1}-1/2-{\lambda }_{\mathrm{min}}\left({\omega }_{2}{Q}_{4}{}^{\text{T}}{Q}_{4}\right)\right),{c}_{3},{c}_{4})\\&\quad\quad {\Delta }_{2} ={\displaystyle {\sum }_{j\in {\mathcal{N}}_{i}}\Bigg({\boldsymbol{z}}_{6i}^{\text{T}}{\displaystyle {\sum }_{j\in {\mathcal{N}}_{i}}{w}_{ij}{\varepsilon }_{3i}}}+{k}_{4}{\boldsymbol{z}}_{6i}{\varepsilon }_{4i}-\\&\quad\quad\quad\quad {\boldsymbol{z}}_{4i}^{\text{T}}{\displaystyle {\sum }_{j\in {\mathcal{N}}_{i}}{w}_{ij}{\varepsilon }_{4i}}+{k}_{3}{\boldsymbol{z}}_{4i}^{\text{T}}{\varepsilon }_{3i}\Bigg) \end{split} (44) 由此可见,该ASV编队在水平面航行时的位置跟踪误差是全局渐近稳定的,其收敛区域为 \sqrt {{{2{\Delta _2}} \mathord{\left/ {\vphantom {{2{\Delta _2}} {{\rho _2}}}} \right. } {{\rho _2}}}} 。根据式(43)可以看出,适当增大控制参数 {k_3} , {k_4} , {c_3} , {c_4} ,将加快位置跟踪误差的收敛速度,但会加剧抖振现象,因此,选择控制参数时应在精度与减少抖振之间进行权衡,从而获得最佳性能。
2.4 Zeno行为分析
如果在有限时间内触发无限次的事件触发机制,则称为Zeno行为,本节将证明ASV组成的编队系统不存在Zeno行为。
对 {\varepsilon _{1i}}(t) 求导并结合式(19),得
\begin{gathered} {{\dot \varepsilon }_{1i}}(t) = {{\dot z}_{1i}} = \sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{z_{3i}}} + \sum\nolimits_{j \in {\mathcal{N}_i}} {{a_{ij}}{z_{2i}}} - {k_1}{z_{1i}} \leqslant \\ \sum\nolimits_{j \in {\mathcal{N}_i}} {\left\| {{a_{ij}}{z_{3i}}} \right\|} + \sum\nolimits_{j \in {\mathcal{N}_i}} {\left\| {{a_{ij}}{z_{2i}}} \right\|} + {k_1}\left\| {{z_{1i}}} \right\| : = {\varphi _1} \end{gathered} (45) 式中, : = 为定义符号,表示将整个不等式上界定义为常数 {\varphi _1} 。
式(45)的解为
{\varepsilon _{1i}}(t) = \int_{t_k^i}^t {{\varphi _1}} {\text{d}}\ell = {\varphi _1}\left( {t - t_k^i} \right) (46) 式中: {\varphi _1} 为有界正常数; \ell 为积分变量。 因为式(14)、式(29)、式(44)中 \left\| {{a_{ij}}{z_{3i}}} \right\| , \left\| {{a_{ij}}{z_{2i}}} \right\| , \left\| {{z_{1i}}} \right\| 均是有界的,所以函数 {\varepsilon _{1i}}(t) 是严格单调递增有界的,当且仅当 t = t_k^i 时, {\varepsilon _{1i}}(t) = 0 。
对于式(9)的事件触发机制,在事件触发的所有时间间隔内,该组ASV编队相对状态的测量信号 {z_{1i}}(t_k^i) 及其执行器所接收的信号 {\tau _{{\text{r}}i}}(t_k^i) 均保持不变。 {\delta _\rho } = \sqrt {{\beta _\rho }^{ - {\eta _\rho }t} + {\beta _{\rho 0}}} 作为该触发机制的阈值函数,是严格单调递减的。当 {\varepsilon _{1i}}(t) = \sqrt {{\beta _1}^{ - {\eta _1}t} + {\beta _{10}}} 时,即可生成下一时刻的采样结果,定义事件触发机制的时间间隔下限为 {\bar T_1} ,结合 \sqrt {{\beta _{10}}} \leqslant {\varphi _1}\left( {t - t_k^i} \right) ,得
{\bar T_1} \geqslant {{\sqrt {{\beta _{10}}} } \mathord{\left/ {\vphantom {{\sqrt {{\beta _{10}}} } {{\varphi _1}}}} \right. } {{\varphi _1}}} (47) 同理,对于其他3种触发机制,可知最小事件触发间隔为
{\overline{T}}_{i}\ge \sqrt{{\beta }_{\rho 0}}/{\phi }_{i},其中\rho =2,3,4 (48) 综上所述,该组ASV编队中存在最小事件触发间隔 {\bar T_i} ,所以上述阈值的设计是合理的。同时,通过增加 {\beta _{\rho 0}} 可以增加触发时间间隔,从而节省通信资源。然而,ASV编队在不频繁更新控制信号与测量信号的情况下,可能会在一定程度上增加跟踪误差。因此,在设计过程中必须考虑通信资源与控制精度之间的平衡,以确保航行器编队的性能符合各方需求。
3. 仿真结果
ASV模型参数[26]如表2所示,ASV编队的初始条件如表3所示,一组7艘ASV,包括4艘领导ASV和3辆跟随ASV。为验证本文提出的跟随者协同控制方法的有效性,可将领导者的位置直接设置为期望位置,以满足 {{\boldsymbol{\psi }}_{\text{L}}} = {\boldsymbol{\psi }}_{\text{L}}^* , {{\boldsymbol{p}}_{\text{L}}} = {\boldsymbol{p}}_{\text{L}}^* 。表4所示为航行器编队控制器的有关参数。
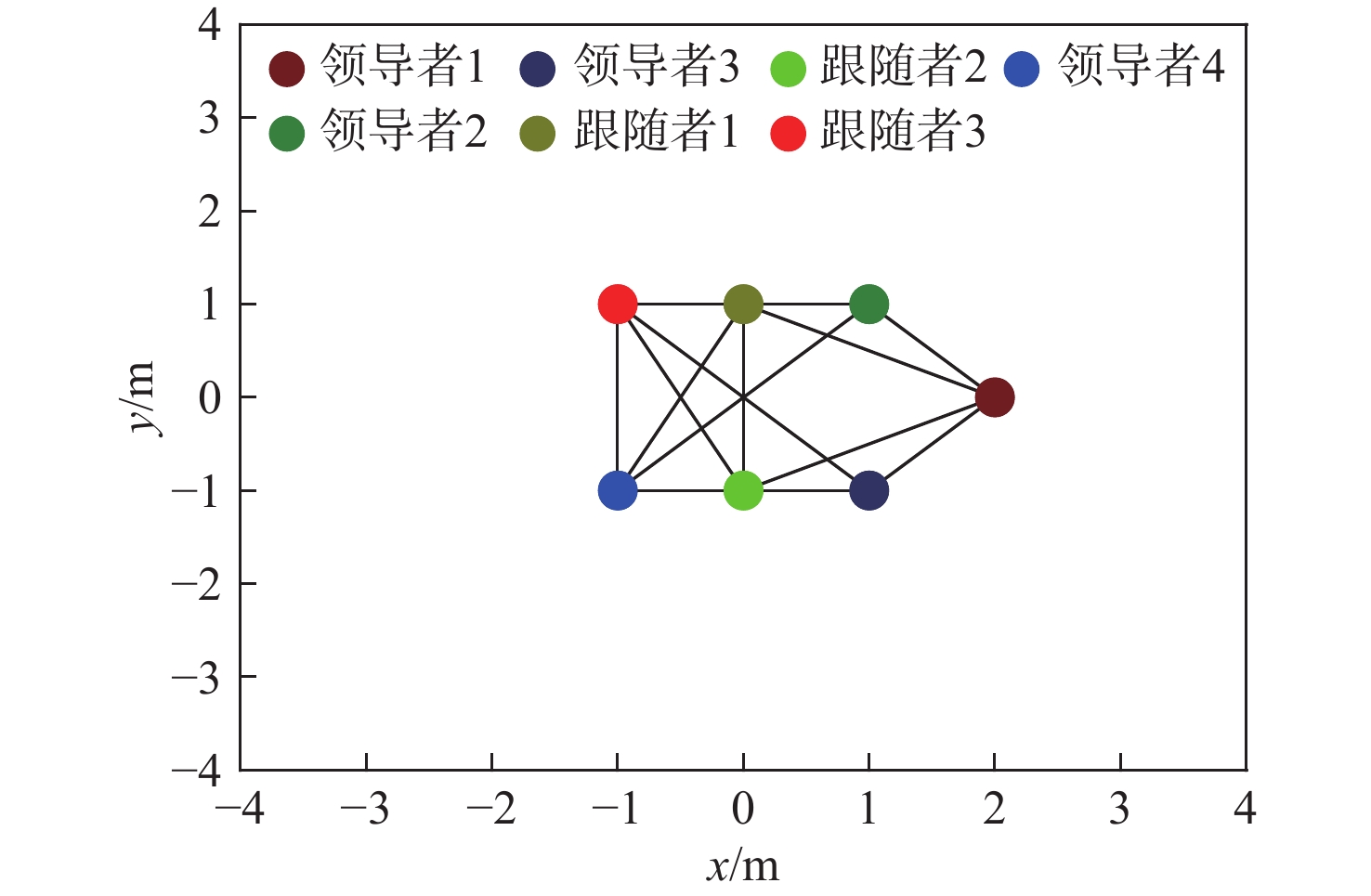
表 2 ASV的模型参数Table 2. The model parameters of ASV参数名称 数值 惯性质量/ kg {m_{11}} = 25.8 , {m_{22}} = 33.8 , {m_{33}} = 2.76 水动力阻尼系数 {d_{11}} = 2 , {d_{22}} = 7 , {d_{33}} = 0.5 表 3 ASV编队的初始状态Table 3. The initial states of the ASV formationASV编号 数值 ASV1 {\left[{x}_{1},{y}_{1},{\psi }_{1}\right]}^{\text{T}}={\left[0.2,2,1.57\right]}^{\text{T}},{\left[{u}_{1},{v}_{1},{r}_{1}\right]}^{\text{T}}={\left[0,0,0\right]}^{\text{T}} ASV2 {\left[{x}_{2},{y}_{2},{\psi }_{2}\right]}^{\text{T}}={\left[-1,1,1.7\right]}^{\text{T}},{\left[{u}_{2},{v}_{2},{r}_{2}\right]}^{\text{T}}={\left[0,0,0\right]}^{\text{T}} ASV3 {\left[{x}_{3},{y}_{3},{\psi }_{3}\right]}^{\text{T}}={\left[1,1,1.48\right]}^{\text{T}},{\left[{u}_{3},{v}_{3},{r}_{3}\right]}^{\text{T}}={\left[0,0,0\right]}^{\text{T}} ASV4 {\left[{x}_{4},{y}_{4},{\psi }_{4}\right]}^{\text{T}}={\left[1.8,-1.8,1.6\right]}^{\text{T}},{\left[{u}_{4},{v}_{4},{r}_{4}\right]}^{\text{T}}={\left[0,0,0\right]}^{\text{T}} ASV5 {\left[{x}_{5},{y}_{5},{\psi }_{5}\right]}^{\text{T}}={\left[-2.5,-0.5,1.6\right]}^{\text{T}},{\left[{u}_{5},{v}_{5},{r}_{5}\right]}^{\text{T}}={\left[0,0,0\right]}^{\text{T}} ASV6 {\left[{x}_{6},{y}_{6},{\psi }_{6}\right]}^{\text{T}}={\left[1.1,1.2,1.6\right]}^{\text{T}},{\left[{u}_{6},{v}_{6},{r}_{6}\right]}^{\text{T}}={\left[0,0,0\right]}^{\text{T}} ASV7 {\left[{x}_{7},{y}_{7},{\psi }_{7}\right]}^{\text{T}}={\left[1,-1,1.5\right]}^{\text{T}},{\left[{u}_{7},{v}_{7},{r}_{7}\right]}^{\text{T}}={\left[0,0,0\right]}^{\text{T}} 表 4 控制方法的设计参数Table 4. Designed parameters of control method参数名称 数值 控制器参数 {k_1} = 17 , {k_2} = 0.14 , {k_3} = 17 , {k_4} = 0.14 , {c_1} = {c_2} = {c_3} = {c_4} = 0.1 一阶滤波器参数 {\gamma _1} = 100 , {\gamma _2} = 100 事件触发机制参数 {\beta _\rho } = 2 , {\beta _{\rho 0}} = 0.0001 , {\eta _\rho } = 0.2 图2所示为ASV编队的通信拓扑图,其中R为ASV编队的标称构型,L为拉普拉斯矩阵, {\boldsymbol{\varOmega }} 为无向图 \mathcal{G} 的应力矩阵:
{\boldsymbol{R}} = {\left[ {\begin{array}{*{20}{c}} 2&1&1&0&0&{ - 1}&{ - 1} \\ 0&1&{ - 1}&1&{ - 1}&1&{ - 1} \end{array}} \right]^{\text{T}}} (49) {\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} 4&{ - 1}&{ - 1}&{ - 1}&{ - 1}&0&0 \\ { - 1}&3&0&{ - 1}&0&0&{ - 1} \\ { - 1}&0&3&0&{ - 1}&{ - 1}&0 \\ { - 1}&{ - 1}&0&5&{ - 1}&{ - 1}&{ - 1} \\ { - 1}&0&{ - 1}&{ - 1}&5&{ - 1}&{ - 1} \\ 0&0&{ - 1}&{ - 1}&{ - 1}&4&{ - 1} \\ 0&{ - 1}&0&{ - 1}&{ - 1}&{ - 1}&4 \end{array}} \right] (50) {\boldsymbol{\varOmega }} = \left[ \begin{matrix} {{{0}}{{.405\;2}}}&{{{ - 0}}{{.405\;2}}}&{{{ - 0}}{{.405\;2}}}&{{{0}}{{.202\;6}}}&{{{0}}{{.202\;6}}}&{{0}}&{{0}} \\ {{{ - 0}}{{.405\;2}}}&{{{1}}{{.013\;0}}}&{{0}}&{{{ - 0}}{{.810\;4}}}&{{0}}&{{0}}&{{{0}}{{.202\;6}}} \\ {{{ - 0}}{{.405\;2}}}&{{0}}&{{{1}}{{.013\;0}}}&{{0}}&{{{ - 0}}{{.810\;4}}}&{{{0}}{{.202\;6}}}&{{0}} \\ {{{0}}{{.202\;6}}}&{{{ - 0}}{{.810\;4}}}&{{0}}&{{{1}}{{.246\;5}}}&{{{ - 0}}{{.233\;5}}}&{{{ - 0}}{{.537\;4}}}&{{{0}}{{.132\;1}}} \\ {{{0}}{{.202\;6}}}&{{0}}&{{{ - 0}}{{.810\;4}}}&{{{ - 0}}{{.233\;5}}}&{{{1}}{{.246\;5}}}&{{{0}}{{.132\;1}}}&{{{ - 0}}{{.537\;4}}} \\ {{0}}&{{0}}&{{{0}}{{.202\;6}}}&{{{ - 0}}{{.537\;4}}}&{{{0}}{{.132\;1}}}&{{{ - 0}}{{.537\;4}}}&{{{ - 0}}{{.334\;8}}} \\ {{0}}&{{{0}}{{.202\;6}}}&{{0}}&{{{0}}{{.132\;1}}}&{{{ - 0}}{{.537\;4}}}&{{{ - 0}}{{.334\;8}}}&{{{0}}{{.537\;4}}} \end{matrix} \right] (51) 将外界干扰设置为
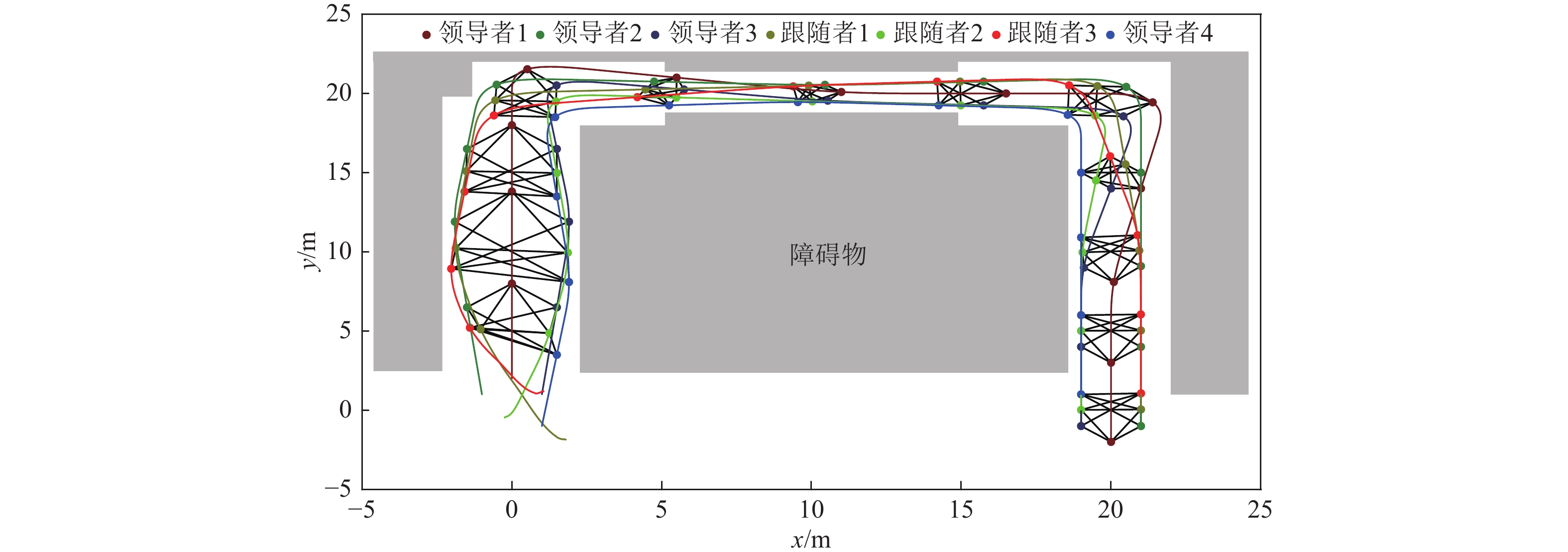
\left[ {\begin{array}{*{20}{c}} {\tau _i^{\text{u}}} \\ {\tau _i^{\text{v}}} \\ {\tau _i^{\text{r}}} \end{array}} \right] = \left[ \begin{gathered} - 0.2\cos (0.5t)\cos (t) \\ 0.01\sin (0.1t) \\ 0.06\sin (1.1t)\cos (0.3t) \\ \end{gathered} \right] (52) 图3~图6展示了ASV编队在时间变化过程中的仿真结果。图3所示为该组ASV编队在水平面中的轨迹图,可见本文所设计的控制器充分利用了仿射变换,实现了良好的跟踪能力。
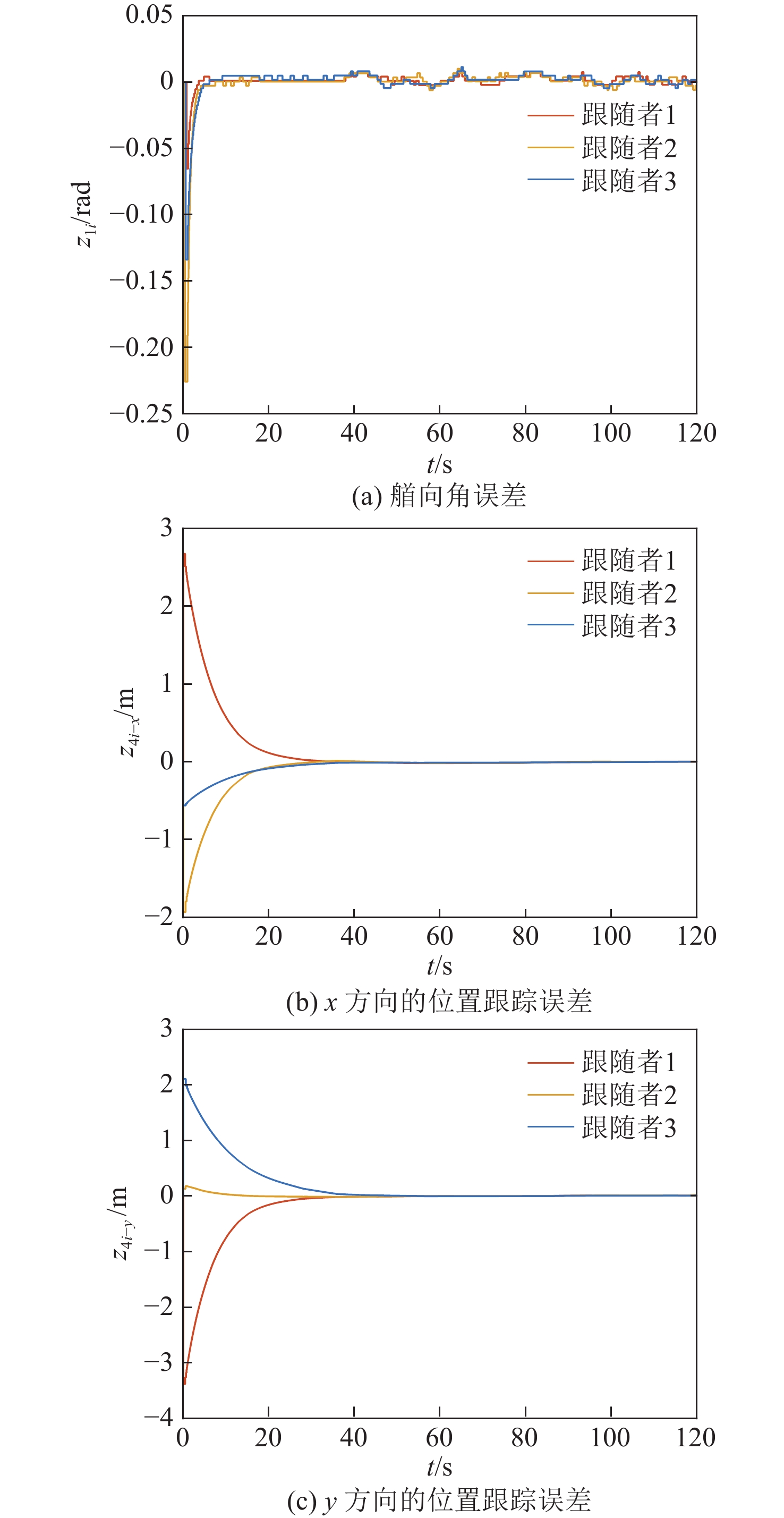
图4展示了3艘ASV的艏向角误差和相对位置误差,可以看出,在上述控制律的作用下,编队的跟踪控制在大约33 s后达到了稳定阶段,此时ASV的姿态角跟踪误差小于0.02,相对位置跟踪误差小于0.015。对于普通的跟踪控制任务而言,该控制精度可以满足任务需求。
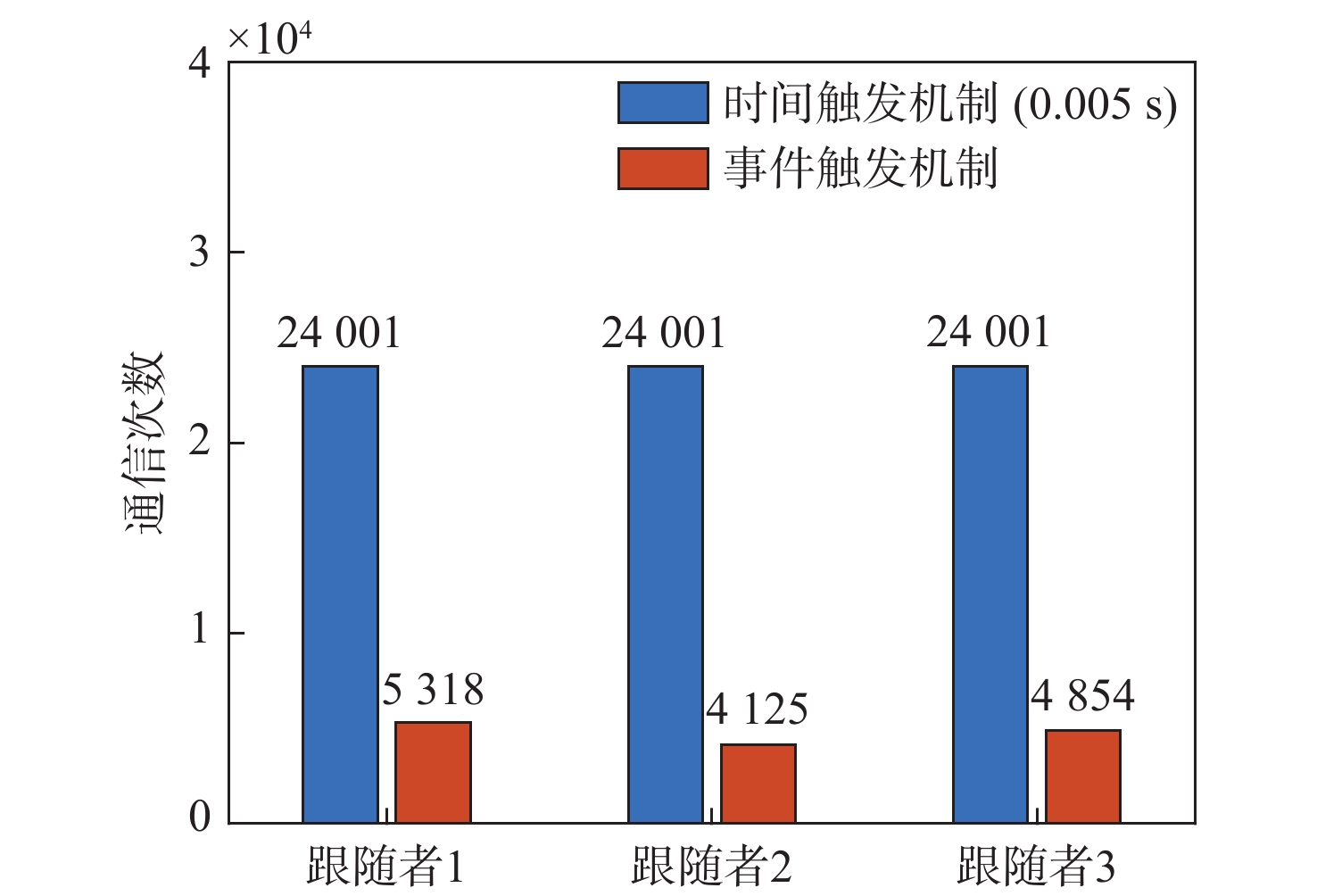
图5所示为ASV的控制输入信号,可见离散化是该触发控制命令的一个特征,系统在预定义事件为真时才会进行控制与采样。图6展示了3艘ASV的触发时间间隔图,强调了触发机制在控制过程中的作用。图7为基于时间触发方案和事件触发方案的通信次数对比图,可见编队中每艘ASV可以节省78%甚至更多的通信资源。
综上所述,通过有效降低通信频率,不仅明显减少了整个编队在控制过程中的通信总量,同时实现了良好的闭环控制性能。
4. 结 语
针对不确定外界干扰影响下的多水面无人自主航行器编队,本文提出了一种基于事件触发和仿射变换的分布式编队操纵控制方法,实现了通信网络下的编队整体机动控制,包括平移、缩放、旋、剪切及其相互组合的放射变化运动。通过理论分析,证明了该控制算法的有效性和稳定性,并通过相关仿真实验进一步验证了该算法的优势,及其在模拟海洋环境方面的适用性和优越性。基于本文提出的事件触发控制算法框架,不仅大幅降低了通信频率和通信能源消耗,还显著提高了ASV的编队机动性。
-
表 1 ASV集群轨迹规划
Table 1 Trajectory planning for multiple ASVs
障碍物类型 运动描述 一 
二 
三 
表 2 ASV的模型参数
Table 2 The model parameters of ASV
参数名称 数值 惯性质量/ kg {m_{11}} = 25.8 , {m_{22}} = 33.8 , {m_{33}} = 2.76 水动力阻尼系数 {d_{11}} = 2 , {d_{22}} = 7 , {d_{33}} = 0.5 表 3 ASV编队的初始状态
Table 3 The initial states of the ASV formation
ASV编号 数值 ASV1 {\left[{x}_{1},{y}_{1},{\psi }_{1}\right]}^{\text{T}}={\left[0.2,2,1.57\right]}^{\text{T}},{\left[{u}_{1},{v}_{1},{r}_{1}\right]}^{\text{T}}={\left[0,0,0\right]}^{\text{T}} ASV2 {\left[{x}_{2},{y}_{2},{\psi }_{2}\right]}^{\text{T}}={\left[-1,1,1.7\right]}^{\text{T}},{\left[{u}_{2},{v}_{2},{r}_{2}\right]}^{\text{T}}={\left[0,0,0\right]}^{\text{T}} ASV3 {\left[{x}_{3},{y}_{3},{\psi }_{3}\right]}^{\text{T}}={\left[1,1,1.48\right]}^{\text{T}},{\left[{u}_{3},{v}_{3},{r}_{3}\right]}^{\text{T}}={\left[0,0,0\right]}^{\text{T}} ASV4 {\left[{x}_{4},{y}_{4},{\psi }_{4}\right]}^{\text{T}}={\left[1.8,-1.8,1.6\right]}^{\text{T}},{\left[{u}_{4},{v}_{4},{r}_{4}\right]}^{\text{T}}={\left[0,0,0\right]}^{\text{T}} ASV5 {\left[{x}_{5},{y}_{5},{\psi }_{5}\right]}^{\text{T}}={\left[-2.5,-0.5,1.6\right]}^{\text{T}},{\left[{u}_{5},{v}_{5},{r}_{5}\right]}^{\text{T}}={\left[0,0,0\right]}^{\text{T}} ASV6 {\left[{x}_{6},{y}_{6},{\psi }_{6}\right]}^{\text{T}}={\left[1.1,1.2,1.6\right]}^{\text{T}},{\left[{u}_{6},{v}_{6},{r}_{6}\right]}^{\text{T}}={\left[0,0,0\right]}^{\text{T}} ASV7 {\left[{x}_{7},{y}_{7},{\psi }_{7}\right]}^{\text{T}}={\left[1,-1,1.5\right]}^{\text{T}},{\left[{u}_{7},{v}_{7},{r}_{7}\right]}^{\text{T}}={\left[0,0,0\right]}^{\text{T}} 表 4 控制方法的设计参数
Table 4 Designed parameters of control method
参数名称 数值 控制器参数 {k_1} = 17 , {k_2} = 0.14 , {k_3} = 17 , {k_4} = 0.14 , {c_1} = {c_2} = {c_3} = {c_4} = 0.1 一阶滤波器参数 {\gamma _1} = 100 , {\gamma _2} = 100 事件触发机制参数 {\beta _\rho } = 2 , {\beta _{\rho 0}} = 0.0001 , {\eta _\rho } = 0.2 -
[1] 陈浩宇, 徐海祥, 魏骁, 等. 基于KFESO的多无人艇分布式协同路径跟踪复合抗扰控制[J]. 中国舰船研究, 2025, 20(1): 191–202. doi: 10.19693/j.issn.1673-3185.03983 CHEN H Y, XU H X, WEI X, et al. KFESO-based composite anti-disturbance control for distributed cooperative path following of unmanned surface vehicles[J]. Chinese Journal of Ship Research, 2025, 20(1): 191–202 (in both Chinese and English). doi: 10.19693/j.issn.1673-3185.03983
[2] 彭周华, 吴文涛, 王丹, 等. 多无人艇集群协同控制研究进展与未来趋势[J]. 中国舰船研究, 2021, 16(1): 51–64,82. doi: 10.19693/j.issn.1673-3185.01923 PENG Z H, WU W T, WANG D, et al. Coordinated control of multiple unmanned surface vehicles: recent advances and future trends[J]. Chinese Journal of Ship Research, 2021, 16(1): 51–64,82 (in Chinese). doi: 10.19693/j.issn.1673-3185.01923
[3] 宋利飞, 徐凯凯, 史晓骞, 等. 多无人艇协同围捕智能逃跑目标方法研究[J]. 中国舰船研究, 2023, 18(1): 52–59. doi: 10.19693/j.issn.1673-3185.02974 SONG L F, XU K K, SHI X Q, et al. Multiple USV cooperative algorithm method for hunting intelligent escaped targets[J]. Chinese Journal of Ship Research, 2023, 18(1): 52–59 (in both Chinese and English). doi: 10.19693/j.issn.1673-3185.02974
[4] 沈佳颖. 多无人艇一致性自主编队控制研究[D]. 哈尔滨: 哈尔滨工程大学, 2019. SHEN J Y. Research on autonomous formation control of unmanned surface vehicles[D]. Harbin: Harbin Engineering University, 2019 (in Chinese).
[5] 王宁, 刘永金, 高颖. 未知扰动下的无人艇编队优化轨迹跟踪控制[J]. 中国舰船研究, 2024, 19(1): 178–190. doi: 10.19693/j.issn.1673-3185.03348 WANG N, LIU Y J, GAO Y. Optimal trajectory tracking control of unmanned surface vehicle formation under unknown disturbances[J]. Chinese Journal of Ship Research, 2024, 19(1): 178–190 (in both Chinese and English). doi: 10.19693/j.issn.1673-3185.03348
[6] SHAH B C, ŠVEC P, BERTASKA I R, et al. Resolution-adaptive risk-aware trajectory planning for surface vehicles operating in congested civilian traffic[J]. Autonomous Robots, 2016, 40(7): 1139–1163. doi: 10.1007/s10514-015-9529-x
[7] PENG Z H, WANG D, LI T S, et al. Leaderless and leader-follower cooperative control of multiple marine surface vehicles with unknown dynamics[J]. Nonlinear Dynamics, 2013, 74(1-2): 95–106. doi: 10.1007/s11071-013-0951-3
[8] ZHANG G Q, YU W, LI J Q, et al. A novel event-triggered robust neural formation control for USVs with the optimized leader-follower structure[J]. Ocean Engineering, 2021, 235: 109390. doi: 10.1016/j.oceaneng.2021.109390
[9] ZHANG X M, HAN Q L, ZHANG B L. An overview and deep investigation on sampled-data-based event-triggered control and filtering for networked systems[J]. IEEE Transactions on Industrial Informatics, 2017, 13(1): 4–16. doi: 10.1109/TII.2016.2607150
[10] ARRICHIELLO F, CHIAVERINI S, FOSSEN T I. Formation control of marine surface vessels using the null-space-based behavioral control[M]//PETTERSEN K Y, GRAVDAHL J T, NIJMEIJER H. Group Coordination and Cooperative Control. Berlin, Heidelberg: Springer, 2006: 1−19. doi: 10.1007/11505532_1.
[11] FU M Y, YU L L. Finite-time extended state observer-based distributed formation control for marine surface vehicles with input saturation and disturbances[J]. Ocean Engineering, 2018, 159: 219–227. doi: 10.1016/j.oceaneng.2018.04.016
[12] PENG Z H, WANG J, WANG D. Containment maneuvering of marine surface vehicles with multiple parameterized paths via spatial-temporal decoupling[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(2): 1026–1036. doi: 10.1109/TMECH.2016.2632304
[13] PENG Z H, WANG J, WANG D. Distributed containment maneuvering of multiple marine vessels via neurodynamics-based output feedback[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5): 3831–3839. doi: 10.1109/TIE.2017.2652346
[14] PENG Z H, WANG J, WANG D. Distributed maneuvering of autonomous surface vehicles based on neurodynamic optimization and fuzzy approximation[J]. IEEE Transactions on Control Systems Technology, 2018, 26(3): 1083–1090. doi: 10.1109/TCST.2017.2699167
[15] HUANG B, SONG S, ZHU C, et al. Finite-time distributed formation control for multiple unmanned surface vehicles with input saturation[J]. Ocean Engineering, 2021, 233: 109158. doi: 10.1016/J.OCEANENG.2021.109158
[16] LIU K E, JI Z J. Dynamic event-triggered consensus of general linear multi-agent systems with adaptive strategy[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2022, 69(8): 3440–3444. doi: 10.1109/TCSII.2022.3144280
[17] CHEN L M, SUN Z Q, LI C J, et al. Satellite affine formation flying with obstacle avoidance[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2019, 233(16): 5992–6004. doi: 10.1177/0954410019861474
[18] LIN Z Y, WANG L L, CHEN Z Y, et al. Necessary and sufficient graphical conditions for affine formation control[J]. IEEE Transactions on Automatic Control, 2016, 61(10): 2877–2891. doi: 10.1109/TAC.2015.2504265
[19] ZHAO S Y. Affine formation maneuver control of multiagent systems[J]. IEEE Transactions on Automatic Control, 2018, 63(12): 4140–4155. doi: 10.1109/TAC.2018.2798805
[20] LI D Y, MA G F, XU Y, et al. Layered affine formation control of networked uncertain systems: a fully distributed approach over directed graphs[J]. IEEE Transactions on Cybernetics, 2021, 51(12): 6119–6130. doi: 10.1109/TCYB.2020.2965657
[21] CONNELLY R. Generic global rigidity[J]. Discrete & Computational Geometry, 2005, 33(4): 549–563. doi: 10.1007/s00454-004-1124-4
[22] JIN X, TANG Y, SHI Y, et al. Event-triggered formation control for a class of uncertain Euler-Lagrange systems: theory and experiment[J]. IEEE Transactions on Control Systems Technology, 2022, 30(1): 336–343. doi: 10.1109/TCST.2021.3055370
[23] ZHU C, HUANG B, LU Y, et al. Distributed affine formation maneuver control of autonomous surface vehicles with event-triggered data transmission mechanism[J]. IEEE Transactions on Control Systems Technology, 2023, 31(3): 1006–1017. doi: 10.1109/TCST.2022.3208466
[24] 朱骋. 面向多约束条件的无人艇目标跟踪与集群协同控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2024. doi: 10.27060/d.cnki.ghbcu.2024.000095. ZHU C. Research on target tracking and formation maneuver control of unmanned surface vehicles[D]. Harbin: Harbin Engineering University, 2024. doi: 10.27060/d.cnki.ghbcu.2024.000095 (in Chinese).
[25] LOMBANA D A B, DI BERNARDO M. Multiplex PI control for consensus in networks of heterogeneous linear agents[J]. Automatica, 2016, 67: 310–320. doi: 10.1016/j.automatica.2016.01.039
[26] SKJETNE R, FOSSEN T I, KOKOTOVIĆ P V. Adaptive maneuvering, with experiments, for a model ship in a marine control laboratory[J]. Automatica, 2005, 41(2): 289–298. doi: 10.1016/j.automatica.2004.10.006



 下载:
下载: