0.   引　言

仿生航行体（又称“仿生鱼”）相对于传统螺旋桨推进装置具有诸多优势，被广泛应用于海洋勘测、运输管道检测和水下目标识别等领域^[1-4]，同时在鱼雷、潜艇和水下侦察无人机等军事领域也有重要应用^[5-8]。单一仿生航行体在执行长期、大范围的水下作业任务时可能存在局限性，而集群仿生鱼则能从相邻同伴产生的特殊流场中获得水动力优势，有效提高作业效率并节省能量，水下航行器的集群化是未来发展的重要方向^[8]。国内在水下航行器集群方面的研究主要以天津大学、中科院沈阳自动化研究所和西北工业大学等单位为代表^[9]。2021年7月，西北工业大学针对浅水濒海区域水下目标探测的需求，开展了水下航行器自主跟踪目标、多航行器协同探测等技术研究，其利用3台“勇毅”号水下航行器实现了集群三角队形和一字队形的快速变换及高精度保持，为形成颠覆性的探测能力奠定了基础。

现有群鱼推进性能数值模拟研究主要可以分为以下两方面：1）双鱼模型研究、2）集群运动模型研究。双鱼模型作为研究群鱼游动的简化模型，国内外学者对其进行了大量研究^[10-12]。针对双鱼模型研究，主要有并列形式的双鱼游动研究、串联形式的双鱼游动研究、双鱼间距影响研究以及波数和相位差影响研究。针对并列形式的双鱼游动研究，Dong等^[13]使用时空有限元法对并列两仿生鱼游动进行了研究，并深入分析了同相和反相波动仿生鱼的力学机制与流场结构。针对串联形式的双鱼游动研究，Jiang^[14]采用浸入边界法求解Navier-Stokes方程，数值研究了两串联仿生鱼之间的水动力相互作用，研究发现，采用串联配置似乎更有利于上游鱼，而对于后方的鱼来说，在一定条件下可以获得上游鱼尾流的优势，但在斯特罗哈数St>0.4时其性能会下降。针对双鱼间距影响研究，Wei^[15]使用三自由度鱼体自推进模型进行了研究，其通过改变初始纵向间距和初始横向间距，研究了两鱼间距对游动性能的影响，分析了鱼类的瞬态性能，如游动速度和效率，研究表明，仅靠被动水动力作用，鱼群并不能保持稳定的队形。针对波数和相位差影响研究，Pang^[16]从推进性能及效率的角度出发，研究了串联仿生鱼推进性能，分析了波数和相位差对推进性能的影响。上述研究针对的均是特定形态的双鱼运动，是理想化的模型，不能全面反映实际鱼群中个体所经历的复杂流场效应，这种简化可能会导致对实际应用效果的低估。

集群运动模型研究主要包括不同间距和激励频率对集群运动的影响研究、相位差对三角形编队运动研究、菱形编队研究以及不同间距的研究。针对不同间距和激励频率对集群运动的影响研究，辛建建^[17]基于自主研发的径向基虚拟网格法求解器，对不同间距和激励频率下阵列布置仿生鱼的水动力系数进行了深入分析，结果显示紧密布置的仿生鱼在相同运动形式下能获得更高的游动效率。针对相位差对于三角形编队运动的研究，Qi^[18]探讨了相位差变化对1个上游2个下游的三角形编队中鱼群效率的影响，结果表明，三角形阵列的最佳排列是上游鱼具有与下游鱼相反的相位，而下游两鱼具有相同的相位，此时，阵列中所有鱼的效率均高于单鱼的效率。针对菱形编队研究，Li等^[19] 针对3种不同的间距进行了深入研究，结果表明推力和侧向功率损失是影响弗劳德效率的关键因素，较小的间距会导致更高的推力，而较大的间距则会导致更低的侧向功率损失；Pan^[20]则使用尖锐界面浸入边界法针对尾鳍拍动相位差对菱形鱼群水动力性能和尾流动力学的影响进行了数值研究，通过对鱼群的水动力性能和尾流的定量分析，表明尾流模式对于预测鱼群的水动力性能至关重要，并且高度依赖相位差。针对不同间距的研究，Li^[21]通过改变仿生鱼间距，对4种不同的编队进行了研究，包括三鱼串列、三鱼并列、菱形和矩形，经比较不同群体之间的弗劳德效率发现，在小间距下，串联群体的效率最高，而在大间距下，矩形群体的效率最高。上述研究表明，排列形式和空间排列间距对群鱼游动推进性能起着至关重要的作用，然而对于游动性能与排列间距之间的影响规律，以及其作用机制与流场结构的内在关联，目前还没有统一性的研究。

本文拟聚焦于多种排列形式，重点研究空间布局对仿生鱼航行体推进性能的影响，数值研究仿生航行体推进水动力特性，探究仿生推进性能演化规律，分析仿生流场结构特征，探究多个仿生航行体在水下游动作业时水动力优势最佳、推进减阻效率最优的空间排列布局，为水下高性能航行体的研究与开发提供一定的理论参考。

1.   数值模型

1.1   数值方法

本文基于CFD软件Fluent对非定常流场进行模拟。对于牛顿流体，描述二维非定常不可压缩流动的控制方程为：

式中：u为流体的速度矢量；ρ为流体密度；f为流体体积力；p为流体压力；μ为流体动力黏度。

在Fluent求解器的选择上，基于有限体积法实现控制方程的空间离散化，使用SIMPLE算法实现连续方程的压力−速度耦合，采用高斯−赛德尔（Gauss-Seidel）线性方程求解器求解离散化后的方程。离散方式中的梯度项选择基于单元体的最小二乘法（least squares cell based）对重叠区域的单元数据进行插值，压力项选择二阶格式（second order），动量项选择二阶迎风格式（second order upwind），时间项选择二阶隐式格式（second order implict），选取层流模型对仿生鱼流场进行数值模拟，上述数值方法被广泛应用于涉及柔性变形流场的模拟中^[11,15,22]。

1.2   计算策略

基于Fluent强大的二次开发功能，采用C语言自编运动函数UDF（user-defined function，UDF）实现仿生鱼的边界柔性变形，并嵌入Fluent的主程序，以对特定问题进行数值模拟。

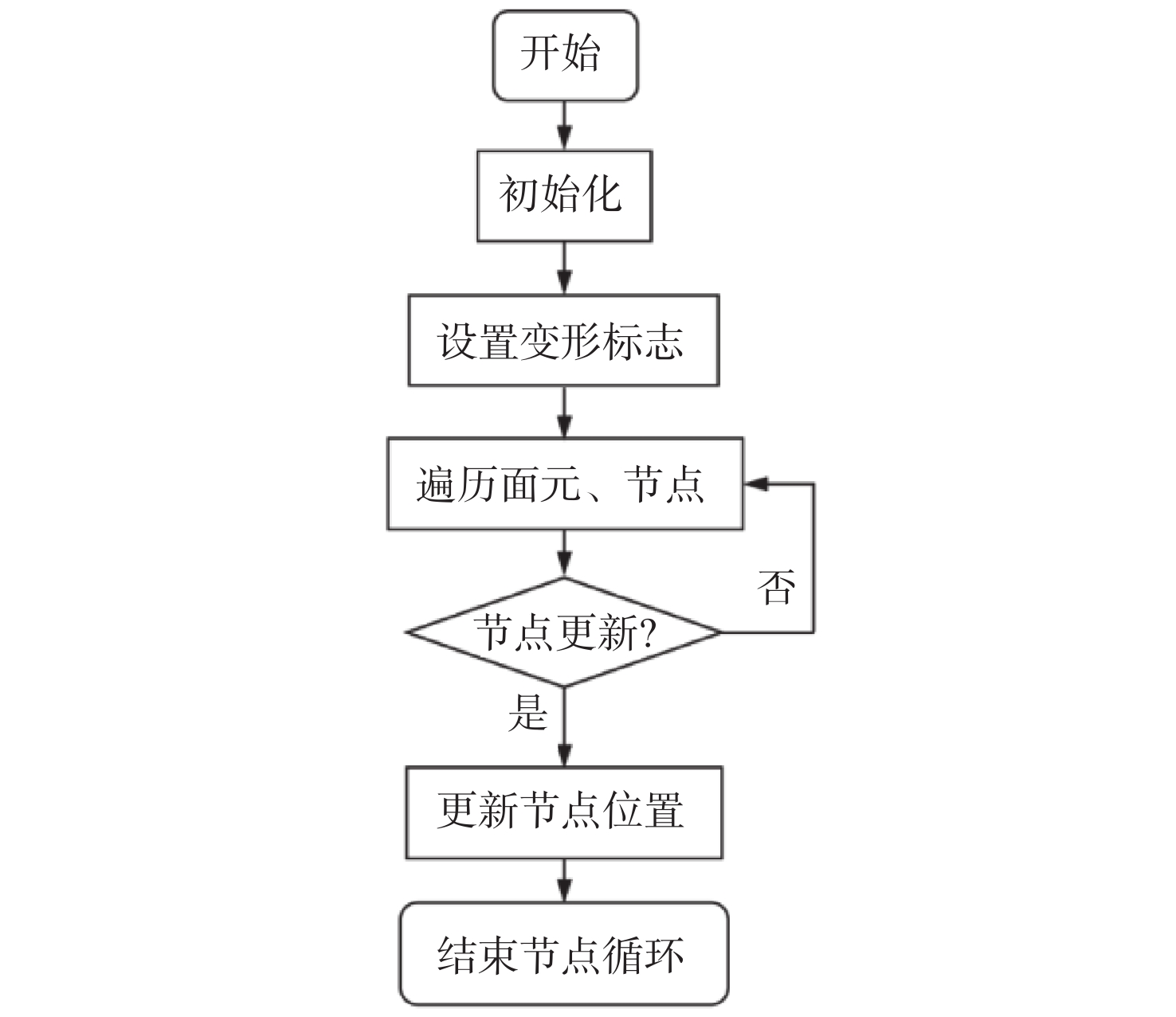
对于约束运动模型，在DEFINE_GRID_ MOTION宏命令中施加仿生鱼边界柔性变形运动方程，通过begin_f_loop(f，tf)和f_node_loop(f，tf，n)循环指令遍历网格变形区域的所有面元和节点，并读取当前时刻动网格的物理信息。通过NODE_POS_NEED_UPDATE命令检查网格节点更新状态，并通过计算当前时刻节点位置和上一时刻节点位置来更新节点位移坐标，最后结束节点循环，实现仿生鱼边界柔性运动。其计算流程图如图1所示。

图  1  仿生鱼边界节点更新流程图

Figure  1.  Flowchart for the boundary node update process of bionic fish

下载: 全尺寸图片 幻灯片

此外，仿生鱼表面网格的柔性变形会导致计算域内网格拓扑结构变化，因此，加入动网格方法对网格进行实时更新。本文中动网格更新方法采取将扩散光顺法与局部网格重构法相结合的方法。通过扩散光顺法，对计算域中涉及变形的网格进行总体的变形控制，局部网格重构法则用于对局部变形过大的网格进行重构更新，以确保得到满足计算需求的新网格。动网格设置包括光顺、分层和网格重构，具体设置如下：光顺采用扩散光顺法（diffusion）；分层划分采用基于高度的划分方法，其中拆分因子（split factor）取为0.4，合并因子（collapse factor）取为0.2；网格重构法采用局部单元（local cell）和局部面（region face）选项，在网格重新生成的过程中，动网格最小尺寸要大于网格属性中的最小长度尺寸（minimum length scale），动网格最大尺寸则小于网格属性中的最大长度尺寸（maximum length scale），最大网格单元非均匀度（maximum cell skewness）取为0.7，网格重构尺寸间隔（size remeshing interval）取为5。

2.   数值模型及验证

2.1   模型设置

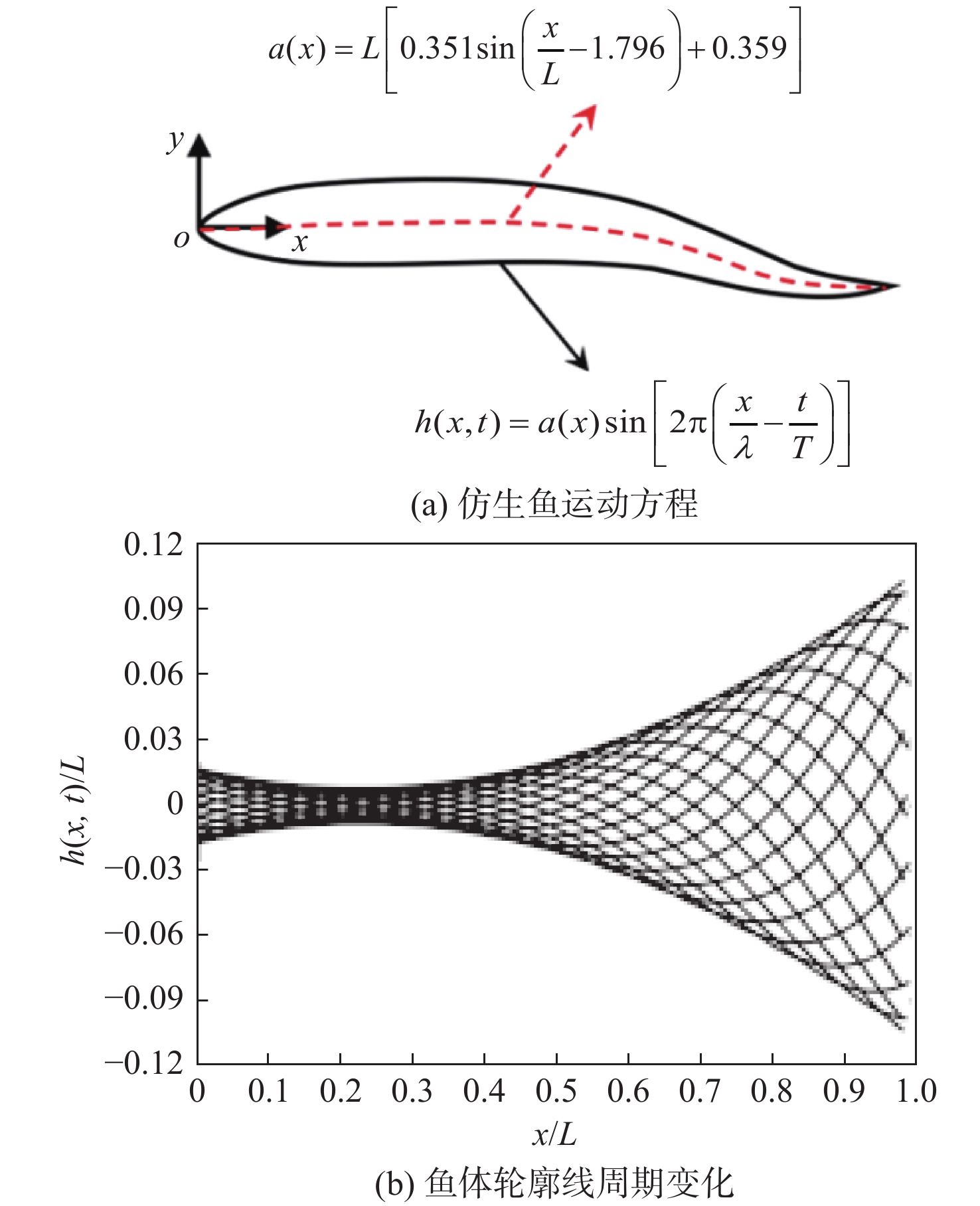
首先建立计算模型，本文以NACA 0012翼型代替仿生鱼，推进模式设置为亚鲹科游动模式，该运动模式常被用来模拟小型鱼类（鳟鱼）的游动。仿生鱼体表面横向波动方程可描述为^[23]：

式中：h(x，t)为仿生鱼轮廓线横向位移距离，如图2所示；a(x)为鱼体中心线横向波动的振幅包络线；x为仿生鱼体表面某一点距头部的流向距离；λ为鱼体波长；T = 1/f，为摆动周期，鳟鱼在自由来流时波长λ和频率f通常为定值^[24]，即λ = 1.15，f = 6.67。

图  2  仿生鱼运动模型示意图

Figure  2.  Schematic diagram of the bionic fish motion model

下载: 全尺寸图片 幻灯片

a(x)的表达式如下：

式中， L = 0.1 m，为鱼体长度。

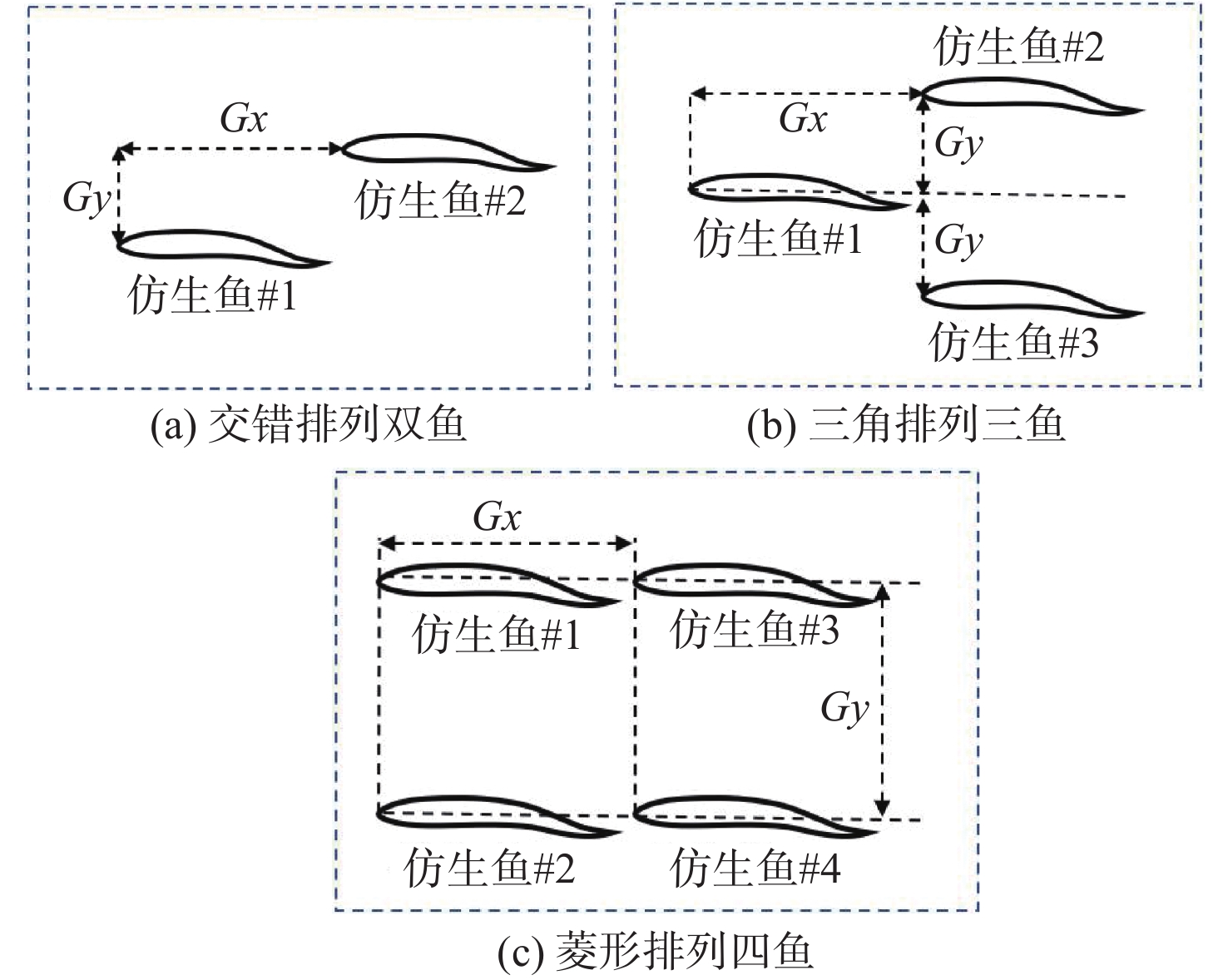
本文对交错排列、三角形排列、矩形排列队形下的仿生鱼运动进行了数值模拟研究，队形示意图如图3所示。图中，Gx，Gy为无量纲间距，即实际布置间距与鱼体长度的比值。当仿生鱼的排列间距过大时，将不会发生显著的干扰作用，而在间距较小时，由于身体的摆动会发生碰撞，故本文针对不同队形布置选取了合适的间距进行研究。交错排列如下：0≤Gx≤4.0，0≤Gy≤2.0，三角形排列如下：0≤Gx≤4.0，0.3≤Gy≤1.0，矩形排列如下：1.5≤Gx≤4.0，0.3≤Gy≤2.0。

图  3  仿生鱼队形示意图

Figure  3.  Schematic diagram of bionic fish formation

下载: 全尺寸图片 幻灯片

开始计算之前，有必要对仿生鱼游动涉及到的水动力参数进行说明，雷诺数是表征流体运动状态的重要参数，代表单位质量流体的惯性力与粘性力之比：

式中：u = 0.45 m/s，为来流速度；μ为流体动力黏度，本文中流体介质为水。

表征非定常流体动力学的另一个重要参数是斯特劳哈尔数St，其定义如下：

式中，A = 2L，为鱼尾所穿越最大横向振幅的2倍。阻力F_d为仿生鱼流向受力，升力F_l为流向法向受力，二者均由鱼体表面的压力和剪切应力积分计算得到。本文对仿生鱼施加固定约束，采用无量纲阻力系数C_d和升力系数C_l来表征阻力与升力，定义如下：

当阻力的方向与流动方向相反时，认为仿生鱼受到了推力，因此，推力系数可以表示为

为直观探究多个仿生鱼推力系数的变化趋势，采用无量纲平均推力系数进行描述，表达式如下：

式中：$\overline {C_{\mathrm{t}}^i}$(i = 1，2，3…)为第i条仿生鱼的无量纲推力系数；$\overline {{C_{\mathrm{t}}}}$为仿生鱼平均推力系数；$\overline {{C_{{\mathrm{ts}}}}}$为单条仿生鱼平均推力系数。显然，当$\overline {C_{\mathrm{t}}^i}$>1时，表明其推力大于单鱼的，当无约束力存在时仿生鱼将加速向前游动；$\overline {C_{\mathrm{t}}^i}$ < 1则说明其推力小于单鱼的，当无约束力存在时仍能向前游动；而当$\overline {C_{\mathrm{t}}^i}$< 0时，则表示此时仿生鱼受到的力为阻力，当无约束力存在时将不能向前游动。

2.2   数值验证

针对单条仿生鱼游动展开数值验证，计算域如图4（a）所示。仿生鱼体长L，计算域长20L、宽10L，鱼体前端距入口边界4.5L；入口为速度入口边界（velocity inlet）；出口为压力出口边界（pressure outlet），相对压力为0；上、下边界为对称边界（symmetry）；鱼体表面为壁面边界（wall），施加不可滑移边界条件。网格划分情况如图4（b）所示。网格划分为2部分：内部区域涉及仿生鱼表面运动，采用三角形非结构网格进行局部加密，以便于更好地捕捉仿生鱼的表面力；外部区域采用规整的结构化网格，网格尺寸由内向外逐渐递增。

图  4  计算域边界条件及网格划分

Figure  4.  Boundary conditions and mesh generation of the computational domain

下载: 全尺寸图片 幻灯片

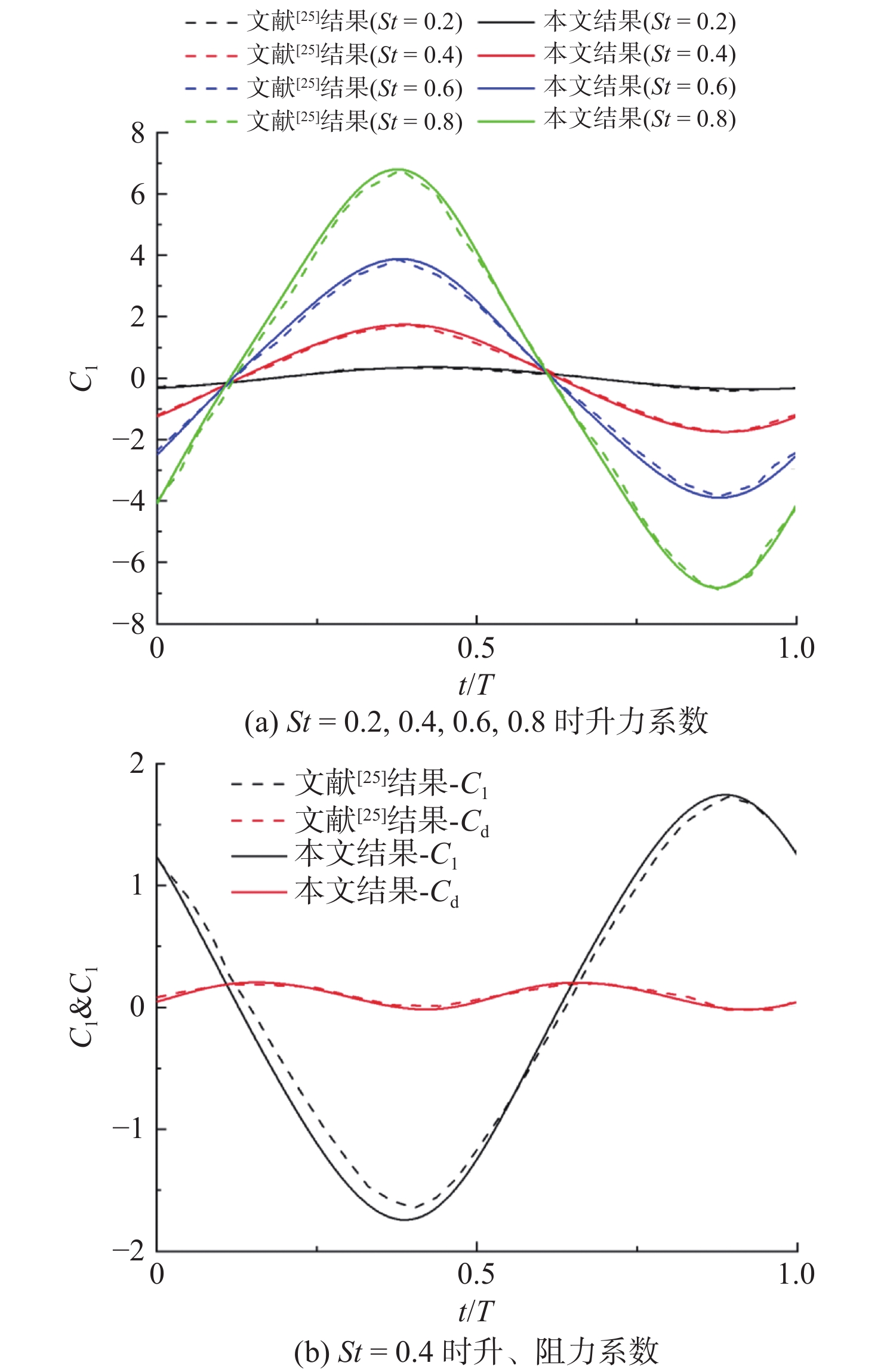
与文献[25]的计算结果进行对比，对St = 0.2，0.4，0.6，0.8的鱼体升、阻力系数在一个周期内的时历曲线进行验证，结果如图5所示。图中，虚线代表文献[25]中计算结果，实线代表本文计算结果，对比结果显现出较好的吻合性，证明了本文计算方法的有效性。

图  5  升阻力系数验证

Figure  5.  Verification of the lift-to-drag coefficient

下载: 全尺寸图片 幻灯片

3.   数值结果与讨论

3.1   交错排列仿生鱼游动分析

3.1.1   平均推力特性分析

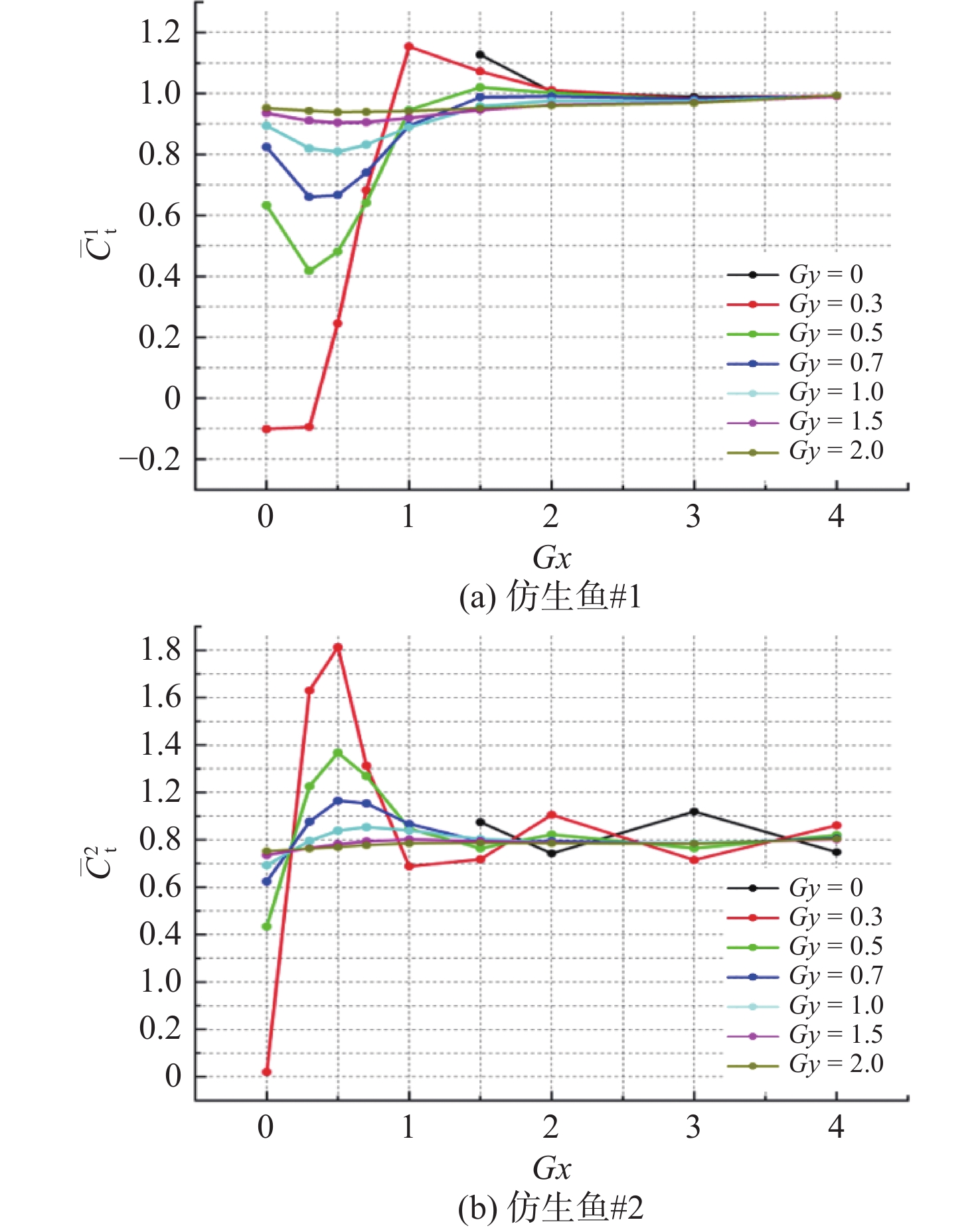
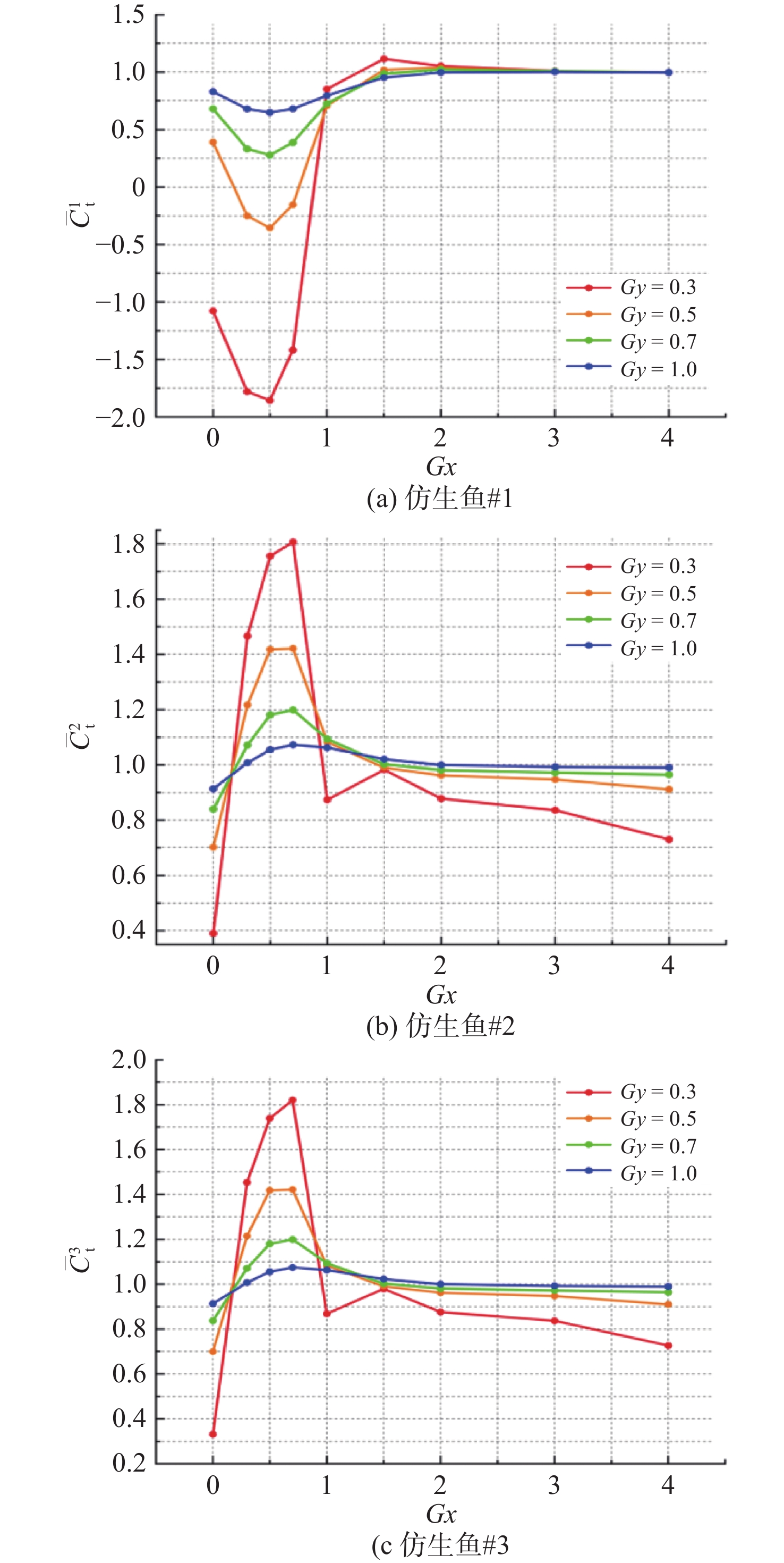
图6（a）展示了仿生鱼#1在不同纵向间距Gx和横向间距Gy下的变化曲线。从中可以发现：1）当Gy = 0时，2条仿生鱼串列布置，仿生鱼#1的推力系数随Gx的增大呈逐渐减小趋势，在Gx = 1.5时平均推力系数较单鱼的游动提升了12.3%；2）当Gy = 0.3，Gx < 0.5时，平均推力系数小于0，此时由仿生鱼波动产生的推力小于受到的流体阻力，无法向前推进。随着Gx的增大，推力系数大于0并逐渐增加，在Gx = 1.0时推力达到峰值，相比单鱼提升了15.3%。随着Gx的继续增大，平均推力系数逐渐稳定趋于1；3）当Gy > 0.3，在Gx较小时推力系数均小于1，表明此时流场的干扰对推力的影响是负面的。随着Gx的增大，平均推力系数经历先降低再增加的转折，在转折点之后，流场对仿生鱼的干扰开始向有利的方向转变。随着Gx的继续增大，推力系数接近于1，此时仿生鱼的游动特性与单条仿生鱼的游动并无差异。从整体上看，除串列布置外，仿生鱼#1的推力系数随Gx的增大呈先减小后增大并最终趋近于1的趋势，各横向间距Gy均在Gx = 0.5附近达到最小值，表明此间距下两鱼产生的水动力干扰对仿生鱼#1是最不利的。

图  6  平均推力系数

Figure  6.  Average thrust coefficients

下载: 全尺寸图片 幻灯片

图6（b）所示为仿生鱼#2的平均推力系数随Gx和Gy的变化曲线。整体而言，在Gx很小时，仿生鱼受到流场的负面干扰，随着Gx的增大，平均推力系数也开始增加。仿生鱼平均推力系数最大值在[(Gx, Gy) = (0.5, 0.3)]处，相比单鱼的游动提升了81.3%。在Gx>0.5之后，不同Gy下的仿生鱼表现出不同的推力特性：1）当Gy ≤ 0.3时，平均推力系数呈现波动变化；2）当Gy = 0.5，0.7，1.0时，平均推力系数单调减小并最终趋于1；3）当Gy >1.0时，平均推力系数随着Gx的增加无明显变化，始终保持在1附近。

结合两鱼的推力系数曲线可以发现，随着Gy的增大，平均推力系数曲线的变化幅度逐渐减小，说明横向间距增大，2条仿生鱼之间的干扰减弱。随着Gx的增大，仿生鱼#1的推力系数呈先减小后增大最终趋于1的趋势，仿生鱼#2的推力系数则呈现出先增大后减小并最终围绕1上下波动的趋势。值得注意的是，当纵向间距Gx = 0时，2条仿生鱼的推力均小于1，说明两鱼相距过近时所受到的干扰是无益的。

3.1.2   尾涡特性分析

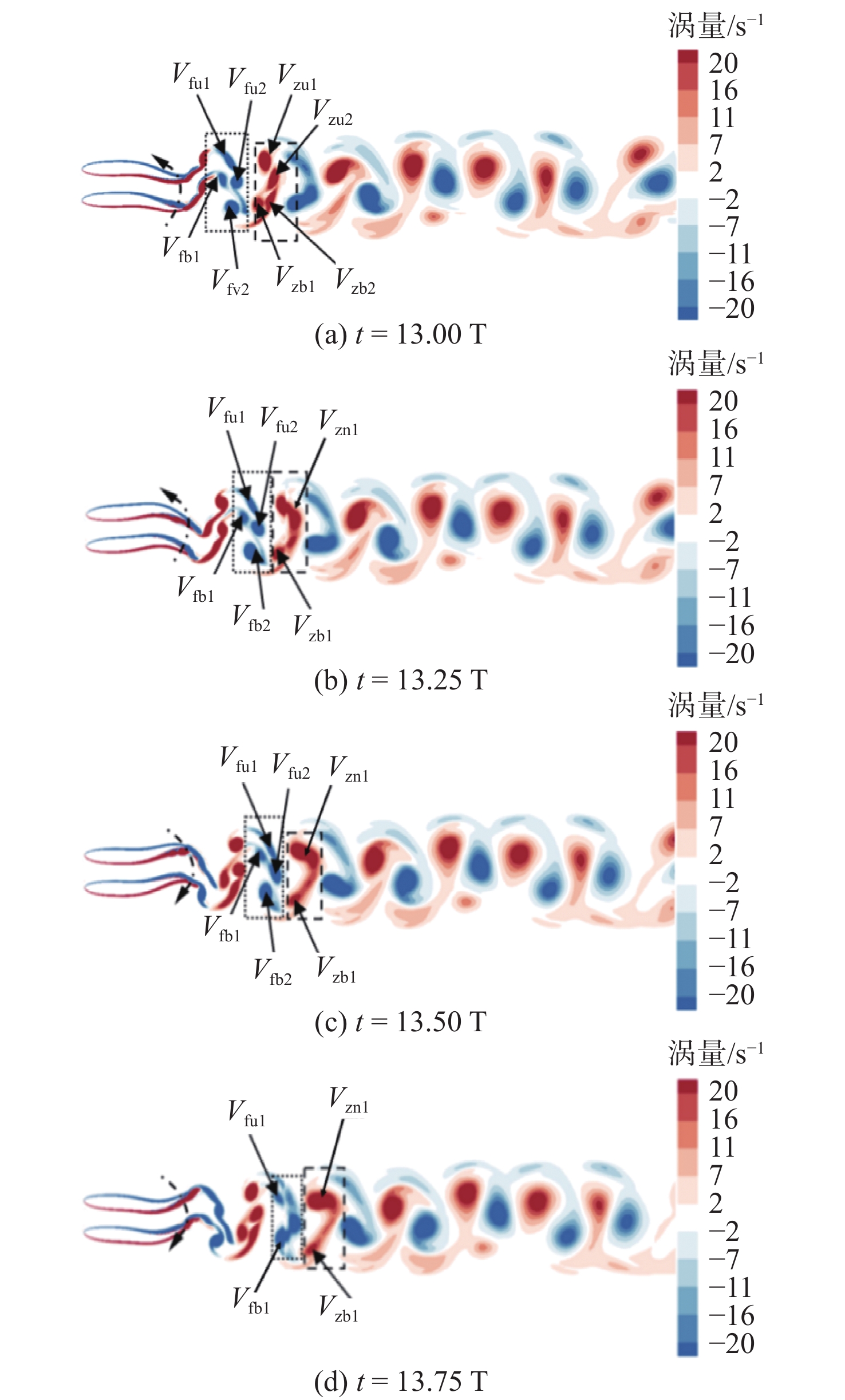
当Gx = 0时，两仿生鱼的推力系数较其他间距下仿生鱼的推力系数均存在显著降低，故针对该间距下仿生鱼一个周期内的漩涡脱落给出具体分析。图7所示为[(Gx, Gy) = (0, 0.3)]时一个周期内的尾涡演化结果,其中t代表时间，T代表周期。此时，2条仿生鱼并排游动，图中虚线箭头为鱼尾摆动方向。在一个周期开始时，如图7（a）所示，上侧仿生鱼尾部脱落的负涡（图中蓝色的涡）分裂成V_fu1和V_fu2两个小涡，正涡（图中红色的涡）分裂成V_zu1和V_zu2两个小涡；下侧仿生鱼尾部脱落的负涡分裂成V_fb1和V_fb2两个小涡，正涡分裂成V_zb1和V_zb2两个小涡。在1/4个周期后，如图7（b）所示，V_zu1，V_zu2与V_zb2逐渐合并重组成一个新的涡V_zn1，V_zb1逐渐远离。当t = 13.5T时，如图7（c）所示，V_fu1，V_fu2与V_fb2逐渐合并重组成一个新的涡，V_fb1开始远离。当t = 13.75T时，V_zb1和V_fb1进一步远离之前新重组的涡，如图7（d）所示。一个周期结束之后，新组成的正涡V_zn1逆时针向后传递，新组成的负涡V_fn1顺时针向后传递，反卡门涡街形成。而之前远离的V_zb1和V_fb1则在远场逐渐发散，V_zb1和V_fb1分别与下一周期新组成的负涡和正涡相互抵消，使得整个涡场强度被削弱。这也就很好地解释了在[(Gx, Gy) = (0, 0.3)]时，2条仿生鱼的平均推力系数相较于其他间距呈现出显著降低的现象。随着Gy的增加，并列仿生鱼之间的尾涡削弱程度得以减轻，所以当Gx = 0时平均推力系数随Gy的增加逐渐增大。

图  7  [(Gx, Gy) = (0, 0.3)]时的流场涡量云图

Figure  7.  Vorticity contours of the flow field at [(Gx,Gy) = (0, 0.3)]

下载: 全尺寸图片 幻灯片

3.1.3   流场压力和速度特性分析

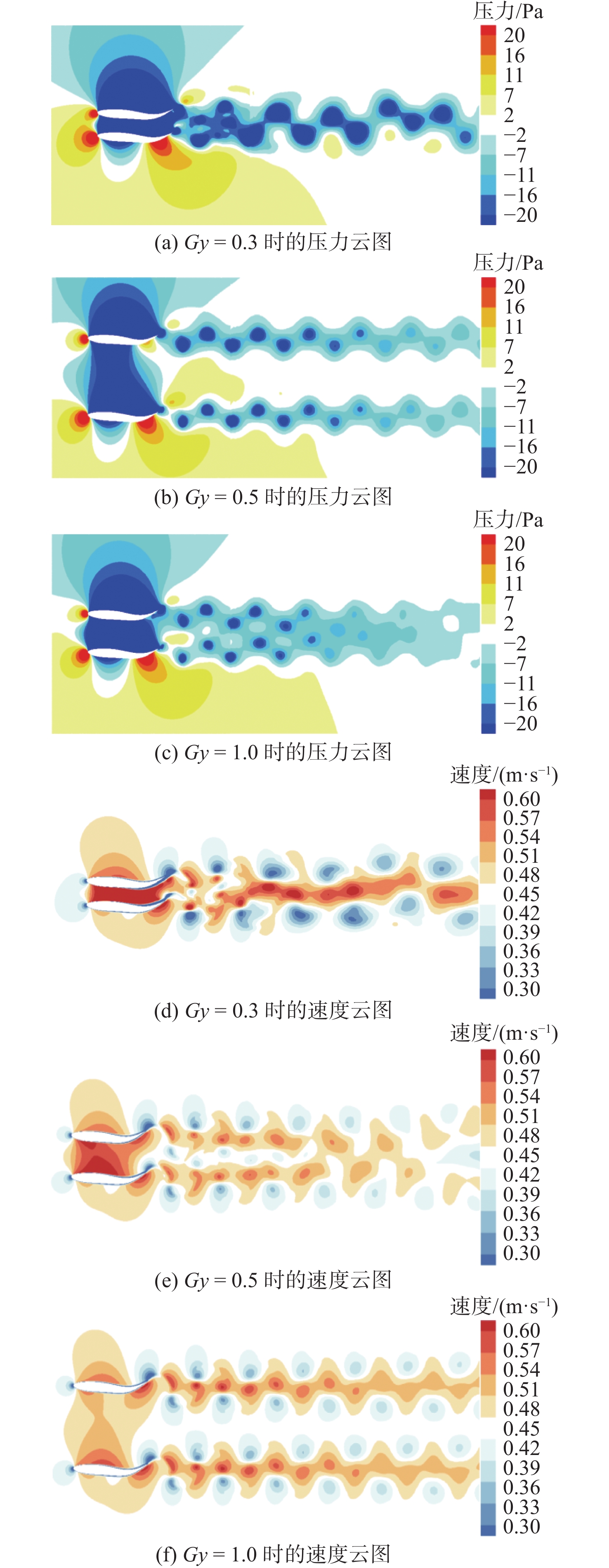
图8所示为部分横向间距下两仿生鱼并列排列的压力和速度云图。由图可见，在Gy = 0.3时，两鱼横向间隙很小，流体通过时受挤压，流向速度急剧增大，根据伯努利原理，两鱼之间的间隙为负压；同时，两鱼头部出现正压区合并，尾部出现负压区合并，导致鱼体前端近场正压区增强，尾部远场负压区增强，正负压联合作用致使两鱼的推力系数减弱，如图8（a）和图8（d）所示；随着Gy的增大，2条仿生鱼头部的正压区分离，尾流负压强度降低，耗散率增加，尾部逐渐有射流（即速度云图中仿生鱼尾部黄、橙色区域）产生，如图8（b）和图8（e）所示；当Gy增大到1.0时，仿生鱼尾部射流逐渐加强，两列涡街关于仿生鱼连线的中轴线对称分布，如图8（c）和图8（f）所示。随着Gy的增加，2条仿生鱼间的负压区分离，表面压降趋于一致，导致流体动量变化差异减小。因此，涡街流速上下对称且相等，仿生鱼的游动类似于单鱼，这也就解释了Gx = 0时平均推力系数变化的原因。

图  8  Gx = 0时的流场压力与速度云图

Figure  8.  Flow field pressure and velocity contours at Gx = 0

下载: 全尺寸图片 幻灯片

3.2   三角排列仿生鱼游动分析

3.2.1   平均推力特性分析

图9（a）所示为仿生鱼#1的平均推力系数变化曲线。由图可见，随着Gx的增大，平均推力系数首先减小，在Gx = 0.5处达到最小值，在Gx = 0.5之后推力系数开始递增，最终趋近于单鱼游动的情况；在Gx < 1.5时，平均推力系数均小于1（除了Gy = 0.3的小部分），说明在该间距排列下仿生鱼并未受到推力增益，并且在Gy = 0.3和Gy = 0.5时还出现了反方向的推力；在[(Gx, Gy) = (1.5, 0.3)]处，出现了平均推力系数最大值，但提升不高，仅为11.5%。图9（b）和图9（c）所示为仿生鱼#2和仿生鱼#3的平均推力系数曲线。仿生鱼#2和仿生鱼#3这两鱼关于流场中轴线对称排布，水动力性能呈现高度的一致性。当Gx = 0时，上游鱼#1位于下游两鱼中间，内部流体受到挤压，呈现很强的负压作用，导致推力系数呈现负值，而下游鱼则与双鱼游动类似，三鱼头部均出现正压区合并，尾部出现负压区合并，导致鱼体前端近场正压区增强，尾部远场负压区增强，正负压联合作用致使三鱼推力系数减弱；随着Gx的增大，平均推力系数递增，在Gx = 0.7处达到峰值，在[(Gx, Gy) = (0.7, 0.3)]处最大推力提升至80%以上；在Gx>0.7之后，推力系数逐渐下降。

图  9  平均推力系数

Figure  9.  Average thrust coefficients

下载: 全尺寸图片 幻灯片

通过对多仿生鱼的平均推力曲线进行分析可以发现，三角形排列对于上游仿生鱼的水动力性能几乎没有提升，但会给下游两鱼带来推力的提升。当0≤Gx≤1.0时，上游仿生鱼的推力系数会随Gx的增加先减小后增大，而下游两鱼则呈现先增大后减小的趋势。这表明间距较小会给上游鱼带来不利的干扰，但有益于下游鱼，且干扰程度会随Gy的增大逐渐减小。

3.2.2   尾涡特性分析

可以明显观察到，当Gy = 0.3时，三鱼的推力系数较其他间距下均有较大变化，故对此状态下不同Gx时的涡量场进行分析。图10所示Gy = 0.3时不同Gx下的流场涡量云图。当Gx较小时，如图10（a）和图10（b）所示，受下游鱼尾部摆动的诱导作用，上游鱼脱落的涡V_z1和V_f1分向两侧偏转，漩涡脱落不完整，涡强度降低；而下游两鱼漩涡在脱落前就在尾部附着区域得到增强，尾涡强度增大，所以上游鱼的推力系数很低，而下游鱼的推力系数则很高。当Gx继续增大，如图10（c）和图10（d）所示，此时上游鱼尾部漩涡V_z1和V_f1脱落逐渐完整，但仍然会受到下游鱼摆尾的略微影响，推力系数开始增大。当Gx增至3.0之后，如图10（e）和图10（f）所示，因下游鱼相距较远，上游鱼几乎不受影响，尾部出现明显的反卡门涡街，此时上游鱼的游动与单鱼游动无异；而在下游鱼尾部则出现了强烈的涡旋撕裂、融合与重组现象，导致下游鱼尾流水动力性能非常不稳定，随着后两鱼横向间距的增大，这种水动力不稳定的现象逐渐减弱。

图  10  Gy = 0.3时的流场涡量云图

Figure  10.  Vorticity contours of the flow field at Gy = 0.3

下载: 全尺寸图片 幻灯片

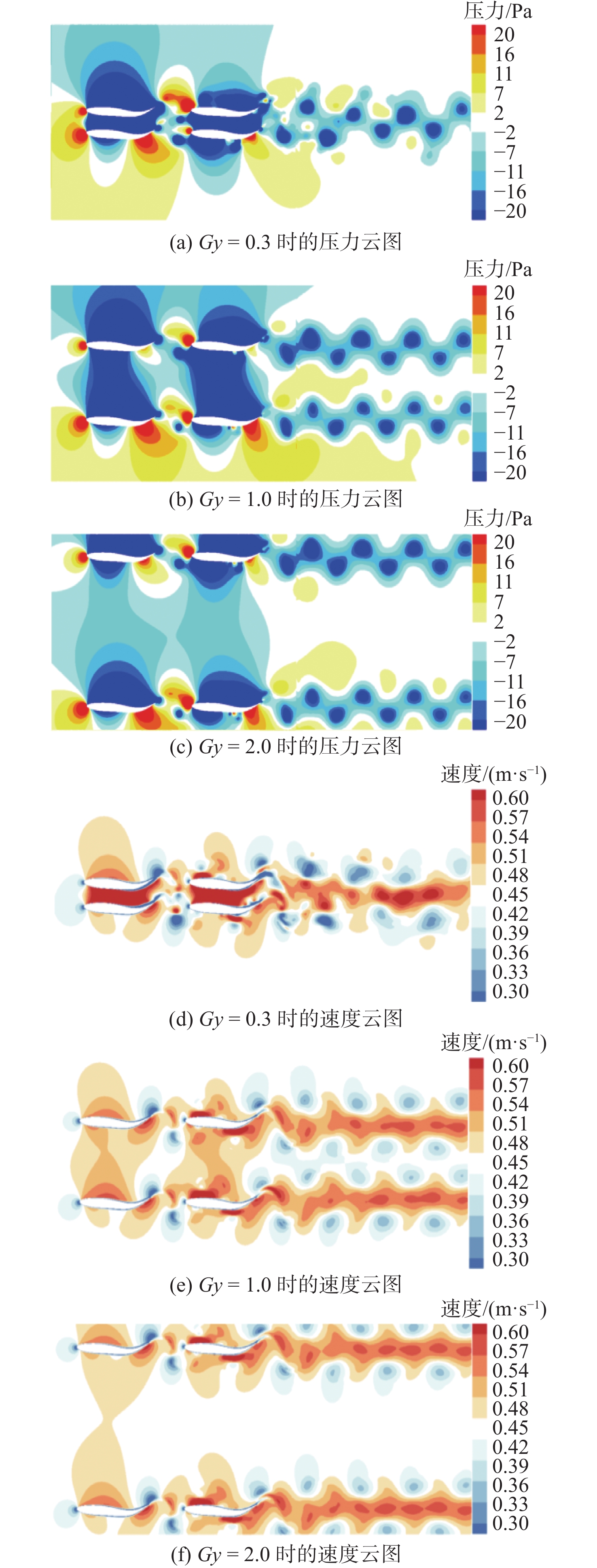
3.2.3   流场压力和速度特性分析

图11所示为Gy = 0.3时不同Gx下的流场压力与速度云图。如图11（a）和图11（d）所示，当Gx = 0.5时，3条仿生鱼相距较近，上游鱼置身于鱼群间的负压区，受到拖曳阻力，因上游鱼受到的抽吸力最大，所以平均推力系数最低；上游鱼的尾涡穿过低压区向两侧偏转，增强了后两鱼的尾流强度，故后两鱼的平均推力系数很高。如图11（b）和图11（e）所示，随着Gx的增大，上游鱼逐渐远离负压区，所受到的抽吸力减小；同时，在下游鱼头部正压区的推动下，推力系数有所提升。可注意到，当Gx = 1.5时，后两鱼尾部形成了一股非常强劲的射流，在射流的作用下推力系数略有提升。如图11（c）和图11（f）所示，上游鱼和后两鱼相距较远，上游鱼脱落的尾涡传递到下游鱼时能量已经消耗殆尽，故施加给下游鱼的影响微乎其微；而后两鱼并列游动，与图8（a）类似，尾涡的融合重组致使仿生鱼#2和仿生鱼#3的平均推力系数持续降低，而仿生鱼#1则类似于单鱼的游动。

图  11  Gy = 0.3时的流场压力与速度云图

Figure  11.  Flow field pressure and velocity contours at Gy = 0.3

下载: 全尺寸图片 幻灯片

3.3   矩形排列仿生鱼游动分析

3.3.1   平均推力特性分析

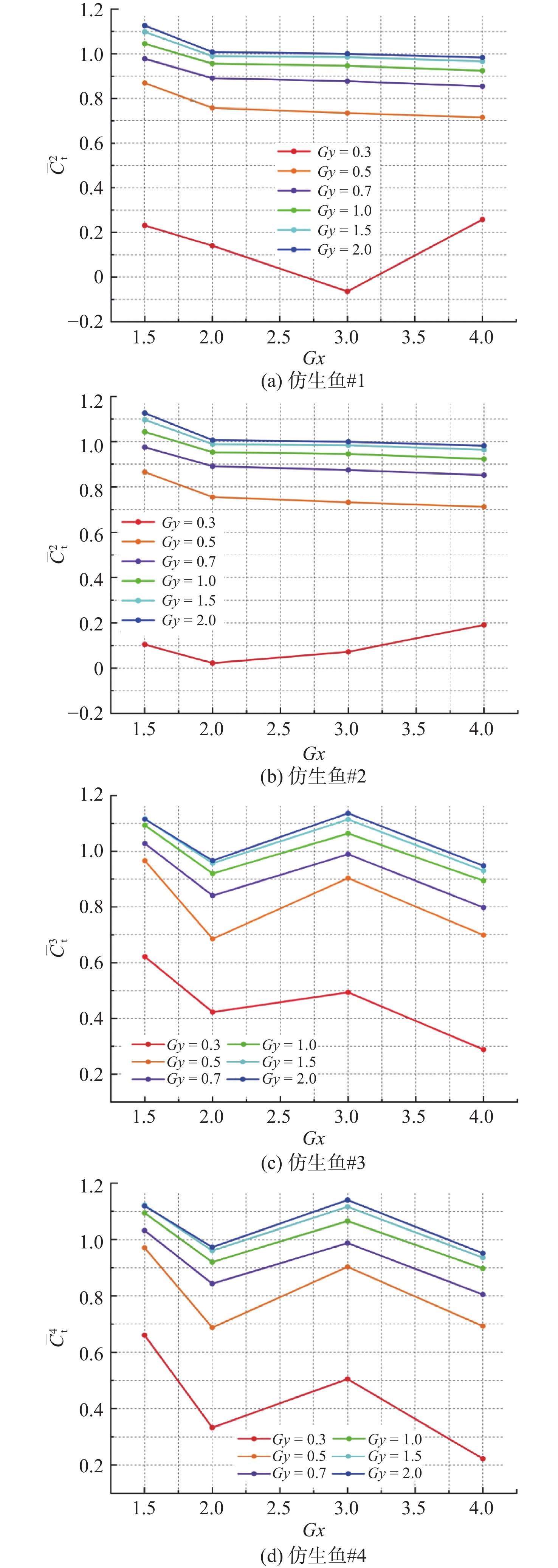
图12（a）和图12（b）示出了矩形排列中仿生鱼#1和仿生鱼#2的平均推力系数随Gx，Gy的变化曲线。从中可以发现，当Gy > 0.3时，各横向间距下平均推力系数的变化趋势一致，此时，上游两鱼之间的干扰较小，纵向间距Gx是影响推力变化的主要因素，两鱼的推力系数随Gx的增大而减小，表明间距较小会给上游鱼带来有益的干扰；而当Gy = 0.3时，平均推力系数随Gx的增加呈先减小后增大的趋势，仿生鱼#1的平均推力系数在Gx = 3.0达到最小值，下降了106.4%，仿生鱼#2的平均推力系数则是在Gx = 2.0时最小，下降了97.8%。总体而言，仅有Gy≥1.0并且Gx < 2.0的一部分区间存在推力增大现象，最大值出现在[(Gx, Gy) = (1.5, 2.0)]处，推力提升了11.3%。平均推力系数随着Gy的增大而增大并逐渐趋近于1，表明随着横向间距Gy的增加，仿生鱼趋近于单鱼的游动。

图  12  平均推力系数

Figure  12.  Average thrust coefficients

下载: 全尺寸图片 幻灯片

图12（c）和图12（d）示出了矩形排列中仿生鱼#3和仿生鱼#4的平均推力系数随Gx，Gy的变化曲线。从中可以发现，对比上游鱼的推力系数变化，下游鱼受尾流的影响推力系数变化更为剧烈。两鱼的推力系数随Gx的增大呈现上下波动趋势，在Gx = 2.0，4.0处推力系数出现显著下降，表明此时上游鱼的尾涡干扰对下游鱼的推力系数增强是无益的；在Gx = 1.5，3.0处推力系数出现显著上升，表明此时上游鱼的尾涡干扰对下游鱼的推力系数增强是有益的。在所有纵向间距Gx下，下游两鱼的推力系数随横向间距Gy的增大有略微的增大，这表明对于并列布置于尾涡流场的两鱼，过近的布置间距会给各自的推力造成不利影响。

3.3.2   尾涡特性分析

通过对图12分析，仿生鱼#3和仿生鱼#4的平均推力系数随着纵向间距Gx的增大呈现先减小后增大再减小的现象，Gx = 3.0下的平均推力系数在图中是拐点，为了探究这种现象，故展示了该间距下的仿生鱼流场涡量图。图13所示为Gx = 3.0时不同Gy下的流场涡量云图。如图13（a）所示，当Gy = 0.3时，尾涡演化过程与双鱼并列时类似，脱落的漩涡经历了分裂、融合、重组和撕裂等复杂的变化，流场形态繁杂，水动力性能紊乱，平均推力系数低下。如图13（b）所示，当Gy增加到0.5时，流场紊乱的现象得到缓解，平均推力系数有所提升。如图13（c）～图13（f）所示，当Gy > 0.5时，仿生鱼间的横向作用减小，此时下游鱼相距较远，上游鱼受干扰不明显，游动形态类似于单鱼的游动。上游鱼产生的漩涡在下游鱼尾部与下游鱼产生的旋向相同的漩涡相融合，增强了下游鱼尾部的涡场强度，所以下游鱼的平均推力系数均大于上游鱼。

图  13  Gx = 3.0时的流场涡量云图

Figure  13.  Vorticity contours of the flow field at Gx = 3.0

下载: 全尺寸图片 幻灯片

3.3.3   流场压力和速度特性分析

仿生鱼#3和仿生鱼#4在Gx = 1.5时，其平均推力系数比其他纵向间Gx下的平均推力系数有所提升。显然，此情形与Gx = 3.0 时远场尾涡致推力系数提升不同，此处的近场压强与流速干扰影响更大，具体表现为：当Gx = 1.5时，仿生鱼#4不仅受到静压，还受到仿生鱼#3的尾流作用，而随着距离的增加，当Gx = 3.0时，仿生鱼#4受到仿生鱼#3的尾流作用会降低，故展示此间距下的流场压力与速度云图。图14所示为Gx = 1.5时不同Gy下的流场压力与速度云图。如图14（a）和图14（d）所示，当Gy较小时，横向干扰较强，黏性摩擦力很大，尽管下游鱼的头部出现了正压区，但上游鱼的推力仍很低；当Gy增大至0.5时，横向干扰减弱，上游鱼推力增加，同时，下游鱼电费尾流速度增大，推力也增大。如图14（b）和图14（e）所示，当Gy进一步增大，仿生鱼#1和仿生鱼#2，仿生鱼#3和仿生鱼#4间隙处的负压区强度降低，横向作用不再占主导地位；下游鱼头部的正压给上游鱼施加了推力，下游鱼尾部开始出现独立的射流。如图14（c）和图14（f）所示，当Gy > 1.0时，下游鱼头部的正压依然存在，黏性摩擦力不足以抵消下游鱼头部正压区的推力，上游鱼获得推进优势；随着Gy的增大，横向作用减弱，下游鱼的平均推力系数增大。

图  14  Gx = 1.5时的流场压力与速度云图

Figure  14.  Flow field pressure and velocity contours at Gx = 1.5

下载: 全尺寸图片 幻灯片

4.   结　论

本文基于约束运动模型，对交错布置双鱼体、三角形布置三鱼体、矩形布置四鱼体的位置特征进行研究，并对平均推力系数、尾涡结构和流场特性进行了分析，主要得到如下结论：

1）对于交错排列双鱼，当Gx = 0时，两鱼的正负涡量相互抵消导致推力系数低下；当0<Gx<1.0时，仿生鱼#1的推力系数先减小后增大，至Gx = 1.0时推力达到最大；而仿生鱼#2的推力系数变化则与之相反，在Gx = 0.5时推力最大；随着Gx，Gy的增大，两鱼间的相互干扰减弱，推力系数趋于平稳，并最终趋近于单鱼的推力。

2）对于三角形排列仿生鱼，当0<Gx<1.0时，上游仿生鱼#1的游动受下游两鱼之间负压区的影响，推力系数显著降低，且Gy越小，负压越强，推力系数越低；下游两鱼的推力系数随着Gx的增加呈先增大后减小的趋势，这表明三鱼之间仅在Gx较小时出现强干扰。

3）对于矩形排列仿生鱼，推力系数均随Gy的增大而增加，在Gx较小时，上游两鱼可利用下游鱼的头部正压区产生推力收益，而下游的两鱼则会一直受到上游鱼尾涡的影响，推力系数随Gx的变化呈振荡趋势。

本文旨在研究不同水下多个仿生鱼布置形式对于推进性能的影响，未来的研究将着重开展多种参数下仿生鱼集群游动的数值模拟，系统考虑不同工况对推进性能的影响。后续，将开展一系列的研究，以期能够获得更为全面的认识，揭示影响仿生鱼集群游动效率的关键因素。