基于多物理模型融合仿真的波浪对船舶动力系统加速性能的影响

丁宇; 谭泉; 随从标; 向拉

doi:10.19693/j.issn.1673-3185.04437

基于多物理模型融合仿真的波浪对船舶动力系统加速性能的影响

哈尔滨工程大学动力与能源工程学院，黑龙江哈尔滨 15000

基金项目:

国家自然科学基金资助项目（52201360）

详细信息

作者简介:
丁宇，男，1980年生，博士，教授，博士生导师。研究方向：船舶动力系统性能优化与匹配设计。E-mail：dingyu@hrbeu.edu.cn

随从标，男，1989年生，博士，讲师，硕士生导师。研究方向：船舶动力系统性能仿真。E-mail：congbiao_sui@hrbeu.edu.cn

通讯作者:
随从标

中图分类号: U664.1
计量
- 文章访问数: 84
- HTML全文浏览量: 23
- PDF下载量: 2
出版历程
- 收稿日期: 2025-05-30
- 修回日期: 2025-05-22
- 网络出版日期: 2025-05-25

Influence of waves on the performance of ship power systems based on multi-physics fusion simulation model

College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China

基于多物理模型融合仿真的波浪对船舶动力系统加速性能的影响丁宇，采用知识共享署名4.0国际许可协议进行许可。

摘要

摘要:
目的
提出一种融合螺旋桨水动力特性与船用柴油机热力学特性的船舶动力系统融合仿真方法，旨在揭示波浪扰动对船舶动力系统性能的影响规律。
方法
通过构建SST k-ω湍流模型与流体体积（VOF）模型，分析自由液面高度对螺旋桨敞水特性的影响规律。采用基于Seiliger热力学循环的柴油机平均值模型模拟船舶主机稳态和动态运行过程，得到主机热力学参数及其变化规律。基于动力系统融合模型，研究波浪环境下船舶加速过程中动力系统的动态响应特性。
结果
结果显示，风浪工况会改变螺旋桨淹没的深度，导致螺旋桨推力最大损失18.34%，影响了螺旋桨推力输出的稳定性与船舶运行安全性；船舶主机在加速过程中，排气温度和过量的空气系数受波浪扰动会产生剧烈波动，最大值分别达1 370 K与0.558 9，超过了主机的安全运行边界。
结论
所提方法通过融合螺旋桨水动力模型与柴油机热力学模型，可准确预测波浪环境下船舶动力系统动态性能的变化规律，揭示螺旋桨水动力参数与主机热力学参数的耦合响应特性，再结合船舶主机运行边界分析，可为船舶动力系统在极端海况下的控制策略研究提供理论支撑。
- 船舶动力系统 /
- 波浪 /
- 螺旋桨水动力 /
- 船舶主机 /
- 多物理融合模型
Abstract:
Objectives
This study proposes an integrated simulation method for marine power systems combining propeller hydrodynamic characteristics with diesel engine thermodynamic properties, aiming to reveal the influence of wave disturbances on system performance.
Methods
The SST k-ω turbulence model and volume of fluid (VOF) method were employed to analyze free surface effects on propeller open-water characteristics. A Seiliger-cycle-based mean-value engine model simulated steady/dynamic operations of the main engine, obtaining thermodynamic parameters. The integrated power system model investigated dynamic responses during ship acceleration in waves.
Results
Under wave conditions, alterations in propeller immersion depth result in a maximum thrust reduction of 18.34%. This reduction affects the stability of propeller thrust output and poses a threat to the operational safety of the vessel. During the acceleration phase of the ship's main engine, exhaust temperature and excess air ratio fluctuate significantly due to wave disturbances, reaching maximum values of 1 370 K and 0.558 9, respectively. These values exceed the safe operational limits for the main engine. Consequently, measures must be implemented to alleviate the impact of waves on the main engine's performance to ensure the safety and efficiency of the ship's operation.
Conclusions
The proposed method accurately predicts dynamic performance variations in waves by coupling hydrodynamic and thermodynamic models, revealing parameter interaction mechanisms. Combined with operational boundary analysis, it provides theoretical support for developing control strategies under extreme sea conditions.
- ship propulsion system /
- wave /
- propeller hydrodynamic /
- marine engines /
- multi-physics co-simulation

HTML全文

0. 引　言

海上航运承担了全球商品贸易运输总量的80%～90%^[1]。受海洋环境多变的困扰，在极端天气和海况的影响下，远洋船舶动力系统负载变化剧烈，会导致运行的安全性降低，故障发生率增加^[2]。海浪与船舶推进器直接作用易导致船舶动力系统负载波动，对系统的影响尤为严重^[3]，进一步加重了安全隐患。因此，在波浪的影响下，螺旋桨的水动力性能变化与船舶主机内部热力学性能的变化将成为研究船舶在极端条件下运行安全性的重点。为进一步研究波浪环境对船舶动力系统的影响，本文将融合螺旋桨水动力模型船舶主机热力学模型，模拟并分析波浪状态下螺旋桨和船舶主机的各项参数，为动力系统在风浪条件下的控制策略提供研究基础。

计算风浪影响下螺旋桨的水动力性能变化主要有2种方法，即基于物理原理建模的计算方法和经验公式估算法。为减少船舶动力系统仿真中的计算量，并能够仿真波浪工况下船舶动力系统各设备的运行规律，经验公式法被广泛应用于螺旋桨水动力性能预测。Sui等^[4]在动力系统模型中使用经验公式法估算了波浪对船体产生的漂移力以及波浪对螺旋桨伴流分数的影响。Ma等^[5]在电力动力系统中使用经验公式法对螺旋桨发生卷吸时的情况进行了建模，该模型能够模拟不同卷吸状态下螺旋桨敞水特性的变化规律。然而，经验公式在一定程度上对螺旋桨周围流场的复杂作用进行了简化，无法获取螺旋桨周围流场的特征，适用范围存在局限性。使用详细的CFD模型能够获得螺旋桨周围流场以及螺旋桨的水动力学特性，开展螺旋桨尾流受自由液面影响而产生的卷吸现象研究，能够进一步确定淹深、波浪流向和波浪频率对螺旋桨水动力特性的影响规律^[6–9]。但是，在CFD模型的动态计算过程中会产生大量的冗余数据，难以适应船舶动力系统的仿真步长，导致仿真时间增加，计算资源浪费。

船舶动力系统中，主机常用的建模方法有三维建模方法、准维建模方法、零维建模方法及拟合模型等^[10]。在主机工作过程中，燃烧过程最为复杂，其建模方法决定了整机模型的计算时间以及精度。采用三维方法、准维方法和零维方法的燃烧模型均是以柴油机单位曲柄转角为时间步长，能够不同程度地模拟发动机内部燃烧过程中工质压力和温度的变化规律^[11–14]，但这些建模方法也导致模型仿真时间增加，难以与动力系统模型结合。拟合模型主要用于监测发动机的油耗和排放数据^[15]，难以反映发动机工作过程中内部热力学参数的变化规律。而船用主机平均值模型在原理模型的基础上，采用Seiliger热力学循环可进一步简化燃烧模型，其使用5-6采样点模拟缸内温度和压力变化，能够大幅降低所需计算资源，精确捕捉柴油机缸内关键信息，使该模型能够在输出主机关键热力学参数的同时满足动力系统模型的运行需求^[16]。

针对上述提出的问题与不足，本文拟采用CFD方法模拟自由液面高度对螺旋桨敞水特性的影响，并与基于Seiliger热力学循环的船用平均值模型进行离线仿真，研究不同工况下发动机内部热力学参数的变化规律。随后，建立融合了螺旋桨水动力模型与船舶主机热力学模型的船舶动力系统模型，仿真分析船舶动力系统在波浪中的加速工况。得到波浪影响状态下船舶动力系统特性参数的变化范围，为动力系统安全性分析提供基础。

1. 螺旋桨水动力模型建立

为简化波浪对螺旋桨的影响，选择使用自由液面高度来表征波浪在其波峰、波谷上的相位。自由液面影响下的螺旋桨水动力性能使用STAR CCM+软件进行求解，该软件被广泛应用于船海领域的CFD研究^[17]。本文拟针对一艘38 800 DWT散货船的螺旋桨进行仿真研究，螺旋桨直径6.4 m，模型缩尺比1∶24，盘面比0.43，螺距比0.734，为三叶螺旋桨。为换算桨模与实际螺旋桨之间的推力，使用无量纲化推力和扭矩系数表征模型尺度螺旋桨的水动力性能，如式（1）和式（2）所示。

$K_{T}=T /\left(\rho \cdot n^{2}\cdot D^{4}\right)$

(1)

$K_{Q}=Q /\left(\rho\cdot n^{2}\cdot D^{5}\right)$

(2)

式中：K_T，K_Q分别为无量纲化的螺旋桨推力和扭矩系数；T，Q分别为螺旋桨推力和扭矩；ρ为螺旋桨工作环境液体密度；n为螺旋桨转速；D为螺旋桨直径。

1.1 数值方法

本文采用STAR CCM+中的SST k-ω（RANS）模型对螺旋桨流场黏性湍流控制方程进行求解。基于不可压缩流体假设，流体满足动量守恒方程与质量守恒方程，如式（3）和式（4）所示。

$\begin{split} & \quad\frac{{\partial (\rho \cdot {u_i})}}{{\partial t}} + \frac{{\partial (\rho \cdot {u_i} \cdot {u_j})}}{{\partial {x_j}}} = \\& - \frac{{\partial p}}{{\partial x}} + \frac{\partial }{{\partial {x_j}}}(\mu \cdot \frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \overline {u_i' \cdot u_j'} ) \end{split}$

(3)

$\frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} = 0$

(4)

式中： $-\rho \overline{u_{i}' u_{j}'}$ 为雷诺应力项u_i，u_j 分别为不同方向上的速度分量；x，x_i，x_j 分别为该物理量对应的空间坐标；μ为动力粘度系数；p为时均压力；t为时间。

使用静水流体体积（VOF）波模型模拟静水中的自由液面影响，VOF分数满足以下方程：Grid independence verification for open-water propeller

$\frac{{\partial F}}{{\partial t}} + \frac{{\partial \left( {F{U_i}} \right)}}{{\partial {x_i}}} = 0$

(5)

式中：F为流体体积分数，F = 0表示计算域内充满轻流体（空气），F = 1表示计算域内充满重流体（水）；U_i为该方向上的速度分量。

1.2 计算域与网格划分

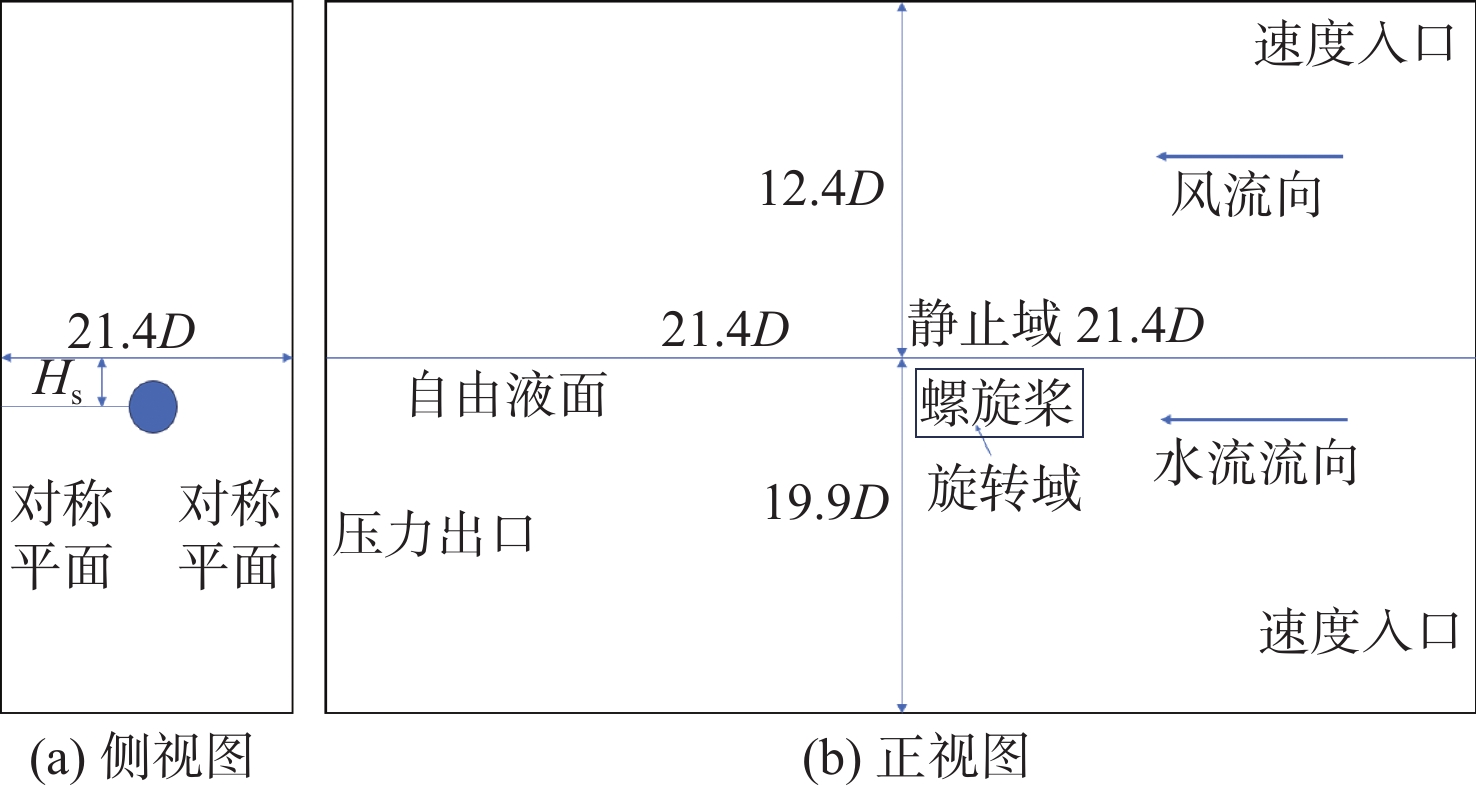
计算域为长方体模拟水池，其边界条件以及尺寸设置如图1所示，其中图1（a）为计算域侧视图，图1（b）为计算域正视图。本文采用RBM（rigid body motion）运动模型，计算域分为静止域与旋转域，其中静止域用于模拟试验水池环境，旋转域用于模拟螺旋桨的旋转运动，旋转域与静止域交界处设置为交界面。图中：H_s为淹深；蓝色实心圆为旋转域，该旋转域直径1.2D，长度1.5D；其余部分则为静止域。

图 1 螺旋桨计算域划分

Figure 1. Division of propeller computational domain

下载: 全尺寸图片幻灯片

计算域的划分原则为：在节约计算资源的前提下扩大计算域，避免虚拟水池壁对螺旋桨周围流场产生影响。仿真中，通过控制H_s的大小来决定螺旋桨轴系的淹深，以及自由液面对螺旋桨产生的影响。

静止域采用STAR CCM+中的切割体网格生成器，旋转域采用多面体网格生成器进行网格生成，网格基础尺寸设置为0.4D（中等）、0.8D（粗糙）和0.2D（精细）。为满足SST k-ω模型要求，使用棱柱层网格，保证近壁面y⁺≈1，棱柱层设置为15层，总厚度0.4 mm，增长率1.3。网格场景如图2所示，其中VOF波采用切割体网格各向异性加密方法，垂直方向设置40层网格加密自由液面区域，用以捕捉自由液面对螺旋桨尾涡的影响。

图 2 计算域截面网格场景

Figure 2. Cross-section mesh of the computational domain

下载: 全尺寸图片幻灯片

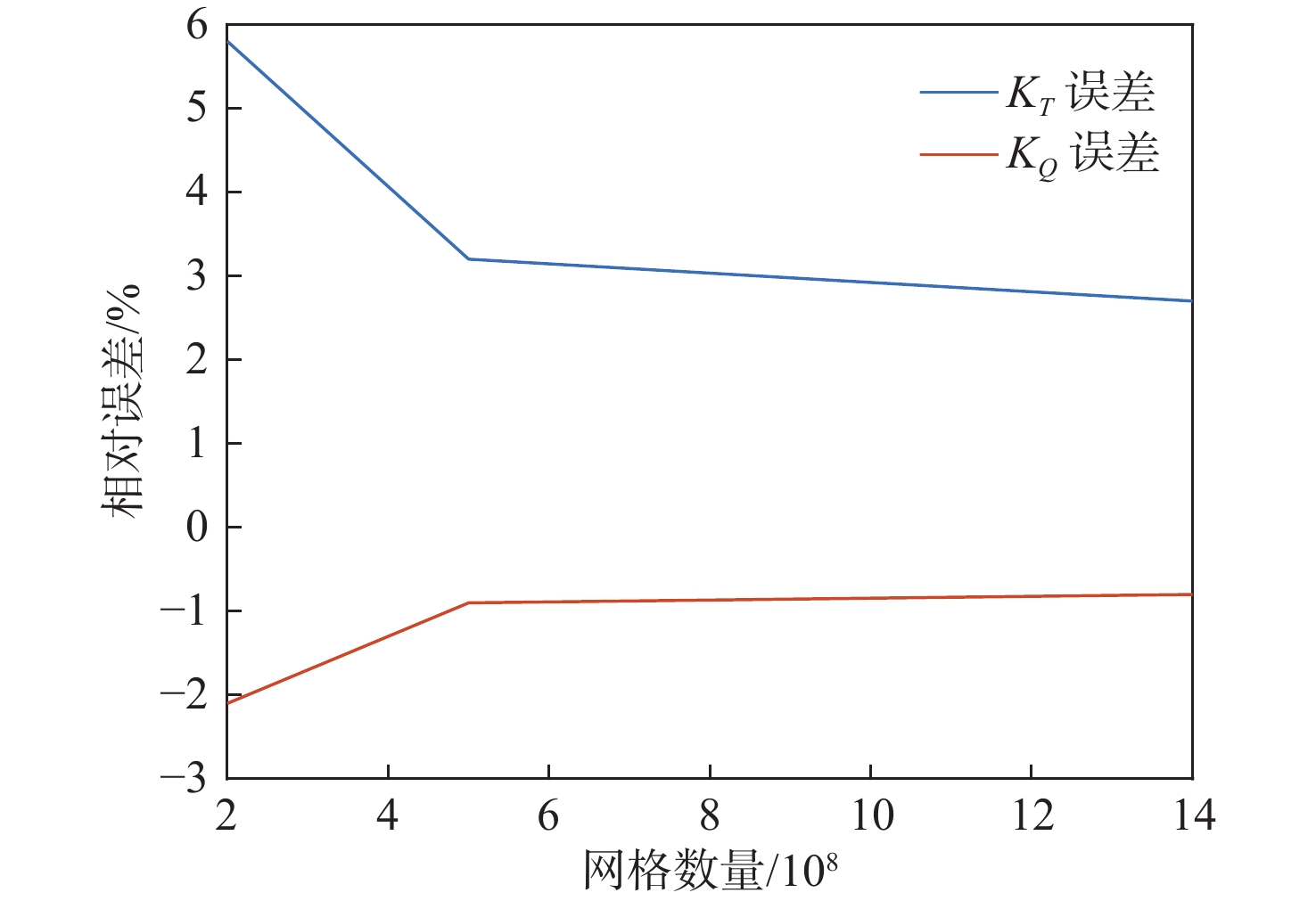
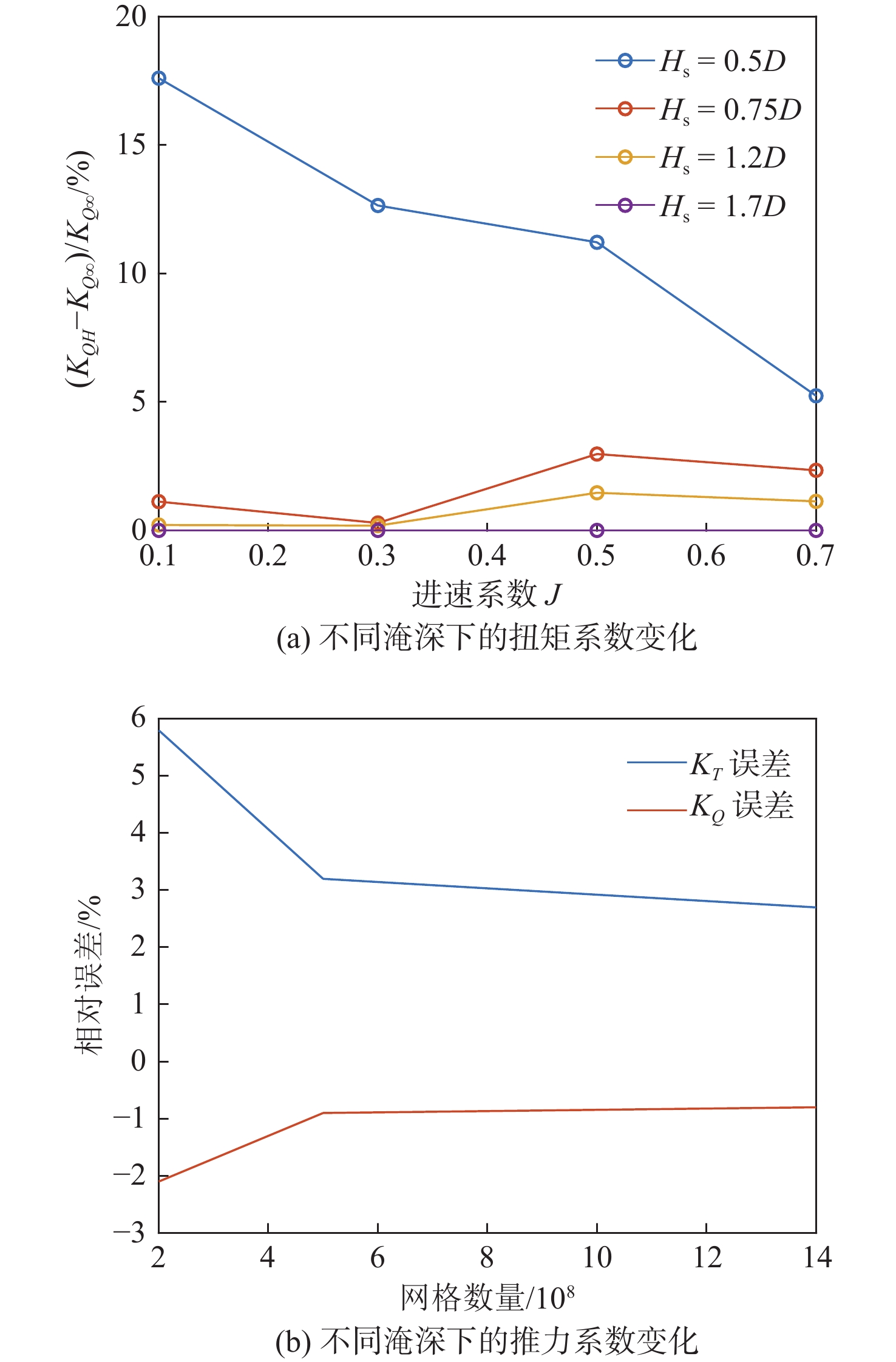
对比3套网格计算结果（表1），可知中等网格能够在占用较少计算资源的情况下得到较为准确的结果，且如图3所示，螺旋桨敞水计算结果随着网格数量的增加，其误差逐渐减小并趋于稳定，可以推测当网格数量进一步增加时，螺旋桨敞水特性变化量将越来越小，并在网格无穷多时达到稳定值。本文选择中等网格进行后续计算。

表 1 螺旋桨敞水网格无关性验证（J = 0.3，物理时间1 s）

Table 1. Mesh independence verification for open water propeller (J = 0.3，physic time=1 s)

组别	K_T误差/%	K_Q误差/%	网格数量	计算时间/ h
粗糙网格	5.8	−2.1	2×10⁶	6
中等网格	3.2	−0.9	5×10⁶	12
精细网格	2.7	−0.8	14×10⁶	30

下载: 导出CSV

| 显示表格

图 3 网格无关性验证

Figure 3. Mesh independence verification

下载: 全尺寸图片幻灯片

$K_{{T}}误差=\frac{(K_{{T,}\mathrm{EFD}}-K_{{T,}\mathrm{CFD}})}{K_{{T,}\mathrm{EFD}}}$

(6)

$K_{{Q}}误差=\frac{(K_{{Q,}\mathrm{EFD}}-K_{{Q,}\mathrm{CFD}})}{K_{{Q,}\mathrm{EFD}}}$

(7)

式中：K_TCFD，K_TEFD 分别为敞水计算与水池试验所得推力系数；K_QCFD，K_QEFD 分别为敞水计算与水池试验所得扭矩系数。

1.3 模型验证

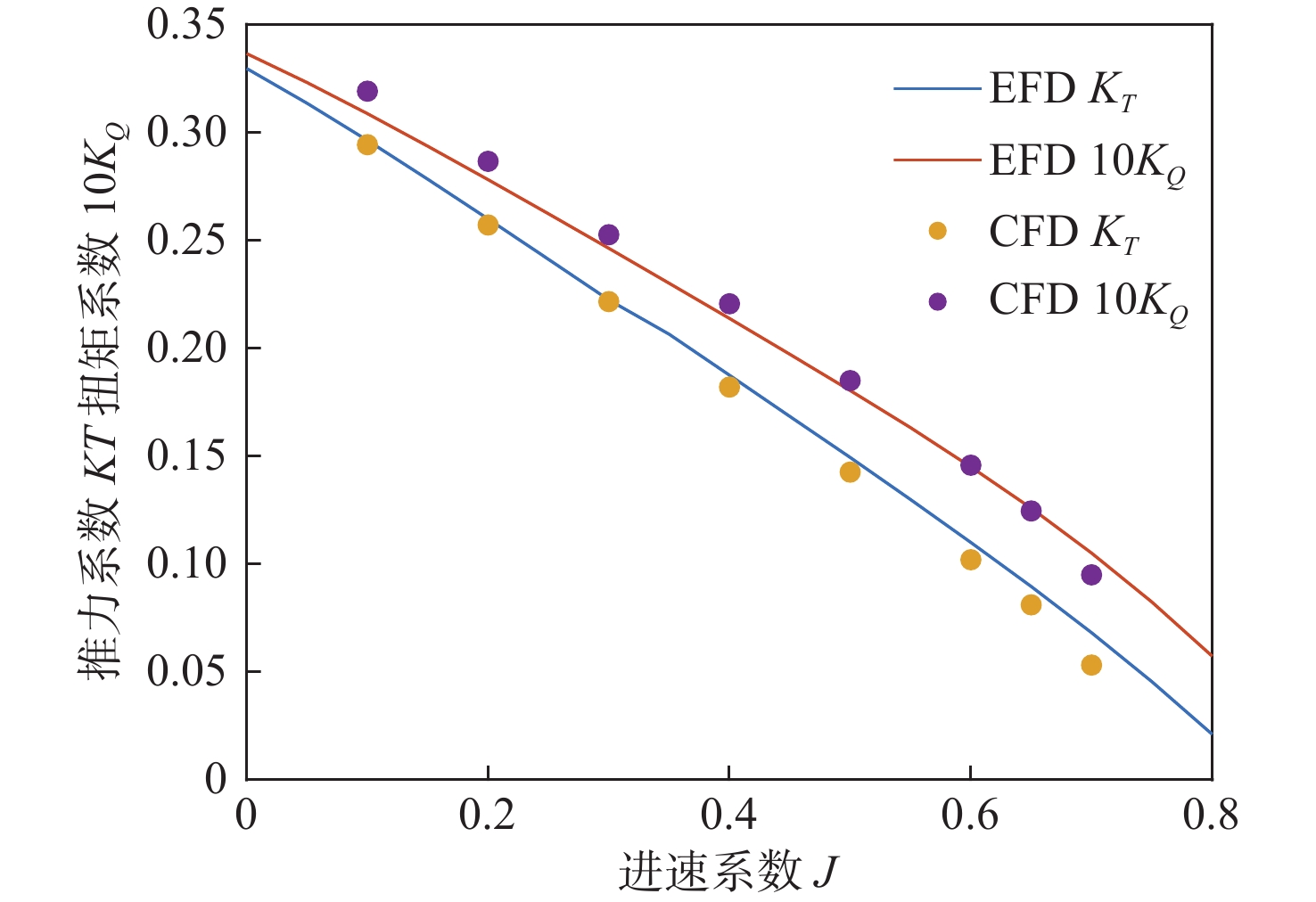
为了验证模型的准确性，将螺旋桨敞水CFD结果与桨模拖曳试验结果进行了对比，结果如图4所示，其中CFD表示计算结果，EFD表示水池试验结果^[18]。常用进速系数（J = 0.3～0.6）下推力系数与扭矩系数的误差均在5%以内，可以满足计算要求，其中大进速系数状态下的误差偏大，其原因是在大进速系数下推力较小且易发生复杂的湍流现象，总体推力与扭矩变化趋势符合螺旋桨的运行规律。因此，该螺旋桨CFD模型的精度能够满足后续的研究需求。

图 4 螺旋桨敞水特性验证

Figure 4. Validation of propeller open water characteristic

下载: 全尺寸图片幻灯片

1.4 数值计算结果分析

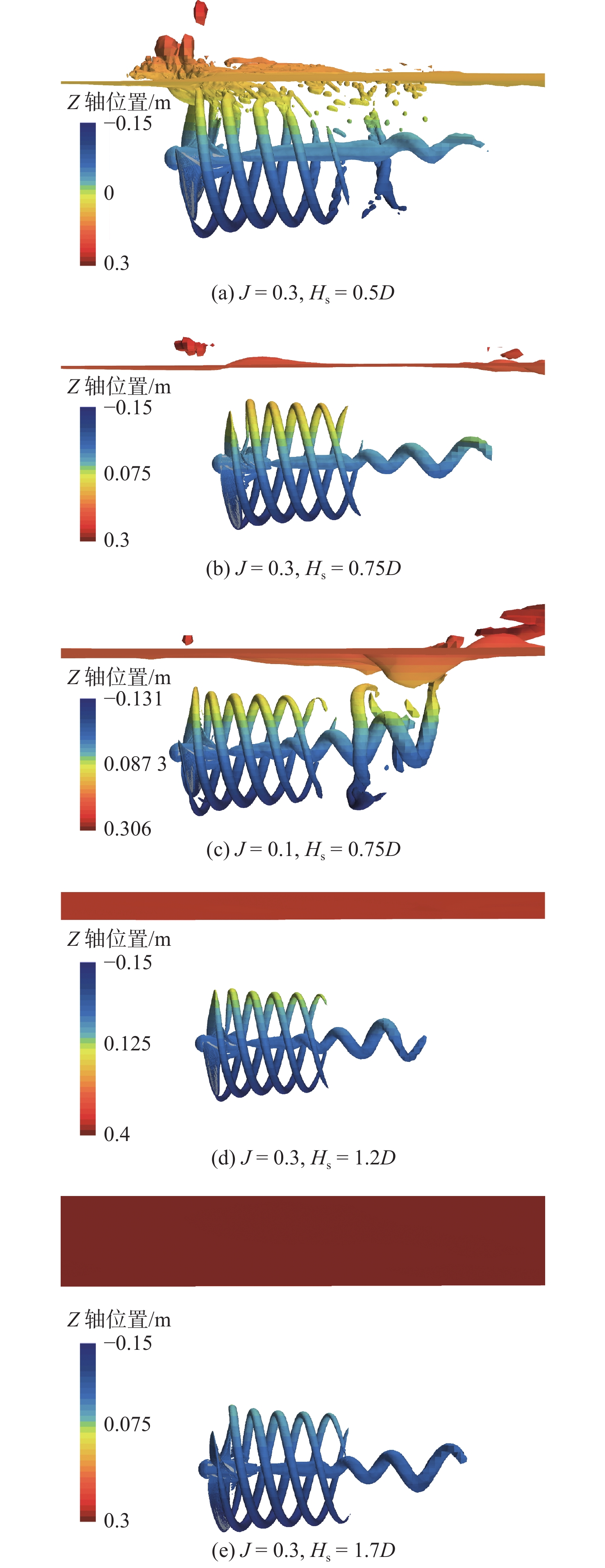
如图5所示，螺旋桨尾部流场在螺旋桨的作用下产生了显著的涡量分布，该涡量可通过Q准则函数进行捕捉分析。由图5（a）和图5（b）可知，当螺旋桨靠近自由液面时，其尾流受自由液面的影响逐渐增强，并引发卷吸现象。由图5（b）和图5（c）可知，螺旋桨在低进速系数工况下受自由液面的影响更为显著，这是因为在低进速系数下，螺旋桨的推力较大，叶背压力会升高，更容易扰动自由液面，从而引发卷吸现象。发生卷吸现象后，螺旋桨推力系数和扭矩系数均会受到影响，将表现为不同程度的下降（图6 ）。在卷吸状态下，自由液面上的空气会被卷入螺旋桨尾流，从而改变流场结构，影响螺旋桨的水动力性能。相较之下，当螺旋桨远离自由液面时，如图5（d）和图5（e）所示，受到自由液面的影响非常小，尾涡能够自由展开。当淹深H_s >1.2D时，卷吸影响可以忽略不记。图6对比了不同淹深下螺旋桨的敞水特性，结果显示当H_s从1.2D增加至1.7D时，螺旋桨推力和扭矩系数的变化量小于1%。因此，当H_s >1.2D时，自由液面对螺旋桨水动力性能的影响极小，螺旋桨可视为在近无限水深条件下运行。在卷吸状态下，螺旋桨推力与扭矩随桨叶的旋转呈周期性波动。为准确评估该工况下的水动力特性，本文采用一个旋转周期内的推力系数和扭矩系数的平均值来表征螺旋桨的敞水特性，这一方法能够有效减少瞬时扰动对数据分析的影响，提高计算结果的可靠性。

图 5 自由液面对螺旋桨尾流场的影响

Figure 5. Influence of free surface on propeller tail flow

下载: 全尺寸图片幻灯片

图 6 不同淹深对螺旋桨运行特性的影响

Figure 6. Influence of various depth of propeller axis on propeller characteristic

下载: 全尺寸图片幻灯片

由图6可以看出，螺旋桨推力和扭矩系数随着轴系淹深的减小出现了下降趋势，当螺旋桨发生严重的卷吸时（H_s = 0.5D），推力和扭矩系数大幅下降，分别为18.34%和17.5%。对比H_s = 0.5D时不同进速系数下的曲线，发现推力和扭矩系数的下降幅度随进速系数的减小增加。当轴系淹深H_s = 0.75D时，螺旋桨受自由液面的影响减小，螺旋桨推力扭矩特性轻度下降，下降幅度均在5%以内。当轴系淹深H_s继续增加至1.2D 时，螺旋桨几乎不再受到自由液面的影响。当H_s < 0.5D时，螺旋桨部分露出水面，此时，需针对该工况进一步细化网格，并设置相应的求解条件^[19]。但是，因本文后续的计算并未涉及螺旋桨的出水问题，故对此情况不做详细分析。

2. 船舶动力系统模型建立

2.1 目标船舶动力系统结构

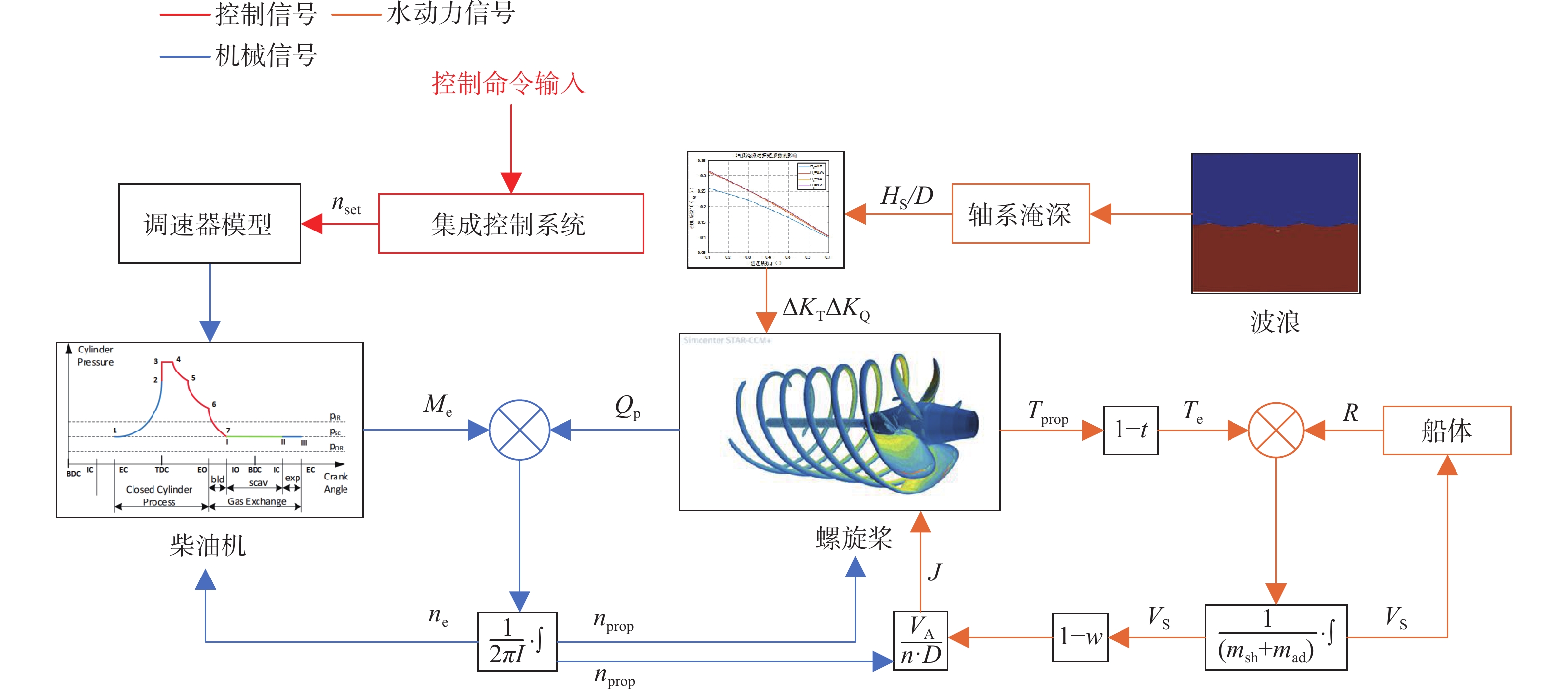
目标船舶的动力系统是主机−轴系−螺旋桨的机械传动方式，主机为WinGD 5X52型低速柴油机，系统基本参数如表2所示。根据主机−螺旋桨−船体的平衡关系与相互作用原理，建立船舶动力系统仿真模型结构如图7所示。图中：n_set为主机调速器设定转速；n_e为发动机实际转速；n_prop为螺旋桨转速；M_e为主机输出扭矩；Q_p为螺旋桨扭矩；T_e为船舶有效推力；T_prop螺旋桨输出推力；V_A为螺旋桨进速；w为螺旋桨伴流分数。

表 2 38 800 DWT散货船动力系统基本参数

Table 2. Basic parameters of propulsion system of 38 800 DWT bulk carrier

参数		数值
螺旋桨	桨直径/m	6.4
	桨叶数	3
	螺距比	0.734
船体	设计水线长/m	179.95
船体	设计排水量/t	43 503
主机	额定功率/kW	6 408
	额定转速/(r ∙ min⁻¹)	99
	缸径/m	0.52
	气缸数	5

下载: 导出CSV

| 显示表格

图 7 船舶动力系统仿真模型结构

Figure 7. Structure of ship propulsion system

下载: 全尺寸图片幻灯片

其中船舶主机−螺旋桨满足转动如式（8）所示的平衡方程。

$2{\text{π}} \cdot I \cdot \frac{{{\mathrm{d}}n}}{{{\mathrm{d}}t}} = {M_{\mathrm{E}}} - {Q_{\mathrm{P}}}$

(8)

式中：I为轴系以及螺旋桨的转动惯量；n为主机及螺旋桨转速；M_E，Q_P分别为主机输出扭矩和螺旋桨扭矩。

螺旋桨与船体之间满足推力平衡方程，如式（9）所示。

$({m_{\rm{sh} }} + {m_{\rm{ad} }})\frac{{{\mathrm{d}}{V_S}}}{{{\mathrm{d}}t}} = T - R$

(9)

式中：m_sh为船体质量；m_ad为船舶运动附加质量；V_s为船舶航速；T为螺旋桨产生推力；R为船舶航行阻力。根据38 800 DWT散货船自航试验报告^[18]，确定伴流分数为0.342，推力减额分数为0.21。

根据图6所示的水动力仿真结果，使用样条插值函数，建立螺旋桨进速系数和淹深与螺旋桨推力、扭矩系数之间的函数关系，如式（10）和式（11）所示。

${K_T} = f({H_{\rm{s}} },J)$

(10)

${K_Q} = f({H_{\rm{s}} },J)$

(11)

在船体阻力模型中，静水阻力参考目标船舶试航报告中提供的R-V_s曲线^[20]。船舶在波浪中运行时，船舶阻力会随波浪周期性变化，波浪中阻力系数的大小由波浪增阻系数σ_aw表示，如式（12）所示。

${\sigma _{\rm{aw}}} = \frac{{\overline {{R_{\rm{wave}}}} - {R_{\rm{calm}}}}}{{\rho \cdot g \cdot \dfrac{{{B^2}}}{L} \cdot \zeta _A^2}}$

(12)

式中： $\overline {{R_{\rm{wave}}}}$ 为波浪中单一周期内船舶的阻力平均值；R_calm为船舶在静水中的阻力；B为船宽；L为船体垂线间长； $\zeta _A^{}$ 为试验波高。

由于船舶惯性远大于螺旋桨，其产生的动态响应频率低于螺旋桨的影响，故本文忽略船舶阻力波动值，取其平均波浪增阻系数作为本文波浪增阻的计算输入，通过参照其他运输类船舶CFD计算结果^[21-22]，再结合本文设置的波浪等级，计算得到增阻系数为2.3，波浪增阻为原船1.5倍左右。

2.2 主机平均值模型构建与验证

柴油机平均值模型包括进排气模型、中冷器、涡轮机模型和缸内模型等，其中缸内过程使用Seiliger循环^[23]，该过程可简化为5个热力学过程，分别为1-2多变压缩阶段，2-3等容燃烧阶段，3-4等压燃烧阶段，4-5等温放热阶段，5-6多变膨胀阶段，各过程的计算公式如表3所示。表中：r_c，r_e分别为多变过程的压缩/膨胀比；n_comp，n_exp分别为2个多变过程的绝热指数；a，b，c为Seiliger过程中燃烧阶段的3个seiliger参数。换气过程采用双区域扫气模型^[16]，假设缸内区域分为燃烧废气区域与新鲜空气区域，并进行相关的热力学计算。

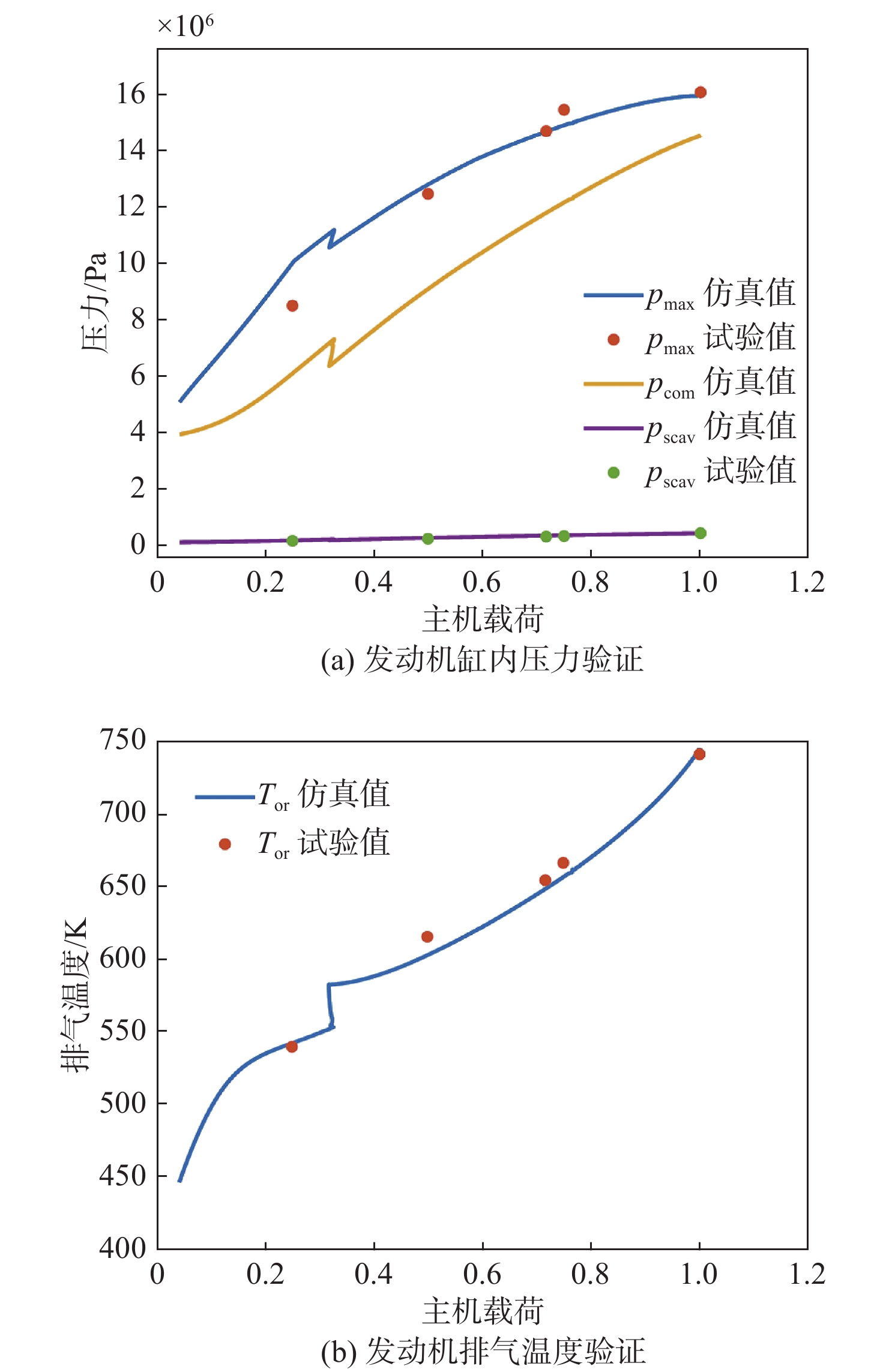
表 3 Seiliger 参数计算公式

Table 3. Calculation equations of Seiliger parameters

Seiliger过程	缸内体积V	缸内压力p	缸内温度T	Seiliger参数
1-2	$\dfrac{V_{1}}{V_{2}}=r_{e}$	$\dfrac{p_{2}}{p_{1}}=r_{c}^{n_{\rm{comp}}}$	$\dfrac{T_{2}}{T_{1}}=r_{c}^{n_{\rm{comp}}-1}$	$r_{c}, n_{\rm{comp}}$
2-3	$\dfrac{V_{3}}{V_{2}}=1$	$\dfrac{p_{3}}{p_{2}}=a$	$\dfrac{T_{3}}{T_{2}}=a$	a
3-4	$\dfrac{V_{4}}{V_{3}}=b$	$\dfrac{p_{4}}{p_{3}}=1$	$\dfrac{T_{4}}{T_{3}}=b$	b
4-5	$\dfrac{V_{5}}{V_{4}}=c$	$\dfrac{p_{4}}{p_{5}}=c$	$\dfrac{T_{5}}{T_{4}}=1$	c
5-6	$\dfrac{V_{6}}{V_{5}}=r_{e}$	$\dfrac{p_{5}}{p_{6}}=r_{e}^{n_{\rm{exp}}}=0$	$\dfrac{T_{6}}{T_{5}}=r_{e}^{1-n_{\rm{exp}}}$	$r_{e} n_{\text {exp}}$

下载: 导出CSV

| 显示表格

为了验证船舶主机平均值模型的准确性，对发动机缸内最高压力和涡前温度进行了验证，其分别表征发动机机械负荷与热负荷，是后续仿真中重要的特征参数，如图8所示。验证工况为24.8%，49.8%，71.6%，74.9%，100.1%的负载，其对应的转速分别为62，78.6，88.5，89.9，99 r/min。使用主机模型按照对应的工况点进行仿真，结果如图8所示。由图可知，爆发压力与压缩压力仿真结果间的误差均控制在5%以内，其中，低工况时误差较大（8%）。图中，为防止主涡轮低负荷时工作效率降低，在主机负荷约35%时开启了辅助涡轮增压器，导致压力与温度发生突变。总体来看，发动机涡后温度和压力等特性参数的变化趋势均符合发动机的运行规律，该模型的精度能够满足后续的仿真需求。

图 8 船舶主机平均值模型验证

Figure 8. Validation of ship main engine mean value model

下载: 全尺寸图片幻灯片

2.3 动力系统模型验证

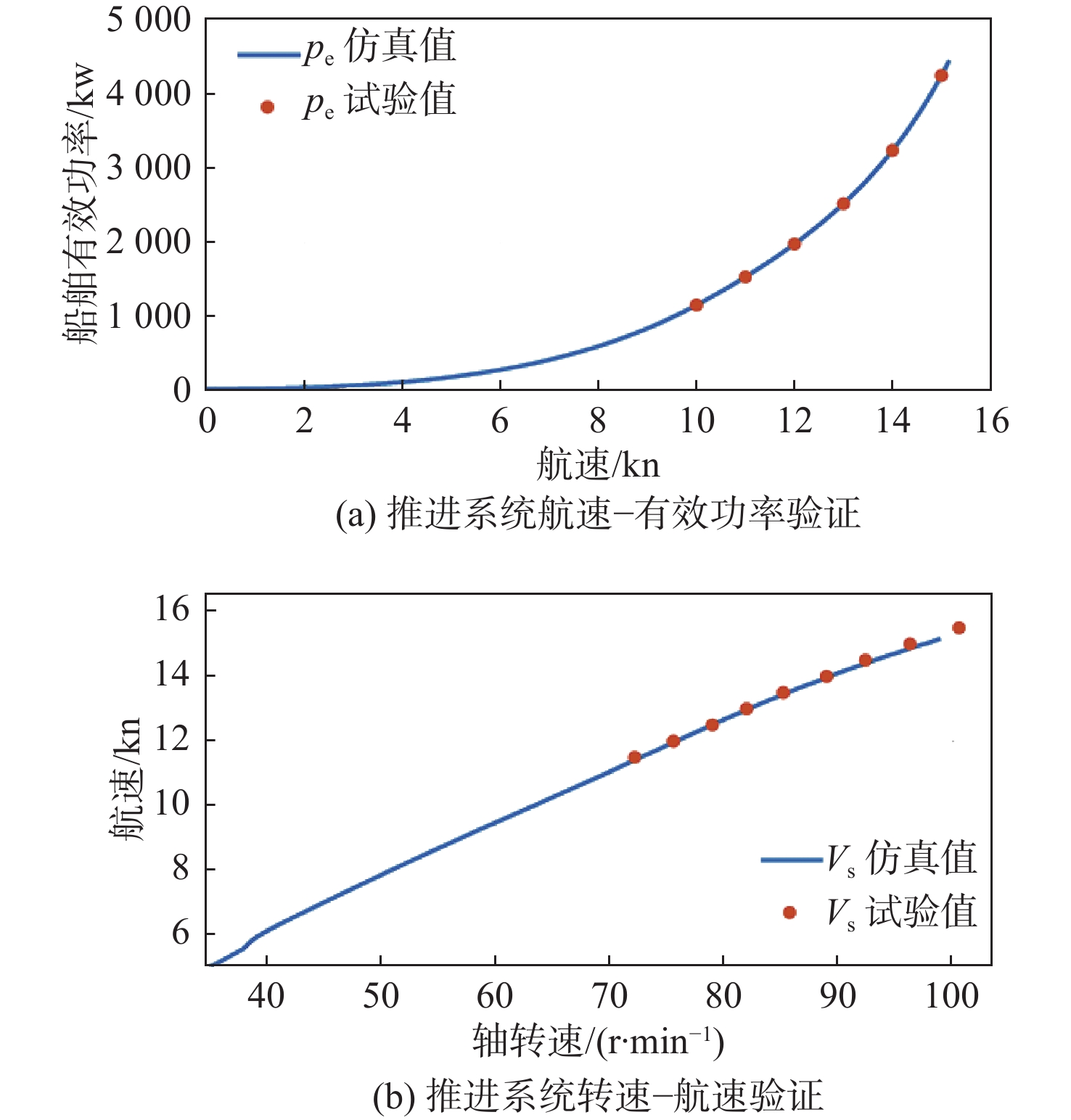
使用目标船舶试航报告数据对船舶动力系统模型进行验证，结果如图9所示。船舶有效功率（P_e-V_s曲线）和船舶航速（V_s-n曲线）的误差均在2%以内，能够满足工程需求。

图 9 船舶动力系统仿真模型验证

Figure 9. Ship propulsion system model validation

下载: 全尺寸图片幻灯片

3. 波浪影响下动力系统运行特性

将螺旋桨淹深变化下推力与扭矩的CFD计算模型与船舶柴油机平均值模型进行融合，研究船舶动力系统在风浪影响下加速工况的性能变化规律。分析波浪影响下船舶主机热力学参数的变化，以及对船舶加速性能的影响，进一步分析船舶动力系统在波浪工况下的运行安全。

3.1 波浪模型设置

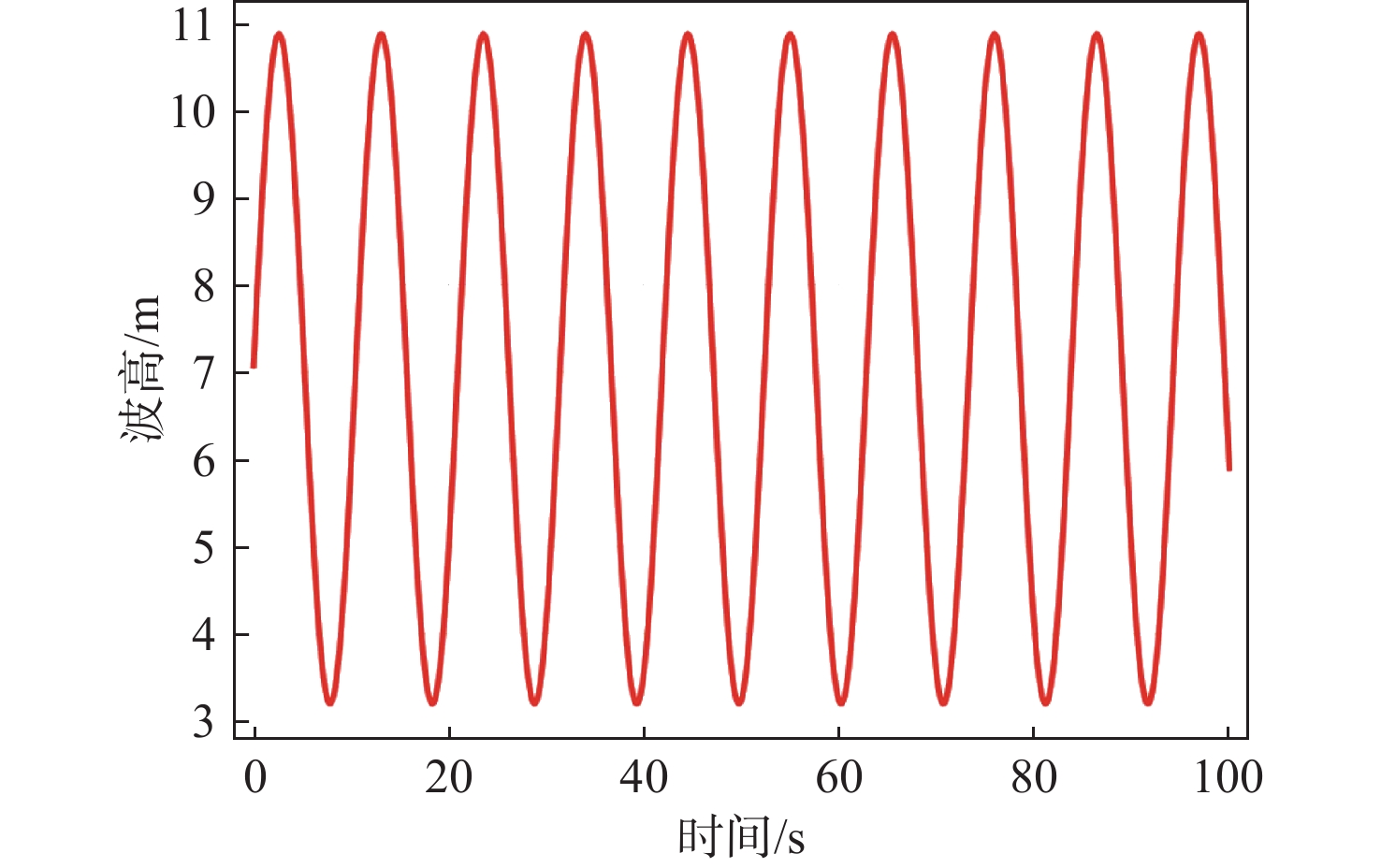
根据前文所述，当水面与螺旋桨桨轴之间的距离为1.2D时，螺旋桨受自由液面的影响可以忽略。因此，根据国家海洋局对浪高的定义^[24]，本节选择浪高为7级波浪，周期为12 s。

如图10所示，当波浪表面（自由液面）与螺旋桨桨轴的距离周期性波动（3.2～10.8 m）时，波峰与水平面之间的距离为0～7.6 m，符合7级波浪（H_1/3 = 6～9 m）的定义。图中，自由液面与桨轴的距离将作为动力系统中螺旋桨水动力特性计算模型的输入。

图 10 动力系统模型波高设置

Figure 10. Setting of wave height in propulsion system

下载: 全尺寸图片幻灯片

3.2 船舶动力系统加速工况性能分析

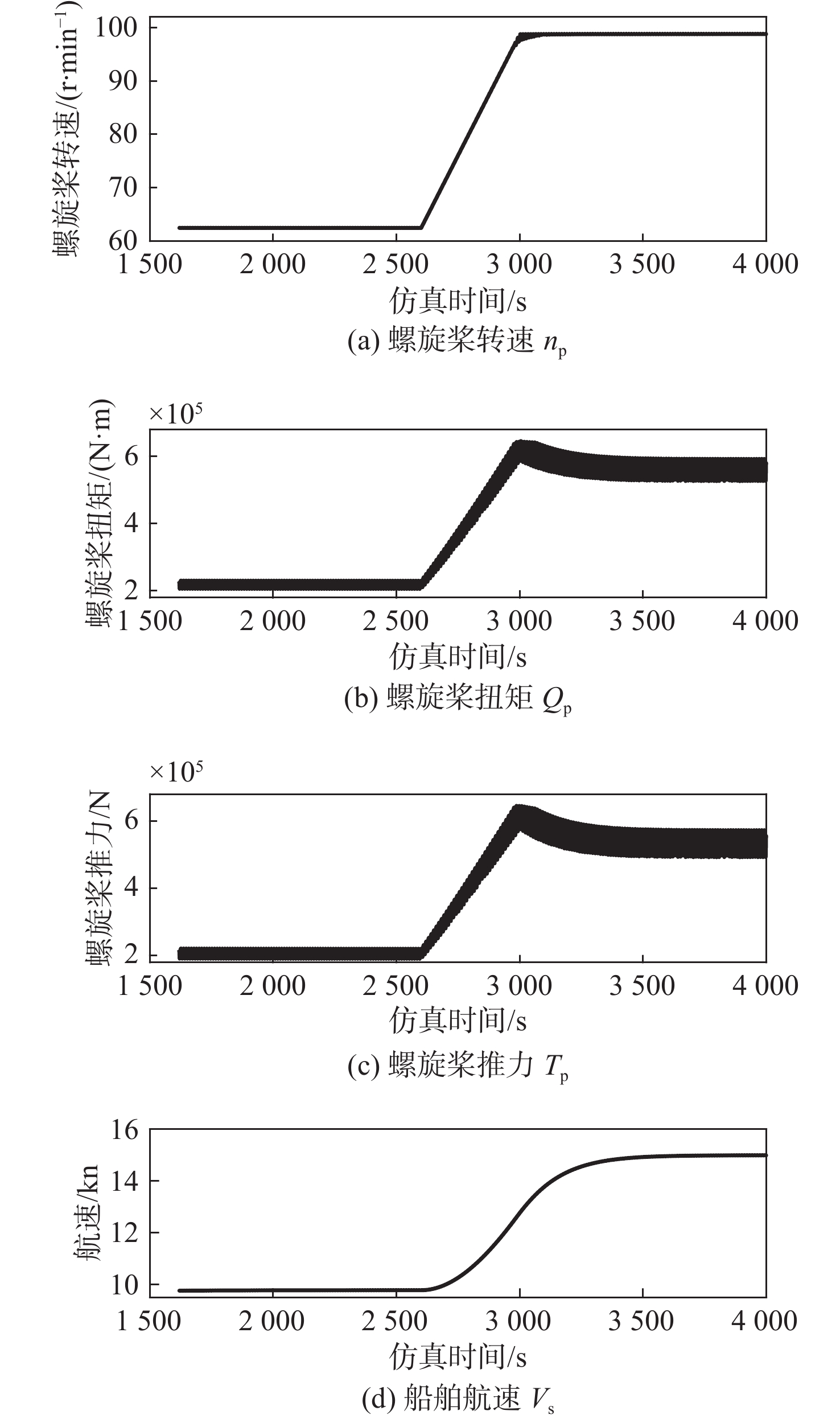
船舶动力系统采用PID策略调控主机的转速，在加速仿真过程中，柴油机调速器设定为400 s内由62.4 r/min加速至99 r/min，波浪对船体及螺旋桨的影响如图11所示。

图 11 加速工况下波浪对动力系统受的影响

Figure 11. Influence of wave conditions on the propulsion system under accelerating conditions

下载: 全尺寸图片幻灯片

如图11（a）所示，主机受调速器的调控在2 600 s处增加喷油量后转速得以提升。如图11（b）和图11（c）所示，随着螺旋桨转速的增加，螺旋桨扭矩和推力增加，并于3 000 s处停止增加，此时，螺旋桨负载达到最大。如图11（d）所示，在3 000 s处船速增加至12.8 kn，至3 500 s时船舶加速过程结束。在加速过程中，螺旋桨推力与扭矩由于波浪的作用，波动逐渐增加，波动值于加速至最大航速（4 000 s）时达到最大，推力的波动率为14.82%，扭矩的波动率为11.6%。由于惯性力的作用，螺旋桨转速与航速受影响较小，波动幅值均小于1%。螺旋桨推力和扭矩随着波浪的作用大幅波动，这样可能会导致船舶航行稳定性变差、轴系异常振动、空化增加等问题，且螺旋桨作为船舶主机负载，其剧烈波动会导致主机运行稳定性变差。因此，需进一步分析船舶主机运行特性受波浪的影响规律。

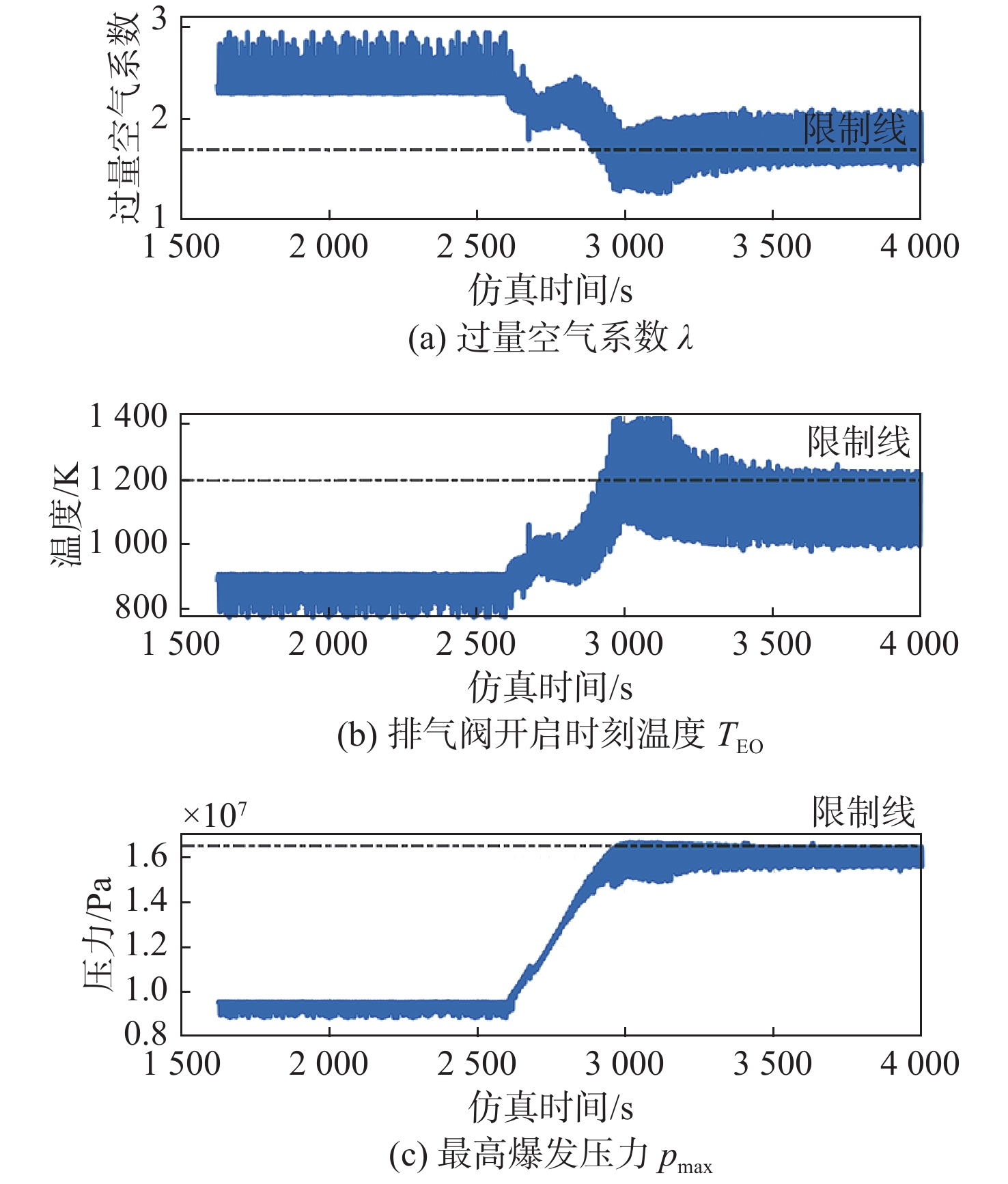
如图12（a）所示，主机加速在过程中，由于涡轮增压器的迟滞效应，导致在加速阶段（2 600～3 000 s）进气压力不足，过量空气系数降低。随着过量空气系数的进一步减小，在2 800 s处超出了柴油机的运行限制（λ = 1.7），由于主机负载的持续波动，导致船速稳定后过量空气系数仍然会超过柴油机的运行限制，导致柴油机燃烧不充分，产生黑烟等问题，加重了柴油机的热负荷。与过量空气系数类似，排气阀开启时刻的温度（图12（b））在仿真2 800 s时超出了运行边界（T_EO= 1 200 K），并于3 000 s时达到最大。排气阀开启时刻的缸内温度为主机缸内热负荷的重要指标，由于主机负载波动，导致加速稳定后其仍然超过了柴油机的运行限制，加重了主机的热负荷。图12（c）所示为船舶加速过程中主机最高爆发压力仿真结果。由图可见，由于加速导致的重载工况，主机的最高爆发压力有所增加，不过在加速过程结束后，爆发压力开始趋于稳定，且仅有小幅、短时超出了运行安全边界（p_max = 16.5 MPa），故不会对发动机运行安全产生影响。因此，在船舶加速过程中，主机爆发压力的变化相对可控，其影响程度较小。相较于柴油机的热负荷（例如，过量空气系数和排气阀开启时刻缸内温度），在加速过程中主机的机械负荷受影响较小，这表明在正常加速工况下，尽管爆发压力有所上升，但其对柴油机整体运行的影响相对有限，仍处于安全范围内。

图 12 加速工况下波浪对船舶主机的影响

Figure 12. Influence of wave conditions on marine engine performance under accelerating conditions

下载: 全尺寸图片幻灯片

图13所示为主机稳态运行限制区域，用于表征主机的热负荷和机械负荷等运行限制。当主机加速超过95 r/min时，由于负载波动加剧，主机进入超负荷运行限制区域，在此区域内长时间运行将会缩短主机的使用寿命，增加故障概率。

图 13 波浪影响下主机的负载路线

Figure 13. Marine engine loading trajectory under wave influence

下载: 全尺寸图片幻灯片

受螺旋桨负载波动以及由波浪所产生重载工况的影响，主机动态运行工况可能会超出其运行限制边界。在波浪环境下，当船舶处于加速工况时，其主机负载显著增加，可能接近甚至是超出主机的运行边界。主机的运行状态受功率−转速特性曲线的约束，在正常工作区域（绿色区域）内运行可确保动力系统的稳定性。然而，在波浪的作用下，主机负载的周期性变化使得主机负载发生剧烈的波动，导致其频繁接近或是超出运行限制线，甚至进入超负荷运行区域（红色区域）。当主机长期处于超负荷运行状态时，柴油机可能会因为过载而产生高温、高压等异常工况，增加关键部件（如活塞、曲轴及燃油喷射系统）的损耗，进而增加故障发生的概率。此外，超负荷运行还会降低燃油的经济性，导致单位功率输出的燃油消耗率（BSFC）上升，影响船舶的运营效率。为避免主机长期运行于高负荷或超负荷区域，应结合实时监测数据优化负载管理策略，例如通过自动控制系统调整燃油喷射量或优化航行速度，从而减少波浪引起的负载波动。此外，合理选择推进装置匹配参数，提高主机对波浪干扰的适应能力，也是保障船舶动力系统运行安全与稳定的关键。因此，在波浪条件下应格外关注加速过程中的主机热负荷和机械负荷参数波动，以更加严格的限制条件重新设定柴油机调速器的控制策略，适应涡轮机的动态响应特性，避免过量空气系数不足而出现“冒黑烟”等燃烧问题。

4. 结　论

本文基于螺旋桨CFD仿真计算与船舶主机平均值的融合模型，对波浪工况下船舶动力系统加速工况的动态特性进行了研究，主要得到以下结论：

1）通过采用SST k-ω 湍流模型与VOF波模型研究船用螺旋桨在不同轴系淹深下自由液面对螺旋桨运行特性的影响，发现当螺旋桨在水下时，受自由液面的影响，推力和扭矩系数最大可下降18.34%和17.5%，且当淹深超过1.2D 时，螺旋桨所受自由液面的影响可以忽略不计。

2）构建了融合螺旋桨水动力模型与主机热力学模型的船舶动力系统仿真方法，能够实时反映螺旋桨在波浪负载影响下船舶主机热力学参数的波动，从而监测其是否超出运行边界。

3）由波浪引起的主机负载波动会导致柴油机加速运行时超出运行边界，致使主机热负荷和机械负荷增加，其中在主机排气阀开启时刻缸内温度与主机过量空气系数将超出运行边界达17%，并且由于波浪波动的影响，还会导致其无法长时间稳定工作于额定工况。

图 1 螺旋桨计算域划分

Figure 1. Division of propeller computational domain

下载: 全尺寸图片幻灯片

图 2 计算域截面网格场景

Figure 2. Cross-section mesh of the computational domain

下载: 全尺寸图片幻灯片

图 3 网格无关性验证

Figure 3. Mesh independence verification

下载: 全尺寸图片幻灯片

图 4 螺旋桨敞水特性验证

Figure 4. Validation of propeller open water characteristic

下载: 全尺寸图片幻灯片

图 5 自由液面对螺旋桨尾流场的影响

Figure 5. Influence of free surface on propeller tail flow

下载: 全尺寸图片幻灯片

图 6 不同淹深对螺旋桨运行特性的影响

Figure 6. Influence of various depth of propeller axis on propeller characteristic

下载: 全尺寸图片幻灯片

图 7 船舶动力系统仿真模型结构

Figure 7. Structure of ship propulsion system

下载: 全尺寸图片幻灯片

图 8 船舶主机平均值模型验证

Figure 8. Validation of ship main engine mean value model

下载: 全尺寸图片幻灯片

图 9 船舶动力系统仿真模型验证

Figure 9. Ship propulsion system model validation

下载: 全尺寸图片幻灯片

图 10 动力系统模型波高设置

Figure 10. Setting of wave height in propulsion system

下载: 全尺寸图片幻灯片

图 11 加速工况下波浪对动力系统受的影响

Figure 11. Influence of wave conditions on the propulsion system under accelerating conditions

下载: 全尺寸图片幻灯片

图 12 加速工况下波浪对船舶主机的影响

Figure 12. Influence of wave conditions on marine engine performance under accelerating conditions

下载: 全尺寸图片幻灯片

图 13 波浪影响下主机的负载路线

Figure 13. Marine engine loading trajectory under wave influence

下载: 全尺寸图片幻灯片

表 1 螺旋桨敞水网格无关性验证（J = 0.3，物理时间1 s）

Table 1 Mesh independence verification for open water propeller (J = 0.3，physic time=1 s)

组别	K_T误差/%	K_Q误差/%	网格数量	计算时间/ h
粗糙网格	5.8	−2.1	2×10⁶	6
中等网格	3.2	−0.9	5×10⁶	12
精细网格	2.7	−0.8	14×10⁶	30

下载: 导出CSV

表 2 38 800 DWT散货船动力系统基本参数

Table 2 Basic parameters of propulsion system of 38 800 DWT bulk carrier

参数		数值
螺旋桨	桨直径/m	6.4
	桨叶数	3
	螺距比	0.734
船体	设计水线长/m	179.95
船体	设计排水量/t	43 503
主机	额定功率/kW	6 408
	额定转速/(r ∙ min⁻¹)	99
	缸径/m	0.52
	气缸数	5

下载: 导出CSV

表 3 Seiliger 参数计算公式

Table 3 Calculation equations of Seiliger parameters

Seiliger过程	缸内体积V	缸内压力p	缸内温度T	Seiliger参数
1-2	$\dfrac{V_{1}}{V_{2}}=r_{e}$	$\dfrac{p_{2}}{p_{1}}=r_{c}^{n_{\rm{comp}}}$	$\dfrac{T_{2}}{T_{1}}=r_{c}^{n_{\rm{comp}}-1}$	$r_{c}, n_{\rm{comp}}$
2-3	$\dfrac{V_{3}}{V_{2}}=1$	$\dfrac{p_{3}}{p_{2}}=a$	$\dfrac{T_{3}}{T_{2}}=a$	a
3-4	$\dfrac{V_{4}}{V_{3}}=b$	$\dfrac{p_{4}}{p_{3}}=1$	$\dfrac{T_{4}}{T_{3}}=b$	b
4-5	$\dfrac{V_{5}}{V_{4}}=c$	$\dfrac{p_{4}}{p_{5}}=c$	$\dfrac{T_{5}}{T_{4}}=1$	c
5-6	$\dfrac{V_{6}}{V_{5}}=r_{e}$	$\dfrac{p_{5}}{p_{6}}=r_{e}^{n_{\rm{exp}}}=0$	$\dfrac{T_{6}}{T_{5}}=r_{e}^{1-n_{\rm{exp}}}$	$r_{e} n_{\text {exp}}$

下载: 导出CSV

参考文献(24)

[1]	林书涵, 陶爱峰, 曹力玮, 等. 风涌浪夹角及其快速变化对船舶航行安全的影响[J]. 中国港湾建设, 2025, 45(1): 1–7. doi: 10.7640/zggwjs202501001 LIN S H, TAO A F, CAO L W, et al. The impact of intersection angle between wind waves and swells and its rapid changes on ship navigation safety[J]. China Harbour Engineering, 2025, 45(1): 1–7 (in Chinese). doi: 10.7640/zggwjs202501001
[2]	崔会强, 易文欣. 基于熵权-TOPSIS的测量船大风浪航行安全性评估[J]. 航海技术, 2023(6): 14–18. YI W X. Safety assessment for surveying vessel sailing in the heavy sea based on entropy weight-TOPSIS[J]. Marine Technology, 2023(6): 14–18 (in Chinese).
[3]	ACANFORA M, DE LUCA F, PIGAZZINI R, et al. An experimental study on the open water characteristics of a ship propeller in waves[J]. Applied Ocean Research, 2025, 154: 104331. doi: 10.1016/j.apor.2024.104331
[4]	SUI C, DE VOS P, HOPMAN H, et al. Effects of adverse sea conditions on propulsion and manoeuvring performance of low-powered ocean-going cargo ship[J]. Ocean Engineering, 2022, 254: 111348. doi: 10.1016/j.oceaneng.2022.111348
[5]	MA S P, DING Y, LIU G Z, et al. Predicting propeller emergence severity in adverse sea conditions: an integrated approach using stacked machine learning models[J]. Ocean Engineering, 2024, 303: 117811. doi: 10.1016/j.oceaneng.2024.117811
[6]	EOM M J, JANG Y H, PAIK K J. A study on the propeller open water performance due to immersion depth and regular wave[J]. Ocean Engineering, 2021, 219: 108265. doi: 10.1016/j.oceaneng.2020.108265
[7]	IRANNEZHAD M, KJELLBERG M, BENSOW R E, et al. Experimental and numerical investigations of propeller open water characteristics in calm water and regular head waves[J]. Ocean Engineering, 2024, 302: 117703. doi: 10.1016/j.oceaneng.2024.117703
[8]	胡学聪. 基于实际海浪大尺度模型试验的舰船航行性能综合评估[D]. 哈尔滨: 哈尔滨工程大学, 2020. doi: 10.27060/d.cnki.ghbcu.2020.000105. HU X C. Comprehensive evaluation of ship navigation performance based on large scale model test in actual ocean wave[D]. Harbin: Harbin Engineering University, 2020. doi: 10.27060/d.cnki.ghbcu.2020.000105 (in Chinese).
[9]	张耕, 姚建喜. 波浪中的螺旋桨水动力性能数值分析[J]. 上海交通大学学报, 2024, 58(2): 175–187. doi: 10.16183/j.cnki.jsjtu.2022.247 ZHANG G, YAO J X. Numerical analysis of hydrodynamic performance of propeller in waves[J]. Journal of Shanghai Jiaotong University, 2024, 58(2): 175–187 (in Chinese). doi: 10.16183/j.cnki.jsjtu.2022.247
[10]	张熠. 智能船舶低速主机的建模方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2019. ZHANG Y. Research on modelling method of low-speed main engine on intelligent ship[D]. Harbin: Harbin Engineering University, 2019 (in Chinese).
[11]	沈浩生, 张均东. 面向轮机模拟器的船用大型二冲程柴油机建模方法研究[D]. 大连: 大连海事大学, 2020. doi: 10.26989/d.cnki.gdlhu.2020.002016. SHEN H S, ZHANG J D. Research on the modeling method of marine large-scale two-stroke diesel engine oriented to marine engine room simulator[D]. Dalian: Dalian Maritime University, 2020. doi: 10.26989/d.cnki.gdlhu.2020.002016 (in Chinese).
[12]	何强, 陈丹, 杨城. 基于AVL-Boost船用二冲程柴油机性能优化仿真[J]. 舰船科学技术, 2022, 44(3): 101–106. doi: 10.3404/j.issn.1672-7649.2022.03.019 HE Q, CHEN D, YANG C. Marine two-stroke diesel engine performance optimal simulation based on AVL_BOOST[J]. Ship Science and Technology, 2022, 44(3): 101–106 (in Chinese). doi: 10.3404/j.issn.1672-7649.2022.03.019
[13]	付雪青, 张岩, 丁占铭, 等. 进排气压力对气门式二冲程柴油机扫气过程的影响[J]. 汽车安全与节能学报, 2023, 14(1): 125–132. doi: 10.3969/j.issn.1674-8484.2023.01.015 FU X Q, ZHANG Y, DING Z M, et al. Effects of intake and exhaust pressures on the scavenging process in a poppet-valved two-stroke diesel engine[J]. Journal of Automotive Safety and Energy, 2023, 14(1): 125–132 (in Chinese). doi: 10.3969/j.issn.1674-8484.2023.01.015
[14]	KARVOUNIS P, THEOTOKATOS G. Parametric optimisation of diesel–methanol injection timings of a dual-fuel marine engine operating with high methanol fraction using CFD[J]. Applied Thermal Engineering, 2025, 264: 125433. doi: 10.1016/j.applthermaleng.2025.125433
[15]	SANG Y J, DING Y, XU J R, et al. Ship voyage optimization based on fuel consumption under various operational conditions[J]. Fuel, 2023, 352: 129086. doi: 10.1016/j.fuel.2023.129086
[16]	SUI C B, DE VOS P, STAPERSMA D, et al. Mean value first principle engine model for predicting dynamic behaviour of two-stroke marine diesel engine in various ship propulsion operations[J]. International Journal of Naval Architecture and Ocean Engineering, 2022, 14: 100432. doi: 10.1016/j.ijnaoe.2021.100432
[17]	周伟新, 刘登成, 董郑庆, 等. STAR-CCM+船舶推进器水动力性能计算案例[M]. 哈尔滨: 哈尔滨工程大学出版社, 2021. ZHOU W X, LIU D C, DONG Z Q, et al. Case studies on hydrodynamic performance calculation of ship propulsors using STAR-CCM+[M]. Harbin: Harbin Engineering University Press, 2021 (in Chinese). (查阅网上资料, 未找到本条文献英文信息, 请确认)
[18]	ZENG F, HUANG L. The sea trial measurement report for "Great Intelligence": JJZH171109A1[R]. Shanghai: CSSC Huangpu Wenchong Shipbuilding Co. , Ltd. , 2017. (查阅网上资料, 未找到本条文献信息, 请确认)
[19]	史宗鹰. 面向强动态载荷的半浸桨集成设计计算方法[D]. 北京: 中国舰船研究院, 2023. doi: 10.27798/d.cnki.gzgjc.2023.000003. SHI Z Y. Integrated design and calculation method based on strong dynamic load of the partially submerged propeller[D]. Beijing: China Ship Scientific Research Center, 2023. doi: 10.27798/d.cnki.gzgjc.2023.000003 (in Chinese).
[20]	TAN Q, DING Y, LIU J C, et al. CFD-based hull-engine-propeller matching study after retrofitting propeller boss-cap-fin (PBCF)[J]. Ocean Engineering, 2023, 285: 115364. doi: 10.1016/j.oceaneng.2023.115364
[21]	KIM D, YIM J, SONG S, et al. Path-following control problem for maritime autonomous surface ships (MASS) in adverse weather conditions at low speeds[J]. Ocean Engineering, 2023, 287: 115860. doi: 10.1016/j.oceaneng.2023.115860
[22]	YASUKAWA H, HIRATA N, MATSUMOTO A, et al. Evaluations of wave-induced steady forces and turning motion of a full hull ship in waves[J]. Journal of Marine Science and Technology, 2019, 24(1): 1–15. doi: 10.1007/s00773-018-0537-3
[23]	MIEDEMA S A, LU Z H. The dynamic behavior of a diesel engine[C]//Proceedings of WEDA XXII Technical Conference & 34th Texas A&M Dredging Seminar. Denver, Colorado, USA, 2002. (查阅网上资料, 未找到本条文献出版者信息, 请确认)
[24]	中国船舶工业集团公司, 中国船舶重工集团公司, 中国造船工程学会. 船舶设计实用手册[M]. 3版. 北京: 国防工业出版社, 2013. China State Shipbuilding Corporation, China Shipbuilding Industry Corporation, China Shipbuilding. Practical handbook of ship design[M]. 3rd ed. Beijing: National Defense Industry Press, 2013 (in Chinese). (查阅网上资料, 未找到本条文献英文信息, 请确认)

施引文献

资源附件(0)

图(13) / 表(3)

计量

文章访问数: 84
HTML全文浏览量: 23
PDF下载量: 2
被引次数: 0

0. 引　言
1. 螺旋桨水动力模型建立
1.1 数值方法
1.2 计算域与网格划分
1.3 模型验证
1.4 数值计算结果分析
2. 船舶动力系统模型建立
2.1 目标船舶动力系统结构
2.2 主机平均值模型构建与验证
2.3 动力系统模型验证
3. 波浪影响下动力系统运行特性
3.1 波浪模型设置
3.2 船舶动力系统加速工况性能分析
4. 结　论

0. 引　言
1. 螺旋桨水动力模型建立
1.1 数值方法
1.2 计算域与网格划分
1.3 模型验证
1.4 数值计算结果分析
2. 船舶动力系统模型建立
2.1 目标船舶动力系统结构
2.2 主机平均值模型构建与验证
2.3 动力系统模型验证
3. 波浪影响下动力系统运行特性
3.1 波浪模型设置
3.2 船舶动力系统加速工况性能分析
4. 结　论

参考文献(24)

施引文献

资源附件(0)

基于多物理模型融合仿真的波浪对船舶动力系统加速性能的影响

通讯作者: 随从标

计量

出版历程

Influence of waves on the performance of ship power systems based on multi-physics fusion simulation model

0. 引 言

1. 螺旋桨水动力模型建立

1.1 数值方法

1.2 计算域与网格划分

1.3 模型验证

1.4 数值计算结果分析

2. 船舶动力系统模型建立

2.1 目标船舶动力系统结构

2.2 主机平均值模型构建与验证

2.3 动力系统模型验证

3. 波浪影响下动力系统运行特性

3.1 波浪模型设置

3.2 船舶动力系统加速工况性能分析

4. 结 论

计量

出版历程

目录

0. 引 言

1. 螺旋桨水动力模型建立

1.1 数值方法

1.2 计算域与网格划分

1.3 模型验证

1.4 数值计算结果分析

2. 船舶动力系统模型建立

2.1 目标船舶动力系统结构

2.2 主机平均值模型构建与验证

2.3 动力系统模型验证

3. 波浪影响下动力系统运行特性

3.1 波浪模型设置

3.2 船舶动力系统加速工况性能分析

4. 结 论

通讯作者:
随从标

0. 引　言

4. 结　论

0. 引　言

4. 结　论