Structural dynamic load prediction method based on long short-term memory network
-
摘要:目的
针对传统代理模型无法处理具有时间依赖性的动态过程和异构数据的问题,提出一种基于长短时记忆网络(LSTM)的动态载荷代理模型方法。
方法代理模型包含载荷特征编码和载荷响应解码2个模块。首先,通过载荷特征编码模块的LSTM对动态外载荷时间序列进行特征提取;然后,将外载荷时序特征与结构参数特征进行融合,由载荷解码模块的LSTM进一步进行特征提取并生成最终输出,从而综合考虑动态外载荷时间序列和结构参数一维特征的异构数据输入,预测结构内力响应时间历程;最后,在有限元仿真数据集上对模型进行精度评估,并与其他代理模型方法进行对比。
结果结果显示,该动态载荷代理模型的平均精度可达98%,高于其他对比方法,且计算速度相较于有限元方法更快。
结论所提方法可解决时序−非时序异构数据的代理模型问题,具有精度高、效率高的优点,在快速迭代计算场景下能够发挥较大作用。
Abstract:ObjectiveTo address the limitations of traditional surrogate models in handling time-dependent dynamic processes and heterogeneous data, this paper proposes a dynamic load surrogate model method based on a long short-term memory (LSTM) network.
MethodsThe surrogate model is comprised of two modules: the load feature encoder and load response decoder. First, the LSTM in the load feature encoder performs feature extraction on the time series of dynamic external loads. Next, the extracted load features are combined with the structural parameter features. The LSTM in the load decoder conducts further feature extraction and finally generates output while comprehensively considering the heterogeneous data input of the dynamic external load time series and one-dimensional structural parameter features in order to predict the time history of internal force responses. Finally, the model's accuracy is evaluated using a finite element simulation dataset and compared with other surrogate model methods.
ResultsThe results show that the average accuracy of the dynamic load surrogate model can reach 98%, which is higher than that of other methods, and its calculation speed is faster than that of the finite element method.
ConclusionsThe proposed method addresses the issue of heterogeneous data involving both time-series and non-time-series features, and offers advantages such as high accuracy and efficiency, making it effective for fast iterative computation tasks.
-
0. 引 言
在船舶、空天、建筑等诸多领域,通过结构优化获得良好的动力学或静力学特征并同时实现安全、可靠、经济等目标是非常有价值的。结构优化涉及到的影响因素众多,结构在不同受力情况和结构参数下的力学响应均需考虑在内,然后再通过设计准则、数学规划或其他合适的算法对参数进行优化调整。
对结构优化而言,工作载荷预测是影响其效果的重要因素。一方面,精准预测工作载荷是优化的基础,对载荷过高或过低的估计均会带来安全性或是性能上的缺失。在结构设计的不同阶段,通常采用实验方法或是以有限元为主的数值计算方法。这些方法的有效性已得到广泛验证,并能保证工作载荷预测的精确度。另一方面,载荷预测的效率决定了优化算法的实现成本。通常而言,需要通过大量的实验或计算获取数据来实现对目标函数的估计,且数据量越大,对目标函数的估计越准确,这就意味着需要对满足约束条件的所有参数取值进行遍历。在设计参数量较大时,维度灾难的存在将导致这种遍历需要进行上万次甚至更多。出于时间上的考虑,想通过实验进行如此大量的验证不太可能,而对于以有限元为主的数值计算方法来说,如此巨大的算例数量也难以实现。除了庞大的计算量和计算时间外,网格划分也带来了巨大的人力成本。这就使得这些方法无法在较短的开发周期内达到精准的结构优化效果。可见,一种高效、快速且准确的载荷预测方法对于结构优化而言意义重大。
代理模型是解决这一问题的高效替代方法,被越来越多地应用于结构优化领域[1-2]。在通过有限元计算或实验获取一定量的数据后,可以根据数据用黑箱数学模型近似模拟真实物理模型,从而描述参数与载荷之间的关系。在之后的参数遍历过程中,只需通过函数的计算就可以获得载荷值,从而显著降低遍历成本[3]。例如,罗文俊等[4]的研究表明,引入代理模型的结构优化方法可大幅降低计算成本,提高计算效率,这对于缩短产品开发周期而言非常有利。代理模型方法包括响应面法(response surface)[5]、克里金法(Kriging)[6]、径向基函数法(radial basis function,RBF)[7]以及各种机器学习(machine learning)方法。响应面法、克里金法和RBF法是较为经典的代理模型构建方法,而其中克里金法的应用最为广泛[8-12]。这些经典方法是通过对一些简单函数的线性组合来完成对复杂函数的近似,例如多项式、指数函数等,因此处理非线性和高维问题的能力略显不足。近年来,随着人工智能特别是机器学习方法的迅速发展,随机森林(random forest)、支持向量回归(support vector regression,SVR)以及人工神经网络(artificial neural networks)等机器学习方法被引入代理模型领域。机器学习具有强大的非线性拟合能力,这是其相对于传统代理模型方法的一个巨大优势。此外,机器学习的高维特征处理能力也强于传统方法,这使得机器学习方法在代理模型领域的适用性很高,基于决策树[13-14]和SVR[15-16]的代理模型均取得了一些研究成果。特别值得一提的是深度学习方法,通过模型结构的设计和模型容量的加大,深度学习模型具有强大的特征提取能力,不仅使代理模型的非线性能力更强,也使得端到端的代理模型成为可能,可以直接使用图像或时间序列作为输入输出[17-19]。
在载荷预测问题上,深度学习强大的特征提取能力和灵活的架构使得建立动态外载荷输入与结构载荷响应之间的代理模型成为可能,而受制于方法的局限性,传统的代理模型往往不能将外载荷和结构参数的异构数据作为代理模型的输入。由于外载荷为时间序列的二维结构,而结构参数为非时间序列的一维结构数据,故传统代理模型方法通常只针对其中一种类型的数据。因此,有部分[14]传统代理模型只针对静力学进行分析。然而,在实际情况下,静力学分析的适用范围有限,且无法为复杂的动态过程提供足够的载荷预测信息。另有部分代理模型[20-21]是针对动力学进行分析,能够处理动态载荷预测问题,但不能考虑结构参数对载荷响应的影响,无法满足结构优化的需要。
因此,利用深度学习端到端的学习能力,本文将对载荷预测代理模型的输入输出进行重新定义,构建一种基于长短时记忆网络(long short-term memory,LSTM)的动态载荷代理模型,以动态外载荷的时间序列数据和分析对象结构参数的非时序数据作为输入,预测结构内部多个截面的内力响应时间历程。该模型以编码器−解码器框架为基础,通过编码器对动态外载荷输入进行特征提取,通过解码器融合外载荷特征和结构参数,然后输出最终结果。在实验验证方面,通过有限元分析计算同一梁结构在不同结构参数和外载荷激励下不同截面的内力响应,并以计算结果作为数据集,训练代理模型并验证其精度。最后,将以结构参数相关性分析为例,将所构建的代理模型应用到大量算例的快速计算场景,以展示代理模型较高的计算效率。
1. 代理模型构建方法
1.1 问题描述
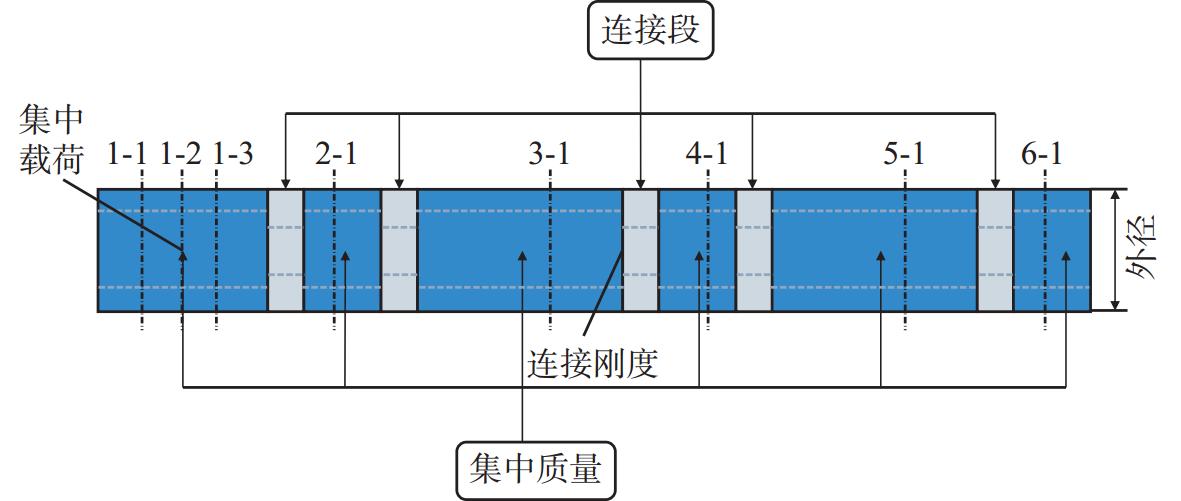
本文主要研究不同结构参数的梁模型在动态外载荷条件下的内力响应,研究对象如图1所示。该模型为一维空心梁模型,共有6段,每段梁之间通过连接段连接。梁和连接段虽材料属性不一样,但均为线弹性,其外径相同但厚度不同。为简化计算,将在梁的特定位置处赋予集中质量,而其他梁段则均无质量。
在最左端集中质量点处,该梁模型受到x方向和y方向的动态集中载荷Fx和Fy。在不同梁段分别选取截面,监测其内力响应时间历程。所选取的截面分别为左端梁段3个截面、其他梁段各1个截面,这是因为在左端受到集中载荷的梁段的内力响应更受关注。所监测的内力包括x方向轴力和y方向弯矩。这意味着,代理模型关注的输出共有16个不同的内力。
1.2 代理模型构建
假设梁模型的结构参数为P,受到的外载荷为L,内部各截面的内力响应为R,三者之间的关系为:
{\boldsymbol{R}} = f({\boldsymbol{P}},{\boldsymbol{L}}) (1) 代理模型使用数据的方法,以一个黑箱数学模型估计f建立近似关系 \hat{f} 来代替数值计算或实验方法的计算过程,从而显著减少计算时间。其关系式如下:
{\boldsymbol{R}} = \hat f({\boldsymbol{P}},{\boldsymbol{L}},{\boldsymbol{\theta }}) + {\boldsymbol{\varepsilon }} (2) 式中: \boldsymbol{\theta } 为代理模型参数; \boldsymbol{\varepsilon } 为误差。
代理模型是一种基于数据而非物理规律的方法,其参数需要通过已有数据估计获得,而这些已有数据可以通过数值计算或是实验获得。因此,代理模型并不能取代数值计算或实验,必须先通过这两者获取一部分数据完成对参数的估计后,才能在之后的迭代优化计算中起到加速的作用。
不同于传统代理模型,本文构建的代理模型将外载荷时间历程直接以时间序列二维数据的形式输入,通过一定的深度神经网络设计融合结构参数非时序一维输入,最终输出梁结构上多个截面的内力响应历程时间序列。外载荷输入包括给定位置外载荷沿x,y方向的分量Fx和Fy,结构参数输入包括梁模型梁段与连接段的连接刚度Kc、梁外径Rb、梁材料弹性模量Eb和连接段材料弹性模量Ec,输出参数包括各给定截面的轴力Fs和y方向弯矩Ms。
1.3 模型结构
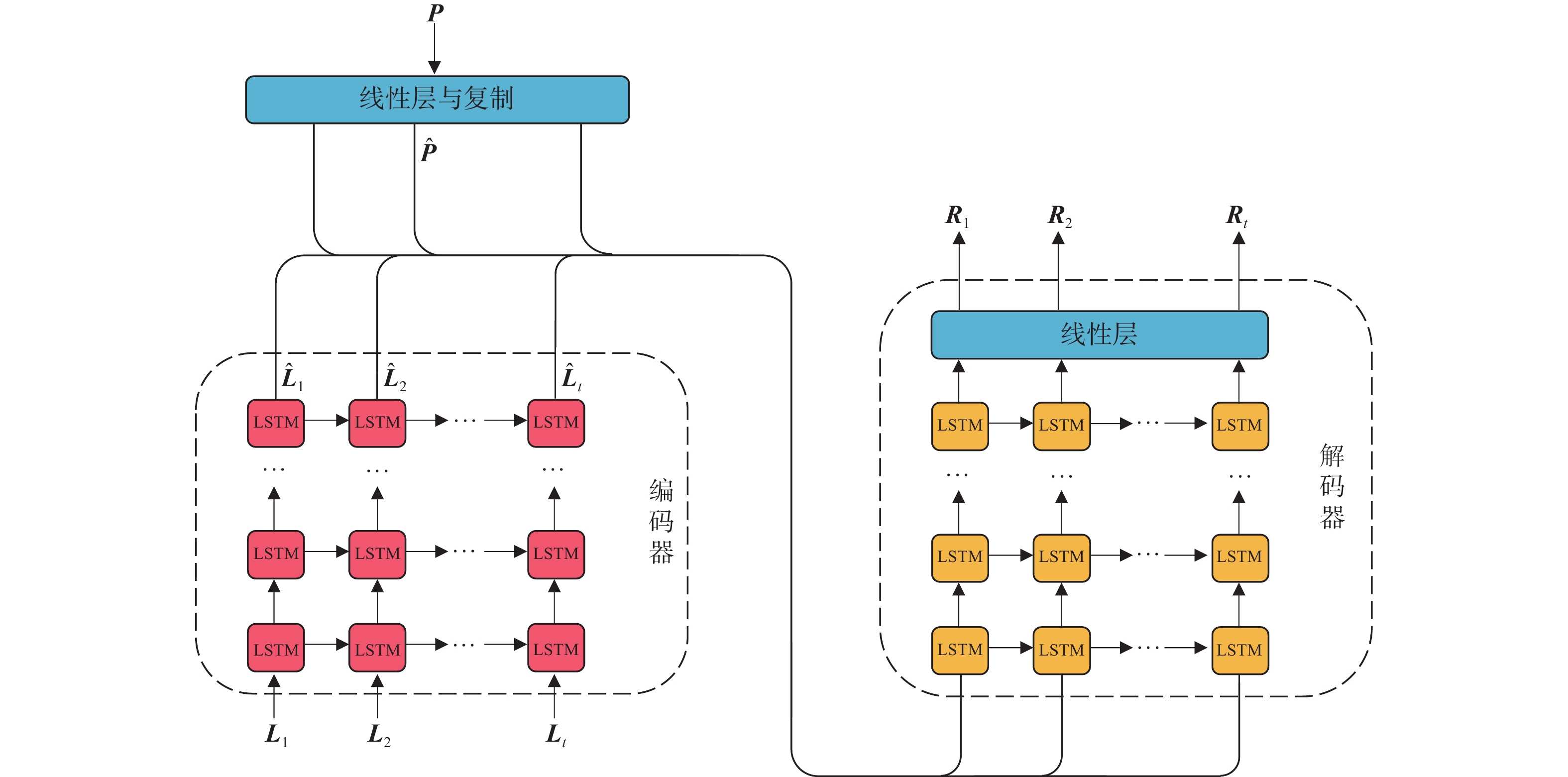
本文设计的代理模型深度网络主要采用编码−解码结构将时序外载荷历程和非时序结构参数融合。首先,对于外载荷,通过LSTM网络对时间序列的处理能力,对输入的外载荷时间历程进行编码以提取特征;而对于结构参数,则通过线性层提取其特征。在解码器中将结构参数特征复制升维,再将外载荷每个时间步的特征与结构参数特征融合,之后通过另一个LSTM网络解码器对融合特征进行进一步的回归,最终输出与外载荷时间步相对应的内力响应时间序列。该模型结构示意图如图2所示,其中\hat {\boldsymbol{L}} 为外载荷特征,\hat {\boldsymbol{P}} 为结构参数特征,下标t为时间步。
1.3.1 载荷特征编码
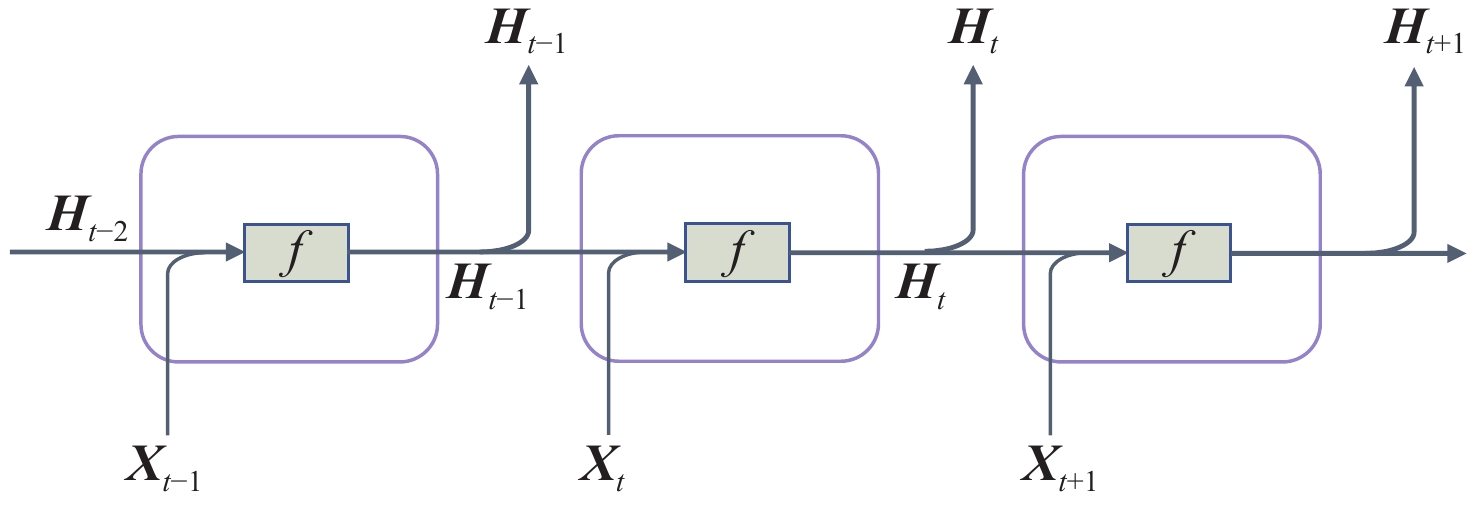
在涉及时间依赖性的动态载荷问题中,外载荷输入随时间变化,因此在代理模型中需以时间序列的形式表达,才能提取其隐藏于时间中的潜在模式。鉴此,将采用循环神经网络(recurrent neural network,RNN)类模型对载荷时间特征进行编码,RNN类模型的普遍结构如图3所示。图中,Xt为时间步t的输入,Ht为隐藏状态。值得一提的是,在动态结构载荷响应问题中,某一时刻载荷响应的值只由当前时间点及之前时间点决定,而RNN类模型包括很多沿时间方向连接排列的单元,每个单元接受当前时刻的输入和前一个时间点的隐藏状态并产生输出,其中隐藏状态包括前一个时间点及之前所有时间步单元提取的信息,这与载荷响应问题的特点非常契合。
具体地,针对动态载荷长序列的特点,载荷编码器选取LSTM网络。普通的RNN在处理长序列时存在梯度消失或爆炸的问题,导致性能不理想。为此,Hochreiter等[22]提出以LSTM作为解决方案,在RNN单元中增加3个门,即输入门、输出门和遗忘门,门选择性地传输包含在单元状态中的信息,解决了梯度消失和梯度爆炸的问题,使得LSTM在处理长序列问题上相比传统RNN更具优势。在载荷预测问题中,为了获得高精度的结果,离散的时间步长非常短,有时不足1 ms,这就导致短时间的仿真产生的时间序列也有成百上千的时间步,属于长序列的范畴,因此,比较适合采用LSTM进行处理。
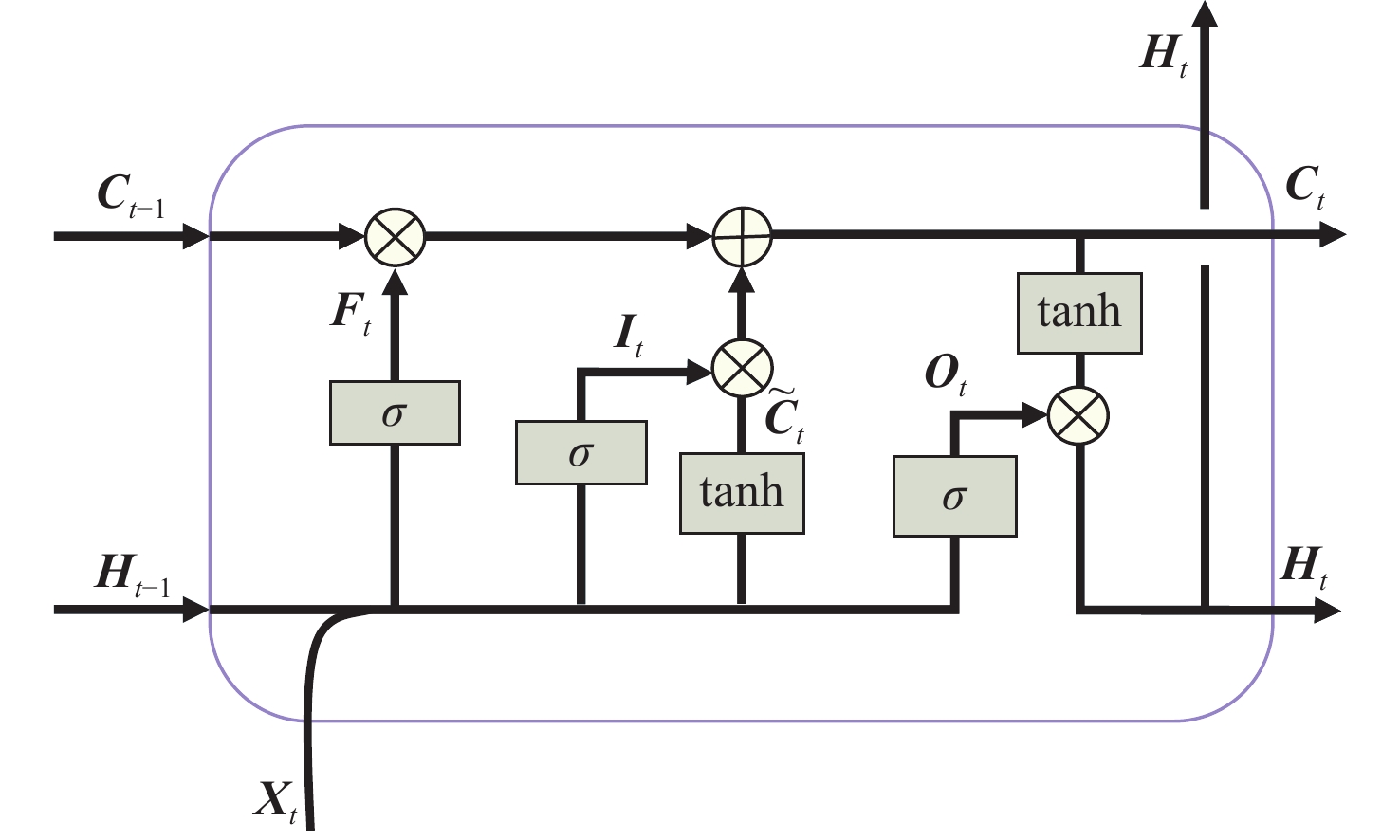
LSTM中单个记忆单元的结构如图4所示。图中,Ct表示单元状态,其值受3个 \sigma 函数的影响,从左到右,第1个 \sigma 函数是遗忘门,它决定在上一个时间步的单元状态中哪些信息将被丢弃;第2个 \sigma 函数是输入门,其将输入的新信息添加到单元状态;最后一个 \sigma 函数是输出门,选择哪些信息应该输出到隐藏状态Ht。LSTM单元可以表示如下:
\begin{split} & \;\;\;{\boldsymbol{I}}_{{t}}=\sigma ({\boldsymbol{X}}_{{t}}{\boldsymbol{W}}_{{t}}{xi}+{\boldsymbol{H}}_{{{t}}-1}{\boldsymbol{W}}_{hi}+{\boldsymbol{b}}_{i})\\& \;\;\;{\boldsymbol{F}}_{{t}}=\sigma ({\boldsymbol{X}}_{{t}}{\boldsymbol{W}}_{xf}+{\boldsymbol{H}}_{{{t}}-1}{\boldsymbol{W}}_{hf}+{\boldsymbol{b}}_{f})\\& \;\;{\boldsymbol{O}}_{{t}}=\sigma ({\boldsymbol{X}}_{{t}}{\boldsymbol{W}}_{xo}+{\boldsymbol{H}}_{{{t}}-1}{\boldsymbol{W}}_{ho}+{\boldsymbol{b}}_{o})\\& \tilde {\boldsymbol{C}}_{{t}}=\mathrm{tanh}({\boldsymbol{X}}_{{t}}{\boldsymbol{W}}_{xc}+{\boldsymbol{H}}_{{{t}}-1}{\boldsymbol{W}}_{hc}+{\boldsymbol{b}}_{c})\\& \;\;\;\;\;\;\;\;\;{\boldsymbol{C}}_{{t}}={\boldsymbol{F}}_{\rm{t}}\odot {\boldsymbol{C}}_{{{t}}-1}+{\boldsymbol{I}}_{{t}}\odot \tilde {\boldsymbol{C}}_t\\& \;\;\;\qquad{\boldsymbol{H}}_{{t}}={\boldsymbol{O}}_{{t}}\odot \mathrm{tanh}({\boldsymbol{C}}_{{t}}) \end{split} (3) 式中:It为输入门输出;Ft为遗忘门输出;Ot为输出门输出;\tilde {\boldsymbol{C}}_{{t}} 为候选单元状态;W为权重;b为偏差; \sigma 和tanh分别为sigmoid函数以及双曲正切函数;下标x,h,i,f,o,c分别表示该权重或偏置与Xt,Ht,It,Ft,Ot,\tilde {\boldsymbol{C}}_{\rm{t}} 有关。
LSTM编码网络可以提取时间序列的时间依赖性信息,完成对时间序列的特征提取,其表达式如下:
{\boldsymbol{\hat L}}_t = {\text{enc}}({\boldsymbol{L}}_{\text{1}},...,{\boldsymbol{L}}_t),\;\;\;t = 1,2,...,T (4) 式中,T为时间序列总长度。
1.3.2 载荷响应解码
编码器完成对动态外载荷的特征提取后,由解码器融合外载荷特征和结构参数特征,然后解码输出结构内部动态内力响应。在此之前,首先需对结构参数进行简单的特征提取。使用一个不带任何非线性激活函数的线性全连接层,目的是对特征维度进行变换,然后根据超参数搜索的结果选择将结构参数投影到更高维度以获取高维特征,或者将其压缩到更低维度以排除与输出相关性相对较低的参数,公式如下:
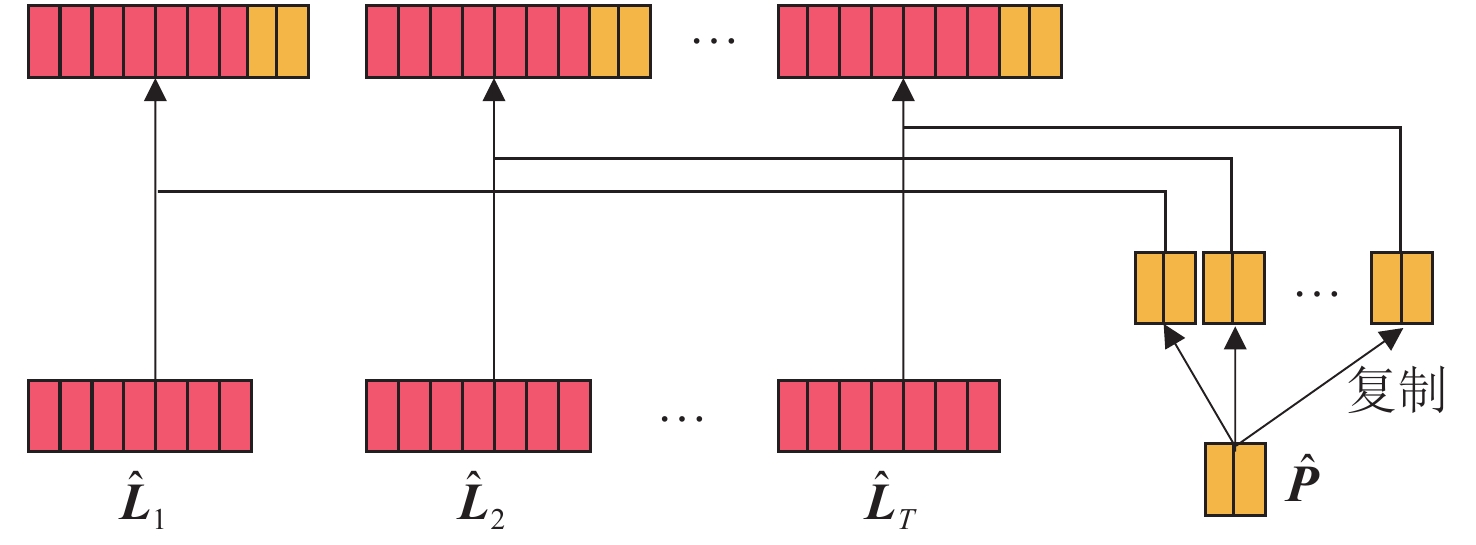
{\boldsymbol{\hat P}} = {\boldsymbol{W}}_{{x}}{\boldsymbol{P}} + {\boldsymbol{b}} (5) 经过线性层后,这些特征仍是一维数据,因此将其复制,复制次数与外载荷时间序列长度一致,随后将复制后的特征与外载荷特征进行组合,方法如图5所示。组合后的特征为二维数据,其长度等于外载荷时间序列长度,其特征维数等于结构参数特征数与外载荷特征数之和。
获得组合特征后,通过LSTM网络对其进行解码。该LSTM网络与编码器中的LSTM网络是相互独立的,这就意味着编码器和解码器的LSTM拥有不同的参数和超参数。在该LSTM网络后,使用一个线性全连接层,对LSTM网络的输出进行特征维度变换,输出8个截面共16个内力,避免LSTM网络的超参数受到输出维度的限制。
结构参数特征提取、复制和特征组合,以及组合特征解码共同构成解码器,可用下式表示:
{\boldsymbol{R}}_t = {\text{dec}}({\boldsymbol{P}} , {\boldsymbol{\hat L}}_1,...,{\boldsymbol{\hat L}}_t) (6) 1.4 评价指标
本文共使用2种指标对模型进行评价:均方误差E1和相对误差E2,其中均方误差是神经网络处理回归问题时最常用的指标,本文将其作为代理模型的损失函数用于模型参数更新,其公式为
E_1 = \frac{1}{{NTD}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^T {\sum\limits_{k = 1}^D {{{({y_{ijk}} - {{\hat y}_{ijk}})}^2}} } } (7) 式中: {y}_{ijk} 为真实值; {\hat{y}}_{ijk} 为模型输出值;N为样本数量;D为输出变量数。
为了更直观地表示代理模型对内力响应的预测精度,便于对代理模型进行评价,定义相对误差如下:
E_2 = \frac{1}{{NTD}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^T {\sum\limits_{k = 1}^D {\frac{{\left| {y_{ijk} - \hat y_{ijk}} \right|}}{{\mathop {\max }\limits_j \left| {y_{ijk}} \right|}}} } } (8) 之所以不逐项计算相对误差,而要分母在时间维度上取最大绝对值,这是因为输出存在一些值为0的时间点,会影响相对误差的计算。不同方法的评价和方法间的对比将主要基于此定义下的相对误差来进行。
2. 数值实验
对于本文构建的动态载荷代理模型,在通过有限元计算获得的仿真数据集上对其进行验证。数值实验的主要内容包括数据集构造与预处理、模型训练与验证、结构参数相关性分析案例。下面,将分步对数值实验进行介绍。
2.1 数据集构造与预处理
通过ABAQUS软件进行有限元分析,本文构造了包含10 000个算例的仿真数据集。研究对象模型前文已介绍。在仿真数据集中,不同算例的外载荷和结构参数不同。对于外载荷,根据实际情况,假设其以集中载荷的形式施加在梁最左端的集中质量处。为尽量提高载荷复杂度,模拟梁段在工作过程中随机的受力情况,施加的载荷为随机载荷,其功率谱密度在20~200 Hz之间为常数,这覆盖了梁模型的前4阶模态。在其他频段,功率谱密度为0。每个算例均随机生成x方向和y方向的随机载荷,这就意味着每个算例、每个方向的载荷分量均不同。
对于结构参数,为确保参数分布的均匀性,本文采用拉丁超立方方法在参数空间中随机采样
10000 次,每个算例采用一组结构参数。改变的结构参数包括梁与连接段的连接刚度Kc、梁外径Rb、梁的弹性模量Eb和连接段材料的弹性模量Ec。不同参数的基准值和变化范围如表1所示。表 1 结构参数的取值范围Table 1. Range of structural parameters输入参数 连接刚度
Kc /(N∙m−1)梁外径
Rb/m梁的弹性
模量Eb /Pa连接段材料
弹性模量Ec /Pa基准 1 \times 107 0.325 7.10 \times 1010 2.10 \times 1011 下限 1 \times 107 0.309 7.10 \times 1010 2.10 \times 1011 上限 2 \times 107 0.341 7.81 \times 1010 2.31 \times 1011 对于每个算例,施加时长为0.2 s的随机载荷,结构参数按照拉丁超立方采样结果设置,有限元仿真时输入载荷的时间间隔为0.05 ms。仿真时间设置为0.2 s,仿真步长为0.5 ms,输出时间间隔为0.001 s。在这样的设置下,载荷输入和输出的采样频率能够保证不会丢失随机载荷和载荷响应在20~200 Hz频段的信息。
在所有算例完成计算后,对算例进行数据处理。首先,对外载荷输入进行降采样。出于仿真精度的要求,计算时,将外载荷输入的采样频率设置为输出频率的20倍。这就造成外载荷输入的时间序列长度极长,使得代理模型的计算量巨大。考虑到输出的采样频率已达到随机载荷最高频率的5倍,不会丢失外载荷及载荷响应的高频信息,因此对代理模型的外载荷输入进行20倍降采样,使其采样频率与输出的采样频率相同。经降采样后的外载荷时序长度将与内力响应输出一致,均为200,这将使得代理模型的结构设计更为简单。
经降采样之后,针对外载荷、结构参数与内力响应进行数据标准化,用以加快神经网络训练速度,提高训练精度。标准化的公式为:
\hat X = (X - {X_{\rm{mean}}} )/{X_{\rm{std}}} (9) 式中:X为单一特征变量; {X_{\rm{mean}}} 为单一特征变量的平均值; {X_{\rm{std}}} 为标准差。标准化将所有特征映射至平均值为0、标准差为1的分布,使每个特征都有相近的取值范围。对于结构参数,在样本间计算平均值和标准差以进行标准化,而对于外载荷和内力响应的时间序列而言,则在样本和时间维度统一进行标准化。
完成数据预处理后,按60%,20%,20%的比例将数据集划分为训练集、验证集和测试集,即训练集包含6 000个样本,验证集和测试集各包含2 000个样本。由于每个算例的载荷是随机生成的,结构参数各不相同,因此这3个数据集中的数据并不重复。
2.2 模型训练与验证
经过模型在训练集上的训练,以及根据验证集进行的超参数选取,确定采用的超参数如下:编码LSTM的隐藏单元数denc = 8,层数nenc = 2;结构参数投影线性层的隐藏单元数dpram = 3,即对结构参数进行了降维;解码LSTM的隐藏单元数ddec = 32,层数ndec = 2;最后一个线性层的隐藏单元数dlin = 16。使用Adam对模型进行训练,批量数B = 128,学习率 \eta = 0.005,一阶矩估计的指数衰减率β1 = 0.9,二阶矩估计的指数衰减率β2 = 0.999,训练轮次nepoch为200轮。表2列出了所有超参数的数值。
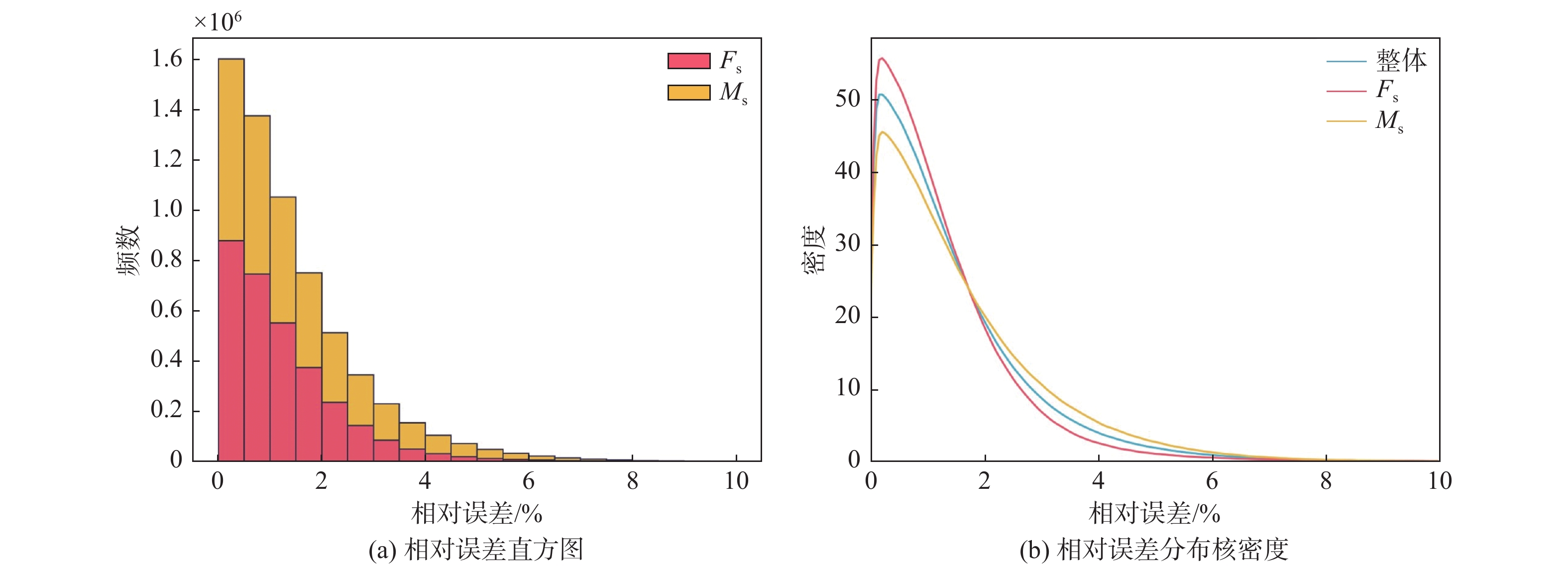
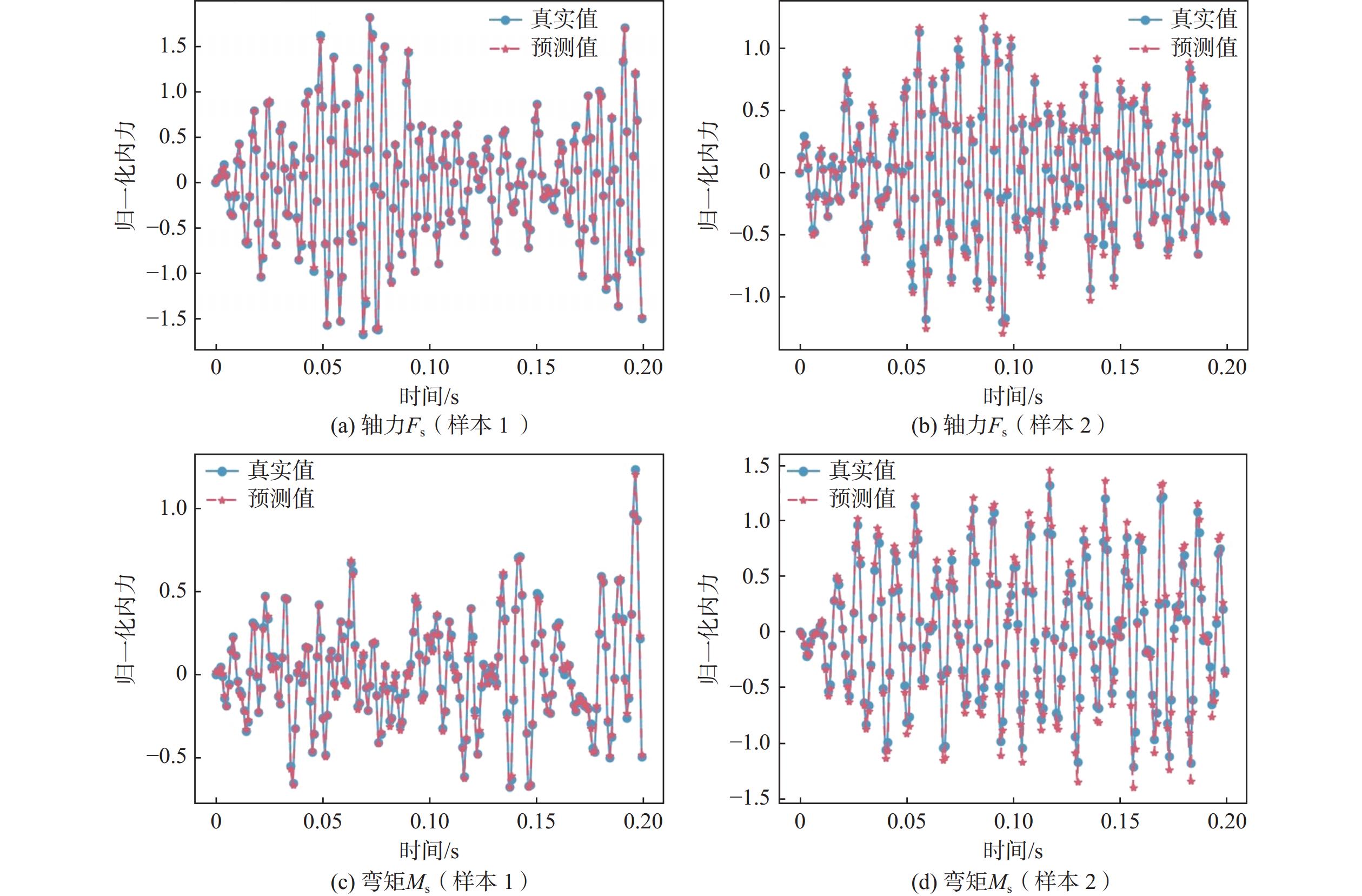
表 2 超参数设置Table 2. Configuration of hyperparameters超参数 数值 超参数 数值 nenc 2 denc 8 ndec 2 ddec 32 dpram 3 dlin 16 B 128 \eta 0.005 β1 0.9 β2 0.999 nepoch 200 表3展示了训练后的模型在测试集数据上预测不同内力响应时的相对误差。该模型的平均相对误差为1.5%。对于x方向轴力Fs和y方向弯矩Ms,相对误差的分布如图6所示。结果显示,Fs的平均相对误差较小,为1.3%,相对误差较小的区域概率密度较大,而Ms的平均相对误差较大,为1.6%。图7以测试集误差最小的样本1和误差最大的样本2为例,直观地展示了代理模型对1-2截面轴力Fs和弯矩Ms的预测结果与真实值的对比。
表 3 代理模型相对误差Table 3. Relative error of surrogate model参数 不同截面内力响应相对误差/% 1-1 1-2 1-3 2-1 3-1 4-1 5-1 6-1 轴力Fs 1.2 1.4 1.2 1.2 0.9 1.2 1.6 1.7 弯矩Ms 1.7 2.0 1.7 1.7 1.5 1.3 1.4 1.6 为了验证本文所提模型对动态载荷的预测效果,与应用广泛的多层感知器和随机森林进行了精度比较。为了验证将结构参数融合于动态载荷代理模型的有效性,还构建了无结构参数输入的LSTM模型,以及其他文献中的动态载荷代理模型,包括文献[21]中的deep RNN和文献[22]中的ED-CRNN,并进行了对比。对比方法的结构如下:
1) 对于多层感知器,由于其只能接收一维输入并进行一维输出,因此将外载荷二维时间序列展开成一维特征并与结构参数合并作为输入,将内力响应时间序列展开为一维作为输出。除输入层和输出层外,该模型还包含3个隐藏层,每个隐藏层的单元为512个。其训练参数与本文所提模型一致。
2) 对于随机森林,由于其与多层感知器一样只能接收一维输入输出,因此其输入输出与多层感知器一致。结构上,其最大深度为10,集成决策树为100个。
3) 对于LSTM,仅以外载荷作为输入,以内力响应作为输出。结构上,相比本文所提模型,去掉了针对结构参数的线性层与复制,并且在编码器和解码器之间没有特征组合的步骤。其他参数均与本文所提模型一致。
4) 对于deep RNN[21]和ED-CRNN[22],由于其只适用于时间序列输入输出,无法考虑结构参数输入,因此输入输出与LSTM一致。出于对超参数寻优结果和控制模型参数与本文基本一致的考虑,这2种模型的隐藏单元数均设置为32,其他参数的设置与原文献中相同。
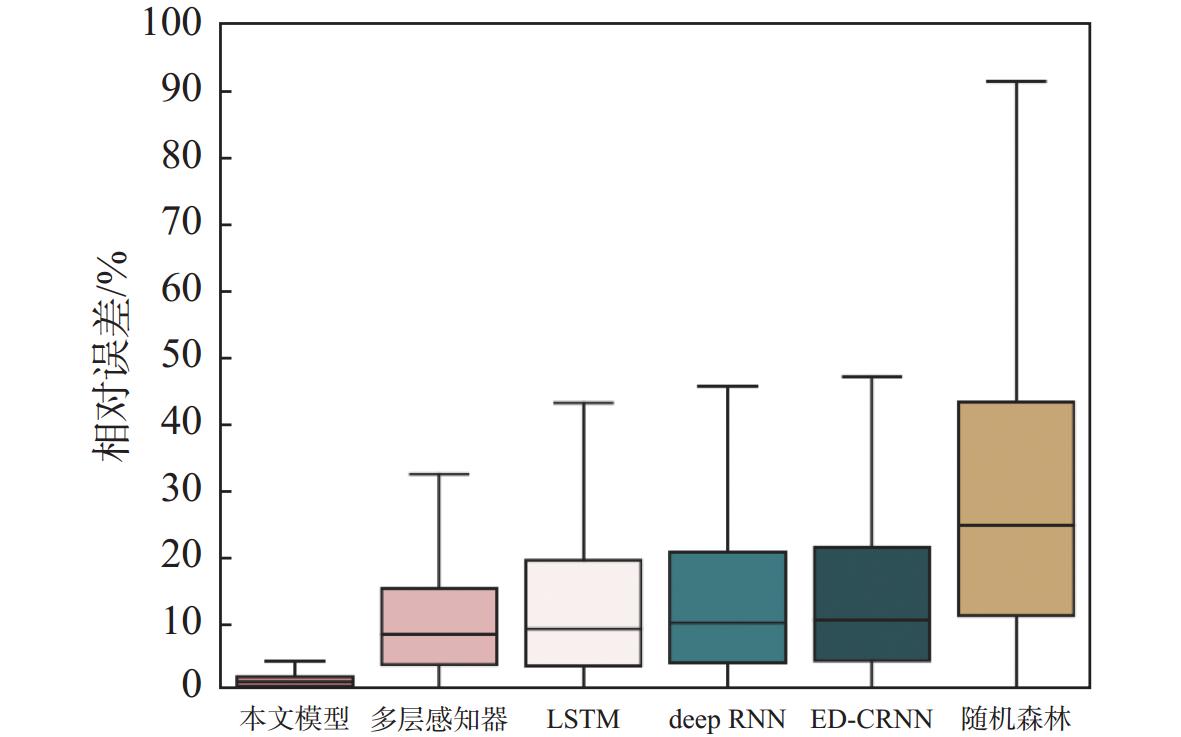
每种方法在测试集上的误差分布如图8所示。结果表明,本文所提方法相比另外5种方法在准确性和稳定性上均有较大的优势。
首先,对于多层感知器和随机森林,由于没有针对动态载荷问题所涉及的时序、非时序混合输入进行特别的设计,因此,结构参数与外载荷共同结合为一维特征,在这种设计下,外载荷由于时序长度较大,所占的特征数远远多于结构参数,导致结构参数特征在模型中的重要性很难被捕获。此外,从模型结构方面分析,多层感知器对所有输入做了全连接,外载荷时间序列的每个时间步都有对应的拟合参数,导致网络整体参数量过大,出现了比较严重的过拟合现象,其在训练集上的相对误差能达到5%,但在测试集上的相对误差却只有10%左右。随机森林则是其每个单独的决策树都对输入参数进行了特征选择,因此外载荷的时序信息会有所丢失,无法给出精确的预测结果。
其次,对于LSTM,deep RNN和ED-CRNN,尽管其模型能够较好地提取动态外载荷的时序特征,但因为缺少结构参数的信息,模型的内力响应无法被确定,因此精度不高。这也说明将外载荷与结构参数的异构数据融合是有必要的,本文提出的融合模型有效。
相比其他方法,本文提出的模型是使用LSTM编码网络处理外载荷时序输入进行特征提取,然后再将其与经过线性变化和复制的结构参数进行结合。这种方式使得2种输入的重要性在模型中是相似的。此外,同一个LSTM层中每个单元的参数是共享的,这就意味着对于每个时间步的输入,LSTM单元都以相同的方式进行处理,这种先验知识启发的结构设计使得其参数量小于多层感知器。在这2个因素的共同作用下,模型能对本文所提问题进行较高精度的预测。
2.3 应用案例——结构参数相关性分析
相关性分析是代理模型的优势应用场景之一。在相关性分析中,需改变参数并进行大量算例的计算,然后判断参数对结果的影响。对有限元方法而言,计算大量不同的算例非常耗时,因此可以通过引入代理模型来提高计算效率。本节将运用本文构建的代理模型进行结构参数相关性分析,以展示其快速计算能力。首先,固定外载荷、改变结构参数,然后利用代理模型对
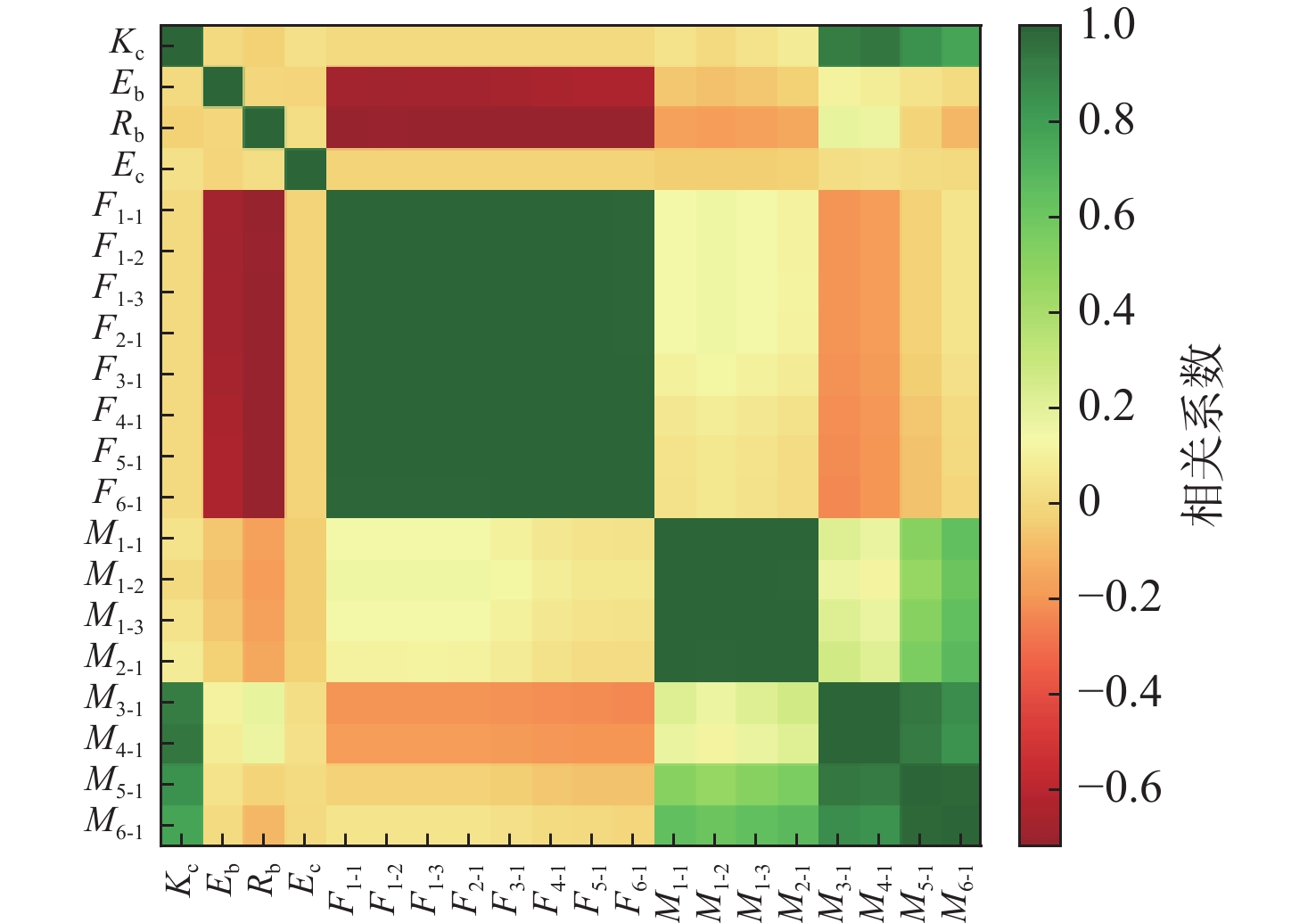
2000 个算例进行计算,最后,根据计算结果画出了如图9所示的皮尔逊相关系数矩阵。图中,F为轴力,M为弯矩,下标为截面编号。每2个变量X,Y之间的皮尔逊相关系数计算公式如下:{{{corrcoef}}} (X,Y) = \frac{{{{{cov}}} (X,Y)}}{{\sqrt {{{{var}}} (X){{{var}}} (Y)} }} (10) 式中:cov()为协方差;var()为方差。皮尔逊相关系数的绝对值越接近于1,说明两个变量之间的相关性越强,而正、负号则代表正相关或是负相关。值得一提的是,皮尔逊相关系数只能在2个一维变量之间计算,因此针对内力响应这一时序变量,本文将采用其在时间维度上的标准差予以替代。由于所有内力响应在时间维度的均值都为0,故标准差的大小即代表了内力响应的强度。
通过相关性矩阵可以得出,不同结构参数之间相互独立,这也表明了算例生成的正确性、截面轴力Fs与梁的弹性模量Eb和外径Rb具有较强的负相关性、截面弯矩Ms与连接刚度Kc具有较强的正相关性,以及连接段弹性模量与内力响应没有明显的相关性。这主要是因为结构参数的改变影响了梁模型的固有频率。由于所施加的外载荷是固定的,并不具备功率谱密度为常数的统计特性,因此其在特定的频率下幅值较高,当梁模型的固有频率与这些频率接近时,容易引起这些频率上的共振,从而使得轴力和弯矩的时间尺度标准差增大。在本案例的外载荷条件下,相关性分析结果表明,梁的弹性模量Eb和外径Rb越小、连接刚度Kc越大,越容易引发共振。
另外,值得注意的是,代理模型超参数选择结果表明,对结构参数进行特征提取的线性层只需提取出3个特征,就能给出较好的预测,这与相关性分析的结果是一致的,也即代理模型在结构参数线性映射时将连接段弹性模量这一无关参数过滤,完成了信息的压缩。
在NVIDIA GeForce RTX
3070 8GB上,代理模型计算2 000个算例的时间为2.0 ms,远少于有限元计算的时间,这充分体现了代理模型相对于传统数值计算方法的优势,即用极短的时间满足快速迭代计算的需求,这在结构优化、敏感性分析、相关性分析等场景有着较强的应用潜力。需要说明的是,本节相关性分析的结果仅适用于所选定的外载荷条件,因此在力学上的普适性较弱,仅能作为应用案例用于验证代理模型在快速迭代计算上的效率优势。
3. 结 论
本文基于深度学习方法构建了一种动态载荷代理模型,该模型利用编码器−解码器结构和LSTM网络,通过融合动态外载荷时序输入和结构参数非时序输入,较好地预测了梁结构多个截面的内力响应时间历程。该模型在由10 000个样本构成的有限元仿真数据集上进行了精度评估、方法对比和相关性计算,主要得到如下结论:
1) 本文所提动态载荷代理模型拥有端到端的建模能力,能同时接收外载荷时序输入和结构参数非时序输入,并以时间序列的方式预测内力响应时间历程,可为载荷预测计算提供更多信息。
2) 所提的动态载荷代理模型在测试集上能达到较高的精度,对于所有截面内力响应其平均预测精度可达98%,整体平均相对误差为1.5%,高于其他代理模型方法,体现了该代理模型在处理动态载荷问题和异构数据上的优势。
3) 该代理模型可以用于替代有限元方法进行大量算例的快速计算。结构参数相关性分析案例表明,该模型的计算速度和有限元方法相比更快,能够快速计算大量不同参数条件的算例,并给出载荷预测结果,这对于需要快速迭代计算的应用场景有着重大意义。
-
表 1 结构参数的取值范围
Table 1 Range of structural parameters
输入参数 连接刚度
Kc /(N∙m−1)梁外径
Rb/m梁的弹性
模量Eb /Pa连接段材料
弹性模量Ec /Pa基准 1 \times 107 0.325 7.10 \times 1010 2.10 \times 1011 下限 1 \times 107 0.309 7.10 \times 1010 2.10 \times 1011 上限 2 \times 107 0.341 7.81 \times 1010 2.31 \times 1011 表 2 超参数设置
Table 2 Configuration of hyperparameters
超参数 数值 超参数 数值 nenc 2 denc 8 ndec 2 ddec 32 dpram 3 dlin 16 B 128 \eta 0.005 β1 0.9 β2 0.999 nepoch 200 表 3 代理模型相对误差
Table 3 Relative error of surrogate model
参数 不同截面内力响应相对误差/% 1-1 1-2 1-3 2-1 3-1 4-1 5-1 6-1 轴力Fs 1.2 1.4 1.2 1.2 0.9 1.2 1.6 1.7 弯矩Ms 1.7 2.0 1.7 1.7 1.5 1.3 1.4 1.6 -
[1] 刘婧, 王德禹. 基于SMOTE算法和动态代理模型的船舶结构可靠性优化[J]. 中国舰船研究, 2020, 15(5): 114–123. doi: 10.19693/j.issn.1673-3185.01657 LIU J, WANG D Y. Reliability-based design optimization of ship structure using SMOTE algorithm and dynamic surrogate model[J]. Chinese Journal of Ship Research, 2020, 15(5): 114–123 (in Chinese). doi: 10.19693/j.issn.1673-3185.01657
[2] 韩忠华, 许晨舟, 乔建领, 等. 基于代理模型的高效全局气动优化设计方法研究进展[J]. 航空学报, 2020, 41(5): 623344. HAN Z H, XU C Z, QIAO J L, et al. Recent progress of efficient global aerodynamic shape optimization using surrogate-based approach[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(5): 623344 (in Chinese).
[3] KUDELA J, MATOUSEK R. Recent advances and applications of surrogate models for finite element method computations: a review[J]. Soft Computing, 2022, 26(24): 13709–13733. doi: 10.1007/s00500-022-07362-8
[4] 罗文俊, 王德禹. 基于兴趣子域动态代理模型的船舶结构可靠性优化[J]. 中国舰船研究, 2021, 16(4): 96–107. doi: 10.19693/j.issn.1673-3185.02043 LUO W J, WANG D Y. Reliability-based optimization of ship structure based on interest subdomain dynamic surrogate model[J]. Chinese Journal of Ship Research, 2021, 16(4): 96–107 (in both Chinese and English). doi: 10.19693/j.issn.1673-3185.02043
[5] FREENY A. Empirical model building and response surfaces[J]. Technometrics, 1987, 30(2): 229–231.
[6] KRIGE D G. A statistical approach to some basic mine valuation problems on the Witwatersrand[J]. Journal of the South African Institute of Mining and Metallurgy, 1951, 52(6): 201–203.
[7] BROOMHEAD D S, LOWE D. Multivariable functional interpolation and adaptive networks[J]. Complex Systems, 1988, 2(3): 321–355.
[8] FAN X X, WANG P F, HAO F F. Reliability-based design optimization of crane bridges using Kriging-based surrogate models[J]. Structural and Multidisciplinary Optimization, 2019, 59(3): 993–1005. doi: 10.1007/s00158-018-2183-0
[9] CHU L, SHI J J, DE CURSI E S. Kriging surrogate model for resonance frequency analysis of dental implants by a Latin hypercube-based finite element method[J]. Applied Bionics and Biomechanics, 2019, 2019: 3768695.
[10] HASSAN A K S O, ETMAN A S, SOLIMAN E A. Optimization of a novel Nano antenna with two radiation modes using Kriging surrogate models[J]. IEEE Photonics Journal, 2018, 10(4): 4800807.
[11] HAERI A, FADAEE M J. Efficient reliability analysis of laminated composites using advanced Kriging surrogate model[J]. Composite Structures, 2016, 149: 26–32. doi: 10.1016/j.compstruct.2016.04.013
[12] SHI J J, CHU L, BRAUN R. A Kriging surrogate model for uncertainty analysis of graphene based on a finite element method[J]. International Journal of Molecular Sciences, 2019, 20(9): 2355. doi: 10.3390/ijms20092355
[13] LADICKÝ L, JEONG S, SOLENTHALER B, et al. Data-driven fluid simulations using regression forests[J]. ACM Transactions on Graphics, 2015, 34(6): 199.
[14] 李海泉, 陈小前, 左林玄, 等. 基于随机森林的飞行载荷代理模型分析方法[J]. 航空学报, 2022, 43(3): 225640. doi: 10.7527/j.issn.1000-6893.2022.3.hkxb202203025 LI H Q, CHEN X Q, ZUO L X, et al. Surrogate model for flight load analysis based on random forest[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(3): 225640 (in Chinese). doi: 10.7527/j.issn.1000-6893.2022.3.hkxb202203025
[15] WANG Q, QIAN W Q, HE K F. Unsteady aerodynamic modeling at high angles of attack using support vector machines[J]. Chinese Journal of Aeronautics, 2015, 28(3): 659–668. doi: 10.1016/j.cja.2015.03.010
[16] AL KAJBAF A, BENSI M. Application of surrogate models in estimation of storm surge: a comparative assessment[J]. Applied Soft Computing, 2020, 91: 106184. doi: 10.1016/j.asoc.2020.106184
[17] BAI T, TAHMASEBI P. Characterization of groundwater contamination: a transformer-based deep learning model[J]. Advances in Water Resources, 2022, 164: 104217. doi: 10.1016/j.advwatres.2022.104217
[18] ZHAO X Y, GONG Z Q, ZHANG J, et al. A surrogate model with data augmentation and deep transfer learning for temperature field prediction of heat source layout[J]. Structural and Multidisciplinary Optimization, 2021, 64(4): 2287–2306. doi: 10.1007/s00158-021-02983-3
[19] SHIBATA R, OHIRA M, MA Z W. A novel convolutional-autoencoder based surrogate model for fast S-parameter calculation of planar BPFs[C]//2022 IEEE/MTT-S International Microwave Symposium - IMS 2022. Denver: IEEE, 2022: 498-501.
[20] ZHOU J M, DONG L L, GUAN W, et al. Impact load identification of nonlinear structures using deep recurrent neural network[J]. Mechanical Systems and Signal Processing, 2019, 133: 106292. doi: 10.1016/j.ymssp.2019.106292
[21] CHEN T, GUO L, DUAN A D Z, et al. A feature learning-based method for impact load reconstruction and localization of the plate-rib assembled structure[J]. Structural Health Monitoring, 2022, 21(4): 1590–1607. doi: 10.1177/14759217211038065
[22] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735–1780. doi: 10.1162/neco.1997.9.8.1735



 下载:
下载: